Il Carnevale della matematica mi offre l’occasione per scrivere un nuovo articolo, senza aver bisogno di cercare un tema. Per questo mese di febbraio, poi, il tema è stato proposto dai Rudi con grande anticipo e questo mi ha permesso di pensarci a lungo e di raccogliere spunti in giro per il web. Dopo una prima googlata, che mi ha portato solo verso la classificazione dei punti di discontinuità, ho scovato un articolo di carattere più divulgativo, pubblicato sul blog Math is in the air nel 2017, scritto da Pierandrea Vergallo e intitolato La continuità: il senso delle cose matematiche. A partire da Federigo Enriques e zigzagando tra le definizioni dell’analisi, Vergallo approda al determinismo e al caos: la continuità è presentata come una stabilità, una ripetitività nella routine, come una goccia che cade in uno stagno generando onde concentriche (e così ho capito perché la prima immagine dell’articolo era quella di una goccia d’acqua). A me sono venute in mente quelle definizioni della fisica che definiscono una regolarità come fosse un’immobilità, penso ad esempio alla definizione di onda stazionaria, che rimanda all’immagine di una regolarità immobile, eppure in movimento, come il flusso laminare stazionario, quando capita di imbattersi nelle fontane dei paesi di montagna.

È confortante scoprire, nella lettura, l’associazione tra la discontinuità e la catastrofe: «Il legame è così stretto tra l’idea di catastrofe e quella di discontinuità che esiste una teoria matematica nota con il nome di Teoria delle singolarità o, appunto, teoria delle catastrofi». E una catastrofe è «un fenomeno geofisico imprevedibile e che crea una dissonanza tra il prima e il dopo». Questo mi ha rimandato ad una recente lettura che ha scosso un po’ le mie convinzioni, Il cigno nero di Nassim Nicholas Taleb, che, con la sua (sconcertante e rivoluzionaria) teoria sottolinea non solo l’imprevedibilità di certi eventi, ma anche la nostra difficoltà psicologica nell’accettare l’incertezza. Da un certo punto di vista, è stato confortante approdare alla conclusione dell’articolo di Vergallo e rendersi conto che anche le mie riflessioni durante la lettura del testo di Taleb erano andate nella stessa direzione: «La matematica, in questo caso, sembra la strada più serena, quella più evidente. […] Forse siamo fatti, parafrasando un famosissimo poeta inglese, della stessa sostanza dei tanto odiati numeri.»

Confortante.

Sconcertante.

Terrificante (per qualcuno!)

La nostra mente cerca in continuazione regolarità, ripetitività, abitudine, per riuscire in qualche modo a riposare. La ripetitività, che a certi livelli può essere considerata alienante (basti pensare alle catene di montaggio), nella vita di tutti i giorni può avere una sua serenità. Forse parlo (scrivo!) in questo modo perché sono particolarmente restia ai cambiamenti e a tutte quelle discontinuità inevitabili che caratterizzano la vita di chiunque e, per quanto mi renda conto che certi terremoti scuotono, ma regalano anche nuovi inizi, anelo alla monotonia. Perché quando si crea una discontinuità, non sai mai dove potrà portarti…

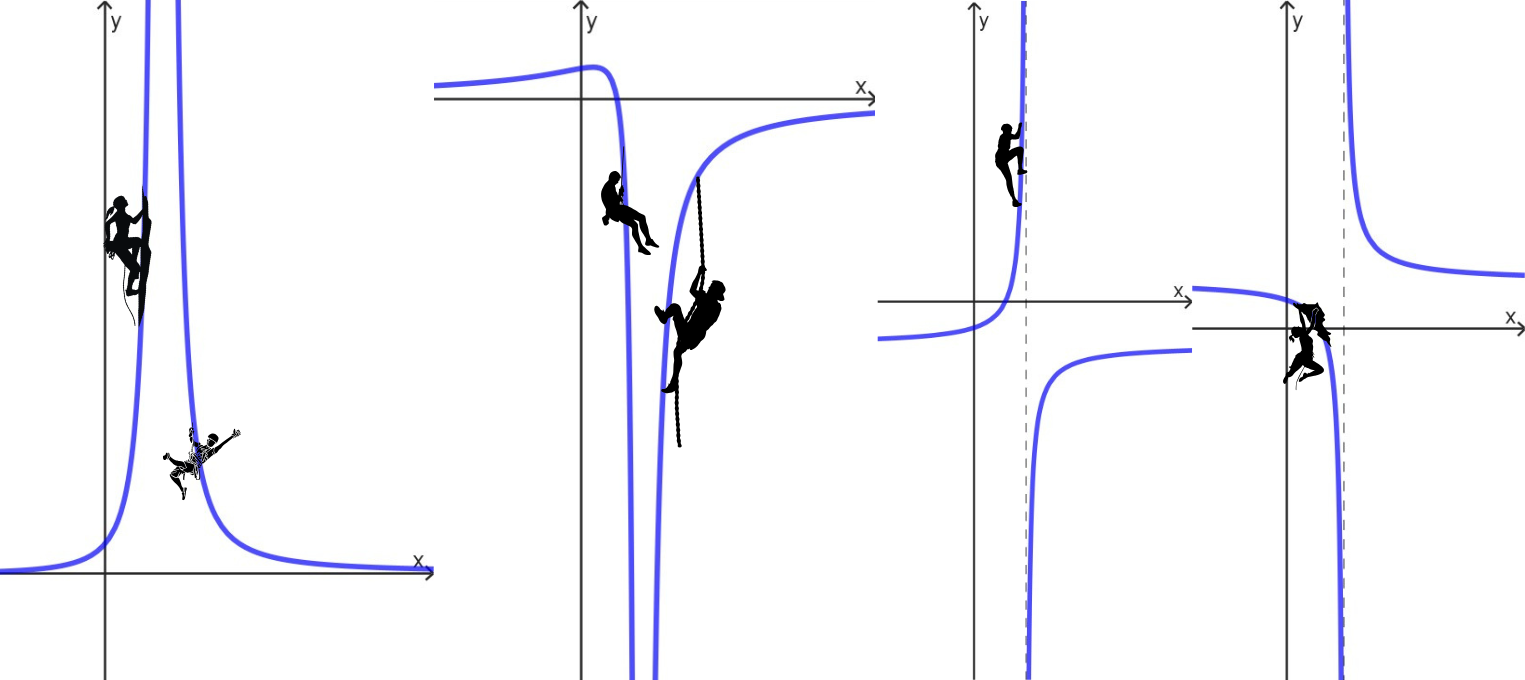
A volte è una breve interruzione, come un piccolo inciampo, l’assenza di un punto di appoggio, che però ti permette di procedere come se niente fosse successo e, guardandoti indietro, vedi solo un cammino continuo. Altre volte si tratta di discontinuità fatte da salti, gradini che ti trovi a superare in salita o in discesa.

Ma le discontinuità peggiori sono quelle di cui non ti accorgi finché è troppo tardi, un po’ come quei cigni neri così imprevedibili di cui parla Nassim Nicholas Taleb. In matematica, vengono chiamate discontinuità di seconda specie: «Si dice che in un punto una funzione f ha una discontinuità di II specie se in tale punto almeno uno dei due limiti destro o sinistro di f è infinito oppure non esiste.» Sei impegnato con una salita e, all’improvviso, vieni sbalzato su uno scivolo. Oppure stai faticando in discesa, cercando di non procedere troppo velocemente e, dal nulla, ti trovi ad arrancare in salita. O stai salendo (scendendo) e continui a salire (scendere) ma stai godendo di un panorama completamente diverso. Ma potrebbe anche capitare che tu stia camminando tranquillamente e, all’improvviso, ti si apra un baratro o che dallo scivolamento verso il basso, tu ti ritrovi a camminare in una strada di campagna, o… quanti casi diversi! E la matematica, sensazionale, raggruppa tutto sotto l’ombrello della discontinuità di seconda specie.

Con il suo linguaggio, la matematica ci offre metafore davvero illuminanti, e i suoi grafici ci aiutano a descrivere la realtà. Penso a quella studentessa che stava affrontando per la prima volta il prodotto tra monomi e, dopo aver visto un paio di esempi con prodotti tra monomi simili, reagì sconcertata di fronte a monomi non simili moltiplicati tra loro esclamando: «Questo non si può fare!» (ed ecco generata una misconcezione, solo per aver scelto gli esempi sbagliati!) Oppure penso agli studenti che, di fronte a un esercizio sulla diffrazione, abituati a disegni sempre uguali con superfici di contatto tra i fluidi orizzontali, abituati a disegnare una normale verticale, ne hanno disegnata una verticale anche se la linea di contatto era obliqua. Ognuno di noi, nella matematica a scuola (ma soprattutto nella vita) applica, più o meno consapevolmente, degli schemi, cerca una regolarità per non doversi mettere in gioco o per non faticare.

In famiglia, detengo il primato di quella più restia al cambiamento e ogni volta che cambio un dispositivo (o un’auto) o che devo modificare un’abitudine per qualche ragione, mio marito si prepara all’onda d’urto dei miei brontolii. Immaginate, quindi, il suo coraggio quando mi ha proposto di cambiare la struttura del sito (la terza volta dall’agosto del 2006). Nuova struttura significa nuove abitudini, nuovi modi di pubblicare i contenuti, rinuncia a dettagli che mi parevano importanti e irrinunciabili e che, invece, non erano così funzionali (ma questo lo scopro solo quando vengo obbligata a cambiare). Ogni volta che c’è stato un cambio grafico e di interfaccia (fino ad ora le due cose sono sempre andate di pari passo), chi accede al sito si accorgeva del cambiamento a cose fatte, quasi come una discontinuità di terza specie: una breve interruzione del servizio, che a posteriori sembra non essere mai avvenuta, e che ha permesso ai contenuti pubblicati di continuare a essere visibili e fruibili. Ha aiutato anche il fatto che il cambio sia sempre avvenuto nel corso dell’estate. Questa volta, però, il cambio è stato (e lo è tuttora) più destabilizzante, tanto che mi ritrovo ancora lì, ad arrancare in salita, senza aver fatto il salto, e un po’ timorosa per ciò che mi aspetta dopo la discontinuità. La nuova versione del sito è stata online meno di ventiquattro ore: era troppo piena di problemi tecnici e si è deciso di tornare alla vecchia versione (ma esiste una funzione matematica con una caratteristica simile?). Ora ci stiamo preparando a un passaggio più soft, ancora titubanti dopo il mancato rinnovo.

Mentre nella vita reale i punti di discontinuità o sono imprevedibili o sono preceduti da qualche scossone (che però solo a posteriori puoi leggere come prodromi di una discontinuità), nella matematica è, davvero, tutto più semplice. Penso all’espressione analitica di una funzione, magari una banale funzione algebrica razionale fratta: la guardi e sai già se ci saranno punti di discontinuità. Tutti sono convinti che la matematica sia difficile, ma non è vero: per quanto mi riguarda, la matematica è ordine in mezzo al caos, forse perché il caos lo può descrivere (e, a volte, la descrizione è percepita come una forma di controllo), è regolarità nell’irregolarità e anche nella discontinuità sa offrire delle certezze. Mentre scrivo questa cosa, mi tornano in mente le parole di Christopher Boone, il protagonista di Lo strano caso del cane ucciso a mezzanotte, di Mark Haddon: «Il signor Jeavons disse che mi piaceva la matematica perché mi faceva sentire al sicuro. Disse che mi piaceva perché la matematica serve a risolvere i problemi, poi aggiunse che questi problemi erano difficili e interessanti, ma che alla fine c’era sempre una risposta chiara e diretta per tutto. Ciò che intendeva era che la matematica non è come la vita perché nella vita non esistono risposte chiare e dirette. So che era questo che voleva dire perché è quello che ha detto. Perché il signor Jeavons non capisce i numeri.»

Forse non li ho capiti del tutto nemmeno io…