Visualizza articoli per tag: CdM

Ho pochi ricordi del mio rapporto con la matematica alla scuola primaria, forse perché mi veniva facile e naturale, ma mi è rimasto impresso il disegno alla lavagna di un trapezio e la sua trasformazione in un triangolo equivalente, a spiegare perché per calcolare l’area fosse necessario sommare le basi e moltiplicarle per metà altezza. Forse in quel momento mi sono innamorata della geometria.

I ricordi più vividi sono quelli della scuola media: ricordo quando il professore assegnava delle espressioni da svolgere e le proponeva come sfida alla classe, tanto che in quei momenti, quando capitava che due persone si alzassero nello stesso momento, si assisteva a vere e proprie gare di corsa per raggiungere prima la cattedra. Ricordo, in particolare, che a volte arrivavi alla cattedra, soddisfatto del tuo lavoro e trepidante, ma il professore scuoteva la testa guardando il risultato e allora tornavi al tuo banco per riprovare, intestardendoti alla ricerca della strada corretta.

Del percorso liceale ricordo che l’errore in matematica ha cominciato a presentarsi con una maggiore frequenza, se penso ai problemi di geometria euclidea e analitica o di trigonometria, magari con tanto di discussione e sistemi parametrici al seguito. Capitava di intestardirsi su un problema che non dava il risultato corretto: al mattino, condividevo la mia frustrazione con mia cugina, che era in una classe parallela alla mia, e mi confrontavo con lei, che magari stava litigando con lo stesso problema (avevamo lo stesso insegnante) e ne parlavamo, ripercorrendo insieme le fasi della soluzione, mentre camminavamo verso la scuola. A volte succedeva che trovassimo la soluzione prima di arrivare in aula, e trascrivere i passaggi sul quaderno era solo la conferma di quanto avevamo già capito lungo il cammino. Altre volte, ancora, mi capitava di continuare a pensare al problema durante tutto il pomeriggio, senza riuscire a trovare una soluzione, ma al mattino mi svegliavo con la consapevolezza di conoscere quella soluzione e, prendendo in mano carta e penna, verificavo i passaggi, prima ancora di essere completamente sveglia: è stato in quel momento che ho capito l’importanza del “dormirci su”. Ancora adesso, con maggiore consapevolezza, se ho un problema che non riesco a risolvere (che sia di matematica o di altro) ci penso un attimo prima di addormentarmi, perché la mia testa possa continuare a lavorarci mentre riposo. È la stessa strategia che suggerisco ai miei alunni (per quanto, durante una verifica sia un po’ più difficile riuscire a “dormirci su”…). Mi fa ripensare a Poincaré che, dopo essersi concentrato a lungo e inutilmente su un problema, decise di partire per un gita e, mettendo piede sull’omnibus di Coutances, riuscì a trovare la soluzione (secondo il racconto fatto nel libro Le ostinazioni di un matematico, che racconta l’originale storia di Armand Duplessis, che avrebbe sprecato la propria vita nel tentativo di dimostrare la congettura di Goldbach).

Credo si sia colto il comune denominatore di questi tentativi: la testardaggine… e se penso al percorso universitario, questa mia caratteristica ha avuto un ennesimo banco di prova. Mi sono ritrovata nelle parole di Roberta Fulci che, durante la diretta con Ilaria Fanelli, Una matematica a Radio3 Scienza, ha risposto alla domanda di uno spettatore che chiedeva di essere rassicurato in merito alle sue difficoltà universitarie: Roberta ha raccontato che, avendo scelto matematica dopo il liceo classico, si è trovata ad affrontare grandi difficoltà durante il primo anno di corso ed ha avuto la sensazione di passare “dall’essere brava all’essere un rapa”. Come al solito, Roberta ha espresso il concetto in modo colorito e simpatico, come è tipico suo, e io ho capito perfettamente cosa intendesse, perché l’ho provato sulla mia pelle, anche se avrei dovuto essere più facilitata di lei, visto che alle spalle avevo un liceo scientifico! In realtà, arrivare alla fine del mio percorso universitario, alla tanto desiderata laurea in matematica, ha richiesto un bel po’ di caparbietà, tanto che a chi mi chiedeva che cosa avessi imparato dal mio percorso universitario rispondevo: “Ho imparato ad abbattere i muri a testate”.
Ho concluso il percorso universitario, nonostante… nonostante tutto! Per questo, forse, ho sempre ritenuto la caparbietà una componente fondamentale della buona riuscita in matematica. Addentrandomi sempre più nella storia della matematica, ho scoperto che essa è costruita sulla determinazione, sulla tenacia, sulla caparbietà. Uno dei primi libri che ho letto è L’ultimo Teorema di Fermat di Simon Singh: i tentativi di dimostrare il teorema si dipanano lungo i secoli, dando luogo a una staffetta espressione di un lavoro corale, come se ognuno dei matematici che ha preso parte a questo percorso avesse contribuito alla soluzione del puzzle apportando la propria piccola tessera, fino ad arrivare al risultato finale di Andrew Wiles. Per questo, forse, si parla di comunità matematica, pensando a quelle occasioni in cui i singoli matematici concentrano tutti le proprie forze per raggiungere un obiettivo comune, attraverso un lavoro continuo.

La mia convinzione che determinazione e caparbietà possano essere un’arma vincente anche a scuola mi ha portato a proporre, all’inizio di ogni percorso scolastico, una citazione di John Wooden, uno dei più grandi allenatori nella storia del basket delle università americane:

«Quando si migliora un po’ ogni giorno, alla fine si raggiungono grandi risultati. Quando si aumenta l’allenamento giorno dopo giorno, si ottiene un netto miglioramento della forma fisica. Non sarà domani, né dopodomani, ma poi i progressi saranno notevoli. È inutile puntare a grandi risultati in tempi brevi, conviene invece cercare di migliorare un po’, un giorno dopo l’altro. È l’unico modo per ottenere risultati duraturi.»

Gigliola Staffilani, prima donna italiana full professor al MIT, alla domanda rivoltale da Roberto Natalini in un’intervista del 2018 «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?» ha dato una bella risposta: «Credo che l’intuizione arrivi quando ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte.» Secondo la leggenda, pare che al re Tolomeo, che chiedeva un metodo rapido per studiare la geometria, Euclide abbia risposto che non esistono “vie regie”, ovvero percorsi privilegiati: in altre parole, ci sono stati matematici grandissimi nella storia, ma questo non significa che per loro le cose siano state più facili, perché avevano talento. Il duro lavoro resta una componente fondamentale per la buona riuscita in matematica!

Nei giorni scorsi, durante una lezione nella mia terza liceo scientifico, mentre le idee continuavano ad accumularsi intorno al tema della caparbietà, ho chiesto ai miei alunni quale potesse essere la caratteristica che una persona deve possedere per garantirsi un successo in matematica. Sono rimasta molto colpita dalle loro risposte: innanzi tutto perché molti di loro, invece di indicarmi una caratteristica, hanno risposto fornendo una strategia, che passava attraverso il ragionamento, la comprensione o la spesa di un po’ di tempo per creare collegamenti mentali, ma qualcuno ha risposto: «bisogna sapere le regole per poterle applicare meccanicamente» e, davanti alle mie proteste, si è difeso parlando di una strategia personale. Mi ha colpito, inoltre, che qualcuno ritenga importante il calcolo o “farsi piacere la matematica”, perché se è vero che, per certi aspetti, l’apprendimento è reso più facile dalla passione, non è certo possibile imporsi a comando di amare una disciplina. Dopo aver indicato la necessità di fare molti esercizi, qualcuno ha parlato di perseveranza e costanza, della capacità di non abbattersi per un risultato negativo, di forza di volontà e determinazione… e poi c’è il mio foglietto con scritto: caparbietà.

Ho voluto approfittare di queste risposte per riflettere con loro, a partire dalla storia di Sophie Germain (è mia intenzione partecipare a #peopleformath2024 lanciato dal canale IlariaF Math…). La sua vicenda biografica ha tutte le caratteristiche di un romanzo, con l’assunzione dell’identità di Antoine Le Blanc, per poter interloquire con i matematici più importanti dell’epoca come Lagrange e Gauss, e per approfondire la sua vita ho fatto riferimento al libro di Cecilia rossi Sophie Germain. Libertà, uguaglianza e matematica.

Al momento di costruire una bibliografia, mi sono imbattuta anche in Nothing stopped Sophie, di Cheryl Bardoe, con le illustrazioni di Barbara McClintock: si tratta di un libro per bambini, disponibile solo nella versione inglese, nel quale troviamo, ripetuto più volte, “Nothing stopped Sophie”, perché effettivamente niente riuscì a fermarla! Nel momento in cui i suoi genitori hanno cercato di ostacolarla nella sua passione per la matematica, lei ha trovato il modo di andare avanti, ad esempio.

Le donne che hanno scritto di lei considerano la caparbietà uno dei suoi lati più positivi, ma non è così se la sua vicenda viene interpretata da uomini: nel libro Il genio delle donne, Piergiorgio Odifreddi ha dedicato alla Germain il capitolo La prima vera matematica, ma non le risparmia il suo sarcasmo, visto che la definisce una giovane dal «carattere difficile e [dai] modi arroganti». Parlando poi del suo scontro con l’astronomo Joseph de Lalande, che l’aveva omaggiata del suo “Astronomia per le dame”, una delle pubblicazioni dell’epoca che trattava le donne con condiscendenza e proponendo una divulgazione in versione semplificata, dice che lei «disdegnava i testi divulgativi, e rivolse presto la sua attenzione alle difficili Disquisizioni aritmetiche», come se in realtà Sophie Germain peccasse di presunzione e non fosse realmente in grado di comprendere un testo del genere. Come insegnante ho imparato a considerare la presunzione e l’arroganza una necessità, per i giovani: senza presunzione, non potrebbero mettere in dubbio i tanti “ipse dixit” con i quali si trovano a confrontarsi quotidianamente, e senza un po’ di arroganza non avrebbero il coraggio di competere con gli adulti. Franco Pastrone, del Dipartimento di matematica dell’Università di Torino, nel suo intervento per l’Associazione Subalpina Mathesis, che è diventato l’introduzione nel libro di Maria Rosa Menzio Il Signor Le Blanc, ha un giudizio a tratti tranchant: riferendosi all’infanzia, parla di episodi «forse un po’ forzati al fine di esaltare la determinazione della ragazza», che descrive come una persona timida in pubblico, anche se, quando si trattava di ottenere dei risultati scientifici «la sua timidezza scompariva, anzi riusciva a mostrare una cocciuta aggressività».
Mi è parso quasi di cogliere che questa caparbietà, così positiva quando esercitata dagli uomini, diventasse un aspetto quasi negativo se declinato al femminile. Eppure, quando parliamo di Andrew Wiles, la sua determinazione viene celebrata, e la sua capacità di isolarsi dal resto del mondo per lavorare in autonomia alla dimostrazione non viene presa per presunzione, semmai gli viene riconosciuto il coraggio di aver rischiato tanto. Andrew Wiles ha avuto il coraggio di affrontare una sfida che aveva attraversato i secoli e, quando viene individuato un errore nella sua dimostrazione, prova a correggersi, impegnando altro tempo.

Non parla di presunzione, Gauss che, una volta conosciuta l’identità di Sophie Germain, le scrive:

«Il fascino di questa scienza sublime si rivela in tutta la sua bellezza solo a chi ha il coraggio di esplorarla. Una donna, a causa del suo sesso e dei nostri pregiudizi, incontra molti più ostacoli di un uomo nel familiarizzarsi con problemi complessi. Tuttavia, quando supera queste barriere e penetra nelle profondità più recondite, rivela di possedere il coraggio più nobile, un talento straordinario e un genio superiore.»

Per concludere, non può mancare un riferimento all’ultimo premio Abel, Michel Talagrand, che dichiara che «il segreto del successo in matematica è di lavorare ogni giorno fino a essere esausti ma non di più». Ne parlano, con dovizia di particolari, Beatrice Mautino ed Emanuele Menietti nel podcast del Post Ci vuole una scienza: Talagrand parla delle proprie difficoltà in matematica, legate a un “cervello lento” e a una “memoria terribile”, eppure dichiara di aver usato questo metodo proprio per superare le sue difficoltà. E direi che, visti i successi, non ci resta che fidarci!

Ricordo ora che anche Maryam Mirzakhani si è sempre definita una matematica lenta, ma è riuscita, nella sua breve vita, a raggiungere risultati eccezionali. Alex Eskin, dell’Università di Chicago, con il quale ha collaborato a lungo, racconta, nel film Secrets of the Surface, l’esperienza di lavoro con Maryam, paragonando il loro percorso a una camminata in montagna. Si trattava, come spesso succede, di una montagna inesplorata, e, a un certo punto, i due matematici hanno avuto l’impressione di poter raggiungere agevolmente la cima, quando un burrone ha sbarrato loro la strada. Con un sorriso dolce-amaro, Eskin racconta lo scoraggiamento che hanno provato, dato che quel burrone è costato loro due anni di duro lavoro e fatica. In tutto questo, Maryam si è mostrata positiva, anche se per un anno mezzo non ci fu nessun tipo di progresso. Per affrontare una fatica del genere e uscirne vittoriosi, è necessario avere una grande stabilità mentale e fiducia in sé stessi.

Aggiungendo queste caratteristiche alla caparbietà, credo proprio che il successo sia assicurato!

Si può dire che p sia il protagonista del programma di seconda liceo scientifico: nella prima parte dell’anno scolastico, ci si immerge nell’insieme dei numeri reali e gli irrazionali sono posti al centro della scena. Come dimenticare l’irrazionale per eccellenza?

Nell’immagine è riportata una rappresentazione visiva di alcune cifre decimali di p, 180 per la precisione, che è facile ricostruire assegnando al colore la cifra corrispondente. L’immagine è stata realizzata per uno dei cartelloni esposti durante la seconda partecipazione al Festival di BergamoScienza dell’istituto dove insegno, che ha avuto come protagonista il cerchio.

La classe seconda è il momento in cui si alza il livello di difficoltà: dopo aver risolto equazioni, disequazioni e sistemi lineari, si affrontano, con gli irrazionali nella cassetta degli attrezzi, i problemi di secondo grado ed ecco che in geometria fa la sua comparsa la circonferenza, definita come il luogo geometrico dei punti del piano equidistanti da un punto fisso, il centro.

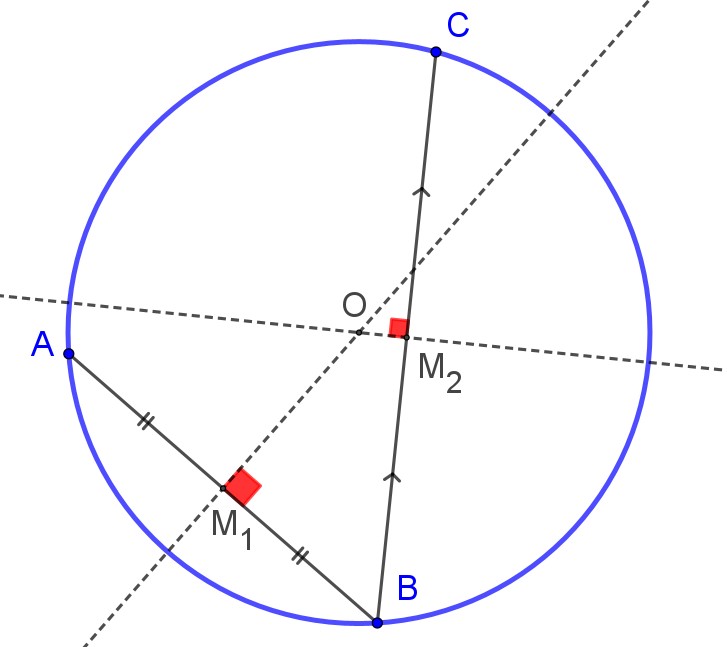
Uno dei primi teoremi che si incontrano riguarda la circonferenza passante per tre punti non allineati, e la dimostrazione permette, in realtà, di fare una semplice costruzione con Geogebra, evitando di usare lo strumento “Circonferenza – tre punti”. Il teorema fa intravedere i teoremi sulle corde, che presto permetteranno di vederne la lunghezza in relazione alla loro distanza dal centro, e di realizzare che davvero l’asse di una corda passa per il centro.

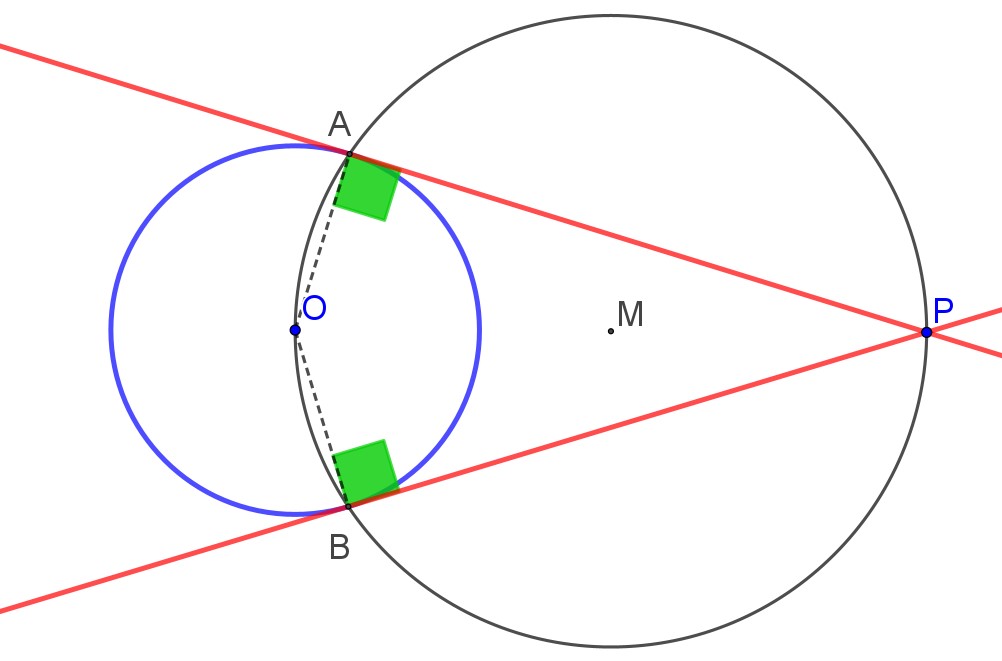
Il passo successivo è quello di considerare le circonferenze in relazione alle rette e, in particolare, in relazione alle tangenti. Così, può capitare di dover imparare a costruire le rette tangenti a una circonferenza tracciate da un punto esterno, basandosi sul fato che una retta tangente a una circonferenza è perpendicolare al raggio passante per il punto di tangenza. Questo risultato ci regala un anticipo sui triangoli rettangoli inscritti in una semicirconferenza.

Il percorso in matematica assomiglia a una danza, con un passo avanti e uno indietro, a creare una coreografia, ritornando su cose già viste, ma affrontandole in maniera diversa, e così nel capitolo successivo le circonferenze incontrano i triangoli, sempre inscrivibili in e circoscrivibili a una circonferenza, ma non solo:

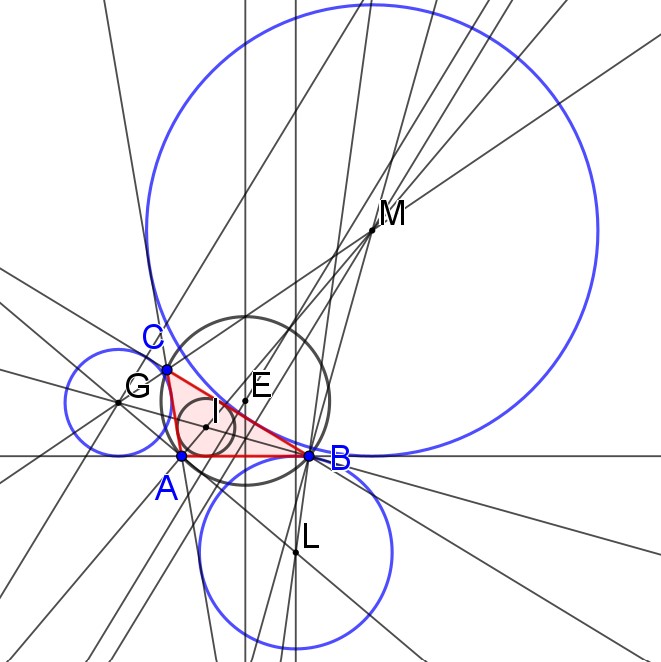
Tra il circocentro (E) come punto di incontro degli assi e centro della circonferenza circoscritta, l’incentro (I) punto di incontro delle bisettrici e centro della circonferenza inscritta, il triangolo ABC incontra anche altre tre circonferenze, di centri rispettivamente M, L e G, detti excentri, punti di incontro della bisettrice dell’angolo interno non adiacente con le bisettrici degli altri due angoli esterni e quelle blu sono le circonferenze exinscritte, tangenti a un lato e al prolungamento degli altri due. È stato vedendo un’opera di Lanfranco Bombelli (1921/2008), pittore, incisore e architetto, che ho pensato a questa rappresentazione e…

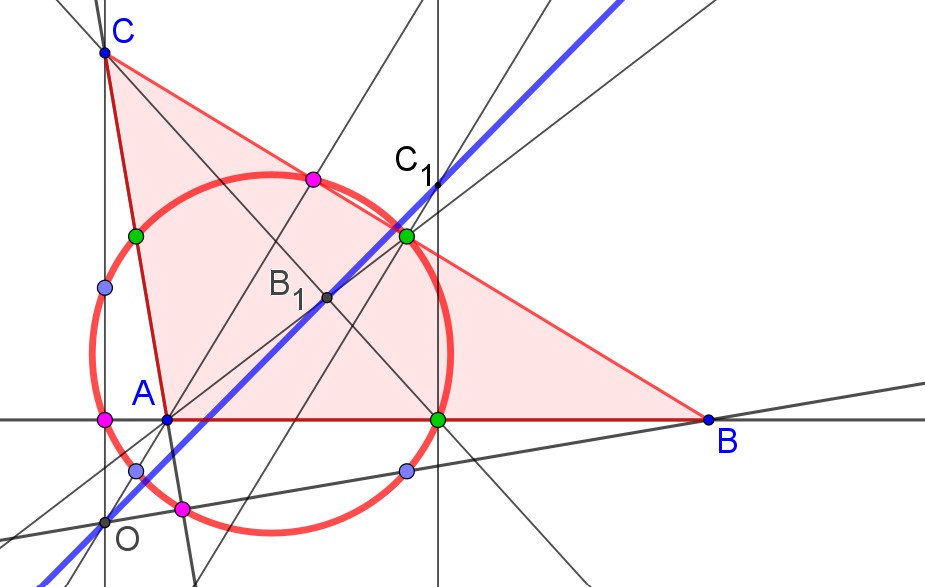
Ripensare al Cerchio per nove punti è stato un attimo: eccola in tutta la sua bellezza! Indicata in rosso passa per tre terne di punti: quelli rappresentati in verde sono i punti medi dei lati del triangolo; quelli in fuxia sono i piedi delle altezze relative ai lati e poi ci sono gli ultimi, più difficili da definire, perché, individuato con O l’ortocentro (il punto di incontro delle altezze di un triangolo), essi sono i punti medi del segmento che ha per estremi O e un vertice del triangolo. Ho scoperto, giusto oggi, che questa circonferenza è nominata come Cerchio di Feuerbach (almeno, stando a quanto dichiarato su Wikipedia), matematico tedesco, fratello del più famoso filosofo. Qualcuno, invece, la nomina come cerchio di Eulero, ma credo che, in questo caso, il celebre matematico potrebbe accontentarsi della paternità della retta, che passa per tre punti notevoli: ortocentro, baricentro, circocentro.

Mentre scorro le pagine del libretto di Bruno Munari intitolato Il cerchio (e scopro ora che ci sono anche Il quadrato e Il triangolo…) dove ho trovato il riferimento a Lanfranco Bombelli, mi imbatto nelle voci “Raggio decrescente” e “Raggio crescente”:

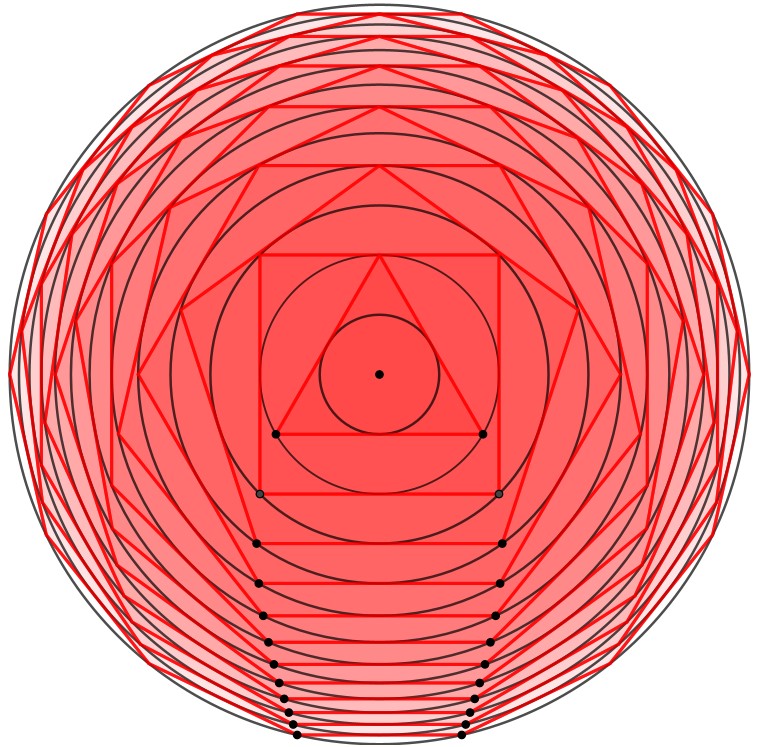
Mi è parso così interessante, che non ho resistito alla tentazione di realizzare quello crescente con Geogebra, arrivando fino al poligono di 14 lati (inventandomi metodi ingegnosi per rappresentare quelli da 7, 9, 11 e 13 lati). Mi piace citare, in particolare, ciò che scrive Munari, oltre alle indicazioni per la costruzione: «Può sembrare che il raggio, aumentando oltre ogni limite, diventi infinito; invece si avvicina a un limite che è circa dodici volte quello del raggio del cerchio primitivo», esattamente come quello decrescente «si avvicina a un limite che è circa un dodicesimo di quello del raggio del cerchio primitivo».

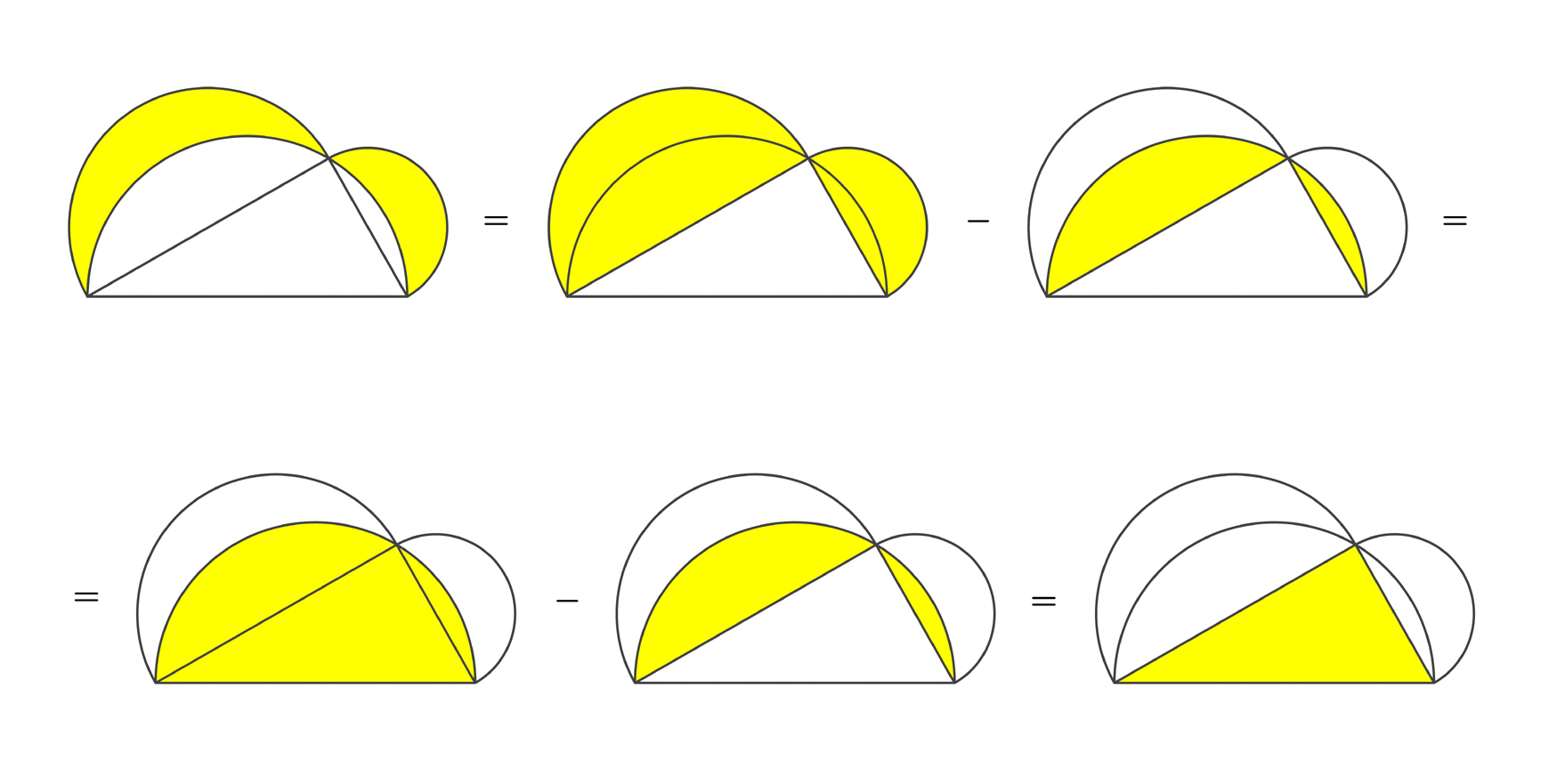
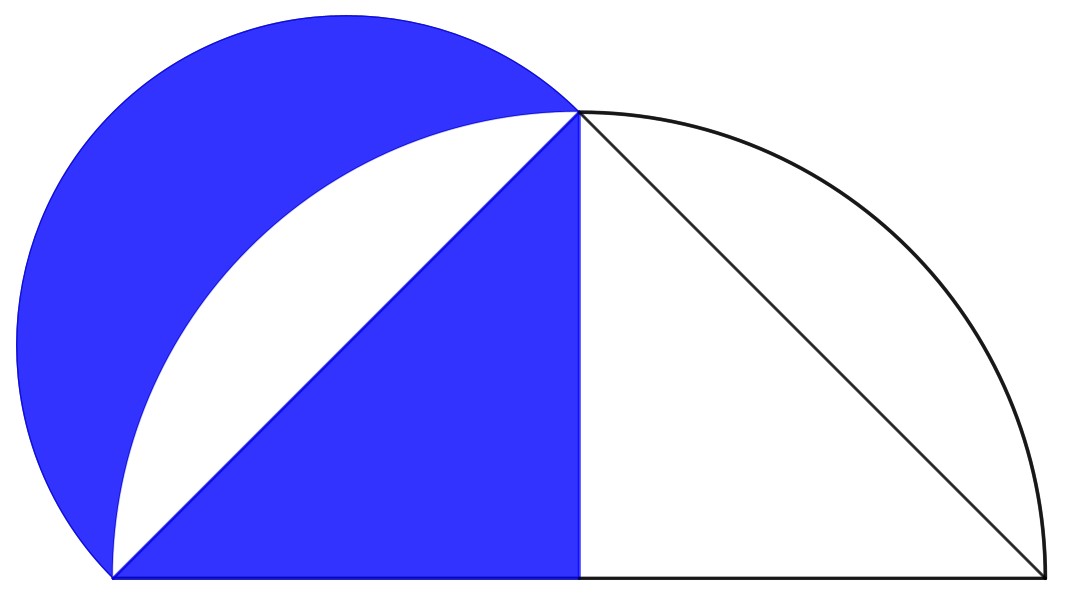
Non ho resistito alla tentazione di riprendere in mano anche questa simpatica dimostrazione senza parole, che utilizza le lunule e il triangolo di Pitagora. Il triangolo rappresentato è rettangolo e ha come lato di appoggio l’ipotenusa. Sui due cateti vengono costruite (e colorate) le lunule, la «parte di piano compresa fra due archi circolari di raggio diverso aventi in comune gli estremi e giacenti dalla stessa parte rispetto alla corda comune». In questo caso, il raggio delle semicirconferenze esterne è pari a metà del cateto e il centro è il punto medio del cateto, mentre l’arco più interno è la semicirconferenza con raggio pari a metà dell’ipotenusa e centro nel punto medio della stessa. La prima differenza è facile, la seconda, invece, ha a che fare con il teorema di Pitagora: come riportato sul sito del Giardino di Archimede, il museo della matematica: «Nell’enunciato del teorema di Pitagora, i quadrati possono essere sostituiti da altre figure, come ad esempio triangoli, esagoni, o anche figure irregolari, purché simili tra loro». Chi ha avuto modo di visitare il museo, avrà provato a mettersi alla prova con i diversi puzzle realizzati proprio con questo teorema di Pitagora generalizzato.

Sul sito, troviamo poi il caso particolare delle lunule di Ippocrate:

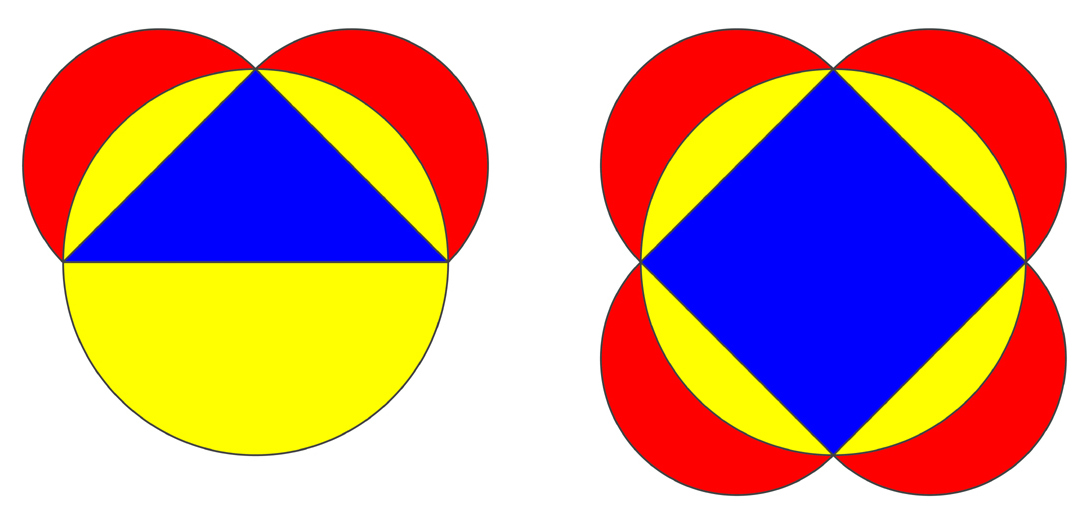
In questo caso, l’area indicata in rosso ha la stessa estensione di quella indicata in blu.

«Se poi il triangolo è isoscele, una lunula è uguale a mezzo triangolo. Questo è il primo caso storicamente accertato (la dimostrazione è attribuita a Ippocrate di Chio) in cui si è dimostrato che una figura rettilinea (il triangolo) è uguale a una curvilinea (la lunula).» Questo ci porta al logo della Mathesis:

Una scelta non casuale, visto che la Mathesis è la «Società italiana di scienze matematiche e fisiche fondata nel 1895».

Il 14 marzo è, dal 2020, la Giornata internazionale della matematica e quest’anno il tema dei festeggiamenti è: Giocare con la matematica. Non potevano mancare un paio di giochi, in chiusura, presi dalle ultime due edizioni di Matematica senza Frontiere:

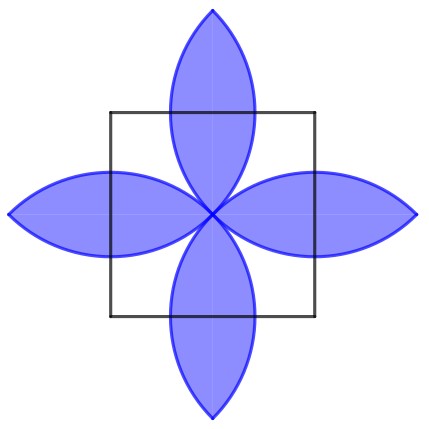
L’immagine a sinistra è stata proposta quest’anno: dopo averne indicato la costruzione, si chiedeva di determinare l’area della parte colorata, in funzione del lato del quadrato (indicato con a). continuando la tassellazione con altre circonferenze, è stato abbastanza semplice sottrarre, dall’area della circonferenza con raggio pari a metà diagonale del quadrato, un quadrato di lato a e moltiplicare il risultato per 2, ottenendo . Il disegno più colorato, invece, è stato proposto nella competizione dell’anno scorso e dovrebbe rappresentare la finestra con il vetro temperato di una chiesa. Sapendo che per il verde sono stati usati 400 cm² di vetro, che superficie è necessaria per ricoprire il blu? (E scopriamo che si tratta ancora di 400 cm²).

Il cerchio è davvero una figura eccezionale e Munari dichiara nell’introduzione del suo libretto: «Il cerchio è una figura essenzialmente instabile, dinamica: dal cerchio nascono tutti i ruotismi, tutte le inutili ricerche del moto perpetuo». E dal cerchio è giunto a noi p, come dimenticarlo?

Buon pi-day a tutti!

PS: In allegato i file Geogebra per realizzare le immagini