Nonostante abbia pensato spesso agli origami come ad un’attività che poteva avere qualche risvolto significativo, dal punto di vista matematico, solo alla scuola primaria o, al massimo, per la scuola secondaria di primo grado, mi è capitato di cercare dei libri che proponessero attività laboratoriali, magari da usare durante un’edizione di BergamoScienza. Poi ho conosciuto Sonia Spreafico autrice, insieme a Emma Frigerio, di Ed ora, origami e ho trovato, su suggerimento proprio di Sonia, un’attività da proporre alla mia quarta liceo scientifico, che sta muovendo i primi passi nel mondo della goniometria. Già dopo la prima attività, ho capito che le potenzialità sono davvero grandissime!

Ho cominciato con l’attività della costruzione di un goniometro (presentata a pagina 100 del suddetto libro) e i ragazzi si sono lasciati coinvolgere abbastanza facilmente, forse incuriositi dai foglietti colorati, e, nonostante fosse l’ultima ora di lezione, hanno partecipato con entusiasmo, rispondendo a tutte le mie domande e individuando gli angoli noti. Da lì in poi, è stato facile far loro ricavare seno, coseno e tangente degli angoli di 30°, 60° e 45°, ponendo uguale a 1 il lato del foglietto.

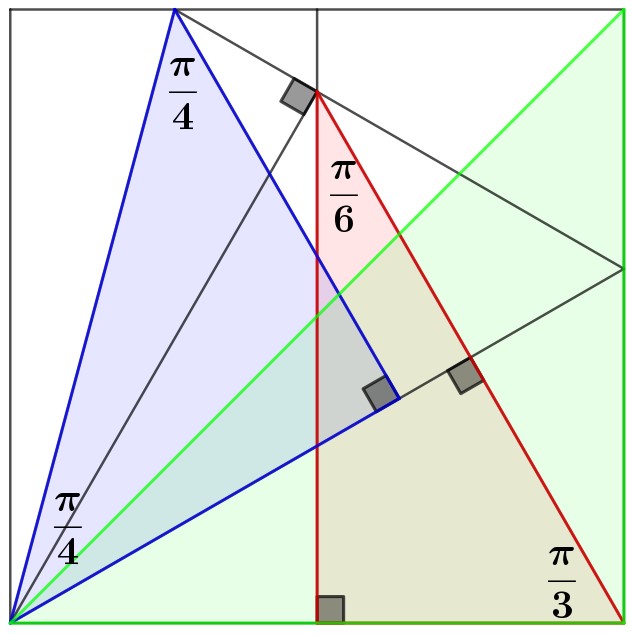
Con le funzioni dell’angolo di 45° abbiamo giocato un po’, perché partire dal triangolo indicato in blu nel disegno precedente implica confrontarsi con i (tragici) radicali doppi e ragionare bene con la geometria euclidea; perciò, qualcuno ha pensato bene di scegliersi il triangolo verde e risolvere il problema… alla radice!

Mentre i ragazzi piegavano e calcolavano, ho pensato a un modo per proporre gli archi associati che potesse sfruttare ancora gli origami, considerando anche la disponibilità delle due ore di lezione consecutive. La mattina dopo, quindi, mi sono presentata in aula con un bel po’ di foglietti colorati e, come prima cosa, i ragazzi si sono divertiti a scegliere il colore preferito.

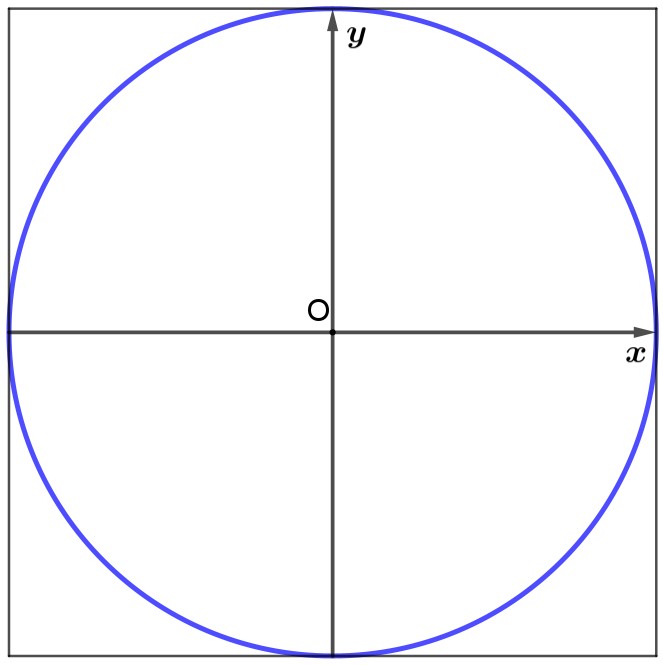
Tutto è cominciato con due pieghe centrali, per ottenere gli assi cartesiani e poter rappresentare la circonferenza goniometrica: oggi il lato del quadrato ha misura 2, a differenza di ieri.

Il secondo passo è stato quello di individuare un angolo a, con l’unico vincolo di essere nel primo quadrante: si è trattato di realizzare una piega che passasse per il centro della circonferenza.

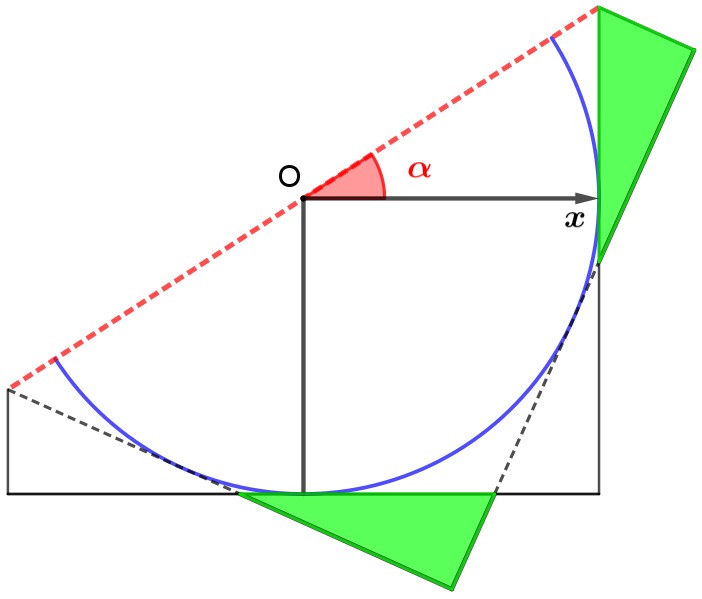
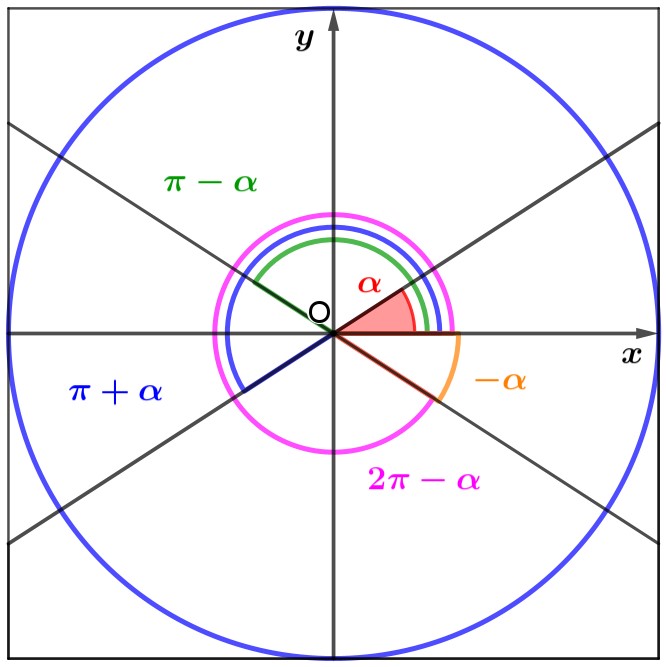
La sfida era quella di rappresentare gli angoli supplementare ed esplementare dell’angolo dato, e l’angolo che differisse da questo di un angolo piatto, con il limite di non poter usare righelli e matite, ma di doversi limitare alle pieghe. Non è stato difficile capire di dover usare l’asse x come asse di simmetria per poter individuare l’angolo esplementare:

I quattro archi associati ad a sono stati così individuati senza grossi problemi.

L’ultimo passo è stato quello di effettuare delle pieghe, parallele ai lati del quadrato, che passassero per le intersezioni delle pieghe precedenti con la circonferenza,

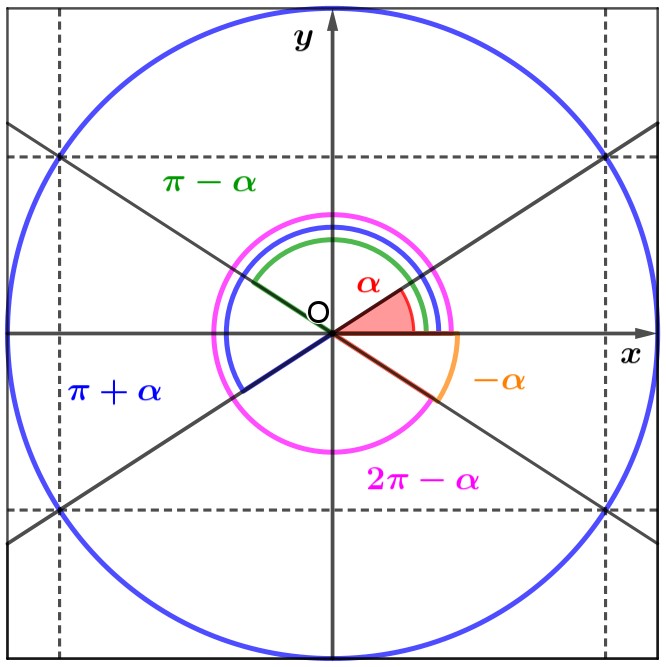
per poter riconoscere le funzioni goniometriche degli archi associati in funzione di quello di partenza.

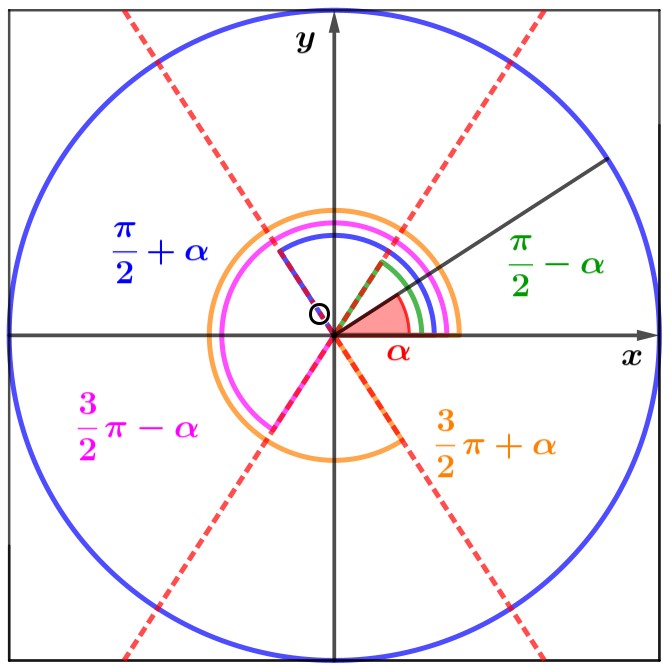
Acquisita un po’ di confidenza con lo strumento ed avendone colta la potenzialità, la classe ha risposto con rinnovato entusiasmo alla seconda sfida: individuare gli archi collegati ad a da somme e sottrazioni di angoli retti e loro multipli dispari. Siamo partiti con il vincolo, per a, di essere minore di un angolo di 45°, ma non era realmente necessario. Qualcuno, non avendo colto questa richiesta, si è ritrovato poi con un rettangolo “sdraiato” invece che “in piedi”, ma è stato rassicurato da chi, in precedenza, aveva ottenuto un rettangolo “in piedi” laddove tutti avevano trovato quello “sdraiato” (traduzione matematica: rettangolo “sdraiato”, ovvero rettangolo con la base maggiore dell’altezza; rettangolo “in piedi”, ovvero con la base minore dell’altezza).

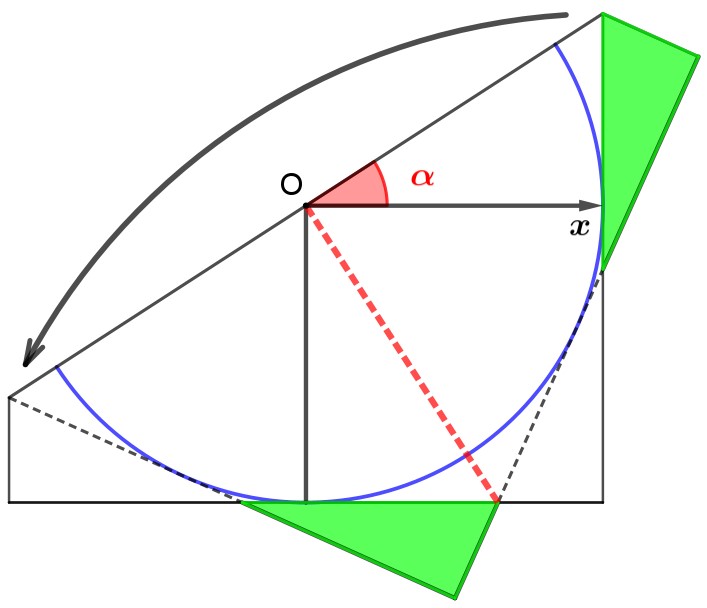
Il primo obiettivo è stato quello di individuare l’arco che differisce di un angolo retto dall’angolo dato, e, avendo finalmente capito come effettuare la piegatura per ottenere l’asse di un segmento, è stato sufficiente piegare a metà la figura ottenuta dalla piega di a per ottenere l’angolo richiesto.

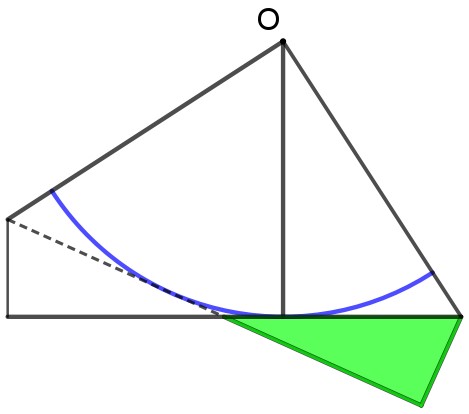
Dopo aver individuato l’angolo richiesto, non ci è voluto molto per individuare la somiglianza con quanto fatto prima e trovare così gli altri tre angoli associati.

Anche dimostrare la congruenza dei triangoli rettangoli presenti nella figura, per poter individuare le funzioni goniometriche dei nuovi angoli, è stata una richiesta nata proprio dagli studenti, che hanno “sopportato” meglio il linguaggio della geometria euclidea, vissuta in questo caso come un aiuto, più che come un’incombenza necessaria.

L’ultimo passo, questa volta assegnato da svolgere in autonomia a casa con un foglietto origami in omaggio, è stata la riduzione al primo quadrante di angoli noti.

In questo percorso, la fantasia ha agevolato la memoria e favorito la comprensione, ma per concludere degnamente l’attività, abbiamo chiuso le due ore con quattro manches a Seni in fila, uno dei giochi proposti proprio da Sonia Spreafico e Paola Morando (presenti su Instagram con il profilo Giochi e pieghe). Per una volta, le due ore di matematica sono state vissute in leggerezza!

Un capomastro lavorava da molti anni alle dipendenze di una grossa società edile. Un giorno ricevette l’ordine di costruire una villa esemplare secondo un progetto a suo piacere. Poteva costruirla nel posto che più gradiva e non badare alle spese.
I lavori cominciarono ben presto. Ma, approfittando di questa cieca fiducia, il capomastro pensò di usare materiali scadenti, di assumere operai poco competenti a stipendio più basso, e di intascare così la somma risparmiata.
Quando la villa fu terminata, durante una festicciola, il capomastro consegnò al Presidente della società la chiave d’entrata.
Il Presidente gliela restituì sorridendo e disse, stringendogli la mano: «Questa villa è il nostro regalo per lei in segno di stima e di riconoscenza».

Bruno Ferrero, «C’è qualcuno lassù?», Editrice Elle Di Ci

Quando Marco Menale ha lanciato il tema di questo Carnevale della Matematica, «Matematica e Futuro», ha detto di declinarlo come si preferiva: «tempo verbale, congetture da risolvere, nuove teorie, IA, vita su Marte ecc ecc». Dopo qualche giorno di riflessione, ho realizzato che, in quanto insegnante, il futuro lo tocco con mano ogni giorno, contribuendo a plasmarlo, ma cosa può avere a che fare questo con la matematica?

Nel momento in cui ho scelto il mio di futuro, non ho scelto solo di studiare matematica e non ho scelto di fare l’insegnante, ho scelto di fare l’insegnante di matematica: le due cose sono state, per me, inscindibili da subito. Quando ho fatto questa scelta, frequentavo le scuole medie e avevo un’idea molto limitata della matematica: fondamentalmente, mi piaceva svolgere espressioni e piccoli problemi, e ho mantenuto la passione anche al liceo, nonostante abbia riflettuto ultimamente su quanto sia più facile far amare la fisica, rispetto alla matematica. La fisica si presenta, almeno all’inizio, con una veste abbastanza semplice, richiedendo poco più dell’algebra per la soluzione di problemi che descrivono una realtà ovattata. Eppure, anche se limitata da piani senza attrito e moti perfettamente uniformi, la fisica conquista e affascina, perché tenta una descrizione della realtà. Ben diverso è il percorso della matematica, che mostra fin da subito il suo lato spinoso. Chi si diverte con il calcolo, spesso prosegue alle superiori con l’algebra senza troppi intoppi, ma chi rifugge il rigore, rischia di restare incastrato nei meccanismi del calcolo letterale. Poi ci si scontra con la geometria analitica e con i problemi: da studenti che subiscono passivamente equazioni e disequazioni, gli alunni sperimentano quanto diceva Maryam Mirzakhani, «Fare matematica per me è come una lunga escursione senza un sentiero tracciato né un traguardo visibile». All’ultimo anno poi, lo studio di funzione costituisce l’apice del percorso e dell’astrazione, ed offre l’opportunità di effettuare quegli approfondimenti che non hanno trovato spazio in precedenza. Ma l’esame di stato è alle porte e, che si sia studenti in un liceo scientifico oppure no, tutto viene assorbito da quello e non resta spazio per far amare questa splendida disciplina. E così, anche noi insegnanti in qualche modo diventiamo oggetto di questo odio, che non si capisce più se nasca contro la matematica e poi si estenda anche a noi, o se siamo noi insegnanti che non siamo capaci di generare simpatia, né per noi né per la nostra disciplina.

Temo che questo “odio” abbia a che fare con la richiesta di semplificazione che arriva da più parti, una sorta di ricerca di riassunti, schemi, che possano aiutare a capire, ma, al tempo stesso, rendere più veloce il tempo di apprendimento. Credo che la chiave del problema sia proprio in questa “fretta”: il processo di apprendimento in generale, non solo quello della matematica, richiede tempo e pazienza e, a volte, costa fatica, e cercare di spianare la strada ai nostri alunni non li aiuta a imparare. Qualcuno più famoso di me, e molto prima di me, l’ha detto meglio: «Non esistono vie regie»!

Sono consapevole di non essere la sola a vivere questa fatica, come ha ben dimostrato su Facebook un post del 15 ottobre scorso di Giuseppe Mingione, docente di Analisi all’Università di Parma: dopo aver richiesto la soluzione di un semplice esercizio ai suoi studenti e non averne ottenuto alcuna risposta, l’ha somministrato a ChatGPT, ottenendone una soluzione perfetta. Ha quindi chiesto ai suoi studenti che compito si assumerebbero e quale affiderebbero a ChatGPT, tra risolvere esercizi e raccogliere pomodori: «i ragazzi hanno stavolta correttamente risposto, e, preoccupati, hanno capito cosa sta succedendo».

Non ho potuto non parlare in classe di questo post, invitando i miei studenti a riflettere sul fatto che la scelta di studiare determinati argomenti ci permette di ampliare il ventaglio di possibilità che il futuro ci offre. Resto sempre un po’ perplessa quando, arrivati all’ultimo anno di liceo, alcuni miei alunni, posti di fronte alla scelta del percorso da seguire all’università, vanno alla ricerca del corso di laurea che non prevede un esame di matematica. Ho ritrovato questo mio malessere ben argomentato, proprio ieri, da Federico Benuzzi, che ha raccolto, al termine di un suo spettacolo, la frase, pronunciata da un alunno di una terza media: «Andrò al linguistico perché c’è poca matematica». Benuzzi dà voce a questa frustrazione scrivendo: «il percorso di studi si sceglie “per”, non “contro”».

Quando dico che, come insegnante, plasmo il futuro, non mi riferisco, però, solo al futuro dei miei studenti: a loro tento di dare quegli strumenti che, credo, saranno fondamentali non solo per la loro professione, ma per la loro vita, e nel costruire qualcosa per loro costruisco anche qualcosa per me, come il capomastro del racconto iniziale. Il mio pensiero torna a quel giorno in cui, in pronto soccorso, sono stata accolta da un ex alunno che lì lavorava come infermiere: quando guardo i miei alunni, nell’età più ingrata della loro vita, cerco di non dimenticare che un domani saranno adulti, e potrebbero essere direttori/direttrici della casa di riposo in cui passerò gli ultimi anni della mia vita.

Facendo l’insegnante di matematica, sento di contribuire a costruire la vita dei ragazzi attraverso la matematica, anzi sono consapevole che sarà proprio la matematica ad offrire loro una vita diversa. Sempre citando Giuseppe Mingione: «una maggiore alfabetizzazione matematica serve anche a difendersi da certe frottole ben raccontate».

Abraham Lincoln, politico e avvocato statunitense nonché sedicesimo presidente degli USA, scrisse una celebre lettera all’insegnante di suo figlio il primo giorno di scuola. Alla ricerca di idee per questo articolo, non potevo non restare colpita da questa edizione per bambini della Einaudi, suggerita sul suo profilo Instagram da Alessandro Barbaglia, autore de L’invenzione di Eva, romanzo e biografia di Hedy Lamarr: «Gli insegni, se può, che 10 centesimi guadagnati valgono molto di più di un dollaro trovato; a scuola, o maestro, è di gran lunga più onorevole essere bocciato che barare.» La scuola è un ambiente protetto, nel quale è importante che vengano proposte sfide, anche al di sopra delle proprie capacità: è come una palestra nella quale ci si allena a vincere le gare della vita, costruendo strumenti importanti per il futuro.

Rileggendo ciò che ho scritto fino ad ora, mi rendo conto che nella mia vita la matematica, forgiando il mio passato, mi ha permesso di costruire un presente nel quale ho il potere di plasmare il futuro. In altre parole, posso declinare la matematica al passato, al presente, al futuro, ma credo che, consapevoli o meno, sia una cosa che ognuno di noi può fare. Mentre ascoltavo la TED-talk di Alberto Saracco, docente di geometria all’Università di Parma, intitolata Matematica per il futuro, riflettevo non solo sull’impossibilità di studiare solo ciò che può essere utile un domani (come si fa a sapere cosa ci sarà non solo utile, ma necessario?), ma mi ponevo anche un’altra domanda: dove si deve fermare lo sguardo? Quando insegno, il mio sguardo non si ferma all’orizzonte dell’esame di stato, ma va oltre, e credo che lo sguardo di un matematico sia simile: i matematici hanno trovato il modo di toccare l’infinito (basti pensare al piano proiettivo), e allo stesso modo possono toccare il futuro, come dimostrato dalla trasformata di Radon-Nikodym del 1917, che è diventata la chiave per uno degli esami diagnostici più importanti, la TAC. Chi avrebbe potuto vedere un futuro così brillante in una matematica così complessa e, per i più, oscura? È sempre Alberto Saracco, nel parlare della ragionevole efficacia della matematica, che dice: «La matematica è potente nel descrivere il mondo e chi sa utilizzarla per il proprio tornaconto ha a disposizione un vantaggio enorme».

Insegno matematica e plasmo futuro ogni volta che propongo sfide, ogni volta che chiedo ai miei studenti di ragionare, ogni volta che stimolo uno sguardo critico sulla realtà, ogni volta che chiedo un piccolo impegno continuo, perché il futuro non si improvvisa, esattamente come una verifica di matematica. Non mi faccio illusioni, però: non ho idea di quanto loro ricordino di ciò che cerco di trasmettere, ma ho imparato che, se dico qualcosa di errato durante una spiegazione (e lo faccio più frequentemente di quanto vorrei), loro lo ricorderanno sicuramente. Purtroppo, questi errori hanno una vita lunga, come dimostrato dal video realizzato pochi giorni fa dal canale Kurzgesagt – In a Nutshell. Il titolo del video rimanda alla «più vecchia bugia di Internet» e racconta della ricerca delle fonti per la frase: «I tuoi vasi sanguigni si estendono per l’incredibile lunghezza di 100.000 chilometri, abbastanza da avvolgere la Terra due volte!» Ci è voluto un anno per trovare l’origine di questa affermazione e non voglio rovinare la sorpresa, ma basti sapere che l’affermazione è nata, innanzi tutto, da una serie di approssimazioni, e si trattava di una cosa di poca importanza inserita in un libro che aveva ben altri meriti. Eppure, ciò che ha trovato la strada per Internet, da un libro di oltre un secolo fa, è stata un'affermazione sbagliata.

Pc collegato al proiettore, sullo schermo è aperto MINECRAFT, davanti al pc Alunno 01, con le cuffie sulle orecchie, concentrata a lavorare alle illusioni prospettiche realizzate.

Prof.1: (voce dal corridoio) Alunno 01! Alunno 01! (Alunno 01 non risponde. La Prof.1 arriva davanti al pc di Alunno 01) Impossibile farsi rispondere da te, vero? (Alunno 01 si toglie le cuffie). Cosa stai facendo? Ancora a pc? (Arrabbiata) Basta con questo computer! È estate! Se non ti decidi a fare altro, te lo brucio!
Alunno 01: Ma mamma, sto lavorando per BergamoScienza!
Prof.1: (di colpo interessata!) Davvero? E cosa stai facendo di bello?
Alunno 01: (mostra alcune delle illusioni realizzate con Minecraft) In questo caso sembra che ci sia un muro. Vedi? Avvicinandomi sembra che il muro diventi sempre più grande.
Prof.1: Vedo! E invece?
Alunno 01: E invece non c’è nessun muro!
Prof.1: Bello! Davvero interessante! (passando ad una nuova slide) Ma questa è la scala di Penrose!
Alunno 01: Sì, non mi è uscita benissimo, però sono riuscita a farla. E guarda cosa succede quando mi avvicino!
Prof.1: Si vede che non è realmente una scala!
Alunno 01: Esatto! Però, vedi? In questa ultima slide, si vede il punto di vista della prima parte.
Prof.1: Ah, eri lì in alto?
Alunno 01: Sì. È solo da quel punto che la scala appare reale!
Prof.1: Ma… non è che per caso hai realizzato anche il Belvedere di Escher?
Alunno 01: Sì. Eccolo qui!
Prof.1: Bellissimo! Sembra proprio reale!
Alunno 01: Sì. E ci si può salire sopra, scoprendo che i due piani sono perpendicolari e scollegati e che la scala che collega i due piani in realtà è come sospesa.
Prof.1: Bellissimo! Davvero un gran bel lavoro! 

La voce si perde, mentre entra Alunno 02: 

Il gioco della PROSPETTIVA

Alunno 02: Buonasera a tutti e benvenuti alla seconda conferenza corale di BergamoScienza! Dopo il successo strepitoso dell’anno scorso (se n’è parlato per settimane nei corridoi della scuola) abbiamo deciso di ripetere l’esperienza. Durante questa serata, vi mostreremo ciò che abbiamo realizzato nei nostri laboratori…
Prof.2: (seduta tra il pubblico) Ma… e la scena di prima? Non spieghi cosa è successo?
Alunno 02: Beh… (imbarazzata) La scena di prima… che dire? Diciamo che si può prestare a diverse interpretazioni, a seconda del punto di vista! Magari è successa davvero da qualche parte – magari quest’estate a casa della Prof.1 – o magari è stato solo un modo per introdurre questa conferenza. Insomma, è davvero difficile stabilire dove stia di casa la verità, così suscettibile ai… punti di vista!

Ma non perdiamo tempo e concentriamoci sul lavoro che dobbiamo fare questa sera! Non vi avevano avvisato? Questa sera vi proponiamo un piccolo gioco, giusto per scaldare un po’ l’atmosfera. Il gioco si intitola: Punti di vista! Vi mostreremo delle fotografie e voi dovrete indovinare di cosa si tratta! Pronti? Basta alzare la mano per rispondere.
Ecco la prima. Che cos’è? 

Diverse voci si alzano dal pubblico: chi dice un pupazzo, chi parla di una rana (!)… 

Prof.3: (sbracciandosi) Io lo so, io lo so, io lo so!
Alunno 02: (sottovoce, fingendo di parlare solo con la Prof.3) Certo professoressa, che lo sa: mi ha aiutato lei a trovarla!
Prof.3: (facendo finta di nulla) È un portasapone!
Alunno 02: Ehm… sì! Bravissima! Passiamo alla seconda immagine allora! Cos’è questo?

Diverse voci si alzano dal pubblico: qualcuno dice sia Batman, qualcuno parla di un pupazzo… 

Prof.3: (sbracciandosi) Io lo so, io lo so, io lo so!
Alunno 02: (sottovoce, fingendo di parlare solo con la Prof.3) Certo professoressa, però, per favore, non risponda lei: è bene che partecipino gli altri!
Prof.3: (facendo finta di nulla) È un apribottiglie!
Alunno 02: Ehm… sì! Bravissima! Sembra proprio che le sapesse in anticipo, eh? Ma allora vediamo se sa cos’è questo!
Questo non lo conosce! Per forza! L’ho inserito senza che lei lo sapesse. Qualcuno sa cos’è? 

Diverse voci si alzano dal pubblico: qualcuno dice sia una pianta, qualcuno una rana (!) e poi: 

Alunno 03: È uno scopino del water! Anzi: è meglio noto con il nome di Merdolino!
Alunno 02: Esatto! Bravissimo! E… questo?
Prof.3: (sbracciandosi) Io lo so, io lo so, io lo so!
Prof.2: (infastidita) Sì, Prof.3, lo sappiamo anche noi! Ma non per questo ci agitiamo come fai tu e diciamo a tutti che è un portauovo! Basta adesso!
Prof.3: Ma così l’hai detto tu! E non hai nemmeno alzato la mano!
Prof.2: Boh, è vero! (e ride)
Alunno 02: (seccata) Beh, direi che questo gioco di riscaldamento non ha funzionato molto.

Allora, passiamo a cose un po’ più serie e lasciamo la parola ai due seri del gruppo, che ci raccontano la prospettiva da un punto di vista molto particolare. Vi presento il Prof.4 e Alunno 03, studente del liceo scientifico. 

La PROSPETTIVA in matematica

Prof.4: Buonasera a tutti. Ora, con Alunno 03, ripasseremo il laboratorio sulla proiezione stereografica che abbiamo presentato alle elementari, perciò, anche se parleremo di matematica, state tranquilli: è davvero semplice!
Alunno 03: Ma certo, è talmente semplice che avremmo potuto presentarlo anche all’asilo.
Prof.4: Ok, allora... anche se non ce ne sarebbe bisogno, spiega un attimo al nostro pubblico cosa sta vedendo in questo momento sulla slide.
Prof.3: LA PROIEZIONE STEREOGRAFICA!!!
Alunno 03: Ma sì, lo sappiamo che per noi è ovvio, visto che ne abbiamo parlato alle elementari... Cerchiamo di stare concentrati e prendiamo la 2-sfera che tutti conosciamo, con il suo bel polo Nord N, di coordinate (0; 0; 1). Consideriamo poi un punto P, di coordinate generiche (x'₁; x'₂; x'₃) appartenente a S² privata di N. Per dedurre l’immagine P’ mediante la proiezione stereografica sul piano z=0, come evidente dalla figura, bisogna determinare l’intersezione della retta NP con xy.
Prof.4: Con calcoli banali troviamo che le equazioni di NP sono (x₁-0)/(x’₁-0)=(x₂-0)/(x’₂-0)=(x₃-1)/(x’₃-1), quindi ponendo x₃=0, ricaviamo le coordinate di P’: (x’₁/(1-x’₃); x’₂/(1-x’₃)), da cui l’azione della proiezione stereografica π_N che tutti conosciamo. (tra il pubblico si sente un po’ di fermento e il Prof.4 si gira, stizzito, facendo segno alle ragazze di fare silenzio)
Alunno 03: E per dimostrare che è una mappa biunivoca tra  e il piano basta ora considerare il viceversa: sia, quindi,  un generico punto di R²... (Le chiacchiere del pubblico aumentano di volume e…)
Prof.4: Alunno 05, per favore, potresti smettere di chiacchierare? Stai disturbando la nostra lezione!
Alunno 05: Mi scusi, prof, non avevo capito che si trattava di una lezione, ma: penso che stiate esagerando!
Prof.4: (infastidito) Cosa intendi, scusa?
Alunno 05: Scusi, non volevo farla arrabbiare, ma intendo che, secondo me, c’è un modo più semplice per spiegare queste cose!
Prof.4: Ah sì! Beh, questo è il tuo punto di vista! (rivolgendosi a Alunno 03, con sarcasmo) A questo punto direi che possiamo lasciare spazio a Alunno 05, allora, visto che ritiene di poter far meglio di noi. Prego, Alunno 05! Procedi!

(Alunno 05 sale sul palco, un po’ imbarazzata) 

PROSPETTIVA e geografia

Alunno 05: Scusate, non volevo essere presuntuosa, ma credo che queste cose si possano spiegare con una certa semplicità, visto che, dopo tutto, le abbiamo spiegate anche ai bambini di quarta elementare durante i laboratori. Voi stavate capendo la spiegazione?
(coro di no, proveniente dal pubblico – aizzato dagli animatori presenti)
Ok, allora provo io a spiegarvelo, che ne dite?
Sappiamo tutti che possiamo rappresentare la superficie della Terra, che è rappresentabile con una sfera.
Prof.4: UN GEOIDE!
Alunno 05: Sì, ehm, si può approssimare con una sfera, non abbiamo parlato di geoidi con i bambini delle elementari. (Alunno 03 e il Prof.4 lasciano il palco, infastiditi) Comunque, possiamo rappresentare la superficie della Terra con i paralleli, circonferenze parallele all’Equatore, e i meridiani, le circonferenze massime passanti per i Poli, e questo permette di realizzare un reticolo, che possiamo riportare su un foglio per rappresentare i continenti. Ovviamente una carta piana non può riportare precisamente ciò che si trova su una sfera: pensate ad un’arancia! Qualcuno è mai riuscito ad appiattire completamente la buccia intera di un’arancia? No! Non è possibile! (e, come dimostrazione, sbuccia un’arancia e cerca di appiattirne la buccia). Perciò, una carta geografica “piatta” non può che essere un’approssimazione di ciò che si trova sulla sfera.

Procediamo a realizzare la nostra carta geografica, come abbiamo fatto con i bambini delle elementari. Prendiamo come riferimento l’Equatore, che evidenziamo sulla carta, e un meridiano a caso (nel caso della Terra si usa il meridiano di Greenwich): questi costituiscono i nostri assi cartesiani sul foglio. Contando i meridiani e i paralleli, possiamo ottenere le coordinate dei vertici della figura rappresentata su questa sfera e, unendoli, rappresenteremo il “continente” anche sulla nostra carta. Partiamo dall’origine e scegliamo il primo punto del nostro continente a forma di M: ci spostiamo verso destra di 2 unità e verso il basso di altre 2 unità e rappresentiamo questo punto sul piano. Procediamo con il secondo punto, che si trova 4 unità lungo il meridiano andando verso il polo Nord e facciamo la stessa cosa con tutti gli altri vertici della nostra M.

Quella che ho usato per questa proiezione è la carta di Lambert, che, come possiamo vedere dagli indicatori di deformazione di Tissot, conserva le aree dei continenti, ma non le loro forme. Infatti, le circonferenze rappresentate diventano ellissi avvicinandosi ai Poli, ma mantengono la stessa area. Al contrario, la proiezione di Tolomeo, che avviene a partire da un Polo e tracciando i raggi che incontrano i punti della semisfera opposta e li proiettano su un piano parallelo all’Equatore ma passante per l’altro Polo, conserva le forme, e quindi gli angoli, ma non le aree, infatti le forme restano sempre circolari, ma aumentano la propria area allontanandosi dai Poli. Infine, la carta forse più nota è quella di Mercatore, che non conserva l’area, ma l’ampiezza degli angoli e per questo motivo era la preferita dai navigatori.

(Alunno 05, presa dalla spiegazione, decide di andare anche oltre)

Alunno 05: Sapete, durante i laboratori non abbiamo parlato solo di carte geografiche, ma anche di stelle e credo che potrebbe spiegarvele molto bene il mio collega Alunno 06. Alunno 06 (chiamandolo dal pubblico), puoi proseguire tu? 

La PROSPETTIVA delle stelle

Alunno 06: (salendo sul palco) Grazie, Alunno 05, per questa occasione. Io direi, però, che potremmo parlare delle stelle come avremmo voluto fare fin dall’inizio. Ricordi al campus quando avevamo parlato degli oroscopi, ma i professori hanno detto che non avrebbe funzionato durante i laboratori? Io direi che, visto che con le stelle abbiamo avuto un grande successo, potremmo cominciare proprio dall’oroscopo. Però lo facciamo in modo un po’ originale! Allora… Visto che io sono del segno del toro, comincerei proprio dalla costellazione del Toro e leggerei l’oroscopo di oggi per me (alle sue spalle compare l’immagine della costellazione del Toro allo specchio ma lui non se ne accorge, troppo intento a frugare in tasca alla ricerca dell’oroscopo del giorno…)
“La giornata del toro non avrà grandi eventi di rilievo” – (commenta con Alunno 05) vero! Non è successo niente di che, oggi
Alunno 05: Infatti, siamo stati qui tutto il giorno a fare le prove!
Alunno 06: (proseguendo nella lettura) “ma in serata avrà l’occasione di sentirsi al di sopra di tutti” – ed effettivamente sono qui su un palco, più in alto di tutti voi! – “Peccato che questa sensazione di forza sarà in qualche modo smorzata dall’amore” – Perché? Con Alunno 07 va tutto bene…
Alunno 05: Non avete litigato?
Alunno 06: No, va tutto bene! Comunque, l’oroscopo si conclude con: “Il vostro partner vi riporterà con i piedi per terra!” – Chissà che significa…
(Alunno 06 non fa a tempo a finire la frase, che una inviperita Alunno 07 lo tira giù dal palco e, cercando di non farsi sentire dal pubblico, sibila):
Alunno 07: Ma sei impazzito? Cosa stai facendo? Va bene che assomigli a Paolo Fox, ma mi pare che tu stia esagerando!
Alunno 06: Ma è una cosa del campus. Tu non c’eri, non puoi saperlo!
Alunno 07: Però so che non si può parlare di oroscopi durante un festival scientifico! Facciamo così, lascia perdere questa storia degli oroscopi e facciamo vedere l’attività delle stelle, dai! (Lo riporta sul palco e poi si rivolge al pubblico) Magari potremmo far partecipare al nostro gioco qualcuno del pubblico, per far vedere come funziona la nostra attività sulle stelle, che ne dici?
Alunno 06: Hai ragione! (Sale sul palco uno degli animatori dell’anno scorso)
Alunno 07: Dopo tanti anni da animatore, una volta tanto fai l’animato! 

Alunno 06 e Alunno 07 presentano l’attività, mentre ExAlunno 08 deve realizzare quanto richiesto 

Come vedi, ExAlunno 08, all’interno della scatola abbiamo realizzato la costellazione della bilancia (Alunno 07 accende la torcia del cellulare, per illuminare l’interno della scatola, ExAlunno 08 si inchina a guardare all’interno). Se, però, giriamo la scatola e mostriamo il piano laterale della nostra scatola, vediamo che non compare più la costellazione, come l’avevamo vista all’inizio. Sai dare una spiegazione?
ExAlunno 08: Beh, perché girando la scatola ho un diverso punto di vista!
Alunno 06: Esattamente! E proprio questo ci ha permesso di far capire ai partecipanti ai nostri laboratori che le costellazioni non esistono realmente, sono delle illusioni!
Alunno 02: Volete parlare di illusioni? Allora tocca a me…
(Alunno 02 fa per alzarsi, ma Alunno 09 la trattiene e le sibila) Non tocca a te, ora!
Alunno 02: Non tocca a me? Sei sicura?
Alunno 09: Sicurissima
Alunno 06: (riprendendo a parlare come se non fosse stato interrotto) Credo che sia chiaro per tutti come funziona questa storia delle costellazioni. Anche la visione di una costellazione dipende dal punto di vista e quelle che noi “leggiamo” nella volta celeste sono frutto della nostra posizione e, in altre parole… (Tra il pubblico, Alunno 10 ed Alunno 11 cominciano a parlottare, interrompendo la spiegazione di Alunno 06) Alunno 10, Alunno 11, non potreste stare un po’ zitte? Qui stiamo cercando di lavorare!
Alunno 10: Alunno 06, stavo solo dicendo a Alunno 11 che, secondo me, quello che abbiamo fatto nel laboratorio di arte potrebbe essere più semplice per spiegare la prospettiva. Se vuoi, possiamo andare a prendere una cosa nella sala della mostra e te la facciamo vedere. (Senza aspettare una risposta, si alzano ed escono)
Alunno 06 (rivolto a Alunno 07): Ma tu sai di cosa stanno parlando?
(Alunno 07 scuote la testa. Rientrano Alunno 10 ed Alunno 11 e salgono sul palco) 

PROSPETTIVA meccanica

Alunno 11: Stavo raccontando a Alunno 10 che durante la mostra, abbiamo usato questo strumento inventato, pensate un po’, da Leonardo da Vinci. Noi l’abbiamo realizzato per la mostra, ma è stato così efficace che anche i bambini più piccoli riuscivano a capirne il funzionamento. Avremmo bisogno, però, di qualcuno del pubblico per spiegarlo meglio e…
(Alunno 12, travestito da Leonardo da Vinci con una vistosa tunica dorata e una parrucca, che lo fa assomigliare più a Einstein che a Leonardo, sale sul palco, inchinandosi di fronte al pubblico. Dal pubblico – sempre aizzato dagli animatori – si levano grida entusiaste. Alunno 11 e Alunno 10 sono un po’ intimidite):
Alunno 10: Buonasera, signor Leonardo! Che piacere averla qui con noi!
(Leonardo-Alunno 12 non parla, si limita a fare cenni con la testa e a sorridere)
Alunno 11: Signor Leonardo, vuol provare a farci vedere come funziona questo strumento di sua invenzione?
(Leonardo-Alunno 12 si siede e, enfatizzando i gesti, comincia a disegnare. Nel frattempo, Alunno 11 e Alunno 10 predispongono un solido dietro la reticella e spiegano al pubblico)
Alunno 10: Vedete, questo strumento è un prospett… un prospett…
(dal pubblico si leva una voce):
Prof.3: PROSPETTOGRAFO!
Alunno 11: Ecco, grazie… Questa, ehm, finestrella! serve per rappresentare con facilità gli oggetti in un disegno, dando un’idea di profondità.
Alunno 10: Sì, Alunno 11, serve per trasferire la realtà tridimensionale su un foglio bidimensionale, usando la prospettiva, senza però aver bisogno di conoscere tutte le regole della prospettiva. In questo modo, si riesce a dare un’idea di profondità e…
(Leonardo-Alunno 12 si alza in piedi e mostra una riproduzione del Cenacolo!)
Alunno 11: Oh… beh… (resta senza parole)
Alunno 10: Beh, direi che non ha proprio esattamente mostrato come funziona, ma… beh, diciamo che ha usato la prospettiva. (voltandosi verso il pubblico) Voi che dite?
(applausi dal pubblico, aizzati dagli animatori. Leonardo-Alunno 12 si inchina e si allontana dal palco compiaciuto)
Alunno 11: Beh… (imbarazzata) direi che abbiamo fatto ciò che volevamo, ma mi ero illusa che…
Alunno 02: Volete parlare di illusioni? Allora tocca a me…
(Alunno 02 fa per alzarsi, ma Alunno 09 la trattiene e le sibila) Non tocca a te, ora!
Alunno 02: Non tocca a me? Ma a chi tocca allora?
(dal pubblico si leva una voce):
Prof.3: alla Prof.5!
(La Prof.5 si alza in tutta fretta e si avvicina al palco) 

PROSPETTIVA chimica

Prof.5: Buonasera a tutti! Scusate, mi sono distratta un attimo! È che i ragazzi sono così bravi che si resta rapiti ad ascoltarli, non trovate? Allora, io sono un’insegnante di scienze, ma sono innanzi tutto una chimica e, quindi, vorrei parlarvi di chimica. Sapete, quando abbiamo progettato questi laboratori di BergamoScienza, noi docenti di scienze avevamo grandi idee e avremmo voluto parlare di tante cose, ma i ragazzi… beh, sapete come sono fatti i ragazzi! Hanno detto che, siccome toccava a loro fare i laboratori, avrebbero scelto loro di cosa parlare e, quindi, abbiamo dovuto rinunciare alla bellissima storia di… Rosalind Franklin!

(Alunno 13, impersonando Rosalind, sale sul palco con passo elegante e si inchina al pubblico)

Sapete chi è Rosalind Franklin? È stata una chimica, biochimica e cristallografa britannica e il suo lavoro è stato fondamentale per capire la struttura del DNA… Mi pare importante raccontarvi la sua storia! (Prendendo in mano il libro in inglese su Rosalind Franklin, la Prof.5 finge di tradurre) Sapete, ho appena fatto il corso B2, perciò posso permettermi di tradurvi direttamente il testo!

C'era una volta una giovane scienziata di nome Rosalind Franklin. Era molto curiosa e intelligente, e passava le sue giornate in laboratorio, cercando di scoprire i segreti della vita. Un giorno, dopo tanto lavoro e studio, fece una scoperta incredibile. Rosalind era felice, ma anche concentrata. Sapeva di avere qualcosa di grande tra le mani, ma non immaginava che due loschi scienziati, Watson e Crick, stessero osservando da lontano, pronti a prendersi il merito di quella scoperta. Senza che lei lo sapesse, rubarono la famosa ‘Foto 51’. Con quell’immagine, Watson e Crick capirono come era fatta la struttura del DNA. Svelarono al mondo la loro scoperta, e furono acclamati come eroi. Ma nessuno sapeva che, in realtà, il loro grande successo era anche merito di Rosalind.

(Mentre la prof.5 racconta, Rosalind-Alunno 13 guarda nel microscopio, poi ad un certo punto ne tira fuori una fotografia e la osserva. Nel frattempo, Watson-Alunno 14 e Crick-Alunno 15, la guardano scuotendo la testa, commentando tra loro con aria sarcastica. Quando Rosalind-Alunno 13 mette la foto nella borsa, Watson-Alunno 14 e Crick-Alunno 15, le rubano la borsa. Poi si vedono esultanti mentre ricevono il premio Nobel consegnato da Alunno 10. Ad un certo punto, Watson-Alunno 14 prende la parola):

Watson-Alunno 14: (parlando con accento inglese) Vorrei raccontarvi la mia versione della storia, o meglio la versione ufficiale, e non ho bisogno di spendere troppe parole. La verità è che Rosalind non aveva davvero capito quale sarebbe stata la struttura del DNA. Ha fatto semplicemente una buona fotografia, tutto qui, ma non era in grado di interpretarla. Vorrei farvi vedere cosa abbiamo intuito io e Crick e, casualmente, ho qui una piccola realizzazione tridimensionale di ciò che intendo. (Alunno 14 mostra al pubblico la sua riproduzione di un modello del DNA e alle sue spalle compare l’immagine di come abbia funzionato la fotografia, mostrata durante un laboratorio dai nostri animatori). Quella di aver capito davvero la struttura del DNA era, per Rosalind, solo una vana illusione…

Alunno 02: Volete parlare di illusioni? Allora tocca a me…
(Alunno 02 fa per alzarsi, ma Alunno 09 la trattiene e le sibila) Non tocca a te, ora! 

Illusioni PROSPETTICHE

Alunno 02: Non tocca a me? Ma… Le illusioni sono belle, devo parlarne io! (Sale sul palco e comincia a mostrare delle illusioni sullo schermo). Allora: è il momento di parlare delle illusioni ottiche. Sapete, no, quando il cervello male interpreta ciò che vedono gli occhi? Ecco, ora vediamo se voi riuscite a vincere il vostro cervello. Ecco la prima illusione: secondo voi, qual è la linea più lunga tra queste due in neretto?
Alunno 09 (dal pubblico, esasperata): sono uguali, è evidente!
Alunno 02: Ma, veramente, non è così evidente, comunque… passiamo alla prossima:
Alunno 09 (dal pubblico, esasperata): i due tavoli sono uguali!
Alunno 02: Ma io non avevo ancora chiesto niente. Ma Alunno 09, insomma, smettila, non puoi far sempre così
Alunno 09 (dal pubblico): Ma smettila tu, scusa!
Prof.2 (dal pubblico), facciamo che smettete entrambe? Anzi (alzandosi e andando verso il palco, e rivolgendosi al pubblico), io direi che si è fatta una certa e che potremmo anche chiudere qui…
Prof.1 (dal pubblico): NO!
Prof.2: Come scusa?
Prof.1 (dal pubblico): Ci sono ancora 212 slide da mostrare, non si può chiudere così! Alunno 16, prof.6, non dovevate parlare delle vostre proiezioni?
(Alunno 16 e prof.6 si alzano dal proprio posto tra il pubblico e raggiungono il palco)

PROSPETTIVA anamorfica

Prof.6: Direi che non si può chiudere la conferenza senza parlare dell’anamorfosi!
Alunno 07: Oh, che bello, professoressa, l’ha pronunciato alla greca! Si vede proprio che è una grecista!
Prof.6: Grazie, Alunno 07. Dicevamo, Alunno 16, che ne dici di parlare di anamorfosi?
Alunno 16: Sono d’accordo! Soprattutto dopo che ho passato un intero pomeriggio, con la prof.7, a capire come colorare quelle benedette griglie!
Prof.6: Sì, certo, ma soprattutto dobbiamo parlarne perché sono davvero belle. Sai, ad esempio, che sono state fondamentali per realizzare la Cappella Sistina?
Alunno 16: No, guardi professoressa che si confonde: l’anamorfosi è quella che abbiamo fatto con le griglie quelle rotonde
Prof.6: Intendi le griglie polari?
Alunno 16: Sì, certo… non ho detto polari?
Prof.6: No, comunque l’anamorfosi è quella deformazione che Michelangelo ha dovuto usare per rappresentare le figure umane più in alto nella Cappella Sistina, altrimenti per un effetto prospettico noi…
Alunno 16: Sì, va bene, è interessante, ma forse è meglio se presentiamo quello che abbiamo fatto con i bambini delle elementari, no? Così almeno capiscono tutti!
Prof.6: Va bene, come vuoi tu.
Alunno 16: (mostrando l’immagine di un disegno realizzato su una griglia polare) Ad esempio questo: secondo lei cosa rappresenta?
Prof.6: Eh… io direi: chiediamolo al pubblico! Però… prof.3, per favore, non dare tu la risposta, ok? Lasciamo che ci provino loro!
(Tentativi da parte del pubblico e poi…)
Alunno 16: C’è un trucco per capire cosa è rappresentato! Basta usare uno specchio cilindrico…
Prof.6: Sì, direi che così è più chiaro (mostrando la fotografia della griglia polare riflessa da uno specchio cilindrico). Certo che l’idea di rappresentare un cuore con occhi e bocca…
Alunno 16: Proviamo con questo, allora! Che cos’è? (e mostra una seconda griglia polare)
(Tentativi da parte del pubblico e poi…)
Alunno 16: Lo so, lo so, quel cappello sembrava un colletto, vero? E invece no! L’immagine è capovolta!
Prof.6: Ma così, Alunno 16, hai svelato il trucco. Ora non funzionerà più…
Alunno 16: Secondo me non è così semplice, nemmeno conoscendo il trucco. Proviamo! Cos’è questo?
(Tentativi da parte del pubblico e poi…)
Prof.6: Questo effettivamente non è semplice, nemmeno a sapere che devi guardarlo a testa in giù. Proviamo a girarlo (l’immagine viene capovolta)
Prof.6: Così dovrebbe essere più chiaro…
Alunno 16: Certo, sì! Ed è… (rivolgendosi al pubblico… e…)
Prof.3: UN CUORE! Scusate, non ho resistito, ma era così semplice!
Alunno 16: Semplice, certo!
Prof.6: Alunno 16, siccome non abbiamo la foto sullo specchio, potremmo invitare qualcuno del pubblico perché verifichi se è davvero un cuore, no? (Rientra Leonardo-Alunno 12)
Alunno 16: Ecco, nessuno meglio di Leonardo può verificarlo visto che pare che anche lui abbia realizzato delle anamorfosi. (Leonardo-Alunno 12 controlla il riflesso, osserva l’immagine proiettata, ci pensa un attimo, guarda di nuovo il riflesso e poi, convinto, alza i pollici)
Prof.6: Direi che se anche Leonardo ha confermato, possiamo dirci soddisfatti e potremmo anche concludere, no? Prof.1, vuoi concludere tu?

Prof.1: (salendo sul palco) Direi che possiamo davvero chiudere qui. Abbiamo parlato di tutto quello che abbiamo presentato nei nostri due laboratori: nel primo, abbiamo fatto un percorso matematico-artistico, che è stato presentato proprio in questa sala, parlando di anamorfosi e mostrando la finestrella prospettica.

Prof.3: PROSPETTOGRAFO!

Prof.1: Sì, certo, prospettografo… o finestrella prospettica! E comunque il nome non cambia la sostanza… ma in ogni modo, stavo concludendo (guardando storto la Prof.3). Le attività che abbiamo svolto nel laboratorio di scienze, invece, avevano per oggetto le carte geografiche, le costellazioni e gli inganni prospettici. Forse stasera abbiamo parlato in modo un po’, diciamo così, originale di queste cose e forse avete ritenuto che siamo stati un po’… sopra le righe, ecco! In tal caso, forse sarebbe meglio rendersi conto che questa non è stata una vera conferenza, ma una… come dire?... illusione?!?!

Alunno 02: Illusione! Ha parlato di illusione! Tocca ancora a me, allora
(Alunno 02 fa per alzarsi, Alunno 09 comincia a tirare fuori un sacco di fogli, quelli usati nel laboratorio)
Alunno 09: Alunno 02, basta! Sono qui le tue illusioni, vedi? E le conoscono tutte tutti! Ora basta, vieni con me che usciamo!
Alunno 02: Ma io…
Alunno 09: Basta, Alunno 02, andiamo che è tardi! (e la accompagna fuori, mentre, parlando sottovoce, ma facendosi sentire dal pubblico): Tra la palla pelosa l’anno scorso e le illusioni quest’anno, hai fatto proprio una pessima figura!

Prof.1: Ecco, sì! È tardi! Perciò non mi resta che ringraziarvi per la vostra presenza, sperando che vi siate divertiti. Noi, nel caso non si fosse notato, ci siamo divertiti un sacco! Buona serata!

Realizzato con il contributo di Carolina Bergamini, Chiara Bertoni, Asia Corna, Francesco Mognetti, Roberta Moretti e dei ragazzi che hanno partecipato ai laboratori di Arte-Matica realizzati presso il nostro istituto, per partecipare al festival di BergamoScienza, Chiara, Rossana, Davide, Luca, Alessio, Luca, Agata, Federica, Nicole, Emma, Lorenzo, Beatrice ed Elisa. L’articolo è la trascrizione (quasi) fedele della conferenza presentata al pubblico venerdì 11 ottobre, nella Sala degli Affreschi dell’Accademia Tadini. Grazie al curatore dott. Marco Albertario per l’ospitalità e per le idee, sparse qua e là, grazie alle quali è stata realizzata la mostra presentata nel corso del Festival. 

In allegato le slide realizzate per l'occasione

“Canta canta, il merlo, il merlo tra i cespugli”
(poesia gaussiana)

Benvenuti all’edizione numero 180 del Carnevale della matematica!

Come i precedenti, il numero 180 è introdotto dalla consueta CELLULA MELODICA predisposta da Dioniso Dionisi che l’ha definita una «cellula melodica con un’armonizzazione minimalista». 

180 è, evidentemente, un numero pari, e, come evidenziato dalla poesia gaussiana sopra riportata ha cinque fattori primi: 2 (che corrisponde a “canta”), 3 (che corrisponde a “il merlo”) e 5 (che corrisponde a “tra i cespugli”). Le ripetizioni della cellula melodica (e la fattorizzazione imparata alla scuola secondaria di primo grado!) ci fanno dire che 180 è dato da 2x2x3x3x5. La somma dei suoi divisori (sono 18) è 366, perciò 180 è un numero abbondante, ma è anche l’undicesimo numero altamente composto, che significa che ha più divisori di tutti i numeri che lo precedono (il prossimo sarà 240). Tra le curiosità a mio avviso più belle che emergono dal web cercando 180:

• è un numero di Harshad nel sistema numerico decimale, cioè è divisibile per la somma delle sue cifre. La definizione di questo numero risale al matematico indiano Dattaraya Ramchandra Kaprekar (1905-1986): lavorò come insegnante per tutta la sua carriera, ma pubblicò diversi articoli di matematica ricreativa. Secondo Wikipedia, il termine Harshad deriva dal sanscrito “harṣa” che significa “grande gioia”;
• è la somma di sei numeri primi consecutivi: 180 = 19 +23 + 29 + 31 + 37 + 41;

• è il numero che indica alcune strade negli Stati Uniti, ma a me piace ricordare la Interstate 180 dell’Illinois, che va da Princeton a Hennepin, per un totale di poco più di 21 km (anche se non è la Princeton che tutti conosciamo, quella della famosa Università e di Einstein, che è nel New Jersey);
• la Vespa 180 Rally della Piaggio è stata prodotta tra il 1968 e il 1973 in 26.000 esemplari

Visto che mi sto perdendo in campo automobilistico, non posso non citare l’«inversione a U», che può essere indicata come una svolta di 180°. È abbastanza comune, quando si nomina 180, pensare all’angolo piatto, indicato in radianti come p, e direi quindi che è il caso di passare al primo post (che non è esattamente in tema, ma a suo modo sì), che tratta della Sezione Aurea e di un’identità dove compaiono contemporaneamente alcune delle più importanti costanti matematiche. Essendo formule che contengono Pi Greco, ecco trovata la prima connessione con il #180. Il post è di Mauro Merlotti dello Zibaldone Scientifico e si intitola Formule complesse. 

Il tema scelto per questa 180^ edizione del carnevale è Matematica e sport, ispirato da questa estate di Olimpiadi e Paralimpiadi, da un mondo dello sport sempre più ricco di matematica e da una matematica che può offrire sempre più risorse anche allo sport.
Comincio il Carnevale settembrino dando la precedenza ai matematti che hanno scritto qualcosa in tema. La prima a rispondere alla chiamata è stata Annalisa Santi, che ha dedicato il proprio contributo al grande campione Francesco Molinari, l’uomo che il 22 luglio 2018 entrò nella storia del golf. «Con questo articolo avevo voluto fare un omaggio al grande golfista che vinse l’Open Championship scozzese, il più antico e celebre dei Major, lasciando così a Carnoustie, per la prima volta dal 1860, il nome di un atleta italiano, e, nello stesso tempo, parlare di questo stupendo gioco del golf e di un po’ della matematica che vi si cela.»

Mauro Merlotti, dalle pagine dello Zibaldone scientifico, parla del fotofinish, uno «strumento indispensabile per molte gare sportive; potrebbe sembrare una fotografia, ma mentre questa è la riproduzione un oggetto ad un determinato istante (almeno in prima approssimazione), il fotofinish riproduce un oggetto ad una determinata posizione (con scorrimento continuo della pellicola)».

Nel suo blog Gli studenti di oggi, Roberto Zanasi propone un post senza tante parole, con un grafico della classifica delle Olimpiadi costruito con «un ordinamento parziale in cui uno stato X è stato migliore di un altro stato Y se il medagliere di Y può essere trasformato nel medagliere di X mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.»

Paolo Alessandrini, autore di Matematica in campo, non poteva far mancare il proprio contributo a questa edizione del Carnevale e infatti ci regala ben sei post, quattro in forma di “shorts” e due in forma di video più lunghi e articolati. I link rimandano al nuovo blog Paolo Alessandrini – Racconto la matematica in più modi: sono autore, divulgatore, docente. Ecco l’elenco dei link, descritto direttamente da Paolo:

1. Dalle origini a EURO 2024: storia e geometria dei palloni da calcio: Un viaggio attraverso l’appassionante storia dei palloni da calcio, con particolare attenzione alle questioni geometriche
2. Eurogoal a effetto: dal cucchiaio di Totti al tiraggiro di Zaccagni: Curiosamente, molti dei più famosi tiri a effetto della nostra Nazionale di calcio sono andati in scena durante edizioni del campionato europeo: ecco la matematica e la fisica che sta dietro queste prodezze.
3. Olimpiadi, che palle! Uno short dedicato ai vari tipi di palla utilizzati nelle specialità olimpiche.
4. La matematica di Marcell Jacobs: Uno short sul teorema di Lagrange applicato ai 100 metri olimpici.
5. La matematica (e la fisica) di Gimbo Tamberi: Uno short sulla matematica e sulla fisica del salto in alto.
6. La formula rivoluzionaria della Champions League 2024-25: Uno short sulla nuova formula della Champions League, molto curiosa dal punto di vista combinatorio.

Per i contributi di MaddMaths! comincio dai due contributi realizzati sulla scia degli ultimi europei di calcio, lasciando a loro la parola:

• EURO 2024: l’europeo dei dati Euro2024 ha visto la vittoria della Spagna in finale contro l’Inghilterra. Oltre che in campo, questo campionato europeo si è giocato tra numeri, algoritmi e dati. Ce ne parla Marco Menale per la rubrica La Lente Matematica.
• Il tabellone ad eliminazione diretta degli Europei: una scelta non ottimale? Sono finite le partite dei gruppi di Euro2024 e sta per iniziare la fase ad eliminazione diretta. Olanda e Austria potrebbero rincontrarsi già ai quarti di finale!! Com’è possibile? È un errore? Cesco Reale (divulgatore ludo-scientifico: ecco la sua divulgazione matematica e quella ludica) e Alberto Saracco provano ad approfondire, per capire meglio come il ragionamento matematico possa portare alla creazione di tornei più equi.

E, poi, un paio di extra sul tema, dall’archivio di questo 2024:

• Marco Menale ha raccontato in tre episodi de La Lente Matematica cos’è l’xG – expected goals, e come questo parametro si colleghi all’angolo di tiro e all’angolo Kos, ossia l’angolo di tiro considerando gli avversari presenti di mezzo.
• Le leggi di Newton aiutano a nuotare meglio Cento anni fa, alle Olimpiadi di Parigi del 1924, l’americano Johnny Weissmuller vinse i 100 metri di stile libero maschili con un tempo di 59 secondi. Quasi un secolo più tardi, nelle Olimpiadi di Tokyo 2020, Caeleb Dressel, sempre nello stesso stile, portò a casa la medaglia d’oro rosicchiando 12 secondi a Weissmuller. I tempi, in questo sport, sono significativamente migliorati negli anni come risultato combinato di diversi fattori di innovazione applicati all’allenamento, alla strategia di recupero, alla nutrizione, nonché all’uso di più moderne attrezzature. Ma un ruolo chiave, in questi progressi, va riconosciuto sicuramente alla biomeccanica della bracciata, che ha consentito di ottimizzare le tecniche natatorie in ogni stile. Negli anni ultimi, l’integrazione di principi matematici e scientifici e l’uso di sensori indossabili ha ulteriormente perfezionato le prestazioni degli atleti, come dimostrano i risultati della squadra di nuoto dell’Università della Virginia (UVA), capitanata dall’allenatore Todd De Sorbo ed assistita da Ken Ono. Ce ne parla Stefano Pisani per le News.

Tra le varie proposte pervenute da Gianluigi Filippelli per il suo blog DropSea, c’è l’articolo Inseguimenti in pista, a tema Formula 1, per la serie dei Paralipomeni di Alice: il problema è proposto da Maurizio Codogno nel 22° volume della serie Matematica della Gazzetta dello Sport ed è una bellissima idea da proporre in classe. Siccome il post è stato pubblicato in occasione del Gran Premio d’Ungheria, Gianluigi si è divertito a cercare le due velocità che permettono le prestazioni riportate nel problema proprio sul circuito d’Ungheria, scoprendo risultati a dir poco fantascientifici, per delle auto da corsa.

I matematti difficilmente riescono a stare nei confini di un tema, forse perché la matematica stessa va ben al di là dei limiti imposti, perciò non sorprende che i contributi di altri argomenti superino di gran lunga quelli che parlano di sport. Procediamo quindi con Dioniso Dionisi, che ci offre la prima parte di Archita, Platone, Eudosso e la duplicazione del cubo. Si tratta, secondo le parole dell’autore, di «un dialogo in cui il giovane Eudosso illustra a Platone, in visita a Taranto, la soluzione del suo maestro Archita per la duplicazione del cubo.» Eccone un estratto: “«Ah, conosco bene la duplicazione del cubo», replicò subito il giovane. «Il maestro Archita ha preteso che la studiassimo a fondo. Anche perché… la vera soluzione è sua. Quella di Ippocrate è insufficiente perché semplifica il problema ma non lo risolve. Invece il mio maestro ha trovato la soluzione concreta e non solo teorica, come quella di Ippocrate». «E… quale sarebbe questa soluzione concreta?», chiese Platone con circospezione.”

I contenuti di Maurizio Codogno sono tantissimi, come sempre. Eccoli, presentati da lui stesso e distinti per categoria.

Cominciamo con i volumi della collana Matematica:

• 19 – L’analisi matematica, di Salvatore Fragapane: risposte a domande che non vi siete mai fatti sul perché si studia analisi.
• 20 – La teoria dell'informazione, di Maurizio Codogno: quante cose ho dovuto ristudiare per scriverlo :-) ma spero di aver dato un’idea del come si può inviare messaggi con alta probabilità di ricezione.
• 21 – Le trasformazioni geometriche, di Bruno Cifra: una visione unificatrice di tutte le geometrie, seguendo il programma di Erlangen.
• 22 – L’algebra, di Paolo Gangemi: le definizioni di base dell’algebra come si studia all’università.
• 23 – I numeri complessi, di Marco Erba e Claudio Sutrini: molto interessante la parte dove si mostra come i numeri complessi siano necessari in fisica quantistica.
• 24 – L’analisi complessa, di Paolo Caressa: vincoli a gogo rendono più interessante la struttura rispetto all’analisi in campo reale.
• 25 – La teoria dei numeri, di Francesco Zerman: uno sguardo su alcune parti della regina della matematica, con parti che non trovate facilmente in giro come quella sui numeri p-adici.
• 26 – Le equazioni differenziali, di Marco Menale: dalla propagazione di un’epidemia a quella del calore, la parte della matematica che più serve alla fisica.
• 27 – La geometria algebrica, di Ottavio G. Rizzo: non arriviamo a risolvere l’Ultimo Teorema di Fermat, ma almeno abbiamo una minima idea del perché si parla di curve ellittiche.
• 28 – La teoria dei grafi, di Sonia Cannas e Ludovico Pernazza. Le basi di una teoria nata con Eulero e sviluppatasi soprattutto con i computer.
• 29 – L’analisi funzionale, di Pierluigi Vellucci: perché mai una funzione deve solo trasformare un numero in un altro numero, e non una funzione in un’altra funzione?
• 30 – La geometria differenziale, di Christian Casalvieri: dopo che l’analisi matematica ha sfruttato la geometria, ora le rende il favore.
• 31 – La matematica dei calendari, dei Rudi Mathematici: usare la matematica in maniera creativa per trovare una quadra dove non c’è.

Ci sono anche altre recensioni matematiche:

• Elogio delle matematiche, di Alain Baidou. Badiou la matematica la sa anche se è filosofo, Losito che l’ha tradotto un po’ meno.
• Dentro l’algoritmo, di Donata Columbro. Ho trovato molto meglio il suo precedente Ti spiego il dato.
• The Golden Ratio, di Mario Livio. Diciamo che ha fatto il possibile col materiale a disposizione.
• La sezione aurea, di Franco Purini: diciamo che non sono riuscito a capire dove si parlasse della sezione aurea.
• The Golden Ratio and Fibonacci Numbers, di Richard A. Dunlap: utile per vedere quali associazioni del rapporto aureo nell’arte sono essenzialmente delle bufale.
• Fibonacci Numbers and The Golden Ratio, tratto da un MOOC su Coursera di Jeffrey Robert Chasnov. Utile solo se non sapete nulla dell’argomento, ma con il vantaggio che il testo è liberamente scaricabile.
• Once Upon a Prime, di Sarah Hart: tante belle chiacchiere – spesso a me ignote – sulla matematica in letteratura.
• The Golden Ratio: The Facts and the Myths, di Francis D. Hauser. Molto minimale, probabilmente troppo.
• The Pleasures of pi, e, and Other Interesting Numbers, di Y. E. O. Adrian: tante formule di serie infinite per i ragazzi.
• Information Theory, Inference and Learning Algorithms, di David J. C. MacKay:come dice il titolo, un approccio non standard alla teoria dell’informazione.

Per quanto riguarda il mercoledì matematico:

• Quando la fattorizzazione non è unica: alcuni esempi di strutture in cui il teorema di fattorizzazione unica è falso.
• Una citazione inutile: alcune considerazioni non tanto sulla prova di matematica all’esame di maturità quanto sulle citazioni nel testo d’esame.
• Le elezioni legislative francesi: partendo dai risultati elettorali francesi (e inglesi) mostro come la matematica applicata al sistema di voto influenzi le scelte.
• Usare equamente una moneta iniqua: approfitto del post per mostrare due tipi completamente diversi di dimostrazione.
• Facile come 1+1: mostro come un sistema di intelligenza artificiale fa una somma modulare. Ufficio complicazione affari semplici.
• Non correte subito a estrapolare!: un esempio di come l’estrapolazione fatta senza pensare può essere peggiore di non dire nulla.
• Che cosa NON È una dimostrazione elegante: racconto quando (per me) una dimostrazione è brutta, anche se funzionante.
• E allora cos’è una dimostrazione elegante?: e poi il mio pensiero su cosa rende elegante una dimostrazione (conta anche l’imprevedibilità)
• Dadi non transitivi: Si possono costruire dei dadi A, B, C dove A in media vince su B, B su C e C su A.
• I dadi di Lake Wobegon: addirittura, si possono costruire dadi A, B, C dove in media ciascuno di essi ha un punteggio migliore della media degli altri due.
• Persi in una foresta: se sai la forma di una foresta ma non dove ti trovi né in che direzione guardi, qual è il percorso da fare per uscire il prima possibile nel caso peggiore?
• Il problema di Brocard: una delle tante congetture di teoria dei numeri che probabilmente non sarà mai dimostrata.

C’è una bella rassegna anche per i Quizzini della domenica:

• Senza conti: si può risolvere… senza conti.
• Quadrato ruotato: ha il bello che può essere risolto in vari modi.
• Multilingue: un’applicazione quasi completa della discesa infinita, con un salto mortale finale.
• Nove punti: chiama a gran voce il principio dei cassetti (e un po’ di geometria di base).
• Quadrante a zig zag: problemino puramente geometrico e pitagorico.
• Piramide numerica: è davvero facile, e la parte più interessante è trovare la soluzione più semplice.
• Batterie scariche: alla fine si è rivelato più complicato del previsto.
• Pesce: a prima vista è impossibile da risolvere, ma alla fine dà un risultato semplice.
• 13-14-15: si può risolvere con la legge dei coseni, ma c’è un sistema più divertente.
• Birra, e sai cosa bevi: abbastanza immediato da risolvere.
• Cioccolatini: per risolverlo ci vuole un po’ di pazienza.
• Tennis non transitivo: in un torneo all’italiana se tutti hanno vinto almeno una partita non c’è un ordine totale tra i giocatori.

Solo un paio di post per la serie povera matematica:

• Perché i maschi non allattano: come è possibile che riviste come Nature pubblichino certi articoli?
• Ognuno ha i suoi modelli: Un sedicente think tank liberale ha messo un post motivazionale: una frase di Unabomber.

È ora dell’altrettanto lunga lista di articoli di MaddMaths! e, come al solito, la parola passa a loro:

• C’è una nuova mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. Nella prima puntata scopriremo cosa studia la topologia partendo da due semplici triangoli. Trovate tutte le puntate su questa pagina.
• Una Intelligenza Artificiale fatta con 21 bicchierini Siete spaventati dall’intelligenza artificiale? Oppure ne siete entusiasti, ma non sapete bene perché? In questo articolo Massimo Ferri, topologo, matematico applicato, ci fa giocare con una versione molto semplificata di “macchina che impara”, mettendo insieme dei... bicchieri. Forse è il modo per capire meglio questa rivoluzione che già sta cambiando le nostre vite.
• Il senso del doppio È uscito il libro “Il senso del doppio – la matematica tra rebus e indovinelli” di Margherita Barile e Giuseppe Pontrelli. Vi proponiamo l’Introduzione del libro.
• Arriva Comunicamat 6 – online dal 9 all’11 ottobre 2024 La sesta edizione del congresso “Comunicare la matematica” ritorna con la stessa formula degli ultimi anni (online su canali dedicati) da mercoledì 9 a venerdì 11 ottobre 2024. Tre pomeriggi a distanza, dedicati a interventi sulla comunicazione e la divulgazione della matematica. Il congresso si può seguire anche come corso di aggiornamento, con iscrizione su SOFIA. Tutte le informazioni su programma, presentazione di ospiti e interventi, iscrizione, partecipazione si trovano sul sito https://comunicamat.unicam.it.
• Matematica e agrivoltaico Il 13 Febbraio di quest’anno è stato pubblicato sul sito del ministero il decreto che “promuove la realizzazione di sistemi agrivoltaici innovativi di natura sperimentale”. Il decreto mette a disposizione risorse per oltre un miliardo di euro con l’obiettivo di realizzare nuovi impianti per un totale di circa 1 GigaWatt (GW). Per comprendere l’entità della misura basti osservare che al 31 Dicembre 2022 la potenza totale installata era di 123 GW, mentre la potenza da fotovoltaico ammontava a 25 GW: si tratta quindi dell’1% circa della potenza totale, e del 4% di quella da fotovoltaico. Ma cosa sono questi “sistemi agrivoltaici”? E cosa c’entra la matematica? Scopriamolo insieme con questo contributo di Annalisa Pascarella dell’IAC-CNR e Alberto Sorrentino dell’Università di Genova, tra le persone fondatrici dello spin-off matematico BEES (bees.srl).
• Un’IA medaglia d’argento alle IMO2024? La notizia non arriva completamente a sorpresa: alcuni segnali, alcune anticipazioni erano nell’aria da alcuni mesi. Ma sapere che un’intelligenza artificiale è riuscita a risolvere correttamente 4 problemi dei 6 dell’ultima Olimpiade Internazionale di Matematica (IMO) fa comunque un certo effetto. Ce ne parla Luigi Amedeo Bianchi.
• Rivoluzioni matematiche: il teorema della palla pelosa di Silvia Benvenuti Con il numero di settembre de Le Scienze troverete in allegato (a 14,90 euro, il prezzo include la rivista) il ventiquattresimo dei trenta volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al teorema della “palla pelosa” ed è stato scritto da Silvia Benvenuti. Mentre, ad agosto è stato il turno dei Teoremi di Shannon a cura di Francesca Carfora.
• Archimede 2/2024: matematica e senso critico Vi proponiamo il sommario del direttore Roberto Natalini del numero 2/2024 della rivista Archimede:

Iniziamo questo secondo numero del 2024 di Archimede con un contributo importante di Anna Baccaglini-Frank, scritto con un gruppo di ricerca internazionale, sull’educazione matematica “tecnocritica”, un approccio che permette agli studenti di «impacchettare e spacchettare la matematica», sia riguardo l’uso della tecnologia digitale in classe sia riguardo l’esplorazione da parte degli studenti della tecnologia che li circonda. Segue la nuova puntata della serie promossa da Francesca Gregorio sui numeri nell’insegnamento con i numeri razionali. Infine Ruggero Pagnan ci propone alcune sfide matematiche che comportano l’esercizio del pensiero laterale. Per le Strane storie matematiche, proponiamo la discussione sul quesito Invalsi sui numeri pari e il lancio di una nuova storia. Il fumetto e la copertina, sempre dedicati a Mandelbrot, sono opera di Lorenzo Palloni, il titolo della storia è “Rugoso”.

• Abbiamo pubblicato un articolo di Daniele Gouthier contenente alcune riflessioni sulla comunicazione della matematica e il suo rapporto con la società. A questo sono seguiti gli interventi di Nicola Ciccoli e Domingo Paola. Si sono, poi, aggiunti Marco Menale con valorizzazione e università e Simone Ramello, dottorando all’ultimo anno presso l’Università di Münster, con il punto dall’estero.
• Risultati INVALSI 2024 in matematica: cosa ci possono dire (o non dire) i primi risultati L’11 luglio 2024 sono stati presentati i risultati delle prove nazionali INVALSI che, tra i mesi di marzo e maggio 2024, hanno coinvolto più due milioni e mezzo di studentesse e studenti italiani appartenenti alle classi II e V della scuola primaria, III della scuola secondaria di primo grado, II e ultimo anno della scuola secondaria di secondo grado. Le studentesse e gli studenti si sono cimentati in prove relative all’Italiano, alla Matematica e all’Inglese (Listening e Reading). Un primo commento di Ketty Savioli della Commissione Italiana per l’Insegnamento della Matematica (UMI-CIIM) sui risultati in matematica.
• Non solo applausi e medagliette – Giornata conclusiva del 31° Rally Matematico Transalpino a Firenze Il primo giugno 2024 si è tenuto a Firenze la 31° edizione del Rally Matematico Transalpino a Firenze. Pubblichiamo un appassionato reportage di un partecipato collettivo di organizzatrici e organizzatori: Brunella Brogi, Fabio Brunelli, Fabiana Ferri, Gianni Gallai, Mirko Marini, Silvia Mazzucco, Ginia Percario, Bice Perna, Chiara Pradella, Francesca Ricci, Valentina Scarpini.

Per La matematica danzante di Raffaella Mulas:

• Pierre de Fermat

Per La Lente Matematica di Marco Menale:

• Probabilità: un pezzo della matematica ingiustamente bistrattato La probabilità può aiutare a comprendere i fenomeni del mondo nella loro complessità, così da evitare pregiudizi e false credenze. Quest’episodio è stato a quattro mani, tra superenalotto e test medici, con Angelo Vulpiani, Professore ordinario di Fisica Teorica alla Sapienza.

Non sarebbe Carnevale se non ci fossero i contributi dei Rudi Matematici ed ecco i “post istituzionali”:

• Chapeau! – Soluzione del quesito di giugno: c’era tutto un discorso parigino che riguardava la sottile capacità di individuare il colore del proprio cappello.
• Tappezzeria formato A8 – Soluzione del quesito di luglio: qui invece tutto il problema sta nello scrivere i numeri naturali tutti attaccati.
• La spiaggia delle meraviglie – Ad agosto, due problemi al prezzo di uno, con il Capo in vacanza che gioca a fare il Cappellaio Matto

I Q&D, invece, sono ben sette e il testo espositivo è così corto che non vale davvero la pena riassumerlo:

• Punti a caso
• Rosso e blu
• Trisezione dell’angolo
• Bicameralismo
• Una cubica
• Posizioni di P
• Ipergioco

Oltre al post in tema Gianluigi Filippelli ha deciso di raccogliere tutti i post estivi in due post: il primo link raccoglie i contributi postati tra giugno e luglio, mentre il secondo raccoglie quelli postati tra luglio e agosto: ci sono le pubblicazioni su DropSea, quelle dal Cappellaio Matto e quelle in inglese, con alcune cose non necessariamente a tema matematico.

Tra gli articoli più recenti ci sono tre recensioni:

• Numeri visti di sbieco di Tommaso Maccacaro e Claudio Tartari
• Il teorema di Pitagora di Paolo Zellini
• Le equazioni differenziali di Marco Menale, 26.mo volume della collana Matematica curata dal “nostro” Maurizio Codogno

Nella sezione de Le grandi domande della vita, invece, ecco Di perimetri, aree e volumi sullo stretto legame analitico tra questi particolari “bordi” geometrici. Infine, dal Caffè del Cappellaio Matto, un post ne La scienza dei supereroi sulla ricorsione: L’Osservatore osserva l’Osservatore che osserva l’Osservatore...

In chiusura, non mi resta che presentare anche il mio articolo Non solo sport: nel quale elenco una serie di caratteristiche necessarie per una buona riuscita nello sport, riconoscendo come siano le stesse per la matematica. Per questo motivo, abbino allo sportivo nel quale ho riconosciuto questa caratteristica un matematico o un fisico, suggerendo letture e spunti di riflessione.

Questo è quanto…

Direi che la rassegna offre, come sempre, matematica per tutti i gusti. Ci si ritrova a ottobre!