Visualizza articoli per tag: circonferenza
Prova parallela matematica terza maggio 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: prova parallela di fine anno sul programma di terza. Geometria analitica: parabola e circonferenza; esponenziali e logaritmi, disequazioni esponenziali e logaritmiche.
Durata: 120 minuti
Prova realizzata in collaborazione con il prof. Francesco Mognetti e la prof.ssa Asia Corna
Cerchi tra i banchi
Si può dire che p sia il protagonista del programma di seconda liceo scientifico: nella prima parte dell’anno scolastico, ci si immerge nell’insieme dei numeri reali e gli irrazionali sono posti al centro della scena. Come dimenticare l’irrazionale per eccellenza?

Nell’immagine è riportata una rappresentazione visiva di alcune cifre decimali di p, 180 per la precisione, che è facile ricostruire assegnando al colore la cifra corrispondente. L’immagine è stata realizzata per uno dei cartelloni esposti durante la seconda partecipazione al Festival di BergamoScienza dell’istituto dove insegno, che ha avuto come protagonista il cerchio.
La classe seconda è il momento in cui si alza il livello di difficoltà: dopo aver risolto equazioni, disequazioni e sistemi lineari, si affrontano, con gli irrazionali nella cassetta degli attrezzi, i problemi di secondo grado ed ecco che in geometria fa la sua comparsa la circonferenza, definita come il luogo geometrico dei punti del piano equidistanti da un punto fisso, il centro.
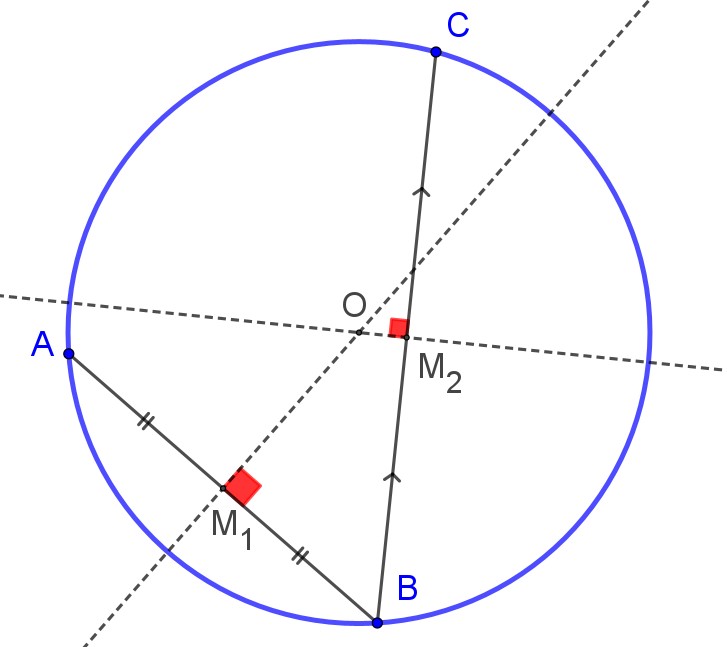
Uno dei primi teoremi che si incontrano riguarda la circonferenza passante per tre punti non allineati, e la dimostrazione permette, in realtà, di fare una semplice costruzione con Geogebra, evitando di usare lo strumento “Circonferenza – tre punti”. Il teorema fa intravedere i teoremi sulle corde, che presto permetteranno di vederne la lunghezza in relazione alla loro distanza dal centro, e di realizzare che davvero l’asse di una corda passa per il centro.
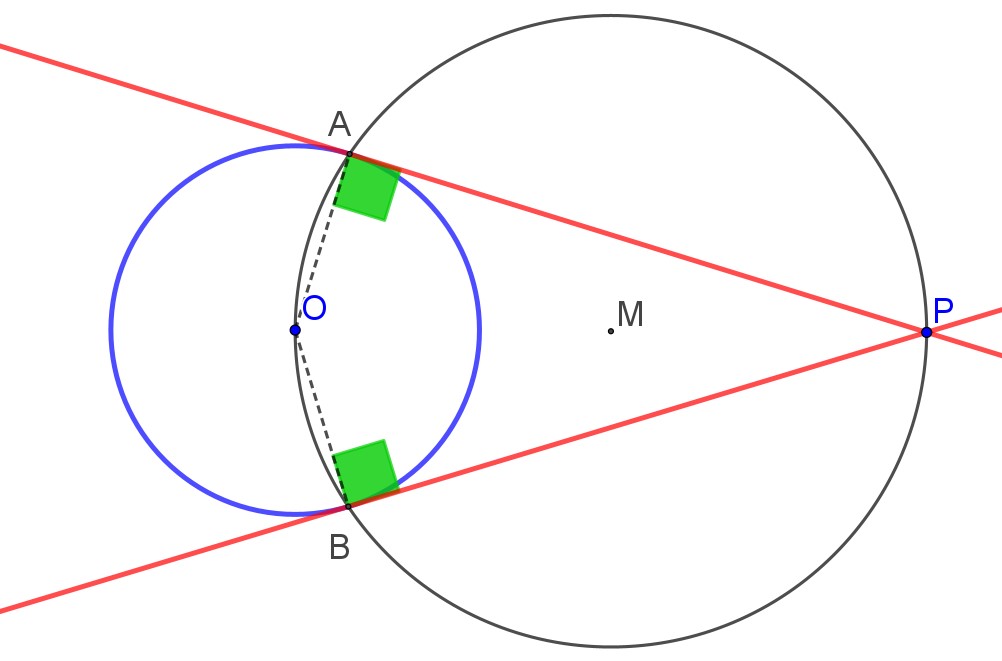
Il passo successivo è quello di considerare le circonferenze in relazione alle rette e, in particolare, in relazione alle tangenti. Così, può capitare di dover imparare a costruire le rette tangenti a una circonferenza tracciate da un punto esterno, basandosi sul fato che una retta tangente a una circonferenza è perpendicolare al raggio passante per il punto di tangenza. Questo risultato ci regala un anticipo sui triangoli rettangoli inscritti in una semicirconferenza.
Il percorso in matematica assomiglia a una danza, con un passo avanti e uno indietro, a creare una coreografia, ritornando su cose già viste, ma affrontandole in maniera diversa, e così nel capitolo successivo le circonferenze incontrano i triangoli, sempre inscrivibili in e circoscrivibili a una circonferenza, ma non solo:
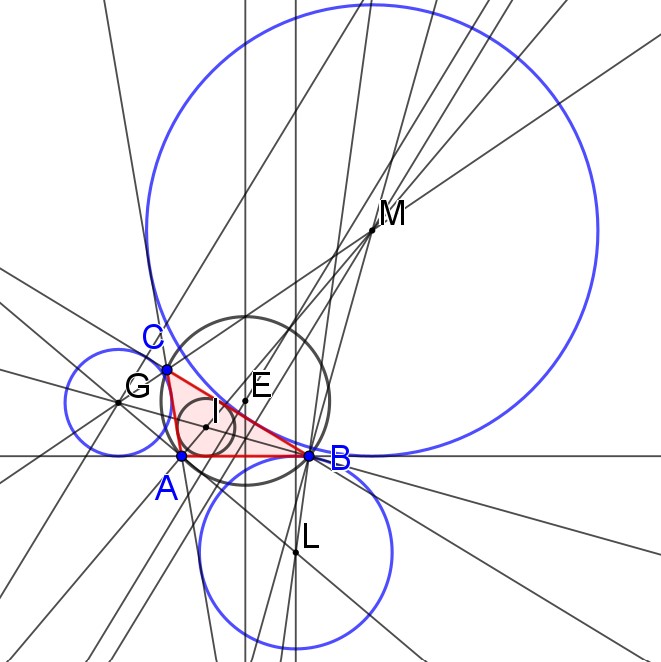
Tra il circocentro (E) come punto di incontro degli assi e centro della circonferenza circoscritta, l’incentro (I) punto di incontro delle bisettrici e centro della circonferenza inscritta, il triangolo ABC incontra anche altre tre circonferenze, di centri rispettivamente M, L e G, detti excentri, punti di incontro della bisettrice dell’angolo interno non adiacente con le bisettrici degli altri due angoli esterni e quelle blu sono le circonferenze exinscritte, tangenti a un lato e al prolungamento degli altri due. È stato vedendo un’opera di Lanfranco Bombelli (1921/2008), pittore, incisore e architetto, che ho pensato a questa rappresentazione e…
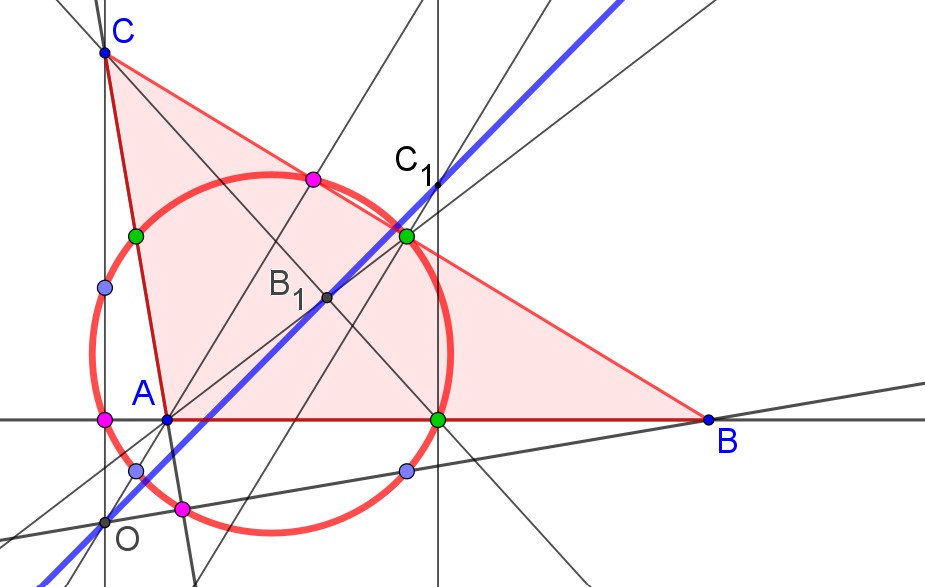
Ripensare al Cerchio per nove punti è stato un attimo: eccola in tutta la sua bellezza! Indicata in rosso passa per tre terne di punti: quelli rappresentati in verde sono i punti medi dei lati del triangolo; quelli in fuxia sono i piedi delle altezze relative ai lati e poi ci sono gli ultimi, più difficili da definire, perché, individuato con O l’ortocentro (il punto di incontro delle altezze di un triangolo), essi sono i punti medi del segmento che ha per estremi O e un vertice del triangolo. Ho scoperto, giusto oggi, che questa circonferenza è nominata come Cerchio di Feuerbach (almeno, stando a quanto dichiarato su Wikipedia), matematico tedesco, fratello del più famoso filosofo. Qualcuno, invece, la nomina come cerchio di Eulero, ma credo che, in questo caso, il celebre matematico potrebbe accontentarsi della paternità della retta, che passa per tre punti notevoli: ortocentro, baricentro, circocentro.
Mentre scorro le pagine del libretto di Bruno Munari intitolato Il cerchio (e scopro ora che ci sono anche Il quadrato e Il triangolo…) dove ho trovato il riferimento a Lanfranco Bombelli, mi imbatto nelle voci “Raggio decrescente” e “Raggio crescente”:
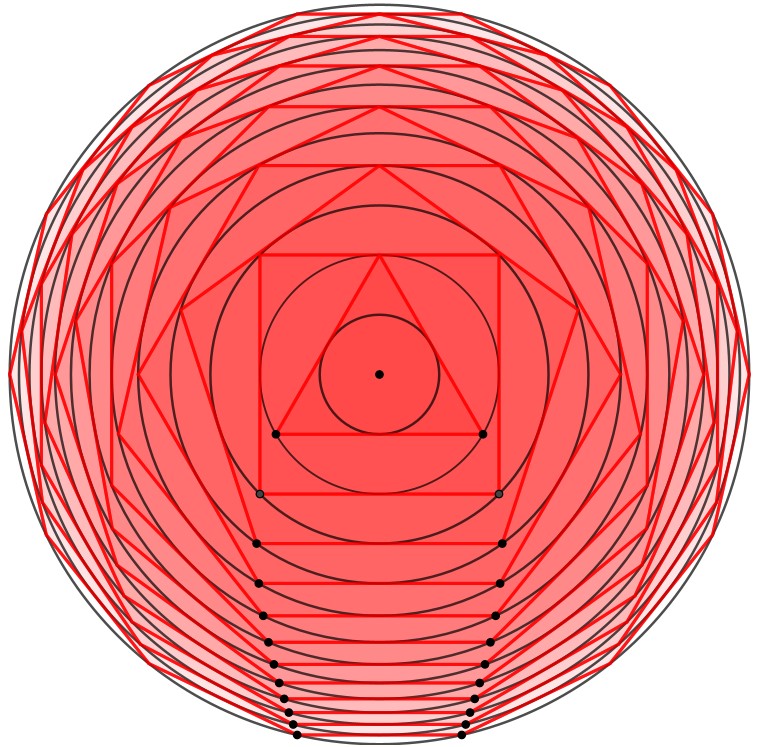
Mi è parso così interessante, che non ho resistito alla tentazione di realizzare quello crescente con Geogebra, arrivando fino al poligono di 14 lati (inventandomi metodi ingegnosi per rappresentare quelli da 7, 9, 11 e 13 lati). Mi piace citare, in particolare, ciò che scrive Munari, oltre alle indicazioni per la costruzione: «Può sembrare che il raggio, aumentando oltre ogni limite, diventi infinito; invece si avvicina a un limite che è circa dodici volte quello del raggio del cerchio primitivo», esattamente come quello decrescente «si avvicina a un limite che è circa un dodicesimo di quello del raggio del cerchio primitivo».
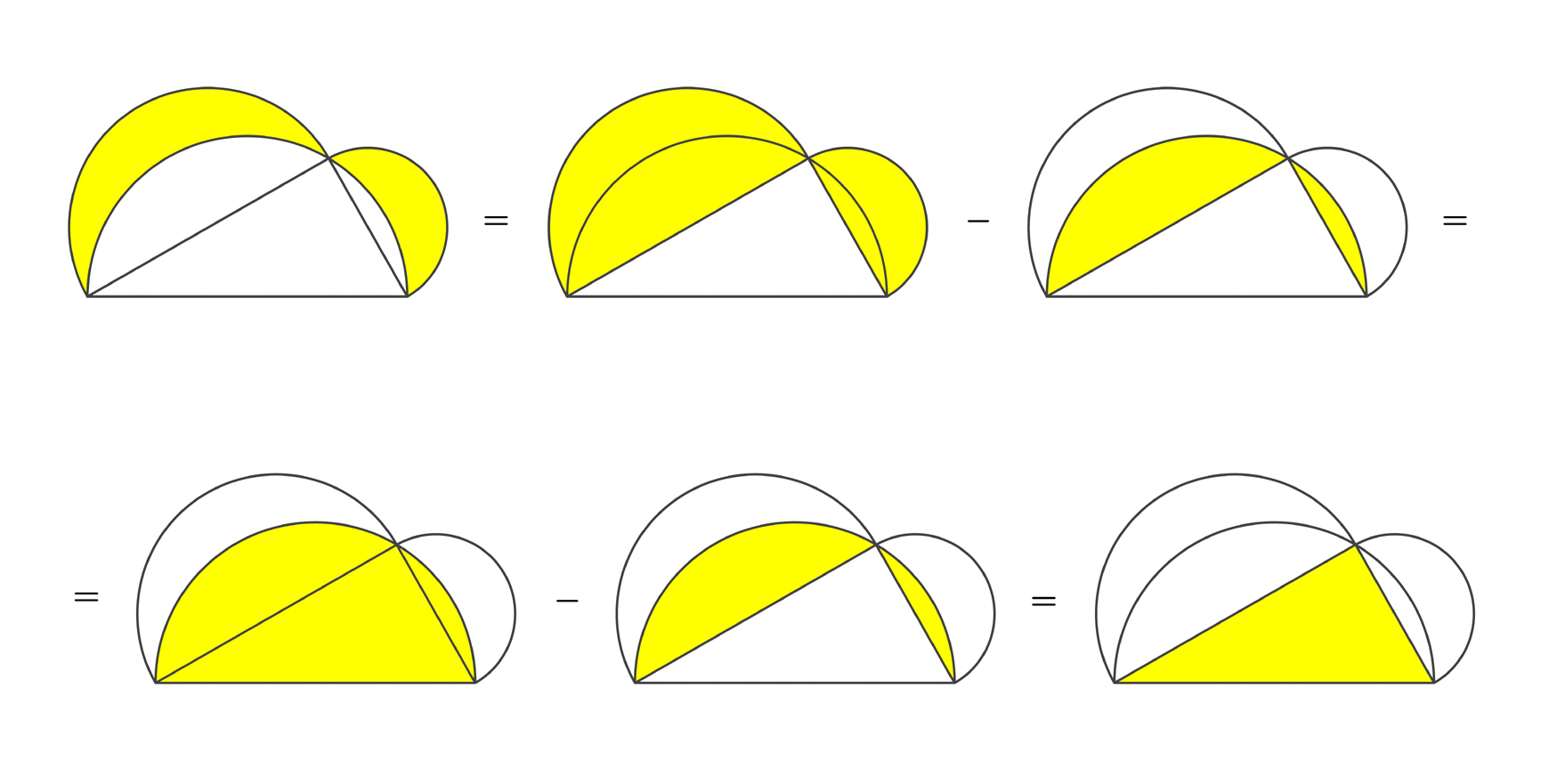
Non ho resistito alla tentazione di riprendere in mano anche questa simpatica dimostrazione senza parole, che utilizza le lunule e il triangolo di Pitagora. Il triangolo rappresentato è rettangolo e ha come lato di appoggio l’ipotenusa. Sui due cateti vengono costruite (e colorate) le lunule, la «parte di piano compresa fra due archi circolari di raggio diverso aventi in comune gli estremi e giacenti dalla stessa parte rispetto alla corda comune». In questo caso, il raggio delle semicirconferenze esterne è pari a metà del cateto e il centro è il punto medio del cateto, mentre l’arco più interno è la semicirconferenza con raggio pari a metà dell’ipotenusa e centro nel punto medio della stessa. La prima differenza è facile, la seconda, invece, ha a che fare con il teorema di Pitagora: come riportato sul sito del Giardino di Archimede, il museo della matematica: «Nell’enunciato del teorema di Pitagora, i quadrati possono essere sostituiti da altre figure, come ad esempio triangoli, esagoni, o anche figure irregolari, purché simili tra loro». Chi ha avuto modo di visitare il museo, avrà provato a mettersi alla prova con i diversi puzzle realizzati proprio con questo teorema di Pitagora generalizzato.
Sul sito, troviamo poi il caso particolare delle lunule di Ippocrate:
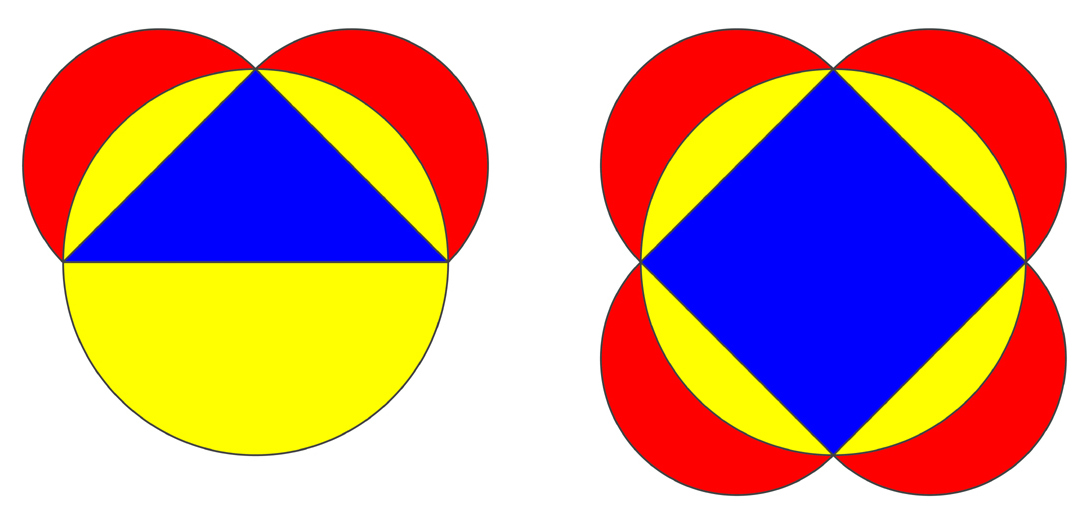
In questo caso, l’area indicata in rosso ha la stessa estensione di quella indicata in blu.
«Se poi il triangolo è isoscele, una lunula è uguale a mezzo triangolo. Questo è il primo caso storicamente accertato (la dimostrazione è attribuita a Ippocrate di Chio) in cui si è dimostrato che una figura rettilinea (il triangolo) è uguale a una curvilinea (la lunula).» Questo ci porta al logo della Mathesis:
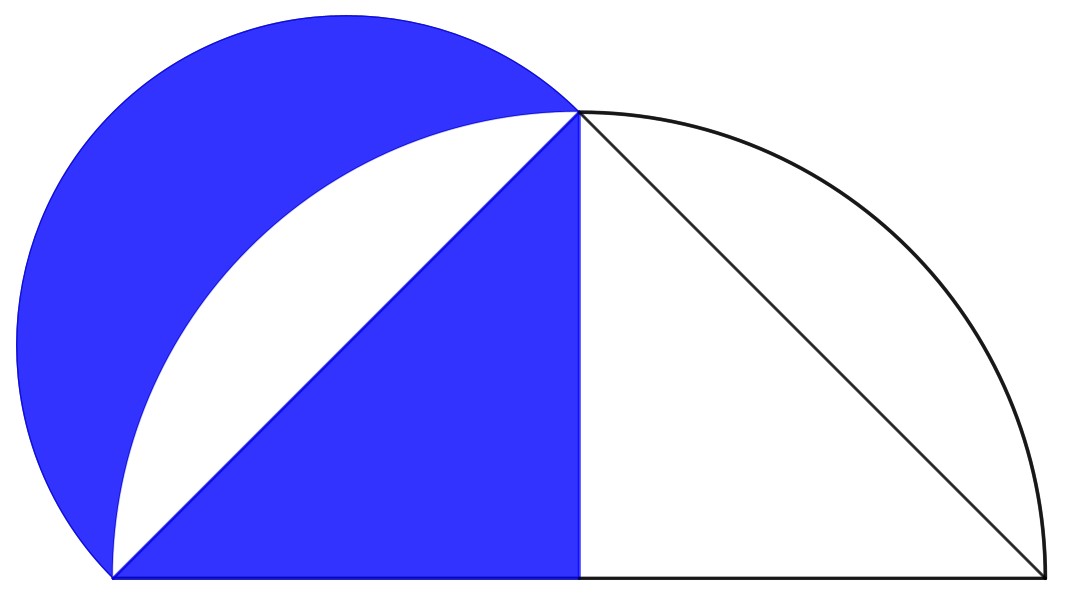
Una scelta non casuale, visto che la Mathesis è la «Società italiana di scienze matematiche e fisiche fondata nel 1895».
Il 14 marzo è, dal 2020, la Giornata internazionale della matematica e quest’anno il tema dei festeggiamenti è: Giocare con la matematica. Non potevano mancare un paio di giochi, in chiusura, presi dalle ultime due edizioni di Matematica senza Frontiere:
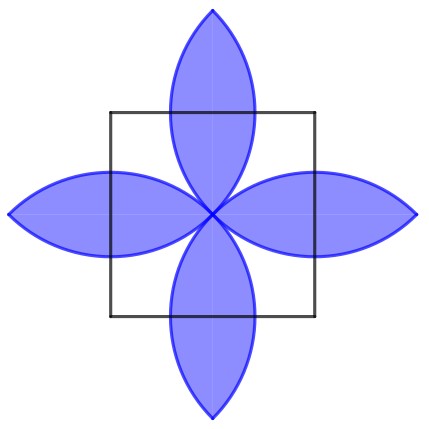

L’immagine a sinistra è stata proposta quest’anno: dopo averne indicato la costruzione, si chiedeva di determinare l’area della parte colorata, in funzione del lato del quadrato (indicato con a). continuando la tassellazione con altre circonferenze, è stato abbastanza semplice sottrarre, dall’area della circonferenza con raggio pari a metà diagonale del quadrato, un quadrato di lato a e moltiplicare il risultato per 2, ottenendo . Il disegno più colorato, invece, è stato proposto nella competizione dell’anno scorso e dovrebbe rappresentare la finestra con il vetro temperato di una chiesa. Sapendo che per il verde sono stati usati 400 cm2 di vetro, che superficie è necessaria per ricoprire il blu? (E scopriamo che si tratta ancora di 400 cm2).
Il cerchio è davvero una figura eccezionale e Munari dichiara nell’introduzione del suo libretto: «Il cerchio è una figura essenzialmente instabile, dinamica: dal cerchio nascono tutti i ruotismi, tutte le inutili ricerche del moto perpetuo». E dal cerchio è giunto a noi p, come dimenticarlo?
Buon pi-day a tutti!
PS: In allegato i file Geogebra per realizzare le immagini
Circonferenza febbraio 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: circonferenza
Durata: 120 minuti
Circonferenza gennaio 2024
Verifica di matematica, classe terza liceo scientifico.
Argomento: circonferenza
Durata: 110 minuti
Circonferenza e poligoni gennaio 2021
Verifica di geometria, classe seconda liceo scientifico.
Argomento: circonferenza, poligoni inscritti e circoscritti.
Durata: 60 minuti.
Circonferenza ottobre 2020
Verifica di geometria, classe seconda liceo scientifico.
Argomento: geometria euclidea, circonferenza.
Durata: un'ora.
Circonferenza febbraio 2020
Verifica di matematica, classe terza liceo scientifico.
Argomento: circonferenza e disequazioni irrazionali.
Durata: due ore.
Geometria euclidea maggio 2019
Verifica di matematica, classe seconda liceo scientifico.
Argomento: geometria euclidea.
Durata: un'ora.
Debito matematica terza settembre 2017
Verifica di matematica, classe terza liceo scientifico.
Verifica di recupero di settembre.
Durata: due ore.
BergamoScienza 17

© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy
