Visualizza articoli per tag: matematica
Profilo dei partecipanti
FONTI
In base al modo in cui i partecipanti hanno avuto accesso al questionario, possiamo distinguere tre categorie:
- 3AS: i partecipanti sono stati contattati personalmente dagli alunni della classe o dall’insegnante, tramite WhatsApp
- Social: i partecipanti hanno avuto accesso al link condiviso sui social (Instagram e Facebook)
- Contatti di contatti: chi ha ricevuto il questionario dagli alunni della classe ha poi contribuito a diffondere ulteriormente il questionario, inviandolo ai propri contatti
La maggior parte delle risposte (313) ci è pervenuta tramite nostri contatti diretti; le restanti risposte si suddividono quasi equamente tra social (172) e conoscenti dei nostri contatti (189).
È necessario, quindi, fare un paio di premesse:
- La nostra inesperienza nel porre le domande, combinata con l’accesso al questionario tramite i social, ha generato alcuni malintesi e alcune risposte sono, quindi, assenti o vaghe
- «Per essere attendibile, un campione deve essere rappresentativo della popolazione, ossia deve riprodurre su scala ridotta gli stessi dati rilevati per l’intera popolazione»[1]. È evidente che il nostro campione non può essere considerato rappresentativo della popolazione, visto come sono state raccolte le risposte. Evidenzieremo meglio la cosa proseguendo e confrontando i nostri dati con quelli rilevati dall’ISTAT.
GENERE ED ETÀ
Analizzando le risposte (674 in totale), abbiamo cercato di ricostruire il profilo di coloro che hanno partecipato al sondaggio, focalizzandoci sul genere, l’età e il grado di istruzione. Il 59% dei partecipanti era costituito da donne e le età sono indicate nel grafico seguente e suddivise in base al genere:
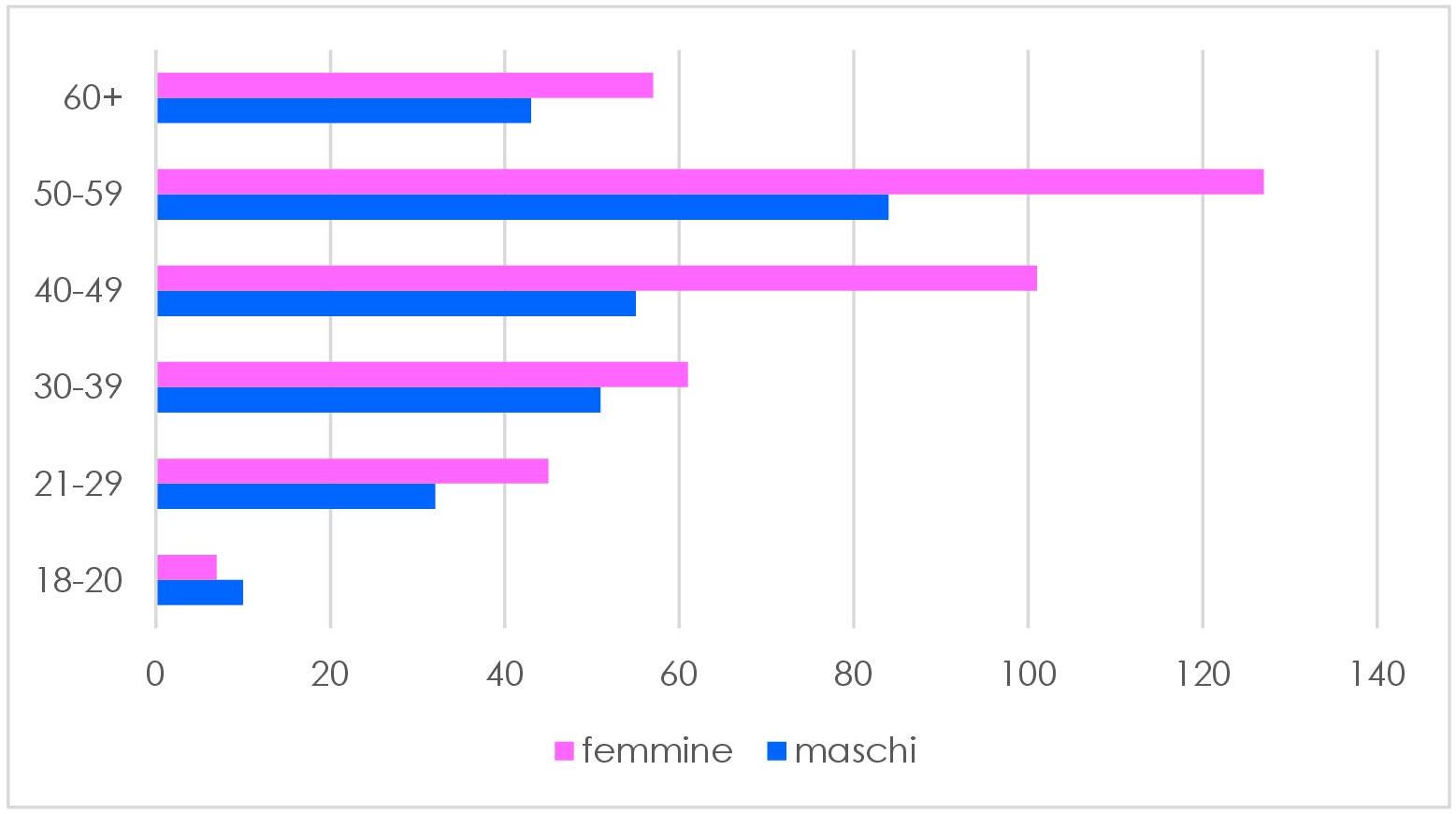
È importante riconoscere che la fascia di età 18-20 è la meno significativa, visto che hanno partecipato solo 18 persone (meno del 3%). Inoltre, visto che, per la maggior parte, i partecipanti sono ancora impegnati nella formazione, abbiamo deciso di non inserire i loro dati nei grafici successivi. La fascia più nutrita è quella dell’età compresa tra i 50 e i 59 anni (31%), nella quale è presente ancora una maggioranza femminile (127 risposte contro 84). La seconda fascia più numerosa è quella 40-49 (23%), mentre le altre tre fasce, oltre ad essere equamente distribuite per genere, hanno raccolto più o meno lo stesso numero di risposte.
Per verificare quanto il campione fosse poco rappresentativo della popolazione italiana, almeno in termini di età, abbiamo confrontato i dati dei nostri intervistati con quelli riferiti alla popolazione residente al 1° gennaio in Italia[2].
Soffermandoci anche solo sulla percentuale dei maschi e delle femmine,
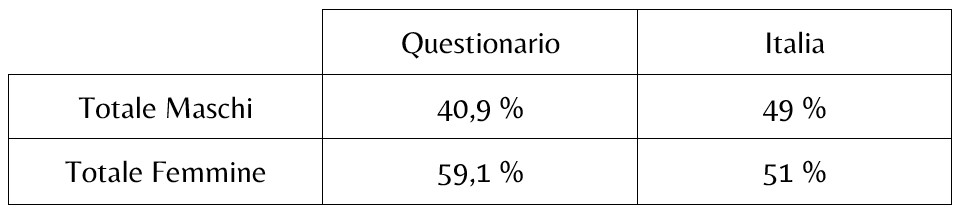
possiamo notare come la suddivisione per genere del nostro questionario non rispetti la suddivisione della popolazione italiana, dai 18 agli 85 anni.
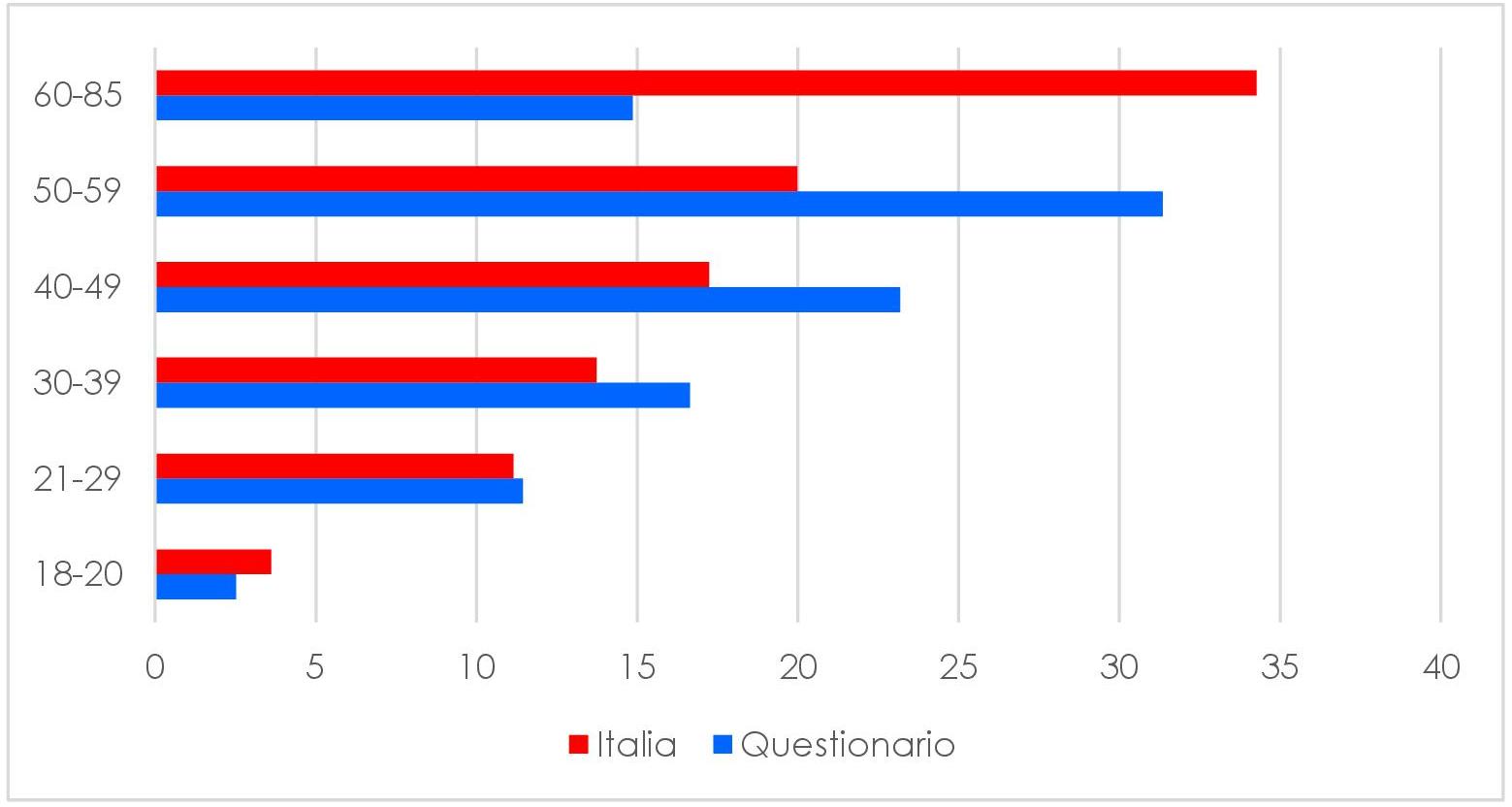
Se allarghiamo lo sguardo e consideriamo la suddivisione per età, vediamo parecchie incongruenze, ma prima è necessario precisare che la fascia di età più alta non era stata da noi definita, indicandola semplicemente come “60 e più”. Ripensando al campione intervistato, al fatto cioè che l’età più alta è quella dei nostri nonni e che oltre una certa età è più raro che accedano ai social (e quindi al questionario), abbiamo considerato come tetto gli 85 anni.
Già solo la suddivisione per età, quindi, ci restituisce il profilo di un campione che non può essere considerato rappresentativo della popolazione italiana.
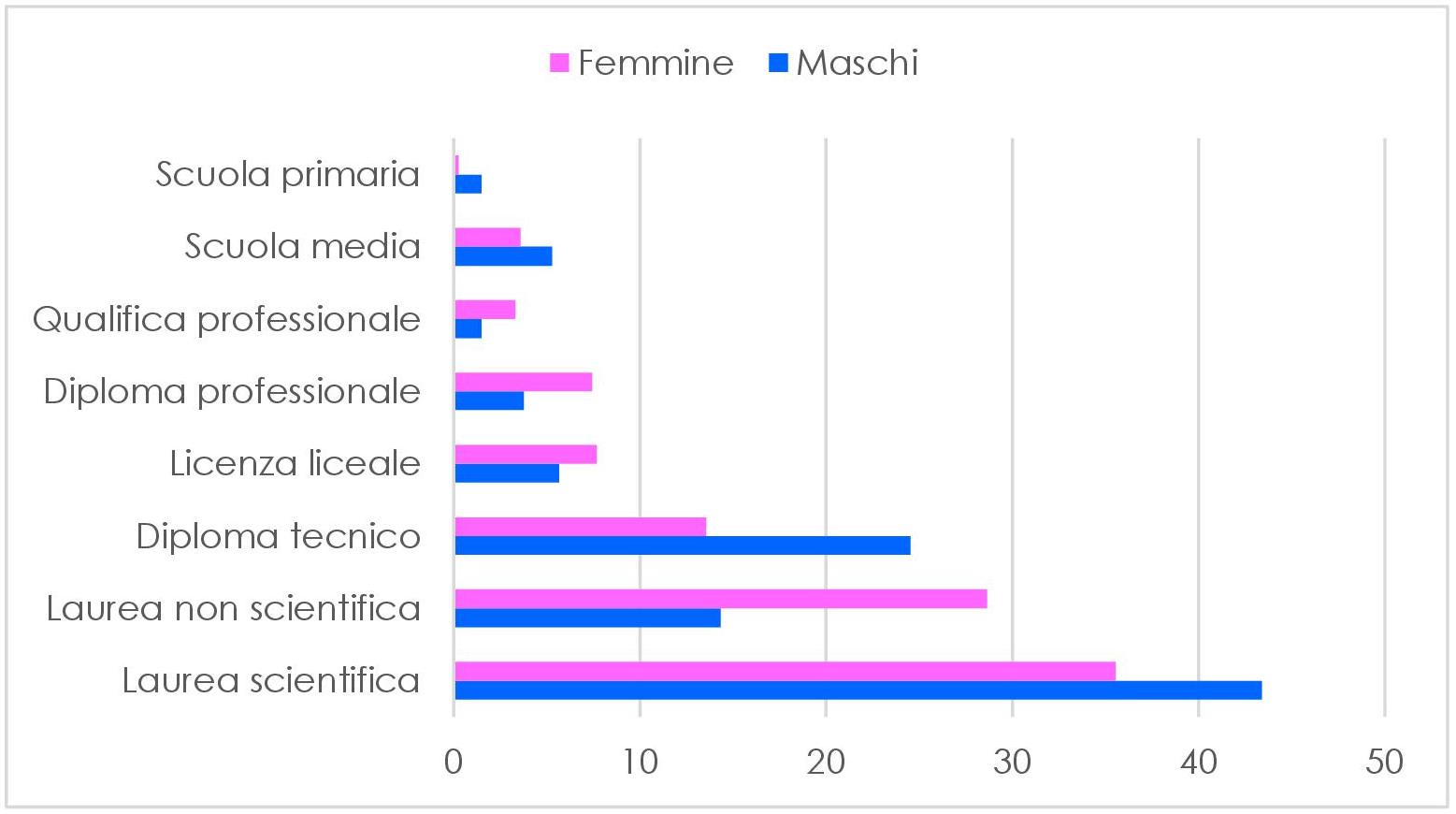
TITOLO DI STUDIO:
Dai grafici suddivisi per titolo di studio, possiamo notare una netta superiorità dei laureati, seguiti dai diplomati in materie tecniche. Possiamo notare che il numero delle licenze liceali è inferiore al numero dei diplomi tecnici, ma questo può essere dovuto al fatto che, mediamente, chi sceglie di frequentare un liceo prosegue con gli studi universitari, mentre è più probabile che un diplomato all’istituto tecnico chiuda il proprio percorso di studi dopo il diploma. Pochi sono i votanti che hanno interrotto il proprio percorso scolastico prima della scuola secondaria di secondo grado e, in genere, hanno superato i 60 anni di età, ma questo può essere dovuto al diverso obbligo scolastico: sebbene dal 1948 fosse stato imposto un ciclo di istruzione della durata di minimo otto anni, spesso la maggior parte dei bambini finiva solo la scuola primaria, nonostante le medie fossero obbligatorie. Si iniziò a frequentare obbligatoriamente la scuola media solo dal 1963, cioè per la fascia d’età che oggi è al di sotto dei 70 anni. Man mano che ci si avvicina alle fasce d’età più giovani, il grado di istruzione si innalza, grazie all’obbligo scolastico portato a 16 anni nel 2006[3]. È aumentato, inoltre, il numero di laureati, a seguito del decreto del 1999 con il quale vennero riformati i corsi di studio universitari, creando la laurea triennale e quella specialistica, e alcune professioni hanno visto un cambio di titolo di studio, basti pensare alla formazione infermieristica che, fino al 1995, è avvenuta nelle scuole regionali ed è diventato successivamente universitaria.
Quanto detto non vede differenze sostanziali nei generi, anche se i diplomi risultano essere distribuiti in maniera più omogenea tra le donne, e per gli uomini si tratta soprattutto di diplomi tecnici.
Infine, per ogni titolo di studio, abbiamo calcolato la percentuale di distribuzione in base al genere e abbiamo rilevato che:
- La scuola primaria, la scuola media, il diploma tecnico e le lauree scientifiche vedono una maggioranza maschile
- I restanti livelli di istruzione vedono una maggioranza femminile
Sembra quasi che l’ambito scientifico e tecnico siano un dominio maschile, stando al nostro campione!
[1] Bergamini, Barozzi, Trifone, Algebra.blu 1 con Statistica, Zanichelli, ISBN 9788808998828, capitolo a Introduzione alla statistica, p.a3
[2] http://dati.istat.it/Index.aspx?QueryId=42869#
[3] https://it.wikipedia.org/wiki/Storia_dell%27istruzione_in_Italia#La_scuola_nell'Italia_repubblicana
Prosegui con Matematica e mondo del lavoro
Un'indagine statistica
Mi capita spesso di domandarmi quanto la matematica sia presente in ambito professionale, quanto i miei (ormai ex) alunni debbano “fare i conti” con questa disciplina, tanto che al termine del percorso liceale, chiedo loro di tornare a trovarmi e di raccontarmi cosa hanno scelto di fare e quanto sia stato utile ciò che abbiamo studiato insieme. A volte sembra che il problema si esaurisca nell’utilità, ma non è così: da parte mia, c’è la necessità di capire se ho fornito loro abbastanza strumenti per affrontare il percorso professionale che hanno scelto, qualsiasi esso sia.
Confrontandomi con un medico, a settembre, mi sono sentita dire: «Diciamoci la verità: la matematica che uso nel mio lavoro è quella delle elementari: faccio le addizioni, qualche sottrazione, ma niente di veramente impegnativo!»
È stata questa la molla che ha fatto nascere in me l’esigenza di guardare più in profondità: davvero la matematica che usiamo tutti i giorni nel mondo professionale è solo quella dei primi anni delle elementari? Saltando da un pensiero all’altro, ha preso piede l’idea di realizzare un’indagine statistica e ne è nato un lavoro di educazione civica per la mia terza del liceo scientifico. Abbiamo proceduto per fasi, un po’ a tentoni: guardandomi indietro, mi rendo conto che avrei dovuto guidarli meglio, ma credo che il lavoro fatto abbia permesso loro di capire cosa significhi realizzare un’indagine statistica e, al tempo stesso, abbia fornito un’idea del mondo del lavoro un po’ più articolata. Quello che segue è l’articolo che, suddivisi a gruppi, i ragazzi hanno realizzato al termine del percorso, analizzando i risultati emersi dai questionari raccolti. Dopo aver definito gli obiettivi e i destinatari dell’indagine, gli alunni hanno partecipato attivamente alla stesura delle domande, alla scelta della modalità di somministrazione e alla correzione delle bozze; una volta approntato il modulo Google, hanno diffuso il questionario fra i propri conoscenti e, alla chiusura della consegna, hanno lavorato in gruppo, suddividendosi le domande da analizzare, realizzando una parte dell’articolo riportato di seguito e una parte del Power Point usato per presentare gli esiti dell’indagine alla classe.
In allegato:
- la presentazione che abbiamo realizzato in Power Point perché ogni gruppo potesse presentare al resto della classe il proprio lavoro
- il testo del questionario
2. Matematica e mondo del lavoro
3. Il rapporto con la matematica
Lavoro realizzato dalla classe 3AS del Liceo Scientifico "Decio Celeri" di Lovere (Bg)
Berlinghieri Tommaso, Bonomelli Anna, Cancellerini Claudia, Cocchetti Chiara, Colosio Sofia, Elmetti Davide, Gatti Gabriele, Mazzucchelli Filippo, Meloni Claudia, Oprandi Roberta, Romele Marta, Pe Sara, Previtali Ambra, Stefini Anastasia, Stofler Riccardo, Taboni Diego, Tomaini Filippo
5 febbraio 2024
Verifica di matematica, classe seconda liceo scientifico, recupero per assenti
Argomento: operazioni con i radicali e algebra con coefficienti irrazionali
Durata: 110 minuti
31 gennaio 2024
Verifica di matematica, classe seconda liceo scientifico.
Argomento: operazioni con i radicali e algebra con coefficienti irrazionali
Durata: 110 minuti
25 gennaio 2024
Verifica di matematica, classe terza liceo scientifico.
Argomento: circonferenza
Durata: 110 minuti
20 dicembre 2023
Verifica di matematica, classe seconda liceo scientifico.
Argomento: operazioni con i radicali
Durata: 120 minuti
14 dicembre 2023
Verifica di matematica, classe terza liceo scientifico.
Argomento: equazione di una parabola date alcune condizioni, tangenti a una parabola, segmento parabolico, fasci di parabole
Durata: 110 minuti.
25 novembre 2023
Verifica di matematica, classe seconda liceo scientifico.
Argomento: generalità sui radicali, domini e segni.
Durata: 50 minuti.
22 novembre 2023
Verifica di matematica, classe terza liceo scientifico.
Argomento: parabola, definizione, coefficienti, funzioni.
Durata: 60 minuti.
18 novembre 2023
Verifica di matematica, classe terza liceo scientifico.
Argomento: parabola, definizione, coefficienti, funzioni.
Durata: 60 minuti.

