La matematica è donna
Il profilo Instagram StorieScientifiche, la cui mission è, come scritto nella descrizione, il racconto della vita e delle scoperte «di uomini e donne che hanno contribuito, con le loro idee e i loro sogni, a portare avanti il progresso scientifico», il 24 marzo ha realizzato un post dedicato a Gigliola Staffilani, matematica presso il Massachusetts Institute of Technology, dove ricopre il ruolo di full professor (ovvero professore ordinario) in matematica pura, prima italiana di sempre e seconda donna della storia a ricoprire questo ruolo. La frase di apertura del post cattura l’attenzione: «Ho imparato, dopo molti anni, che dai fallimenti talvolta nascono grandi progressi». La sua storia ha dell’incredibile: famiglia contadina, orfana di padre a soli dieci anni, Gigliola sarebbe stata indirizzata dalla madre verso un futuro da parrucchiera, a causa della situazione complicata dal punto di vista economico che la sua famiglia stava vivendo. È solo per la sua bravura in matematica, per l’insistenza del fratello e per il sostegno dei professori che riuscirà a realizzarsi e ad avere un futuro nell’ambito della matematica. Tra gli aspetti interessanti della sua biografia che StorieScientifiche sceglie di mettere in evidenza, c’è il ruolo dell’insegnante del liceo scientifico Mario Illuminati, che le assegnava problemi difficili per i compiti a casa: «Io ero in grado di risolverli e mi rendeva estremamente felice».
Per un ulteriore approfondimento, si possono leggere le due interviste realizzate da Roberto Natalini per MaddMaths! La prima nel dicembre del 2010, e la piccola nota di redazione in apertura racconta parecchio di lei: si tratta di una segnalazione che i curatori dell’intervista hanno voluto fare dopo aver trascritto la registrazione, non solo perché è stato impossibile rendere l’accento abruzzese di Gigliola, che ora ha «qualche intrusione americana», ma anche perché «come si trascrive una risata?» Durante questa intervista, Natalini presenta la figura di Gigliola Staffilani a tutto tondo, facendola parlare delle sue scelte di vita, sia per lo studio che per la matematica, del ruolo delle donne, visto che è impegnata nella Association for Women in Mathematics (e fa notare che la situazione americana è peggiore di quella italiana), e fa infine un confronto tra il mondo della matematica americano e quello italiano. La seconda intervista, realizzata a luglio 2018, è apparsa originariamente sulla Newsletter della European Mathematical Society. 

Matematica (da amare e) da insegnare
Alla domanda di Roberto Natalini: «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?», Gigliola Staffilani risponde: «metà e metà. Credo che l’intuizione arrivi quanto ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte». Altro aspetto interessante è che, dopo Illuminati, la Staffilani parla di un altro docente, il professor Sally, che le fece un assegno di 1500 $ per permetterle di restare in America: «Penso spesso a quel momento, una fortunata coincidenza, completamente casuale, che sarebbe potuta non succedere. Se così fosse stato la mia vita sarebbe stata completamente diversa!» Gigliola stessa è un’insegnante e dichiara che ha bisogno di sentirsi felice al lavoro, altrimenti sarebbe «una pessima ricercatrice, insegnante e mentore». Anche Federico Benuzzi parla di felicità per rispondere alla domanda di un ragazzo, al termine di un suo spettacolo: «Vorrei fare l’insegnante, me lo consiglia?» La risposta di Federico (e se avete avuto occasione di assistere a un suo spettacolo, potete confermarlo) è accurata e sottolinea come, per poter fare l’insegnante, siano necessari due amori: l’amore per la materia, che non è scontato, e l’amore per i ragazzi. L’amore per la disciplina è fondamentale, perché c’è bisogno di una passione per accendere la passione nei ragazzi e per poter trasmettere il sapere in maniera efficace (e non sempre è sufficiente, aggiungo io…), mentre l’amore per i ragazzi permette all’insegnante di riconoscere le loro potenzialità e di apprezzare quanto, a loro volta, i ragazzi insegnano. «Credo che siano questi gli ingredienti fondamentali per continuare a insegnare anni senza “colpo ferire”. Segreto per svegliarsi tutte le mattine alle 6.20 felice di andare al lavoro. Pietra filosofale per restare eternamente giovani!» 

Matematica da comunicare
Pietro Minto, con il libro La seconda prova. Imparare la matematica, ci parla del suo secondo tentativo di affrontare lo studio della matematica, materia nella quale non aveva eccelso al liceo scientifico, per poter rifare la prova d’esame di matematica della maturità del 2006. Se avete dubbi in merito all’acquisto, leggere questo estratto pubblicato sul Post potrebbe aiutarvi a decidere: le pagine sono dedicate all’indagine sulla necessità (e utilità) delle incognite nell’algebra. Pietro Minto si concede anche la libertà di utilizzare formule semplici, guidandoci attraverso la storia della matematica.
Parlando di comunicazione della matematica, non si può non citare il quindicesimo anniversario di MaddMaths! (Auguri!). L’evento è stato ricordato sui social, condividendo l’articolo postato per il decimo anniversario. In effetti, quanto scritto da Roberto Natalini in quell’occasione è ancora attuale, richiamando «il dovere e la responsabilità di comunicare con il resto del mondo», visto che «la maggior parte dei non addetti ai lavori semplicemente ignora la ricerca matematica e la collega a sgradevoli ricordi scolastici». Nell’articolo si ricordano gli atti fondativi del sito, Roberto Natalini fa un po’ anche di mea culpa, ricordando i suoi precedenti, quando (forse) pensava «che chi si dedicava ad attività di comunicazione della matematica non avesse niente di meglio da fare». Dagli scarsi accessi dei primi tempi, dalle difficoltà nate dal fatto di essere dei pionieri, il sito MaddMaths! ha fatto parecchia strada, fino a diventare un punto di riferimento per i contenuti matematici che compaiono sulla rete.

Dialogando con la matematica
Giovedì 4 aprile si è svolta la terza diretta di quest’anno del canale IlariaF Math: l’ospite, Roberta Fulci, è una matematica, autrice di libri, redattrice e conduttrice di Radio3 Scienza, il quotidiano scientifico di Rai Radio 3. Nel corso della diretta, si è parlato di come Roberta Fulci sia approdata alla conduzione di questo programma, ideato da Rossella Panarese, un po’ per caso: appassionata di matematica, tanto da intraprendere il corso di laurea dopo il liceo classico, ha sempre pensato che si sarebbe dedicata alla ricerca, ma il suo senso di inadeguatezza l’ha spinta a scegliere di frequentare un master di comunicazione della scienza, per poter restare nell’ambito della matematica. Casualmente è arrivata alla redazione di Radio3 Scienza: obiettivo del programma che si trova a condurre è parlare di scienza rendendola accessibile a tutti e intrecciandola con altri aspetti della cultura e dell’educazione civica. Invitata dal pubblico, Roberta Fulci descrive il clima di collaborazione che caratterizza la preparazione di ogni puntata, che viene modificata fino all’ultimo minuto. Sempre su invito del pubblico, Roberta Fulci ha parlato anche delle sue emozioni una volta approdata alla facoltà di matematica, ricordando «il passaggio dalla sensazione di essere brava a quella di essere una rapa», visto che avere alle spalle il liceo classico non può che complicare le cose all’inizio dello studio universitario della matematica. Tra le puntate realizzate, Roberta Fulci parla in particolare della puntata dedicata alla matematica del colore, che ha avuto come ospite Edoardo Provenzi: la puntata non è più reperibile online, ma il professore ha realizzato una serie di articoli per MaddMaths! Interessante è la motivazione fornita per citare questa puntata: “Ho imparato tantissimo!” Nel corso della diretta, Roberta Fulci ha parlato anche delle sue opere: comincia con Ragazze con i numeri e Ragazze per l’ambiente, scritti insieme a Vicky De Marchi, per la collana Donne nella scienza di Editoriale Scienza e racconta di come, avendo scelto di dedicare una collana alle donne della scienza, le due sorelle che gestiscono la casa editrice si siano sentite dare delle kamikaze. E poi racconta del libro Il male detto, che parla del dolore fisico in termini matematici, visto che è un tentativo di darne una definizione. Vi invito a seguire con attenzione la diretta, visto che i racconti (che potete trovare anche nel libro) invogliano davvero alla lettura e la simpatia di Roberta Fulci è coinvolgente. 

Festeggiando la matematica
Nei giorni scorsi, si è parlato ovunque di matematica, visto che il 20 marzo è stato assegnato il premio Abel. Come tanti altri, anche il premio Abel viene paragonato al premio Nobel, ma questo, effettivamente, è quello che si avvicina di più: pare sia nato proprio per dare ai matematici un premio equivalente al Nobel, viene assegnato ogni anno dal re di Norvegia e può contare su un premio equivalente a 700.000 euro. Quest’anno la scelta è caduta su Michel Talagrand per i suoi contributi innovativi nell’ambito della teoria della probabilità e dell’analisi funzionale. Dopo la prima presentazione realizzata da Stefano Pisani, MaddMaths! ha dedicato ampio spazio al premio, con un articolo di Adriano Barra, che racconta i risultati e i riferimenti, enfatizzati sui social, al premio Nobel di Parisi. Più di tutto, a me è piaciuta l’ultima puntata di Ci vuole una scienza, il podcast del Post curato da Beatrice Mautino ed Emanuele Menietti, perché non solo ne hanno parlato in modo entusiasta, ma hanno raccontato molto bene e con semplicità i risultati ottenuti. Sessantottenne, Michel Talagrand si è confrontato fin da piccolo con il dolore, dato che a causa di problemi di vista ha dovuto passare un lungo periodo in ospedale: studente mediocre prima della malattia, aiutato dal padre a superare le ore di buio ed isolamento a suon di matematica, ha imparato il potere dell’astrazione. A distanza di tanti anni, dice: «il segreto del successo in matematica è di lavorare ogni giorno fino a essere esausti ma non di più». Dichiara di lavorare in questo modo a causa delle sue difficoltà (!) in matematica, legate a un “cervello lento” e a una “memoria terribile”: lavorando molto e cercando di capire anche le cose più semplici, è riuscito a superare le proprie difficoltà e a vincere numerosi premi. Con tono di meraviglia, Menietti racconta del sito internet del matematico, che, per quanto semplice e vecchia maniera, risulta interessante e ricco di spunti. Personalmente, sono rimasta molto colpita dal rimpianto legato ad una sua scelta compiuta come insegnante, che ricorda ancora con amarezza dopo più di quarant’anni. 

In chiusura, mi permetto un piccolo consiglio di lettura: lo spettacolo teatrale Il Signor Le Blanc di Maria Rosa Menzio pubblicato per Scienza Express. Continua il mio viaggio di approfondimento, mentre è ormai pronto lo script per il video con il quale parteciperò a #peopleformath2024! 

Buona matematica e buon cammino! Ci sentiamo tra TRE settimane!

Daniela

Traduzione dell’immagine allegata: “Perché dovrebbero bannare il libro di Miss Sweet dalla biblioteca della scuola?” “Non ci posso credere… non posso proprio crederci!” “Forse ci sono alcune cose nel suo libro che non capiamo…” “In quel caso, dovrebbero bannare anche il mio libro di matematica!”

«Il Signor Le Blanc» è stato pubblicato da Scienza Express nel settembre del 2020: si tratta della trascrizione di uno spettacolo teatrale, che è stato rappresentato in prima assoluta a novembre del 2018. L’autrice è Maria Rosa Menzio, ex matematica, nota per la formulazione e dimostrazione del teorema di Menzio-Tulczjew in geometria simplettica, che ha fondato l’associazione culturale “Teatro e Scienza”, essendo diventata nel frattempo drammaturga e saggista. Maria Rosa Menzio dirige il Festival “Teatro e Scienza” che ha luogo in autunno a Torino dal 2007 (con la sola esclusione dell’edizione del 2012), e che nell’edizione del 2018 ha avuto come tema Matematica e altri demoni. Il testo dello spettacolo è preceduto dalla trascrizione di un intervento del professor Franco Pastrone, del Dipartimento di Matematica dell’Università di Torino, pubblicato in Conferenze e Seminari dell’Associazione Subalpina Mathesis. Nel suo intervento, Franco Pastrone formula giudizi abbastanza pesanti nei confronti di Sophie Germain, la matematica alla quale quest’opera è ispirata, parlando di «episodi rimasti famosi, forse un po’ forzati al fine di esaltare la determinazione della ragazza», e, pur riconoscendo che all’epoca una donna con un interesse intellettuale era vista come una «curiosità da salotto […] ma non su un piano di parità», la descrive come una persona dal «carattere non facile, spigoloso, con un fondo di presunzione che concorse a guastarle i rapporti con illustri matematici». Forse la scelta di certe sottolineature è il riflesso di un periodo meno dotato di sensibilità in merito al gender gap, visto che la conferenza risale al 1994-1995.

Il sottotitolo dell’opera teatrale è «Matematica e Resistenza nella Francia occupata dai Nazisti» e infatti Maria Rosa Menzio pensa proprio ad un connubio tra matematica e resistenza. I protagonisti della rappresentazione teatrale sono un narratore, testimone di quanto succede in Francia durante la Seconda guerra mondiale e testimone del dramma dei lager, una protagonista femminile, Marianne, che rappresenta la Francia occupata dai nazisti e, inizialmente indifferente a quanto sta succedendo, poi diventa un’eroina partigiana, il professor Levi, docente di matematica ebreo imprigionato dai nazisti e amante di Marianne, e Von Guderian, ufficiale nazista crudele, che seduce Marianne con l’inganno. La vicenda si svolge tra il 1943 e il 1944 e fin da subito scopriamo che il professor Levi e Von Guderian si conoscono da tempo: il nazista non ha mai perdonato al professore la bocciatura in matematica. Durante la prigionia il professore comincia a raccontare a Marianne, secondo quella che sembra essere una prassi consolidata, la vicenda di Sophie Germain, che assume l’identità del Signor Le Blanc per poter studiare matematica e che sarà una delle poche a riconoscere il genio di Evariste Galois. Sophie Germain è riuscita a crearsi un posto in un mondo prettamente maschile, anche se per molto tempo non le è stata riconosciuta la sua grandezza, come dimostrato dall’assenza del suo nome sulla Tour Eiffel, nonostante sia stata una pioniera nello studio dell’elasticità dei metalli.

Il racconto è piacevole, originale e coinvolgente: per quanto vedere lo spettacolo sarebbe stato meglio, la lettura permette di immaginare la rappresentazione teatrale. Le metafore aiutano lo spettatore / lettore a cogliere tutta la negatività del nazismo e la necessità dell’eroismo, per poter far trionfare la giustizia.
Nella quarta di copertina leggiamo: «Amore, tradimento e redenzione, fino allo scontro tra due carri armati e alla morte di Marianne (travestita da ufficiale nazista proprio col nome di Le Blanc) in un finale commovente e inaspettato».

Verifica di matematica, classe terza liceo scientifico
Argomento: geometria analitica, ellisse e iperbole

Durata: 120 minuti

Verifica di matematica, classe seconda liceo scientifico
Argomento: equazioni di secondo grado

Durata: 60 minuti

Verifica di matematica, classe terza liceo scientifico
Argomento: geometria analitica, ellisse e iperbole

Durata: 120 minuti

Verifica di fisica, classe seconda liceo scientifico
Argomento: cinematica nel piano

Durata: 60 minuti

Pi greco!
Ho rimandato l’uscita di questa newsletter fino ad oggi, per poterla inviare proprio in occasione del Pi-Day! Perciò, al centro della scena non può che esserci la Giornata Internazionale della Matematica, che si festeggia dal 2019, proclamata dall’UNESCO e curata da un progetto dell’Unione Matematica Internazionale. Il tema di quest’anno è Playing with Maths – Giocare con la matematica ed è particolarmente interessante la Sfida Creativa proposta, «atta a vedere la matematica nel nostro ordinario, a riconoscere schemi in quello che vediamo tutti i giorni e immortalarli in un’istantanea»: hanno partecipato numerose scuole e alcune delle fotografie ispirano davvero matematica e spingono a realizzare qualcosa di unico. Il poster di quest’anno è bello e colorato, con sei indovinelli e giochi da risolvere. Sul sito di MaddMaths! è possibile vedere l’elenco degli eventi italiani.
MaddMaths! propone anche la terza edizione del CALENPLARIO: Riccardo Moschetti e Roberto Zanasi propongono una serie di problemi, riveduti da Maria Angela Chimetto e Sergio Zoccante, ogni tre giorni, (il martedì, il giovedì e il sabato) alle 3:14, dal 14 marzo fino al 28 giugno. Sarà possibile iscriversi e partecipare insieme ad altre persone. 

Pi greco in video
Non posso non condividere alcuni filmati realizzati da Mathematical Visual Proofs, il canale che si occupa di dimostrare per immagini alcuni risultati matematici. Il primo video è molto efficace nel mostrare l’area del cerchio usando il metodo di esaustione, e sfogliando il cerchio come se fosse fatto da una serie di strati che appaiono quasi impalpabili. Il secondo video è un’approssimazione molto grezza di pi greco: considerando una griglia quadrata di 101 punti con coordinate intere, colorando in blu i punti con coordinate prime tra loro e facendo il rapporto tra il numero dei punti blu e il totale dei punti, si ottiene sei volte il reciproco del quadrato di pi greco, grazie al quale si ottiene l’approssimazione di 3,12. Questa approssimazione mi ha ricordato, in qualche modo, quella proposta al Senato dello stato dell’Indiana, il 12 febbraio del 1897. Stando a Christopher Waldo, della Purdue University, quando nel 1916 l’Accademia delle Scienze dell’Indiana ha deciso di celebrare il proprio secolo di vita realizzando un volume con il quale sarebbero stati ripercorsi i maggiori risultati scientifici, Waldo ha citato un «singolo atto di prevenzione [che] rende maggior merito all’Accademia delle scienze dell’Indiana […] di qualsiasi contributo che abbia mai pubblicato o che possa mai pubblicare in futuro sui propri resoconti». Il risultato è quello di aver impedito che passasse una legge assurda, come gli stava raccontando un senatore, certo che fosse imminente un evento storico importante: «“Se passa questo emendamento – gli dice testualmente – stabiliremo per legge un nuovo e finalmente corretto valore di p. Pensi, professore: l’autore offre al nostro Stato gratuitamente l’utilizzo di questa scoperta nei nostri testi scolastici, mentre tutti gli altri Stati dovranno pagarci i diritti.”» Sul numero 61 di Prisma, in edicola da pochi giorni, è possibile leggere l’intero articolo di Marco Malvaldi: offre l’occasione per un’interessante riflessione sui bias cognitivi e sollecita la nostra attenzione sul rischio di fare affermazioni certe «su problemi dei quali abbiamo una comprensione troppo limitata anche solo per capire come sono sorti».
Magari se non vi piace 3,12 come approssimazione e non apprezzate nemmeno la proposta dello stato dell’Indiana, potete sempre scegliere di considerarlo uguale a 2: si parte da un semicerchio di raggio 1 e, quindi, di lunghezza pi/2, poi si costruiscono altri due semicerchi con raggio pari alla metà del precedente, ma in cui la somma delle semicirconferenze dà sempre lunghezza pi/2 e così via, fino a mostrare che le semicirconferenze si confondono con il diametro. Un po’ come nel caso della radice quadrata di 2 che diventa uguale a 2, confondendosi con l’ipotenusa. Eppure, se ingrandiamo l’immagine o se la guardiamo con gli occhi della matematica, scopriamo che la realtà non è come appare. Il quarto video confronta e^pi e pi^e, usando un ramo di iperbole e un piccolo integrale, mentre il quinto, comparso oggi, offre cinque diverse formule di pi in pi/2 minuti e usando solamente il disegno di un rettangolo di dimensioni 2 e 3, con quattro triangoli al suo interno. 

Pi greco e il carnevale della matematica
Il carnevale della matematica di marzo è uscito proprio questa mattina, alle 3.14: ospitato sul blog Dropsea, quindi da Gianluigi Filippelli, amministratore e divulgatore per il sito Edu INAF e per l’Osservatorio Astronomico di Brera, ha per tema, ovviamente, il pi greco. Presentato attraverso un video, nel quale ci vengono raccontate le caratteristiche del numero 176, è davvero ricco di contenuti, spunti, curiosità. L’articolo con il quale ho partecipato è intitolato Cerchi fra i banchi e di fatto è un percorso, fatto per immagini e ricco di file Geogebra, tra le indicazioni ministeriali della seconda liceo scientifico. Ho cominciato con la rappresentazione a colori di 180 cifre del pi greco, e ho proseguito con alcune costruzioni geometriche realizzate con Geogebra, dalla circonferenza per tre punti non allineati, alla costruzione delle tangenti da un punto esterno, ai punti notevoli di un triangolo, fino ad arrivare al cerchio dei 9 punti, che mi ha ricordato un’opera di Lanfranco Bombelli citata nel libretto Il cerchio di Bruno Munari. La conclusione ha per protagoniste le lunule di Ippocrate, il logo della Mathesis e un paio di giochi proposti nella competizione Matematica senza frontiere. 

Playing with Maths
Seguendo il tema della Giornata Internazionale, IlariaF Math ha deciso di riprendere le dirette sul suo canale, aprendo la rassegna il 7 marzo scorso con Paolo Alessandrini, autore del libro Matematica in campo. Dopo la domanda di rito su cosa sia per Paolo la matematica, e vi spoilero subito che non poteva che definirla un gioco (anche se non aggiungo altri dettagli), Paolo ha parlato di bellezza e di efficacia. Poi, seguendo il tema del libro, Paolo ha raccontato come il gioco del calcio porti con sé, oltre all’ovvia fluidodinamica, al moto parabolico e alla geometria del fuorigioco, anche la topologia, i poliedri (visto che il pallone è un poliedro!), il calcolo combinatorio e tanto altro. Come sempre, Ilaria è un’ottima padrona di casa e Paolo ha sempre un sacco di curiosità con cui intrattenere il pubblico: se vi siete persi la diretta, dovete assolutamente guardarlo! Stasera, alle 20.45, avrà luogo la seconda diretta, durante la quale Ilaria intervisterà Daniele Aurelio, fisico, insegnante, componente del gruppo Physics4Teenagers e coordinatore del Mathsjam di Pavia, l’unico attivo in tutta Italia.
Un paio di settimane fa, Davide Calza e Riccardo Moschetti hanno pubblicato un nuovo video per il Math-Segnale: si tratta dell’analisi matematica del problema numero 15 del World Math Championship del 2022. Il gioco è davvero interessante e la capacità di Davide e Riccardo di tirarne fuori un problema di carattere generale e di riuscire a dimostrarlo in modo semplice non manca mai di meravigliarmi. La descrizione del video è sufficiente a farci incuriosire: «La sfida tra Alice e Bob sembra quasi impossibile. Senza avere praticamente nessuna informazione, e bendata, Alice dovrà trovare il modo di girare tutte le pedine della scacchiera in modo che abbiano lo stesso colore, tutto questo mentre Bob può modificare in continuazione il tavolo da gioco. Come farà?» L’algoritmo descritto mi ha ricordato, in qualche modo, la sequenza di mosse per risolvere il cubo di Rubik e, visto che mia figlia dodicenne è un’appassionata, ho deciso di farle vedere il filmato: come risultato, si è presentata con una benda, una griglia quadrata 2x2 e quattro dischi colorati, chiedendomi di fare Bob. Conoscendo il gioco, ho cercato di renderle le cose difficili, scegliendo la configurazione migliore, ma il risultato è stato che è riuscita a vincere in 7 mosse! 

Consigli di lettura
Dall’ultima newsletter ho realizzato tre recensioni: la prima riguarda due libri per ragazzi, A Pisa con Galileo e A Cambridge con Newton, scritti da Silvia Merialdo, con le illustrazioni di Gaia Aloisio ed Emanuela Carbonara. La protagonista è Andrea che con Galileo Galilei va alla scoperta dell’universo e con Newton della gravità, passeggiando con loro nei luoghi dove hanno vissuto. I due scienziati vengono descritti a tutto tondo, tanto che non può che infastidire il carattere litigioso e un po’ burbero di Newton. Semplici, chiari e simpatici, i due racconti contribuiscono ad avvicinare alla scienza i giovani lettori, stimolandone la curiosità.
La seconda proposta è un testo di non facile reperimento, trattandosi di Ultima lezione a Gottinga di Davide Osenda. È un fumetto, pubblicato nel 2009, impreziosito dall’introduzione di Piergiorgio Odifreddi, anche grazie al fatto che le tavole sono state esposte in versione gigante sui muri dell’auditorium di Roma durante il Festival della Matematica. La seconda presentazione è di Andrea Plazzi, editor nel campo dei fumetti, noto per la sua consulenza per le opere di Leo Ortolani. Il fumetto è davvero piacevole, anche se l’argomento non è semplicissimo, visto che l’ultima lezione ruota attorno all’ipotesi del continuo di Cantor.
Il terzo libro è davvero per tutti: è Matematici di profilo, di Umberto Bottazzini. Si tratta di 48 brevi biografie, o, per meglio dire, ritratti, di matematici e matematiche attraverso i quali è possibile ricostruire la storia della matematica. I profili sono stati pubblicati su Il Sole 24 Ore con il quale Bottazzini ha collaborato a lungo, come dimostrato da questo articolo del 2020: L’affascinante storia di «pi greco». Questa affascinante storia si apre con il Don Giovanni di Mozart e il problema della quadratura del cerchio, ovvero il «problema di costruire con riga e compasso un quadrato di area uguale a quella di un cerchio dato». Passando attraverso la Bibbia e re Salomone, Bottazzini cita Il pendolo di Foucault di Umberto Eco e La montagna incantata di Thomas Mann, ma poi ricorda i grandi personaggi che hanno reso immortale questo numero (o forse è questo numero ad aver reso immortali i matematici che l’hanno studiato!). Così ci viene ricordato che il celebre simbolo è stato scelto da Eulero, mentre la dimostrazione dell’irrazionalità risale al 1768 ad opera di Johann Heinrich Lambert. Che dire poi della trascendenza? Ferdinand von Lindemann dà la soluzione definitiva al rompicapo della quadratura del cerchio nel 1882: con riga e compasso è impossibile! 

Sono aperte le iscrizioni al secondo convegno nazionale CARME: Ricerca in pratica: la ricerca in didattica della matematica per la scuola. Si terrà a Pistoia, il 17 e 18 maggio prossimi, e le iscrizioni si chiuderanno il 15 aprile. 

Buona matematica e buon cammino! Ci sentiamo tra TRE settimane!

Daniela 

Fonte dell’immagine: https://shorturl.at/ioQ39

Si può dire che p sia il protagonista del programma di seconda liceo scientifico: nella prima parte dell’anno scolastico, ci si immerge nell’insieme dei numeri reali e gli irrazionali sono posti al centro della scena. Come dimenticare l’irrazionale per eccellenza?

Nell’immagine è riportata una rappresentazione visiva di alcune cifre decimali di p, 180 per la precisione, che è facile ricostruire assegnando al colore la cifra corrispondente. L’immagine è stata realizzata per uno dei cartelloni esposti durante la seconda partecipazione al Festival di BergamoScienza dell’istituto dove insegno, che ha avuto come protagonista il cerchio.

La classe seconda è il momento in cui si alza il livello di difficoltà: dopo aver risolto equazioni, disequazioni e sistemi lineari, si affrontano, con gli irrazionali nella cassetta degli attrezzi, i problemi di secondo grado ed ecco che in geometria fa la sua comparsa la circonferenza, definita come il luogo geometrico dei punti del piano equidistanti da un punto fisso, il centro.

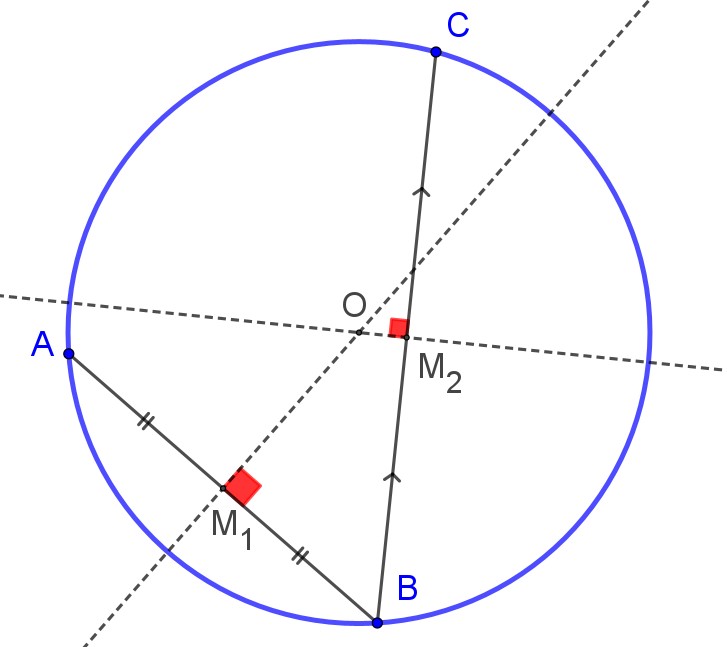
Uno dei primi teoremi che si incontrano riguarda la circonferenza passante per tre punti non allineati, e la dimostrazione permette, in realtà, di fare una semplice costruzione con Geogebra, evitando di usare lo strumento “Circonferenza – tre punti”. Il teorema fa intravedere i teoremi sulle corde, che presto permetteranno di vederne la lunghezza in relazione alla loro distanza dal centro, e di realizzare che davvero l’asse di una corda passa per il centro.

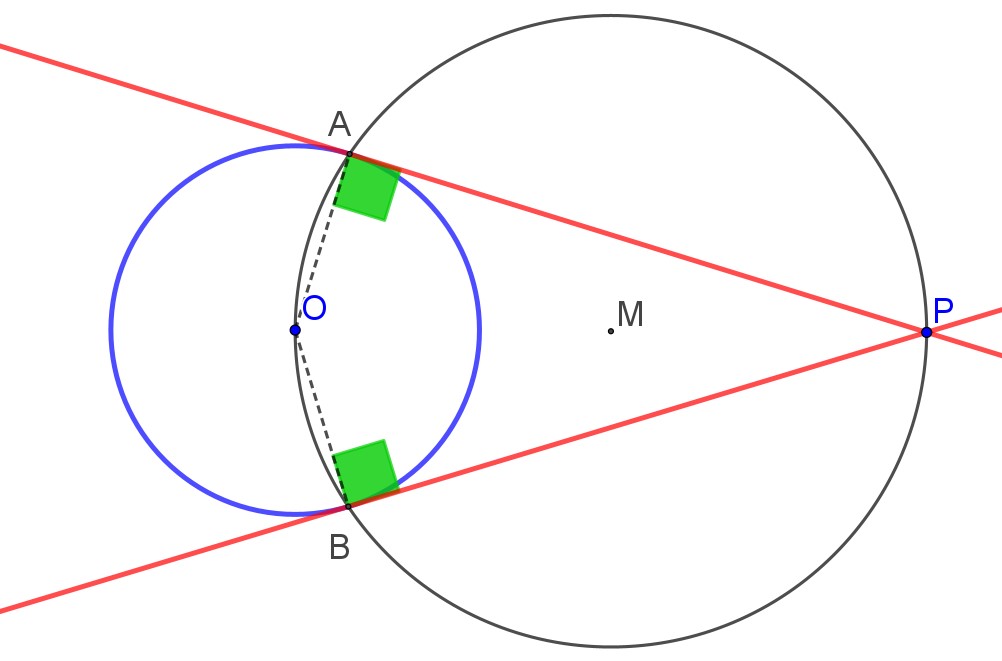
Il passo successivo è quello di considerare le circonferenze in relazione alle rette e, in particolare, in relazione alle tangenti. Così, può capitare di dover imparare a costruire le rette tangenti a una circonferenza tracciate da un punto esterno, basandosi sul fato che una retta tangente a una circonferenza è perpendicolare al raggio passante per il punto di tangenza. Questo risultato ci regala un anticipo sui triangoli rettangoli inscritti in una semicirconferenza.

Il percorso in matematica assomiglia a una danza, con un passo avanti e uno indietro, a creare una coreografia, ritornando su cose già viste, ma affrontandole in maniera diversa, e così nel capitolo successivo le circonferenze incontrano i triangoli, sempre inscrivibili in e circoscrivibili a una circonferenza, ma non solo:

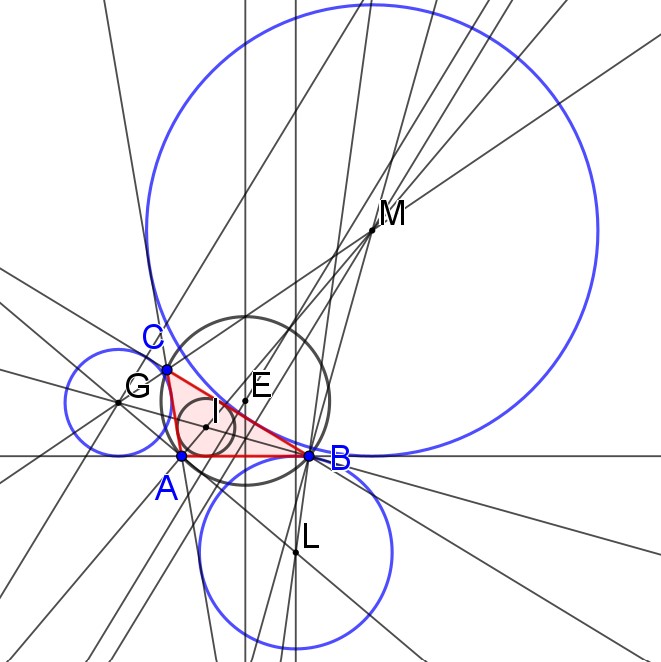
Tra il circocentro (E) come punto di incontro degli assi e centro della circonferenza circoscritta, l’incentro (I) punto di incontro delle bisettrici e centro della circonferenza inscritta, il triangolo ABC incontra anche altre tre circonferenze, di centri rispettivamente M, L e G, detti excentri, punti di incontro della bisettrice dell’angolo interno non adiacente con le bisettrici degli altri due angoli esterni e quelle blu sono le circonferenze exinscritte, tangenti a un lato e al prolungamento degli altri due. È stato vedendo un’opera di Lanfranco Bombelli (1921/2008), pittore, incisore e architetto, che ho pensato a questa rappresentazione e…

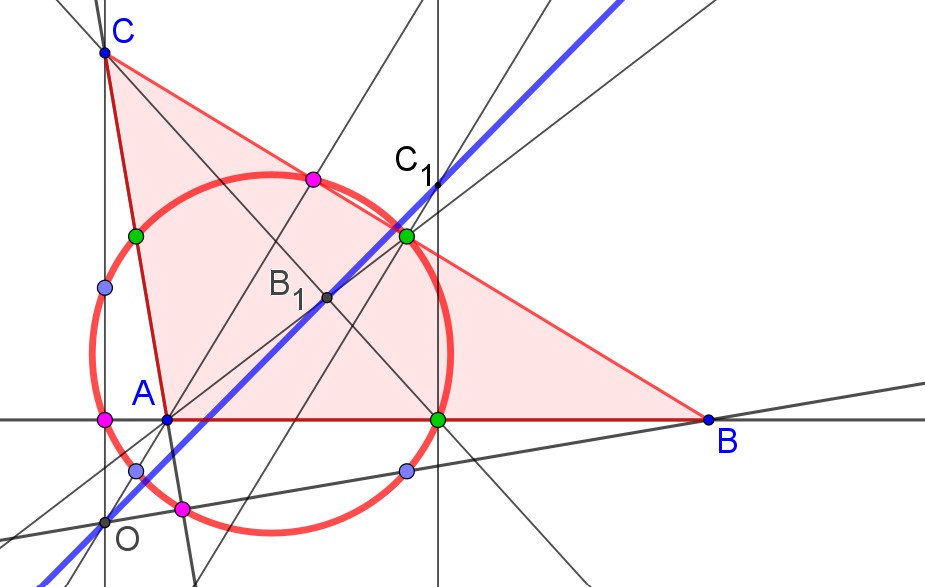
Ripensare al Cerchio per nove punti è stato un attimo: eccola in tutta la sua bellezza! Indicata in rosso passa per tre terne di punti: quelli rappresentati in verde sono i punti medi dei lati del triangolo; quelli in fuxia sono i piedi delle altezze relative ai lati e poi ci sono gli ultimi, più difficili da definire, perché, individuato con O l’ortocentro (il punto di incontro delle altezze di un triangolo), essi sono i punti medi del segmento che ha per estremi O e un vertice del triangolo. Ho scoperto, giusto oggi, che questa circonferenza è nominata come Cerchio di Feuerbach (almeno, stando a quanto dichiarato su Wikipedia), matematico tedesco, fratello del più famoso filosofo. Qualcuno, invece, la nomina come cerchio di Eulero, ma credo che, in questo caso, il celebre matematico potrebbe accontentarsi della paternità della retta, che passa per tre punti notevoli: ortocentro, baricentro, circocentro.

Mentre scorro le pagine del libretto di Bruno Munari intitolato Il cerchio (e scopro ora che ci sono anche Il quadrato e Il triangolo…) dove ho trovato il riferimento a Lanfranco Bombelli, mi imbatto nelle voci “Raggio decrescente” e “Raggio crescente”:

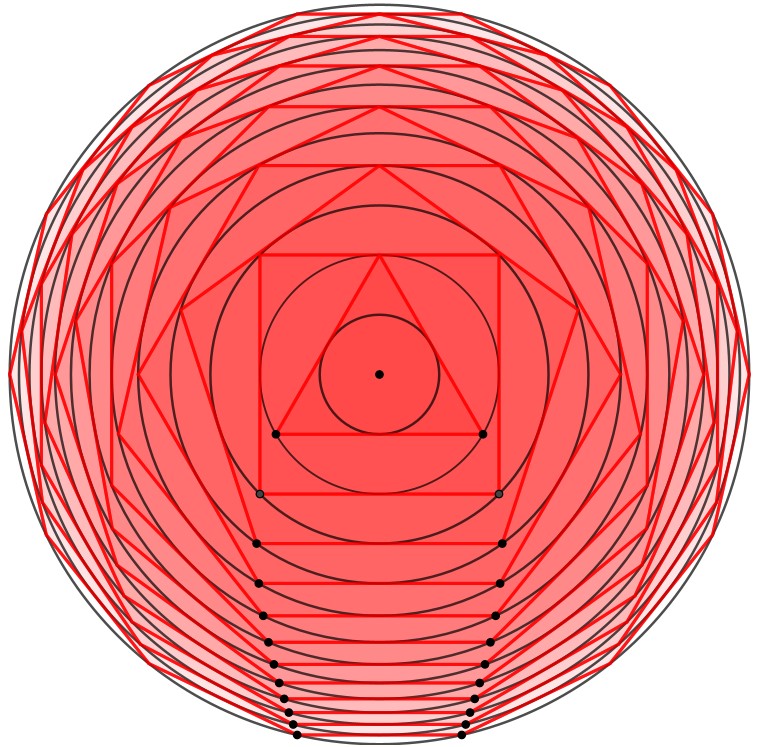
Mi è parso così interessante, che non ho resistito alla tentazione di realizzare quello crescente con Geogebra, arrivando fino al poligono di 14 lati (inventandomi metodi ingegnosi per rappresentare quelli da 7, 9, 11 e 13 lati). Mi piace citare, in particolare, ciò che scrive Munari, oltre alle indicazioni per la costruzione: «Può sembrare che il raggio, aumentando oltre ogni limite, diventi infinito; invece si avvicina a un limite che è circa dodici volte quello del raggio del cerchio primitivo», esattamente come quello decrescente «si avvicina a un limite che è circa un dodicesimo di quello del raggio del cerchio primitivo».

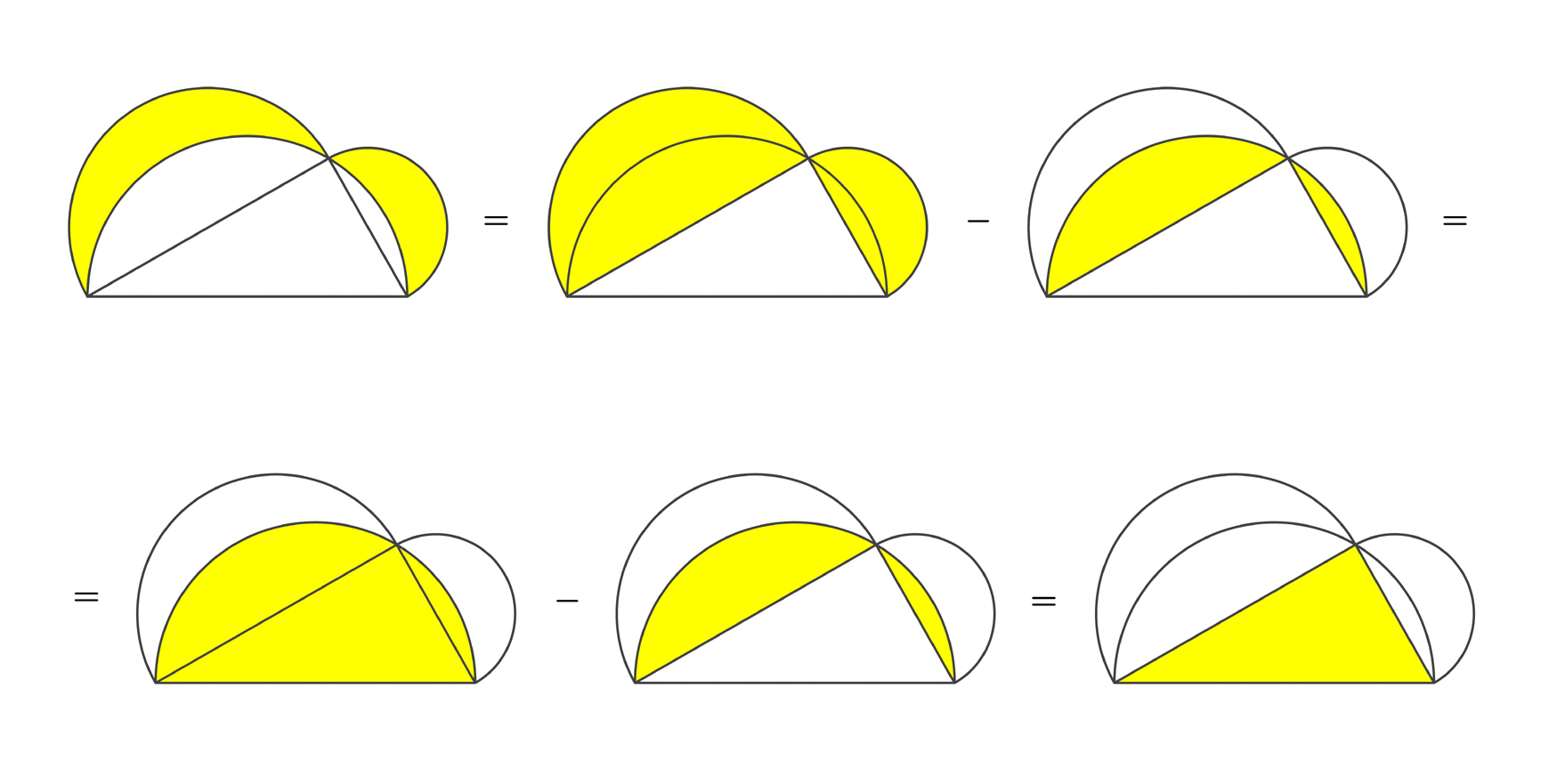
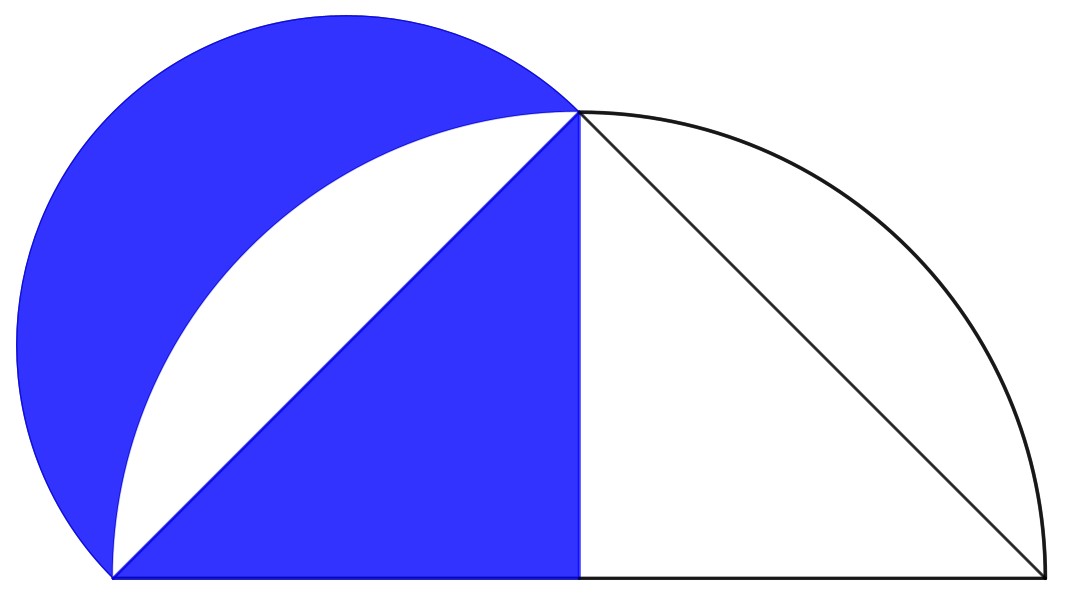
Non ho resistito alla tentazione di riprendere in mano anche questa simpatica dimostrazione senza parole, che utilizza le lunule e il triangolo di Pitagora. Il triangolo rappresentato è rettangolo e ha come lato di appoggio l’ipotenusa. Sui due cateti vengono costruite (e colorate) le lunule, la «parte di piano compresa fra due archi circolari di raggio diverso aventi in comune gli estremi e giacenti dalla stessa parte rispetto alla corda comune». In questo caso, il raggio delle semicirconferenze esterne è pari a metà del cateto e il centro è il punto medio del cateto, mentre l’arco più interno è la semicirconferenza con raggio pari a metà dell’ipotenusa e centro nel punto medio della stessa. La prima differenza è facile, la seconda, invece, ha a che fare con il teorema di Pitagora: come riportato sul sito del Giardino di Archimede, il museo della matematica: «Nell’enunciato del teorema di Pitagora, i quadrati possono essere sostituiti da altre figure, come ad esempio triangoli, esagoni, o anche figure irregolari, purché simili tra loro». Chi ha avuto modo di visitare il museo, avrà provato a mettersi alla prova con i diversi puzzle realizzati proprio con questo teorema di Pitagora generalizzato.

Sul sito, troviamo poi il caso particolare delle lunule di Ippocrate:

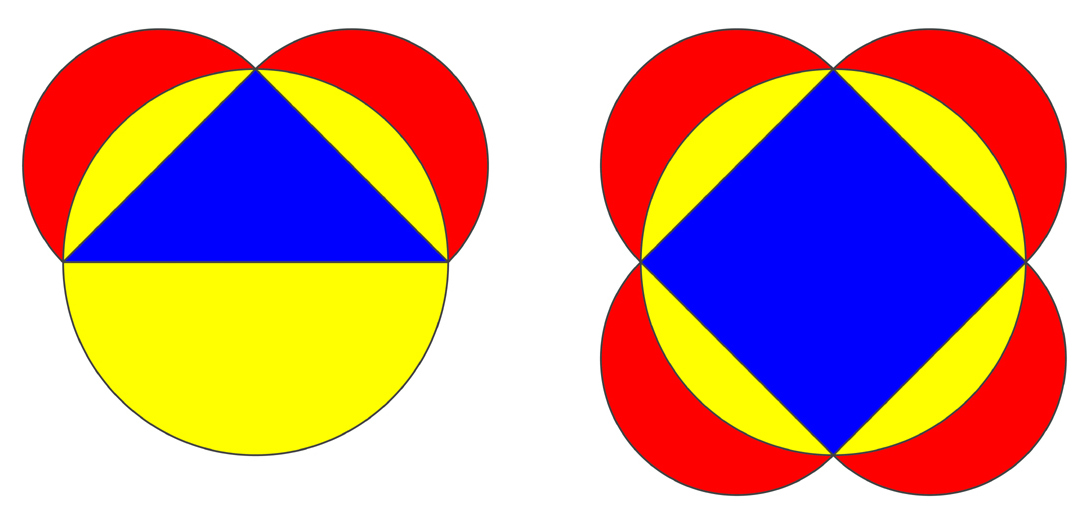
In questo caso, l’area indicata in rosso ha la stessa estensione di quella indicata in blu.

«Se poi il triangolo è isoscele, una lunula è uguale a mezzo triangolo. Questo è il primo caso storicamente accertato (la dimostrazione è attribuita a Ippocrate di Chio) in cui si è dimostrato che una figura rettilinea (il triangolo) è uguale a una curvilinea (la lunula).» Questo ci porta al logo della Mathesis:

Una scelta non casuale, visto che la Mathesis è la «Società italiana di scienze matematiche e fisiche fondata nel 1895».

Il 14 marzo è, dal 2020, la Giornata internazionale della matematica e quest’anno il tema dei festeggiamenti è: Giocare con la matematica. Non potevano mancare un paio di giochi, in chiusura, presi dalle ultime due edizioni di Matematica senza Frontiere:

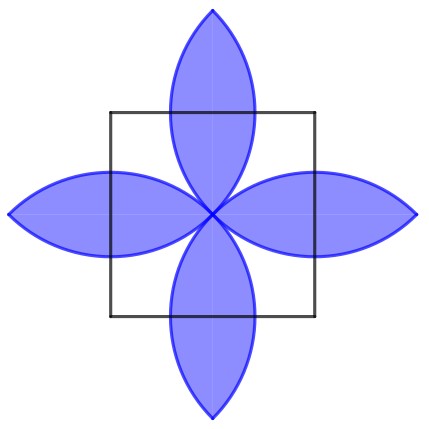
L’immagine a sinistra è stata proposta quest’anno: dopo averne indicato la costruzione, si chiedeva di determinare l’area della parte colorata, in funzione del lato del quadrato (indicato con a). continuando la tassellazione con altre circonferenze, è stato abbastanza semplice sottrarre, dall’area della circonferenza con raggio pari a metà diagonale del quadrato, un quadrato di lato a e moltiplicare il risultato per 2, ottenendo . Il disegno più colorato, invece, è stato proposto nella competizione dell’anno scorso e dovrebbe rappresentare la finestra con il vetro temperato di una chiesa. Sapendo che per il verde sono stati usati 400 cm² di vetro, che superficie è necessaria per ricoprire il blu? (E scopriamo che si tratta ancora di 400 cm²).

Il cerchio è davvero una figura eccezionale e Munari dichiara nell’introduzione del suo libretto: «Il cerchio è una figura essenzialmente instabile, dinamica: dal cerchio nascono tutti i ruotismi, tutte le inutili ricerche del moto perpetuo». E dal cerchio è giunto a noi p, come dimenticarlo?

Buon pi-day a tutti!

PS: In allegato i file Geogebra per realizzare le immagini

«Matematici di profilo» è stato pubblicato nel novembre del 2021 dalla Casa Editrice Sole24 ore e l’autore è Umberto Bottazzini, uno dei maggiori esperti internazionali nell’ambito della storia e dei fondamenti della matematica. Nel 2006 ha vinto il Premio Pitagora per la divulgazione matematica e nel 2015 l'Albert Leon Whiteman Prize, il riconoscimento per la storia della matematica bandito dall’American Mathematical Society, «per le sue numerose opere in Storia della Matematica, in particolare sulla nascita della Matematica moderna in Italia e sullo sviluppo dell'Analisi nel XIX e inizio XX secolo».

Le 48 brevi biografie di questo libro «provengono da articoli apparsi nel corso degli anni nelle pagine de Il Sole 24 Ore-Domenica»: riorganizzate in ordine cronologico, rielaborate e liberate dai «riferimenti occasionali alle circostanze che hanno motivato gli articoli originali», costituiscono una storia della matematica discreta, ovvero fatta da una successione di punti distinti (i matematici), uniti da incontri e circostanze. Come nel gioco dei puntini della Settimana Enigmistica, il lettore riesce a individuare il disegno finale solo procedendo nella lettura, e il quadro restituisce ai suoi occhi una storia della matematica in versione semplificata, ma ricca di dettagli. «Questo libro non si rivolge agli specialisti», dichiara Bottazzini in apertura e ha come obiettivo il superamento dell’«idea che i matematici siano esseri bizzarri e stravaganti». Tra le pagine ritroviamo «uomini e donne che vivono immersi nelle temperie del loro tempo, protagonisti nel corso dei secoli della grande avventura della matematica», che hanno dimostrato «di possedere straordinarie capacità di invenzione, immaginazione e fantasia». I profili contengono notizie biografiche scevre di dettagli, visto che, ad esempio, gli anni di nascita e di morte sono riportati in un elenco alla fine del libro: si tratta, soprattutto di biografie matematiche, che mostrano come la vita dei protagonisti sia intessuta di matematica e, al tempo stesso, come la storia della matematica sia ricca di vita. Ogni profilo inizia con un evento importante, quello che ha spinto l’autore a scegliere il matematico per questa rassegna, in cui spesso, il protagonista è un altro matematico, che, con la sua autorevolezza, mostra l’importanza del lavoro svolto. Come in un ritratto pittorico, Bottazzini, con sapienti pennellate di parole, condensa in poche righe il lavoro svolto, la sua importanza nel percorso storico, mentre i legami con i precedenti e i successivi ci permettono di cogliere come nessun matematico sia un’isola, e quanto quegli incontri siano stati determinanti per costruire il nuovo percorso. Ogni capitolo è dedicato a un matematico o a una matematica, solo occasionalmente a una coppia di matematici, che non possono essere separati perché troppo presenti l’uno nella vita dell’altro.

La rassegna non poteva che aprirsi con Pitagora e la dimostrazione matematica, Euclide, autore di «uno dei testi più influenti nell’intera storia dell’umanità», e Archimede, che ha legato il proprio nome alle basi della matematica. Con un salto di quattordici secoli, si arriva a Fibonacci, che porta in Europa la sapienza orientale, a Piero della Francesca, con il suo Trattato d’Abaco, a Luca Pacioli con la Summa, fino a Cardano, «una delle figure più straordinarie e controverse del Rinascimento», il cui nome non può essere separato da quello di Tartaglia. Galileo non poteva che essere tra i protagonisti, con il suo lavoro sull’infinito, le «“meraviglie”», le «“fantasticherie” e [i] paradossi», mentre Torricelli e Cavalieri arrivano nella parte finale del suo percorso. Cartesio apre la strada a una nuova matematica, mentre Fermat, «genio universale» e «matematico dilettante», con Pascal contribuisce alla nascita della probabilità. Leibniz e Newton condividono «la gloria dell’invenzione del calcolo infinitesimale», mentre i Bernoulli, oltre ai grandi contributi matematici, partecipano alla nascita di «uno dei più grandi matematici della storia», il prolifico Eulero. Maria Gaetana Agnesi ha lasciato un segno nella storia della matematica con le sue «Istituzioni analitiche ad uso della gioventù italiana» e con la sua versiera, mentre Girolamo Saccheri, nel voler liberare Euclide dai suoi nei, contribuirà alla nascita delle geometrie non euclidee. Lagrange, “nuovo Newton” per i contemporanei, è «uno dei più grandi matematici di sempre», mentre Laplace contribuisce a dare visibilità al teorema di Bayes; l’insegnamento di Cauchy «“era una nube oscura, illuminata talvolta da lampi di genio”», come scrive il contemporaneo Menabrea. Sophie Germain, seconda donna della rassegna, condivide il capitolo con Maryam Mirzakhani: entrambe eccezionali e vittime di una morte prematura, ma la vicenda della Germain, con la necessità di fingersi uomo per poter studiare matematica, non può che ricordare un romanzo. Abel e Galois sono accomunati dalla gioventù e dalla loro capacità di lasciare un segno indelebile nella matematica, contribuendo alla nascita di una nuova branca, l’uno con le funzioni ellittiche, l’altro con i gruppi. Gauss, Bolyai e Lobačevskij sono uniti dal quinto postulato di Euclide e dalla nascita delle geometrie non euclidee, mentre Riemann non poteva mancare nella rassegna, essendo stato «un grande matematico, senza dubbio il più profondo e geniale dell’epoca e tra i più grandi della storia». Dedekind, è stato una «sorgente inesauribile di idee e una fonte continua di ispirazione», Cantor ha legato il proprio nome all’infinito, e Boole «ha segnato la nascita della moderna logica matematica». Visto il periodo, Bottazzini dedica un intermezzo ai matematici del Risorgimento, citando in particolare Luigi Cremona, Enrico Betti e Francesco Brioschi, e procede poi con Sofya Kovalevski, che sentiva che il suo destino era «“servire la verità, cioè la scienza, e tracciare la strada per le donne perché ciò significa servire la giustizia”». Poincaré abbraccia con la sua opera «non solo la matematica ma i più diversi campi della fisica», tanto da essere stato candidato tre volte al Nobel, mentre Ricci Curbastro e Levi-Civita, forse meno noti, ci hanno regalato, secondo Einstein, «“un meraviglioso esempio di come la matematica ha fornito lo strumento teorico per una teoria della fisica”». La rassegna italiana procede con Volterra, «un gigante, che ha dominato il panorama della matematica e della scienza non solo italiana nei primi trent’anni del secolo scorso», Enriques, «uno dei maestri della “scuola italiana” di geometria algebrica», e Castelnuovo, che «ha imposto i geometri italiani sulla scena matematica internazionale». Ramanujan non può che essere ricordato insieme a Hardy, mentre Hilbert porta con sé i celebri ventitré problemi che hanno contribuito a dare forma alla matematica successiva. Brouwer parla di matematica “intuizionista”, mentre le lezioni di Emmy Noether «divennero un punto di riferimento per i giovani matematici in Germania e all’estero». Gödel ha ottenuto «fondamentali risultati che hanno segnato lo sviluppo della moderna logica matematica», von Neumann ha contribuito all’«organizzazione funzionale alla quale si ispirano ancora oggi le macchine», e Wiener ha imparato da Hardy che «“la matematica era non solo una materia che si poteva studiare ma anche discutere e vivere”». Il secondo intermezzo è dedicato alla matematica tra le due guerre, con la lungimiranza della fondazione Rockefeller che darà luogo a «un programma di emergenza per far fronte alla emigrazione degli scienziati ebrei». Durante e dopo la guerra, troviamo Turing, pioniere dell’Intelligenza Artificiale, e de Finetti, con la concezione soggettivistica della probabilità; De Giorgi è ricordato per il suo appassionato impegno civile e per aver dimostrato il diciannovesimo problema di Hilbert, contemporaneamente a Nash, vincitore, con Nirenberg, del Premio Abel nel 2015. L’anno dopo il premio è andato a Wiles, colui che ha dimostrato l’ultimo teorema di Fermat, e che è uno dei due matematici ancora viventi di questa rassegna. L’altro è Perel’man, legato a Poincaré per merito della topologia, protagonista dell’incomprensibile rifiuto della medaglia Fields e del premio del Clay Institute.

Ogni matematico di questa rassegna apre la strada al successivo e, al tempo stesso, deve la propria grandezza a chi l’ha preceduto.
Il libro è poco impegnativo, ma ricco di spunti e curiosità interessanti, e offre l’opportunità di sentire la vera voce dei matematici, viste le numerose citazioni.

Verifica di fisica, classe terza liceo scientifico
Argomento: leggi dei gas ideali e teoria cinetica

Durata: 60 minuti