
Mostra (5)
Euclide Megarense philosopho, solo introduttore delle scientie mathematice. Diligentemente rassettato, et alla integrità ridotto, per il degno professore di tal scientie Nicolo Tartalea Brisciano
Il volume è una traduzione dal latino in volgare dell'opera "Elementi" di Euclide, suddivisa in quindici libri, nei quali sono presentati i principi e le nozioni della geometria noti al tempo del matematico greco. Inoltre Tartaglia si dedicò all'insegnamento della geometria euclidea siccome era parte fondamentale nei suoi studi della balistica.
Tartaglia spiega nello spazio dedicato al traduttore perché ha deciso di tradurre l'opera: per permettere agli studenti di usufruire degli studi di Euclide sull'aritmetica e la geometria.
Spiega inoltre la visione di Euclide riguardo a queste ultime due discipline, descritte, in particolar modo la geometria, secondo la visione filosofica di Aristotele e Platone: l'uomo è guidato dal desiderio di sapere che non è altro che intendere per dimostrazione. Per Platone la sapienza non è altro che una cognizione delle cose divine e umane e viene divisa in due parti distinte, cioè speculazione e operazione, ovvero teoria e pratica; mentre Aristotele nella Metafisica afferma che il fine della speculazione, ovvero della pratica speculativa, è la verità, la quale si trova proprio nella matematica e nella geometria che sono del "puro cibo della vita intellettuale". Il geometra è visto come uno che non si cura delle figure, delle forme, delle linee, del materiale, ma si cura soltanto delle figure così come sono, di come l'occhio sensibile vede le figure sensibili, perciò anche le figure viste nella mente sono tanto vere quanto quelle viste dall'occhio.




Opera in mostra: Euclide Megarense philosopho, solo introduttore delle scientie mathematice. Diligentemente rassettato, et alla integrità ridotto, per il degno professore di tal scientie Nicolo Tartalea Brisciano. Secondo le due tradottioni. Con vna ampla espositione dello istesso tradottore di nuono aggiunta...
In Venetia: appresso Curtio Troiano, 1565 (In Venetia : appresso Curtio Troiano, 1566).
Accademia Tadini, Lovere, Biblioteca storica, ATL H.VI.3
OPUSCOLI DI GEOMETRIA E BALISTICA di Leonardo Salimbeni
Il volume scelto è un volume sugli studi geometrici e balistici dell'onorevole ingegnere Leonardo Salimbeni. Il volume si apre con la dedica al signor Giovanni Battista da Riva e successivamente si trova l'introduzione al primo opuscolo dove si parla di geometria piana. Alla fine del capitolo, si trova un’appendice a quest’ultimo dove non si parla più solo di teoria ma anche di pratica: sono presenti infatti moltissime formule matematiche per spiegare la geometria. Vengono presentati anche dei problemi di esempio.
Nella seconda metà del volume si apre il secondo opuscolo, dedicato alla balistica, più in particolare sul getto delle bombe specialmente nei piani inclinati.
Nella prefazione del secondo opuscolo del proprio manoscritto, Salimbeni spiega di come ormai ai suoi tempi “tutte le nazioni di europa” fossero piene di artiglieri e di conseguenza di artiglieria e armi da fuoco. Dice anche di quanto sia fondamentale la matematica per permettere che queste armi venissero usate al meglio: importantissimo è il ruolo della geometria; afferma infatti di voler trovare un nuovo modo per “tirere le armi sopra ai pieni inclinati in un modo più sicuro di quelli usati in precedenza”.
Bisogna notare infatti che l’opuscolo nel quale parla di basilica presenta precedentemente due opuscoli sulla geometria che servono anche per introdurre l’argomento sull’artiglieria.
Il rapporto tra la geometria analitica e il moto dei proiettili infatti è strettamente collegato: per esempio, un corpo lanciato da un cannone partendo con una certa velocità iniziale ed un certo angolo percorre una traiettoria parabolica sotto l'azione della sola accelerazione di gravità. ma questo verrà scoperto successivamente a Galileo, quando si capirà che la traiettoria di un proiettile è per l’appunto un moto parabolico.
Come Salimbeni, anche Tartaglia dedicò parte della sua vita allo studio della balistica; dal 1534 infatti si diede all’insegnamento della geometria euclidea, disciplina strettamente collegata alla balistica. Così nel 1537 pubblica il primo volume che parla del moto dei corpi nello spazio: nel volume è presente un volumetto balistico nel quale cerca di fornire indicazioni utili a un migliore uso delle armi da artiglieria, prendendo le mosse da teorie di balistica basate sul principio dell’impetus (moto violento di cosa o persona che si spinge contro un oggetto con tutta la sua forza).
Lo studio riguardava la gittata massima dei proiettili delle bombarde. Tartaglia trovò che la gittata massima si aveva per un angolo di tiro di circa 45°, valore che coincide con i calcoli teorici per una traiettoria nel vuoto. E questo perché, utilizzando proiettili pesanti e piuttosto lenti, la resistenza dell’aria risultava trascurabile.
Curioso è però il fatto che inizialmente Tartaglia non volesse scrivere un trattato sulla balistica: riteneva infatti che fosse immorale costruire armi che andassero ad uccidere o comunque a ferire delle persone. Forse proprio perché lui stesso era stato ferito da un’arma in giovane età? Nonostante ciò però, quando l’invasione da parte dei Turchi era alle porte, Tartaglia decise di creare il volumetto balistico per migliorare la prestazione delle artiglierie ed evitare l’invasione turca.
Successivamente cercò di pubblicare anche delle tavole di tiro dove voleva classificare ogni arma specificando l’inclinazione e i dati principali per far si che l’arma lavorasse al massimo della potenza e per dare altre informazioni sui lanci e sul moto del proiettile in modo diretto. Purtroppo tartaglia era in anticipo di parecchi anni sullo studio dell'argomento e la sua idea non riscosse il giusto successo.

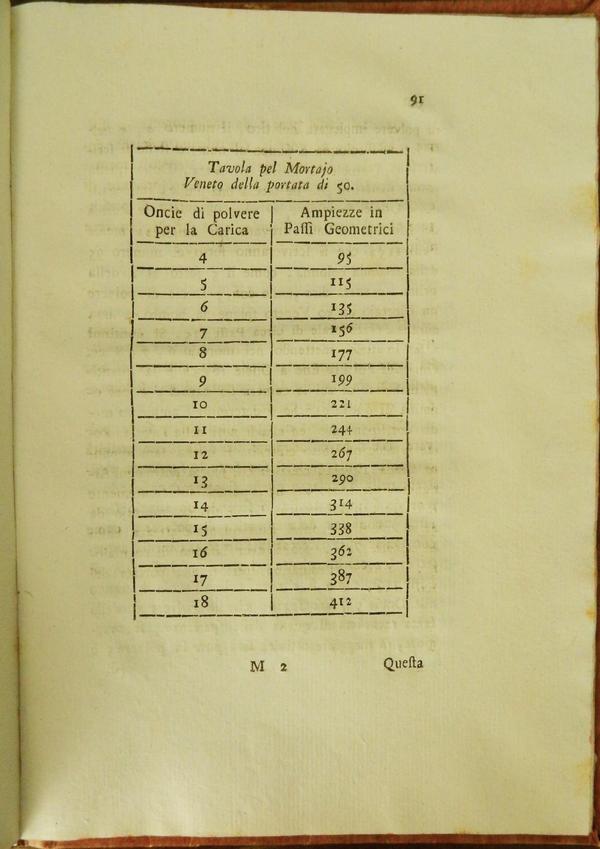
Opera in mostra: Opuscoli di geometria e balistica di Leonardo Salimbeni capitano d'ingegneri e professore di matematica nelle scuole militari di Verona.
In Verona: per gli eredi di Marco Moroni, 1780.
Accademia Tadini, Lovere, Biblioteca storica, ATL H.II.1
Inoltre, risponde alla domanda:
“Quale e quante siano le scientie, overo discipline Mathematice. Le scientie, overo discipline dette Mathematice, secondo il volgo sono molte, cioè Arithmetica, Geometria, Musica, Astronomia, Astrologia, Cosmographia, Geographia, Corographia, Perspettiva, Specularia, la Scientia de pesi, la Architettura e molte altre. Ma alcuni Sapienti, prendono solamente le quattro prime, cioè Arithmetica, Geometria, Musica e Astronomia: e tutte le altre dicono esser subalternate, cioè dependente dalle dette quattro: alcuni altri moderni (per alcune sue ragioni) vogliono che le dette Mathematice siano cinque, però che alle dette quattro aggiungono la Prospettiva.”
La descrizione può essere confrontata con l’Allegoria delle scienze matematiche pubblicata nel volume di Tartaglia (vetrina 2).
LA DISFIDA
Disfida Matematica (secondo l’enciclopedia Treccani): gara pubblica, in voga nel sec. 16°, nella quale un matematico sfidava un altro matematico a risolvere un dato problema, mediante un apposito cartello d’invito (cartello di matematica disfida).
Nel 1526 muore Scipione Dal Ferro, che aveva scoperto una formula risolutiva per le equazioni di terzo grado. La formula non era stata resa pubblica, ma era nota agli allievi di Dal Ferro. Tra essi, Antonio Maria del Fiore, detto Fior, che decise di appropriarsene.
Tartaglia, nel 1535, trovò una formula risolutiva per le equazioni di terzo grado che permetteva di risolvere più casi rispetto alla formula di Fior. Quest’ultimo sfidò Tartaglia in una disfida, che fu vinta da Nicolò Tartaglia.
Il matematico iniziò a guadagnare fama, ma scelse di mantenere segreta la formula, per poterla comunicare lui stesso in una propria opera. Tuttavia, un intellettuale del tempo, Gerolamo Cardano, lo convinse a rivelargli la formula risolutiva, con la promessa di mantenerla segreta. Cardano però rivelò la formula al suo miglior allievo, Ludovico Ferrari, che grazie ad essa trovò il procedimento per svolgere le equazioni di quarto grado.
Cardano voleva pubblicare la scoperta di Ferrari e Tartaglia, ma era vincolato dal patto con quest’ultimo. Tuttavia, Cardano venne a sapere che la formula risolutiva di Tartaglia era già stata scoperta da Scipione Dal Ferro, perciò pubblicarla non sarebbe stato un tradimento nei confronti dell’amico.
Nel 1545 venne così pubblicato l’Ars Magna di Cardano, testo che conteneva le formule risolutive relative alle equazioni di terzo e quarto grado, compresa la formula scoperta da Tartaglia.
Egli, infuriato e sentendosi tradito dall’amico, nel 1546 pubblicò un libro, Quesiti et inventioni diverse, in cui esponeva la propria versione di tutta la vicenda.
Cardano non replicò all’attacco subìto, lasciando che a farlo per lui fosse l’allievo Ferrari. Il 10 febbraio 1547, Ferrari lanciò a Tartaglia un pubblico cartello di disfida matematica, caratterizzato da toni sprezzanti e denigratori.
La resa dei conti arrivò il 10 agosto 1548, giorno in cui Tartaglia e Ferrari incrociarono le armi matematiche a Milano, nella chiesa di Santa Maria del Giardino.
Spinto dal supporto della sua “gran comettiva”, Ferrari appariva in grado di esporre le proprie argomentazioni con rapidità, sicurezza e piena padronanza di metodi e formule, dimostrando di possedere una preparazione matematica ben superiore alle attese di Tartaglia. Il quale, a suo dire innervosito e deconcentrato dal pubblico, non sembrava riuscire a tenere testa al rivale. E dopo solo un giorno di discussioni, abbandonò la contesa.
Due testi nella biblioteca del conte Tadini mostrano l’interesse per le scienze matematiche nel Settecento nelle università e nelle accademie militari.
Leonardo Salimbeni
Ricerche sull'equazioni di terzo grado
Verona: Dionigi Ramanzini, 1782
Accademia Tadini, Lovere, Biblioteca storica.
Leonardo Salimbeni approfondisce gli studi presso il Collegio Militare di Verona. In quella sede, ottiene ottimi risultati “per prontezza, acume e penetrazione nell’apprendere le scienze matematiche e le discipline militari”. I risultati dei suoi studi saranno esposti in numerose pubblicazioni.
Il volume esposto, un opuscolo di ricerche relative alle equazioni di terzo grado suddiviso in due capitoli; nella vetrina successiva (► vetrina 4) è presentato un trattato di balistica.
Giuseppe Cassella
Saggio d'un tentativo per risolvere l'equazioni di tutt'i gradi.
Napoli: Pietro Perger, 1788.
Accademia Tadini, Lovere, Biblioteca storica.
Giuseppe Cassella, astronomo e matematico, è stato professore di Matematica all’Università di Padova, poi di Astronomia nel Real Collegio della Marina e di Meccanica nel Real Collegio di Artiglieria e nella Regia Università degli Studi a Napoli.

LEONARDO SALIMBENI
Leonardo Salimbeni nacque a Spalato nel 1752, figlio di un militare veneziano di alto rango, Giovanni Salimbeni, e fratello maggiore di Sebastiano Salimbeni.
Nel 1764 si iscrisse al collegio militare di Verona.
Per affari militari viaggiò a Zante e a Zara, mentre per il suo talento scientifico, il direttore del collegio Antonio Moser de Filseck lo condusse in un viaggio in Dalmazia e Albania.
Nel 1794 divenne direttore del collegio come suo padre prima di lui.
Nel 1783 sposa Alfonsa Moronati, sorella di Libera, moglie del conte Luigi Tadini.
Nel 1791 ampliò la dogana del commercio di Verona e divenne un membro della Società Italiana, detta dei Quaranta, nello stesso periodo in cui ne fu un socio Alessandro Volta.
Conobbe Isabella Teotochi, nata Albizzi, nel 1778 e fece parte del suo salotto culturale al quale partecipavano personaggi del calibro di Foscolo, Byron e Canova. Viaggiò con Isabella a Roma dove ebbe l’opportunità di visitare lo studio di Canova e di conoscere Vincenzo Monti.
Il 27 maggio 1796 incontrò a Brescia Napoleone, che descrisse in una lettera-resoconto.
A Verona Bonaparte propose a Salimbeni di dirigere una scuola del genio militare e dell'artiglieria. Il comandante francese lo convinse a trasferirsi a Milano, sede della Repubblica Cisalpina.
Nominato direttore della scuola militare ebbe come allievi suo figlio Giovanni e Giovanni Foscolo, fratello del poeta.
Dopo la discesa delle truppe austro-russe in Italia nel 1800, i beni di Leonardo Salimbeni vennero confiscati.
Sebbene nel 1801 Salimbeni, insieme al figlio Giovanni, avesse parteggiato per il ritorno dei Francesi in Italia, rifiutò un incarico alla scuola militare di Francia e all'Università di Modena.
Dopo l’ordine di Napoleone di deporre ed eventualmente fucilare il fratello Sebastiano, Leonardo si rifugiò a Nonantola.
Il fratello Sebastiano morì nel 1807, il padre Giovanni l’anno successivo e il figlio Giovanni nel 1811.
Mentre Salimbeni, lieto della caduta di Napoleone sistemava la sua proprietà a Nonantola, il suo secondogenito Sebastiano progettava il palazzo delll’Accademia Tadini a Lovere per lo zio: il conte Luigi Tadini.
Leonardo Salimbeni morì a Modena nel 1823.
RICERCHE SULL’EQUAZIONI DI TERZO GRADO DI LEONARDO SALIMBENI
Il volume di Leonardo Salimbeni, in seguito al frontespizio, presenta una dedica: “A sua eccellenza il signor ANTONIO ZEN Savio di terra ferma alla scrittura.” Salimbeni dona l’operetta ad Antonio Zen, premettendo che il fine del dono non sia la ricerca di Approvazione, poiché non reputa la propria opera importante abbastanza da richiederla; né di Patrocinio, poiché già ne gode; né di Premj, poiché reputa la propria anima abbastanza elevata da non necessitare di una prova fisica delle proprie capacità; né di Difesa, poiché riconosce che ogni autore debba essere in grado di custodire la propria opera senza aiuto esterno. Salimbeni continua il discorso affermando, perciò, che resta dunque che per solo contrassegno di Gratitudine questo tenue dono vi dedichi e consacri. In seguito, ringrazia l’Eccellentissimo Signore per il sostegno ricevuto e giustifica la scelta di donare questo opuscolo con la passione dimostrata da Antonio Zen per gli Studj di Matematica. Salimbeni conclude con lodi ad Antonio Zen.
Seguono dunque la prefazione e gli effettivi capitoli dell’opera
- Capitolo primo: Che tratta di quell’equazioni cubiche che hanno tutte e tre le radici reali sotto forma reale, disuguali e irrazionali
- Capitolo Secondo: Dove si espone un metodo pratico per la risoluzione dell’equazioni numeriche di terzo grado, che hanno tutt’e tre le radici reali.
Il volume si conclude con la “tavola dell’operazione trigonometrica”.



Opera in mostra: Opuscoli di geometria e balistica di Leonardo Salimbeni capitano d'ingegneri e professore di matematica nelle scuole militari di Verona.
In Verona : per gli eredi di Marco Moroni, 1780.
Accademia Tadini, Lovere, Biblioteca storica, ATL H.II.1
OPUSCOLI DI VARIO ARGOMENTO DI GIUSEPPE CASSELLA
Il volume è un unico opuscolo, chiamato anche “Saggio d'un tentativo per risolvere l'equazioni di tutti i gradi”. In questo opuscolo Cassella si dedica alla spiegazione delle sue ricerche, studi e calcoli per trovare un nuovo modo, una nuova formula risolutiva che vada bene per la risoluzione di equazioni di tutti i gradi superiori al terzo, siccome la formula per queste ultime era già stata scoperta nel '500 da Tartaglia.



Opera in mostra: Opuscoli di vario argomento di Giuseppe Cassella regio astronomo della Marina dell'Accademia delle scienze, lettere ed arti di Padova. Opuscolo 1. saggio d'un tentativo per risolvere l'equazioni di tutt'i gradi.
Napoli: nella stamperiadi Pietro Perger, 1788. [due copie]
Accademia Tadini, Lovere, Biblioteca storica, H.II.2
Nel 1534 Gerolamo Cardano, che stava per pubblicare un trattato di Algebra, invita Niccolò Tartaglia a Milano e gli chiede la formula risolutiva delle equazioni di terzo grado.
Tartaglia, che intendeva pubblicarla personalmente dopo aver completato la traduzione del testo di Euclide, trasmette la formula a Cardano nascondendola in un componimento poetico in terzine di endecasillabi, obbligando il collega ad un complicato lavoro per decodificarla.
L’uso di una composizione in rima era comune al tempo, e serviva anche per facilitare la memorizzazione dei passaggi più difficili della formula.
Analisi metrica: Tartaglia scrive la poesia in endecasillabi di terzine incatenate.
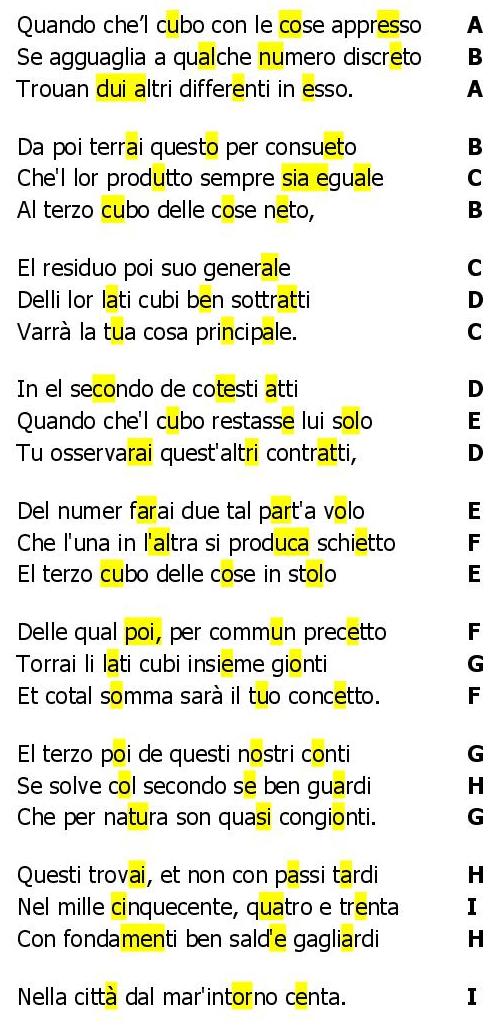
Analisi matematica: Tartaglia scrive in poesia, ma il linguaggio della matematica ora è diverso:

Nella vetrina sono esposte anche due immagini allegoriche:
La PRIMA tratta da un testo di Tartaglia (► vetrina 1) rappresenta la concezione della matematica elaborata da Tartaglia sulla base delle sue riflessioni su Euclide (► vetrina 4)

Nell'incipit del volume esposto nella sezione 1, è rappresentata un'allegoria dei saperi dei quali Tartaglia parla anche nell'incipit della sua traduzione di Euclide.
Viene rappresentato il mondo della conoscenza, definito da due recinti circolari non concentrici a cui si accede attraverso porte che sono sorvegliate da guardiani.
Come precisa lo stesso Tartaglia nella sua edizione di Euclide (esposto nella sezione 4), il primo recinto racchiude le scienze matematiche, l’ingresso è quindi sorvegliato da Euclide stesso che è la chiave di accesso.
All’interno del recinto si trovano le allegorie e le personificazioni delle scienze matematiche: ci sono delle discipline fondamentali che vengono rappresentate per prime (geometria, aritmetica, musica e astronomia) e tutti questi saperi dipendono dalla filosofia che sta in trono nel recinto seguente.
Nicolò Tartaglia viene raffigurato con le scienze ed assiste alla prova di balistica; alle sue spalle ci sono tutti i saperi che dipendono dalla matematica.
Il secondo recinto, quello più elevato, è quello della filosofia, origine di tutte le scienze umane, che viene sorvegliato dell'autorità di Platone ed Aristotele.
La raffigurazione è estremamente ricca di particolari e viene attribuita a Giovanni Antonio Rusconi, un giovane ingegnere, architetto e disegnatore veneziano, allievo di Tartaglia.
La SECONDA, tratta da una delle edizioni dell’Iconologia di Cesare Ripa, presenta, un’immagine allegorica della scienza matematica con una serie di oggetti che servono per indicare i suoi scopi e le sue finalità.
![]()

Donna di mezza età, vestita di velo bianco e trasparente, con l’ali alla testa, le trecce siano distese giù per le spalle, con un compasso nella destra mano, mostri di misurare una tavola segnata da alcune figure e numeri, e sostentata da un fanciullo al quale ella mostri di parlare insegnandoli, con l’altra mano terrà una palla grande figurata per la terra con il disegno dell’hore, e circoli celesti, e nel lembo della veste sia un fregio intessuto di figure Mathematiche, siano i piedi ignudi sopra una base.
Opera in mostra: Noua iconologia di Cesare Ripa perugino caualier de ss. Mauritio, & Lazzaro. Nella quale si descriuono diuerse imagini di virtu, vitij, affetti, passioni humane, arti, discipline, humori, elementi, corpi celesti, prouincie d'Italia, fiumi, tutte le parti del mondo, ed altre infinite materie. Opera utile ad oratori, predicatori, poeti, pittori, scultori, disegnatori, e ad'ogni studioso per inuentar concetti, emblemi, ed imprese ... ampliata vltimamente dallo stesso auttore di trecento imagini, e arricchita di molti discorsi pieni di varia eruditione; con nuoui intagli, & con molti indici copiosi...
In Padoua : per Pietro Paolo Tozzi : nella stampa del Pasquati, 1618.
Accademia Tadini, Lovere, Biblioteca storica, ATL G.IV.36
 Niccolò Fontana, noto come Niccolò Tartaglia, nacque a Brescia nel 1499, rimase orfano di padre all'età di 6 anni. Il 19 febbraio 1512 l'esercito francese, guidato da Gaston de Foix, durante il sacco di Brescia aggredì un gruppo di donne e bambini rifugiatisi nel Duomo della città, Niccolò subì ferite profonde alla mascella e al palato e sua madre bagnò le sue ferite con acqua, non potendosi permettere alcun medicinale. Egli guarì ma, a causa delle ferite riportate che il matematico nascondeva con la folta barba, divenne balbuziente e perciò gli venne assegnato il soprannome di 'tartaglia', che accettò, e con il quale firmò tutte le sue opere. Malgrado non avesse frequentato studi regolari, il suo talento per la matematica e il suo genio gli permisero di ottenere grandi successi accademici.
Niccolò Fontana, noto come Niccolò Tartaglia, nacque a Brescia nel 1499, rimase orfano di padre all'età di 6 anni. Il 19 febbraio 1512 l'esercito francese, guidato da Gaston de Foix, durante il sacco di Brescia aggredì un gruppo di donne e bambini rifugiatisi nel Duomo della città, Niccolò subì ferite profonde alla mascella e al palato e sua madre bagnò le sue ferite con acqua, non potendosi permettere alcun medicinale. Egli guarì ma, a causa delle ferite riportate che il matematico nascondeva con la folta barba, divenne balbuziente e perciò gli venne assegnato il soprannome di 'tartaglia', che accettò, e con il quale firmò tutte le sue opere. Malgrado non avesse frequentato studi regolari, il suo talento per la matematica e il suo genio gli permisero di ottenere grandi successi accademici.
Si trasferì a Verona nel 1521, e successivamente a Venezia, per insegnare matematica. Acquisì la sua notorietà a seguito della disfida proposta dal matematico Antonio Maria Del Fiore, discepolo di Scipione dal Ferro, che vent'anni prima aveva risolto le equazioni cubiche senza però svelarne il metodo risolutivo. Tartaglia risolse tutti i quesiti di Del Fiore in un paio d'ore, mentre l'avversario non ne risolse nessuno.
Era il 1534: due matematici milanesi, Gerolamo Cardano e l'allievo Ludovico Ferrari, chiesero a Nicolò di pubblicare in un libro le sue scoperte, ma Tartaglia rifiutò. Niccolò rivelò in seguito la formula a Cardano, con la promessa di non utilizzarla.
Tuttavia, Cardano venne a conoscenza della formula risolutiva scoperta precedentemente da Scipione Dal Ferro, e reputandola identica a quella di Tartaglia si ritenne sciolto dal giuramento.
Pubblicò la formula risolutiva dell'equazione di terzo grado, nota ancora oggi con il nome di Cardano-Tartaglia.
Niccolò Tartaglia, che nel frattempo aveva per primo tradotto gli Elementi di Euclide in italiano e trattato in più opere di balistica, geometria, algebra, artiglieria, fortificazioni e strategia, perse nel 1548 una disfida contro Ludovico Ferrari intento a difendere il suo mentore. Tornato a Venezia nel 1551 ideò un sistema che con l'ausilio di cordami permetteva di recuperare navi affondate tuttavia ebbe scarso successo. Nel libro del 1556, General trattato di numeri et misure, introduce il triangolo di Tartaglia, che riteneva una sua scoperta ma che in realtà era già noto agli arabi e ai cinesi. Morì a Venezia il 13 dicembre 1557.
Opera in mostra: Opere del famosissimo Nicolo Tartaglia cioé Quesiti, Trauagliata inuentione, Noua scientia, Ragionamenti sopra Archimede. Nelle quali copiosamente si spiega. L'arte di guerreggiare, cosi in mare, come in terra, ... - In Venetia : al segno del Lione, 1606.
Accademia Tadini, Lovere, Biblioteca storica, ATL G.II.15
La biblioteca dell'Accademia Tadini ospita una sezione dedicata ai libri di matematica. Tra questi, le professoresse Carolina Bergamini e Daniela Molinari hanno individuato un piccolo nucleo di volumi che consente di ricostruire la storia del matematico bresciano Niccolò Fontana, detto Tartaglia (Brescia, 1499 circa - Venezia, 13 dicembre 1557). Su questo tema hanno lavorato, nell'ambito di un Percorso per le Competenze Trasversali e l'Orientamento (PCTO), quattro studienti del quarto anno del Liceo Classico - Samuele Balduzzi, Camilla Coronini, Dariia Kravchenko, Elisa Saporiti - che hanno curato questa esposizione, con la supervisione del dott. Marco Albertario, direttore dell'Accademia.
Niccolò Tartaglia: una vita di sfide
La matematica tra poesia e immagine
Dopo Euclide: geometria e balistica
