La poliedrica Trieste
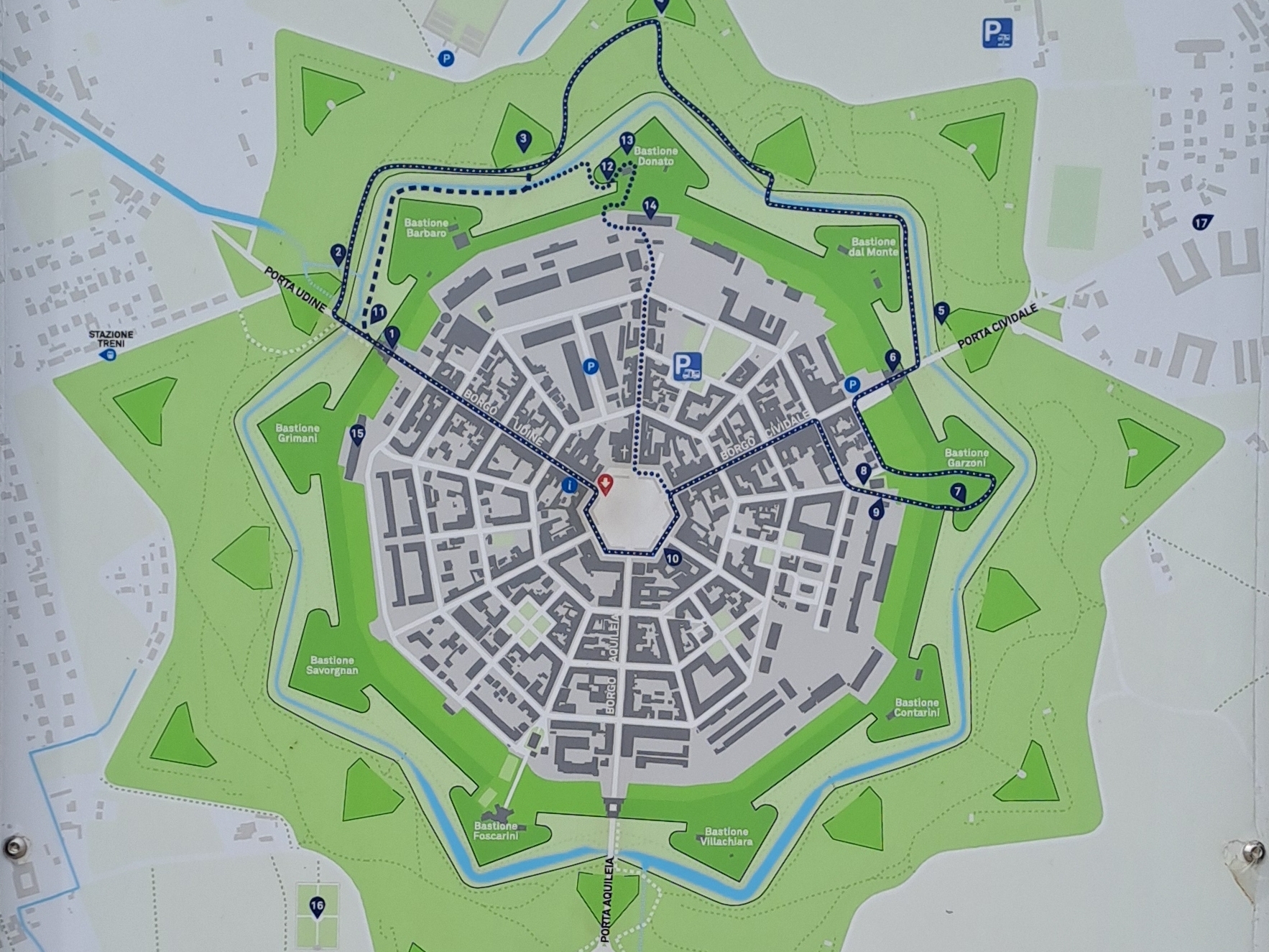
Mi piace organizzare viaggi per le mie classi, perché mi piace mostrare la matematica attorno a noi, nella realtà. Quando scelgo una meta, comincio, quindi, dalla matematica o dalla fisica, perché visitando una città si è immersi, consapevolmente, nell’arte e nella storia, ma si dimentica la componente scientifica, meno visibile, o forse visibile solo per gli occhi più allenati. L’ultima scelta è stata Trieste, ma, durante il viaggio di andata, abbiamo scelto di fermarci prima a Palmanova, la città-fortezza, con la sua stella a nove punte e il suo lato di 400 m che garantiva la possibilità per i cannoni della città di gestire la difesa, mentre il muro inclinato smorzava la potenza dei cannoni nemici, come è stato spiegato nel video di Geopop. Le strutture difensive della città ci hanno regalato degli scorci piacevoli, visto il cielo sereno, che mostrava un bel contrasto con il verde della vegetazione primaverile.


Al centro della città c’è una piazza esagonale, centro proprio della ragnatela, costituita dalle vie che partono a raggio e che si sviluppano in poligoni regolari concentrici. Nelle mura si aprono tre porte e le strade che passano attraverso esse si incontrano nel centro della piazza formando angoli di 120°, in una manifestazione di simmetria che diventa bellezza.

La seconda sosta è stata il Santuario Mariano del Monte Grisa, che domina la città di Trieste e permette, quindi, di vedere la città dall’alto, in un assaggio di ciò che ci aspetta. La struttura in cemento armato è tipica dell’architettura brutalista, che si è sviluppata in Inghilterra negli anni Cinquanta del secolo scorso. Il triangolo è la struttura modulare che si ripete sempre uguale, ma è un triangolo isoscele particolare, con la base uguale all’altezza, ovvero inscrivibile in un quadrato e con un lato obliquo che ha misura pari a metà del lato moltiplicato per radice di 5. Il triangolo ha una forte valenza simbolica per la fede cristiana, richiamando la trascendenza e la Trinità, ma in questo caso va oltre, ricordando la struttura di un alveare e proponendo una A, facilmente visibile, e una M (che ho faticato a far cogliere ai miei alunni), che sono le iniziali di Ave Maria, la celebre preghiera cattolica.


All’interno del Santuario ci sono due chiese, una sopra l’altra e passare da quella superiore a quella inferiore fa sentire schiacciati: come quella superiore fa sentire lo slancio verso l’alto, quella inferiore fa sentire il peso della gravità, e realizza l’intento dell’ingegnere Antonio Guacci, visto che sembra davvero di trovarsi nella stiva di una nave.

Giunti in città, nonostante il maltempo, abbiamo fatto un breve percorso per entrare in contatto con l’anima letteraria della città, quella più nota, quella presente negli antichi caffè letterari e nelle statue di Joyce, Saba, D’Annunzio e Svevo. Visto che il nostro albergo era nel quartiere teresiano, la nostra prima tappa è stato il Canal Grande, dove abbiamo incontrato James Joyce. Su questo canale si affacciano il Tempio Serbo-Ortodosso di San Spiridione e la Chiesa di Sant’Antonio Nuovo, come esempio dell’anima poliedrica della città, che non è solo il punto di incontro di tradizioni diverse - la Slovenia, l’Italia e l’Austria - ma è anche l’incrocio di religioni diverse. Il passo successivo è stato la statua di Umberto Saba, in via Dante Alighieri: il povero poeta è stato privato della pipa, spesso rubata, ma anche del bastone, ma è stato facile immaginarlo percorrere le strade cittadine mentre si dirigeva verso la sua libreria, esempio di ciò che hanno vissuto gli ebrei con le leggi razziali.
Inoltrarsi nella città ha significato anche raggiunge la sua anima più antica, con il Teatro romano, che con la sua apertura semicircolare e i suoi gradoni non può che richiamare la matematica! Piazza della Borsa, il “secondo salotto buono cittadino”, ci ha accolto con la sua eleganza (anche se a me il timpano con l’orologio del Palazzo della camera di commercio ha ricordato l’orologio di Hill Valley in Ritorno al Futuro) e Gabriele D’Annunzio non poteva che starsene elegantemente seduto su una panchina (questa statua è stata ribattezzata la “statua della discordia”). L’ultimo luogo della giornata è stato Piazza Unità d’Italia, con la sua Fontana dei quattro continenti sormontata dalla statua alata che rappresenta la città di Trieste. La Fontana è un simbolo della rinascita della città, visto che era stata spostata per consentire il discorso del Duce, che annunciava la promulgazione delle leggi razziali, ed è stata rimessa al suo posto solo in tempi recenti: è stato facile farsi portare indietro nel tempo, pur cercando di sostituire quel ricordo amaro con quello del presidente Luigi Einaudi, che il 4 novembre del 1954, insieme al sindaco della città, ha aperto i festeggiamenti per il ritorno di Trieste all’Italia.


Il suo ritorno alla normalità in tempi così recenti ha ricordato a tutti che Trieste è la città che è solo da poco tempo e che le ferite che ha subito durante la Seconda guerra mondiale forse non sono ancora del tutto rimarginate. La sosta al Santuario Mariano ci aveva permesso di cogliere questa sofferenza, perché non è possibile visitare il santuario senza ricordarne la nascita, con la risposta di Mons. Santin allo Stato maggiore tedesco: «Si stanno avvicinando da due parti gli eserciti. Resistere per farsi ammazzare e per distruggere Trieste? Questa città è la porta d’Europa centrale; perché distruggerla senza alcun scopo? Non è una città germanica; voi, tedeschi, pensate a difendere quelle. Questa è una città italiana, e gli italiani non avrebbero mai dimenticato.» (27 aprile 1945) Dopo aver individuato tutti i palazzi che si affacciano sulla Piazza, dopo aver raccontato della torre campanaria e dei due mori Micheze e Jacheze, e averli sentiti scandire il trascorrere del tempo, abbiamo volto lo sguardo al mare, il quarto lato della piazza, a significare l’apertura della città al mondo.
L’Immaginario Scientifico è stato il punto focale del secondo giorno di visita, visto che l’intero viaggio è stato costruito attorno alla disponibilità del museo: la visita è andata ben oltre le aspettative di noi insegnanti, visto che al termine della mattinata è stato difficile allontanare i ragazzi, che si sono mostrati coinvolti e incuriositi, entusiasti delle attività, delusi da quella che è sembrata una permanenza troppo breve. Durante la visita, abbiamo affrontato il percorso sull’energia con un laboratorio che ha permesso di focalizzare l’attenzione sulle energie rinnovabili, realizzando l’elettrolisi e studiando il funzionamento dei pannelli fotovoltaici, variandone l’inclinazione e la distanza rispetto alla fonte di luce e calore, e attraverso l’inserimento di filtri colorati.



La seconda parte del percorso ha visto come protagonisti i vari exhibit che hanno permesso ai ragazzi di toccare con mano la scienza, di sperimentarla in prima persona, esplorando e divertendosi. La prima parte del percorso ha permesso a tutti di cogliere la centralità della scienza nella città di Trieste, a partire dalla figura di Paolo Budinich, che insieme ad Abdus Salam, fondò a Trieste il Centro internazionale di fisica teorica. Con la prima mappa, topologica, i ragazzi hanno potuto vedere i collegamenti tra i vari scienziati, il loro ruolo nel Sistema Trieste, la presenza di un esiguo numero di donne, ma l’importanza della ricerca scientifica in questa città, visto che se la media in Italia è di 5 ricercatori ogni 1000 persone, a Trieste è di 37. Il piano superiore della struttura ha permesso di esplorare la matematica con il gioco: tassellazioni e puzzle, serie di Fibonacci, cubi di binomi e quadrati di trinomi, simmetrie con la simpatica scrittura allo specchio, la camera oscura, le illusioni ottiche… insomma, così tanta matematica da lasciare inebriati!


La meta successiva, nel pomeriggio, è stata la Grotta Gigante: la grotta non è solo magnificenza e bellezza indescrivibile, ma anche laboratorio scientifico, come ci ricordano i due pendoli centrali, usati per le rilevazioni sismiche.


La giornata si è conclusa con un ulteriore giro in città: ci siamo fatti lasciare alla Cattedrale di San Giusto, in cui il rosone centrale ha rimandato alla matematica (ovviamente!), ma ha anche evidenziato la mancanza di simmetria della struttura. Una mancanza presente anche all’interno, visto che le colonne che separano le navate sono spaziate in modo diverso ai due lati dell’altare. I ragazzi hanno notato questa rottura della simmetria, evidenziandola come mancanza di bellezza!


Dopo la salita al castello per vedere da vicino i due automi originali, Micheze e Jacheze,

siamo ridiscesi lungo la strada antistante la cattedrale, verificando la distanza in passi dall’Arco di Riccardo. Ci siamo soffermati sul nome dell’arco, ma la mancanza di simmetria (successiva alla sua costruzione) è stata poco notata: i ragazzi cominciavano a scalpitare, assaporando il momento di libertà che abbiamo concesso loro dopo aver raggiunto l’inetto triestino, Italo Svevo.


L’ultimo giorno di visita è stato un’oscillazione tra presente e passato, avendo scelto di lasciare ampio spazio ad entrambe le anime della città: abbiamo visitato l’Area Science Park di Padriciano, all’origine un campo profughi, dove i ricercatori Alessandro e Pietro, insieme allo studente della magistrale di fisica Nicolò, ci hanno guidato alla scoperta dei lavori che vengono svolti all’interno dei laboratori dell’INFN. Dopo averci parlato della fisica delle particelle e averci tratteggiato il quadro storico, estendendo il discorso fino al CERN, hanno permesso ai nostri studenti di capire cosa significhi studiare le particelle, anche attraverso il confronto tra le strumentazioni in uso nel passato e quelle più moderne. In una sala riunioni, gli studenti hanno poi potuto fare domande, in un piccolo percorso di orientamento.


La seconda parte della mattinata ha avuto per protagonista il Monumento Nazionale delle Foibe di Basovizza. Lo storico che ci ha accompagnato in questo percorso ha fatto in modo che potessimo cogliere nei particolari la storia più recente della città, a partire dalla fine della Prima guerra mondiale fino ai giorni nostri. Il passato delle foibe è un passato che è ancora presente, se pensiamo anche solo a quanto ci ha raccontato lo storico della sua esperienza: quando fa la guida a Basovizza viene etichettato come fascista e quando si ritrova a fare la guida alla Risiera di San Sabba viene etichettato come comunista. La riflessione che è stata sollecitata è andata ben oltre i luoghi visitati e il tempo studiato, mentre il monumento, con le sue linee scarne ed essenziali, ha richiamato le macchine della fisica che avevamo visto in piazza a Palmanova: in quel caso erano servite per costruire le fortificazioni della città, in questo sono state utilizzate per calarsi all’interno della foiba a carpirne i segreti. Questa comunicazione tra interno della foiba e mondo esterno è stata bloccata da un coperchio che, con la sua fissità e la ruggine, dà l’idea di un evento fermo nel tempo, lontano ma al tempo stesso vicino.


La visita alla città di Trieste ci ha permesso di notare come il linguaggio della matematica, astratto e simbolico, possa essere lo strumento ideale per comunicare attraverso i simboli, basti pensare al Santuario Mariano del monte Grisa. Il rigore della matematica, inoltre, può diventare espressione di regolarità e bellezza, presente in Piazza Unità d'Italia, è stata manifestazione di eleganza e maestosità, mentre la sua assenza, come nella Cattedrale di San Giusto, ha segnalato una mancanza di armonia. Mi ha colpito il fatto che Trieste sia nominata soprattutto come città letteraria, mentre la sua essenza è, ancora una volta, più articolata e poliedrica di quanto sia possibile cogliere con un primo sguardo: Trieste è una città scientifica, e spesso il turista medio coglie “solo” la bellezza artistica, senza rendersi conto che l’arte sceglie la matematica per enfatizzare certi aspetti. Federica Manzon, nella guida di Trieste del Touring Club, scrive: «A scuola ci insegnavano le poesie di Rilke che a Duino inseguiva l’Angelo del Tempo, poi Svevo ovviamente e ci portavano in visita alla libreria antiquaria del poeta [Saba]. Nei caffè non mancavano mai le presentazioni di qualche autore cittadino, meglio se poco noto nella nazione. Così una generazione dopo l’altra è cresciuta nel culto della città di carta e la letteratura è considerata patrimonio del Dna triestino: un mito tutto rivolto al passato, un culto dei morti poco celebrati in vita. Passa invece del tutto sotto silenzio la presenza in città di uno degli avamposti scientifici più importanti al mondo.» Così Trieste, connubio di tradizioni (Slovenia, Austria, Italia), incontro di religioni, diventa anche culla delle “due culture”, l’anima umanistica e quella scientifica, che ognuno di noi porta dentro di sé, ne sia consapevole oppure no.
Durante la costruzione del percorso di visita ho letto dell’impegno di Abdus Salam, quello che Pietro Greco definisce il pakistano visionario, che «propose di allestire un centro dove formare alla fisica teorica i giovani più valenti dei paesi in via di sviluppo. Non solo per il valore culturale intrinseco di una simile iniziativa, ma anche perché la scienza è il motore dello sviluppo economico. E la scienza di base è il primum movens della scienza. In altri termini – questo era il pensiero di Abdus Salam, in controtendenza rispetto a molto analisti – i paesi in via di sviluppo non possono fare a meno di eccellere anche nelle scienze più astratte se vogliono recuperare il gap economico che li separa dai paesi più avanzati.». Ci è stato fatto notare come l’eccellenza di Trieste sia diversa dall’eccellenza americana: per accedere alle grandi università statunitensi, devi dimostrare di essere all’altezza, mentre Trieste apre le proprie porte a chi questo sapere lo vuole costruire, per portarlo poi nel proprio paese di origine, per permettere anche ai paesi meno fortunati di costruirsi un futuro.
Fotografie realizzate durante il viaggio di istruzione a Trieste, il 17, 18 e 19 aprile 2024, con le classi 3AS e 3ES.
Padova matematica
La scelta di visitare Padova, con una seconda liceo scientifico, non è certo stata casuale, considerati i 18 anni che Galileo Galilei ha passato in questa città (i migliori della sua vita*). Padova può, quindi, essere considerata la culla della scienza moderna e, visto che in seconda liceo scientifico in fisica si affronta lo studio della cinematica, che si completa poi, nella seconda parte dell’anno, con la dinamica, Padova diventa una tappa obbligata.
Il passaggio da Palazzo Bo è stato il primo passo alla scoperta di questa città, in un percorso che si è arricchito di matematica ad ogni passo.
A Palazzo Bo abbiamo avuto modo di visitare il teatro anatomico, con la sua struttura ellittica a cono rovesciato, come un anfiteatro romano, con sei ordini concentrici. Ripensando alle dimensioni della struttura, non si può non rimanere colpiti dall’illusione ottica che fa percepire il teatro come se fosse più piccolo. Le sei ellissi accoglievano gli studenti che dovevano assistere alle autopsie e potevano contenere fino a 250 spettatori.


Il teatro anatomico fotografato dal basso verso l’alto, e il modellino presente nell’anticamera, che permette di coglierne l’intera struttura.
L’ellisse ci ha accolto anche a Prato della Valle, dove ci siamo recati per un pranzo sul prato: con i suoi 90.000 m2 è una delle piazze più grandi d’Europa e le 88 statue (in realtà, dopo il passaggio di Napoleone, 78) permettono di incontrare il matematico Giovanni Poleni e anche Galileo Galilei, al quale manca il dito medio della mano destra.


La statua n° 36, raffigurante Galileo Galilei, e uno scorcio del canale che delimita il parco
Purtroppo, la struttura di Prato della Valle si può cogliere bene solo osservandola dall’alto, e per quanto sia stato meraviglioso il panorama che abbiamo goduto dalla Specola, il nostro sguardo non ha potuto raggiungere Prato della Valle.



La Specola di Padova è stata sede dell'Osservatorio Astronomico ed è ora una delle più importanti strutture di ricerca dell'Istituto Nazionale di Astrofisica. Nella Sala della Meridiana, abbiamo potuto ammirare le ellissi delle orbite dei pianeti (tra i quali, vista l’antichità del dipinto, mancano Urano e Nettuno – insieme a Plutone, pianeta-nano) nell’affresco del sistema solare. Non può mancare, nella stessa sala, l’analemma (più propriamente lemniscata) che, con la sua forma a 8 deformato, descrive la posizione del Sole nei diversi giorni dell’anno.


L’affresco del Sistema Solare e la meridiana tra i piedi degli studenti

Dalle ellissi alle circonferenze il passo è breve, visto che la circonferenza è un’ellisse con i fuochi coincidenti. Nella Sala delle Figure, sulle pareti troviamo rappresentati, a figura intera, otto scienziati, Tolomeo, Copernico, Tycho Brahe, Galileo, Keplero, Newton, Montanari e Poleni. Secondo quanto riportato nella nota numero 9 di questo lavoro di Valeria Zanini, L'eredità scientifica e culturale di Giuseppe Toaldo, a 300 anni dalla nascita, «Giovanni Santini (1787-1877), terzo direttore dell’Osservatorio, decise che la volta fosse ridipinta con una serie di cerchi concentrici di stelle su sfondo azzurro. Tutto attorno furono dipinte, in medaglioni, le effigi di sedici celebri astronomi e matematici: Ipparco, Tolomeo, Copernico, Galileo, Keplero, Cassini, Newton, Maraldi, Bradley, Herschel, Lagrange, Laplace, Bessel, Gauss, Piazzi, Oriani.» Anche il quadrante presente nella Sala delle Meridiane riporta alla circonferenza, trattandosi di un quarto di cerchio, ma ce n’è uno anche nella Sala delle Figure.



Con le sue cupole e i suoi rosoni, anche la Basilica del Santo ci parla di circonferenze.
A Palazzo Bo abbiamo ritrovato anche una spirale, nella stele di Giò Pomodoro dedicata a Galileo Galilei, ma la spirale ha dominato anche tra fossili, ammoniti e chiocciole al Museo della Natura e dell’Uomo, lungo il percorso Evolution-Revolution.


All’inizio della nostra visita guidata al museo, ci siamo imbattuti in una lemniscata (o in un simbolo di infinito, se preferite) come a farci presente, fin da subito, che il percorso dell’evoluzione non avviene in linea retta. Al tempo stesso, le dimensioni ci hanno permesso di notare come l’uomo costituisca solo un piccolo tassello, visto che occupa un piccolo segmento nel Quaternario.

Della nostra visita a Palazzo Bo vanno sottolineate, in chiusura, due cose: la prima è la statua di Elena Lucrezia Cornaro Piscopia, prima donna al mondo a ottenere una laurea, il 25 giugno del 1678. Un ricordo di lei è presente anche nella Cattedrale, in quanto oblata benedettina. Citando la voce a lei dedicata su Wikipedia: «Figlia di un nobile della Repubblica di Venezia che ne favorì in tutti i modi l'educazione, a diciannove anni prese i voti come oblata benedettina, proseguendo gli studi di filosofia, teologia, greco, latino, ebraico e spagnolo. Ormai nota agli studiosi del tempo, a partire dal 1669 fu accolta in alcune delle principali accademie dell'epoca. Quando il padre chiese che la figlia potesse laurearsi in teologia all'Università di Padova, il cardinale Gregorio Barbarigo si oppose duramente, in quanto riteneva "uno sproposito" che una donna potesse diventare "dottoressa", perché avrebbe significato "renderci ridicoli a tutto il mondo".»
L’ultimo ricordo che portiamo con noi, al termine di questa visita, è la Scala del Sapere di Gio Ponti: rappresenta il cammino della conoscenza di ogni studente durante la sua carriera e il termine, «Ancora imparo», in cima alla scala – dove ritroviamo uno studente ormai anziano che non è più nemmeno in grado di reggere i libri – ricorda a tutti noi che la vita stessa è un percorso di apprendimento che non ha mai fine.


Questo è solo un assaggio di ciò che si può trovare a Padova: c'è anche molto altro, come ho scoperto nel libro La scienza nascosta nei luoghi di Padova, presentata come "geografia scientifica urbana" da Telmo Pievani.
* Galileo Galilei si è trovato così bene a Padova, che qualcuno ha deciso per lui che dal 2 agosto 1823 la sua quinta vertebra lombare, donata dal medico vicentino Domenico Thiene, venisse conservata proprio a Palazzo Bo.
Fotografie realizzate durante la visita di istruzione a Padova, il 3 aprile 2024, con la classe 2AS.
Problemi aprile 2024 - 2
Verifica di matematica, classe seconda liceo scientifico
Argomento: problemi risolvibili algebricamente, equazioni di secondo grado parametriche
Durata: 120 minuti
Problemi aprile 2024
Verifica di matematica, classe seconda liceo scientifico
Argomento: problemi risolvibili algebricamente, equazioni di secondo grado parametriche
Durata: 120 minuti
Inesauribile caparbietà
Ho pochi ricordi del mio rapporto con la matematica alla scuola primaria, forse perché mi veniva facile e naturale, ma mi è rimasto impresso il disegno alla lavagna di un trapezio e la sua trasformazione in un triangolo equivalente, a spiegare perché per calcolare l’area fosse necessario sommare le basi e moltiplicarle per metà altezza. Forse in quel momento mi sono innamorata della geometria.
I ricordi più vividi sono quelli della scuola media: ricordo quando il professore assegnava delle espressioni da svolgere e le proponeva come sfida alla classe, tanto che in quei momenti, quando capitava che due persone si alzassero nello stesso momento, si assisteva a vere e proprie gare di corsa per raggiungere prima la cattedra. Ricordo, in particolare, che a volte arrivavi alla cattedra, soddisfatto del tuo lavoro e trepidante, ma il professore scuoteva la testa guardando il risultato e allora tornavi al tuo banco per riprovare, intestardendoti alla ricerca della strada corretta.
Del percorso liceale ricordo che l’errore in matematica ha cominciato a presentarsi con una maggiore frequenza, se penso ai problemi di geometria euclidea e analitica o di trigonometria, magari con tanto di discussione e sistemi parametrici al seguito. Capitava di intestardirsi su un problema che non dava il risultato corretto: al mattino, condividevo la mia frustrazione con mia cugina, che era in una classe parallela alla mia, e mi confrontavo con lei, che magari stava litigando con lo stesso problema (avevamo lo stesso insegnante) e ne parlavamo, ripercorrendo insieme le fasi della soluzione, mentre camminavamo verso la scuola. A volte succedeva che trovassimo la soluzione prima di arrivare in aula, e trascrivere i passaggi sul quaderno era solo la conferma di quanto avevamo già capito lungo il cammino. Altre volte, ancora, mi capitava di continuare a pensare al problema durante tutto il pomeriggio, senza riuscire a trovare una soluzione, ma al mattino mi svegliavo con la consapevolezza di conoscere quella soluzione e, prendendo in mano carta e penna, verificavo i passaggi, prima ancora di essere completamente sveglia: è stato in quel momento che ho capito l’importanza del “dormirci su”. Ancora adesso, con maggiore consapevolezza, se ho un problema che non riesco a risolvere (che sia di matematica o di altro) ci penso un attimo prima di addormentarmi, perché la mia testa possa continuare a lavorarci mentre riposo. È la stessa strategia che suggerisco ai miei alunni (per quanto, durante una verifica sia un po’ più difficile riuscire a “dormirci su”…). Mi fa ripensare a Poincaré che, dopo essersi concentrato a lungo e inutilmente su un problema, decise di partire per un gita e, mettendo piede sull’omnibus di Coutances, riuscì a trovare la soluzione (secondo il racconto fatto nel libro Le ostinazioni di un matematico, che racconta l’originale storia di Armand Duplessis, che avrebbe sprecato la propria vita nel tentativo di dimostrare la congettura di Goldbach).
Credo si sia colto il comune denominatore di questi tentativi: la testardaggine… e se penso al percorso universitario, questa mia caratteristica ha avuto un ennesimo banco di prova. Mi sono ritrovata nelle parole di Roberta Fulci che, durante la diretta con Ilaria Fanelli, Una matematica a Radio3 Scienza, ha risposto alla domanda di uno spettatore che chiedeva di essere rassicurato in merito alle sue difficoltà universitarie: Roberta ha raccontato che, avendo scelto matematica dopo il liceo classico, si è trovata ad affrontare grandi difficoltà durante il primo anno di corso ed ha avuto la sensazione di passare “dall’essere brava all’essere un rapa”. Come al solito, Roberta ha espresso il concetto in modo colorito e simpatico, come è tipico suo, e io ho capito perfettamente cosa intendesse, perché l’ho provato sulla mia pelle, anche se avrei dovuto essere più facilitata di lei, visto che alle spalle avevo un liceo scientifico! In realtà, arrivare alla fine del mio percorso universitario, alla tanto desiderata laurea in matematica, ha richiesto un bel po’ di caparbietà, tanto che a chi mi chiedeva che cosa avessi imparato dal mio percorso universitario rispondevo: “Ho imparato ad abbattere i muri a testate”.
Ho concluso il percorso universitario, nonostante… nonostante tutto! Per questo, forse, ho sempre ritenuto la caparbietà una componente fondamentale della buona riuscita in matematica. Addentrandomi sempre più nella storia della matematica, ho scoperto che essa è costruita sulla determinazione, sulla tenacia, sulla caparbietà. Uno dei primi libri che ho letto è L’ultimo Teorema di Fermat di Simon Singh: i tentativi di dimostrare il teorema si dipanano lungo i secoli, dando luogo a una staffetta espressione di un lavoro corale, come se ognuno dei matematici che ha preso parte a questo percorso avesse contribuito alla soluzione del puzzle apportando la propria piccola tessera, fino ad arrivare al risultato finale di Andrew Wiles. Per questo, forse, si parla di comunità matematica, pensando a quelle occasioni in cui i singoli matematici concentrano tutti le proprie forze per raggiungere un obiettivo comune, attraverso un lavoro continuo.
La mia convinzione che determinazione e caparbietà possano essere un’arma vincente anche a scuola mi ha portato a proporre, all’inizio di ogni percorso scolastico, una citazione di John Wooden, uno dei più grandi allenatori nella storia del basket delle università americane:
«Quando si migliora un po’ ogni giorno, alla fine si raggiungono grandi risultati. Quando si aumenta l’allenamento giorno dopo giorno, si ottiene un netto miglioramento della forma fisica. Non sarà domani, né dopodomani, ma poi i progressi saranno notevoli. È inutile puntare a grandi risultati in tempi brevi, conviene invece cercare di migliorare un po’, un giorno dopo l’altro. È l’unico modo per ottenere risultati duraturi.»
Gigliola Staffilani, prima donna italiana full professor al MIT, alla domanda rivoltale da Roberto Natalini in un’intervista del 2018 «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?» ha dato una bella risposta: «Credo che l’intuizione arrivi quando ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte.» Secondo la leggenda, pare che al re Tolomeo, che chiedeva un metodo rapido per studiare la geometria, Euclide abbia risposto che non esistono “vie regie”, ovvero percorsi privilegiati: in altre parole, ci sono stati matematici grandissimi nella storia, ma questo non significa che per loro le cose siano state più facili, perché avevano talento. Il duro lavoro resta una componente fondamentale per la buona riuscita in matematica!
Nei giorni scorsi, durante una lezione nella mia terza liceo scientifico, mentre le idee continuavano ad accumularsi intorno al tema della caparbietà, ho chiesto ai miei alunni quale potesse essere la caratteristica che una persona deve possedere per garantirsi un successo in matematica. Sono rimasta molto colpita dalle loro risposte: innanzi tutto perché molti di loro, invece di indicarmi una caratteristica, hanno risposto fornendo una strategia, che passava attraverso il ragionamento, la comprensione o la spesa di un po’ di tempo per creare collegamenti mentali, ma qualcuno ha risposto: «bisogna sapere le regole per poterle applicare meccanicamente» e, davanti alle mie proteste, si è difeso parlando di una strategia personale. Mi ha colpito, inoltre, che qualcuno ritenga importante il calcolo o “farsi piacere la matematica”, perché se è vero che, per certi aspetti, l’apprendimento è reso più facile dalla passione, non è certo possibile imporsi a comando di amare una disciplina. Dopo aver indicato la necessità di fare molti esercizi, qualcuno ha parlato di perseveranza e costanza, della capacità di non abbattersi per un risultato negativo, di forza di volontà e determinazione… e poi c’è il mio foglietto con scritto: caparbietà.

Ho voluto approfittare di queste risposte per riflettere con loro, a partire dalla storia di Sophie Germain (è mia intenzione partecipare a #peopleformath2024 lanciato dal canale IlariaF Math…). La sua vicenda biografica ha tutte le caratteristiche di un romanzo, con l’assunzione dell’identità di Antoine Le Blanc, per poter interloquire con i matematici più importanti dell’epoca come Lagrange e Gauss, e per approfondire la sua vita ho fatto riferimento al libro di Cecilia rossi Sophie Germain. Libertà, uguaglianza e matematica.

Al momento di costruire una bibliografia, mi sono imbattuta anche in Nothing stopped Sophie, di Cheryl Bardoe, con le illustrazioni di Barbara McClintock: si tratta di un libro per bambini, disponibile solo nella versione inglese, nel quale troviamo, ripetuto più volte, “Nothing stopped Sophie”, perché effettivamente niente riuscì a fermarla! Nel momento in cui i suoi genitori hanno cercato di ostacolarla nella sua passione per la matematica, lei ha trovato il modo di andare avanti, ad esempio.

Le donne che hanno scritto di lei considerano la caparbietà uno dei suoi lati più positivi, ma non è così se la sua vicenda viene interpretata da uomini: nel libro Il genio delle donne, Piergiorgio Odifreddi ha dedicato alla Germain il capitolo La prima vera matematica, ma non le risparmia il suo sarcasmo, visto che la definisce una giovane dal «carattere difficile e [dai] modi arroganti». Parlando poi del suo scontro con l’astronomo Joseph de Lalande, che l’aveva omaggiata del suo “Astronomia per le dame”, una delle pubblicazioni dell’epoca che trattava le donne con condiscendenza e proponendo una divulgazione in versione semplificata, dice che lei «disdegnava i testi divulgativi, e rivolse presto la sua attenzione alle difficili Disquisizioni aritmetiche», come se in realtà Sophie Germain peccasse di presunzione e non fosse realmente in grado di comprendere un testo del genere. Come insegnante ho imparato a considerare la presunzione e l’arroganza una necessità, per i giovani: senza presunzione, non potrebbero mettere in dubbio i tanti “ipse dixit” con i quali si trovano a confrontarsi quotidianamente, e senza un po’ di arroganza non avrebbero il coraggio di competere con gli adulti. Franco Pastrone, del Dipartimento di matematica dell’Università di Torino, nel suo intervento per l’Associazione Subalpina Mathesis, che è diventato l’introduzione nel libro di Maria Rosa Menzio Il Signor Le Blanc, ha un giudizio a tratti tranchant: riferendosi all’infanzia, parla di episodi «forse un po’ forzati al fine di esaltare la determinazione della ragazza», che descrive come una persona timida in pubblico, anche se, quando si trattava di ottenere dei risultati scientifici «la sua timidezza scompariva, anzi riusciva a mostrare una cocciuta aggressività».
Mi è parso quasi di cogliere che questa caparbietà, così positiva quando esercitata dagli uomini, diventasse un aspetto quasi negativo se declinato al femminile. Eppure, quando parliamo di Andrew Wiles, la sua determinazione viene celebrata, e la sua capacità di isolarsi dal resto del mondo per lavorare in autonomia alla dimostrazione non viene presa per presunzione, semmai gli viene riconosciuto il coraggio di aver rischiato tanto. Andrew Wiles ha avuto il coraggio di affrontare una sfida che aveva attraversato i secoli e, quando viene individuato un errore nella sua dimostrazione, prova a correggersi, impegnando altro tempo.

Non parla di presunzione, Gauss che, una volta conosciuta l’identità di Sophie Germain, le scrive:
«Il fascino di questa scienza sublime si rivela in tutta la sua bellezza solo a chi ha il coraggio di esplorarla. Una donna, a causa del suo sesso e dei nostri pregiudizi, incontra molti più ostacoli di un uomo nel familiarizzarsi con problemi complessi. Tuttavia, quando supera queste barriere e penetra nelle profondità più recondite, rivela di possedere il coraggio più nobile, un talento straordinario e un genio superiore.»
Per concludere, non può mancare un riferimento all’ultimo premio Abel, Michel Talagrand, che dichiara che «il segreto del successo in matematica è di lavorare ogni giorno fino a essere esausti ma non di più». Ne parlano, con dovizia di particolari, Beatrice Mautino ed Emanuele Menietti nel podcast del Post Ci vuole una scienza: Talagrand parla delle proprie difficoltà in matematica, legate a un “cervello lento” e a una “memoria terribile”, eppure dichiara di aver usato questo metodo proprio per superare le sue difficoltà. E direi che, visti i successi, non ci resta che fidarci!
Ricordo ora che anche Maryam Mirzakhani si è sempre definita una matematica lenta, ma è riuscita, nella sua breve vita, a raggiungere risultati eccezionali. Alex Eskin, dell’Università di Chicago, con il quale ha collaborato a lungo, racconta, nel film Secrets of the Surface, l’esperienza di lavoro con Maryam, paragonando il loro percorso a una camminata in montagna. Si trattava, come spesso succede, di una montagna inesplorata, e, a un certo punto, i due matematici hanno avuto l’impressione di poter raggiungere agevolmente la cima, quando un burrone ha sbarrato loro la strada. Con un sorriso dolce-amaro, Eskin racconta lo scoraggiamento che hanno provato, dato che quel burrone è costato loro due anni di duro lavoro e fatica. In tutto questo, Maryam si è mostrata positiva, anche se per un anno mezzo non ci fu nessun tipo di progresso. Per affrontare una fatica del genere e uscirne vittoriosi, è necessario avere una grande stabilità mentale e fiducia in sé stessi.
Aggiungendo queste caratteristiche alla caparbietà, credo proprio che il successo sia assicurato!
220 - 7 aprile 2024
La matematica è donna
Il profilo Instagram StorieScientifiche, la cui mission è, come scritto nella descrizione, il racconto della vita e delle scoperte «di uomini e donne che hanno contribuito, con le loro idee e i loro sogni, a portare avanti il progresso scientifico», il 24 marzo ha realizzato un post dedicato a Gigliola Staffilani, matematica presso il Massachusetts Institute of Technology, dove ricopre il ruolo di full professor (ovvero professore ordinario) in matematica pura, prima italiana di sempre e seconda donna della storia a ricoprire questo ruolo. La frase di apertura del post cattura l’attenzione: «Ho imparato, dopo molti anni, che dai fallimenti talvolta nascono grandi progressi». La sua storia ha dell’incredibile: famiglia contadina, orfana di padre a soli dieci anni, Gigliola sarebbe stata indirizzata dalla madre verso un futuro da parrucchiera, a causa della situazione complicata dal punto di vista economico che la sua famiglia stava vivendo. È solo per la sua bravura in matematica, per l’insistenza del fratello e per il sostegno dei professori che riuscirà a realizzarsi e ad avere un futuro nell’ambito della matematica. Tra gli aspetti interessanti della sua biografia che StorieScientifiche sceglie di mettere in evidenza, c’è il ruolo dell’insegnante del liceo scientifico Mario Illuminati, che le assegnava problemi difficili per i compiti a casa: «Io ero in grado di risolverli e mi rendeva estremamente felice».
Per un ulteriore approfondimento, si possono leggere le due interviste realizzate da Roberto Natalini per MaddMaths! La prima nel dicembre del 2010, e la piccola nota di redazione in apertura racconta parecchio di lei: si tratta di una segnalazione che i curatori dell’intervista hanno voluto fare dopo aver trascritto la registrazione, non solo perché è stato impossibile rendere l’accento abruzzese di Gigliola, che ora ha «qualche intrusione americana», ma anche perché «come si trascrive una risata?» Durante questa intervista, Natalini presenta la figura di Gigliola Staffilani a tutto tondo, facendola parlare delle sue scelte di vita, sia per lo studio che per la matematica, del ruolo delle donne, visto che è impegnata nella Association for Women in Mathematics (e fa notare che la situazione americana è peggiore di quella italiana), e fa infine un confronto tra il mondo della matematica americano e quello italiano. La seconda intervista, realizzata a luglio 2018, è apparsa originariamente sulla Newsletter della European Mathematical Society.
Matematica (da amare e) da insegnare
Alla domanda di Roberto Natalini: «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?», Gigliola Staffilani risponde: «metà e metà. Credo che l’intuizione arrivi quanto ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte». Altro aspetto interessante è che, dopo Illuminati, la Staffilani parla di un altro docente, il professor Sally, che le fece un assegno di 1500 $ per permetterle di restare in America: «Penso spesso a quel momento, una fortunata coincidenza, completamente casuale, che sarebbe potuta non succedere. Se così fosse stato la mia vita sarebbe stata completamente diversa!» Gigliola stessa è un’insegnante e dichiara che ha bisogno di sentirsi felice al lavoro, altrimenti sarebbe «una pessima ricercatrice, insegnante e mentore». Anche Federico Benuzzi parla di felicità per rispondere alla domanda di un ragazzo, al termine di un suo spettacolo: «Vorrei fare l’insegnante, me lo consiglia?» La risposta di Federico (e se avete avuto occasione di assistere a un suo spettacolo, potete confermarlo) è accurata e sottolinea come, per poter fare l’insegnante, siano necessari due amori: l’amore per la materia, che non è scontato, e l’amore per i ragazzi. L’amore per la disciplina è fondamentale, perché c’è bisogno di una passione per accendere la passione nei ragazzi e per poter trasmettere il sapere in maniera efficace (e non sempre è sufficiente, aggiungo io…), mentre l’amore per i ragazzi permette all’insegnante di riconoscere le loro potenzialità e di apprezzare quanto, a loro volta, i ragazzi insegnano. «Credo che siano questi gli ingredienti fondamentali per continuare a insegnare anni senza “colpo ferire”. Segreto per svegliarsi tutte le mattine alle 6.20 felice di andare al lavoro. Pietra filosofale per restare eternamente giovani!»
Matematica da comunicare
Pietro Minto, con il libro La seconda prova. Imparare la matematica, ci parla del suo secondo tentativo di affrontare lo studio della matematica, materia nella quale non aveva eccelso al liceo scientifico, per poter rifare la prova d’esame di matematica della maturità del 2006. Se avete dubbi in merito all’acquisto, leggere questo estratto pubblicato sul Post potrebbe aiutarvi a decidere: le pagine sono dedicate all’indagine sulla necessità (e utilità) delle incognite nell’algebra. Pietro Minto si concede anche la libertà di utilizzare formule semplici, guidandoci attraverso la storia della matematica.
Parlando di comunicazione della matematica, non si può non citare il quindicesimo anniversario di MaddMaths! (Auguri!). L’evento è stato ricordato sui social, condividendo l’articolo postato per il decimo anniversario. In effetti, quanto scritto da Roberto Natalini in quell’occasione è ancora attuale, richiamando «il dovere e la responsabilità di comunicare con il resto del mondo», visto che «la maggior parte dei non addetti ai lavori semplicemente ignora la ricerca matematica e la collega a sgradevoli ricordi scolastici». Nell’articolo si ricordano gli atti fondativi del sito, Roberto Natalini fa un po’ anche di mea culpa, ricordando i suoi precedenti, quando (forse) pensava «che chi si dedicava ad attività di comunicazione della matematica non avesse niente di meglio da fare». Dagli scarsi accessi dei primi tempi, dalle difficoltà nate dal fatto di essere dei pionieri, il sito MaddMaths! ha fatto parecchia strada, fino a diventare un punto di riferimento per i contenuti matematici che compaiono sulla rete.
Dialogando con la matematica
Giovedì 4 aprile si è svolta la terza diretta di quest’anno del canale IlariaF Math: l’ospite, Roberta Fulci, è una matematica, autrice di libri, redattrice e conduttrice di Radio3 Scienza, il quotidiano scientifico di Rai Radio 3. Nel corso della diretta, si è parlato di come Roberta Fulci sia approdata alla conduzione di questo programma, ideato da Rossella Panarese, un po’ per caso: appassionata di matematica, tanto da intraprendere il corso di laurea dopo il liceo classico, ha sempre pensato che si sarebbe dedicata alla ricerca, ma il suo senso di inadeguatezza l’ha spinta a scegliere di frequentare un master di comunicazione della scienza, per poter restare nell’ambito della matematica. Casualmente è arrivata alla redazione di Radio3 Scienza: obiettivo del programma che si trova a condurre è parlare di scienza rendendola accessibile a tutti e intrecciandola con altri aspetti della cultura e dell’educazione civica. Invitata dal pubblico, Roberta Fulci descrive il clima di collaborazione che caratterizza la preparazione di ogni puntata, che viene modificata fino all’ultimo minuto. Sempre su invito del pubblico, Roberta Fulci ha parlato anche delle sue emozioni una volta approdata alla facoltà di matematica, ricordando «il passaggio dalla sensazione di essere brava a quella di essere una rapa», visto che avere alle spalle il liceo classico non può che complicare le cose all’inizio dello studio universitario della matematica. Tra le puntate realizzate, Roberta Fulci parla in particolare della puntata dedicata alla matematica del colore, che ha avuto come ospite Edoardo Provenzi: la puntata non è più reperibile online, ma il professore ha realizzato una serie di articoli per MaddMaths! Interessante è la motivazione fornita per citare questa puntata: “Ho imparato tantissimo!” Nel corso della diretta, Roberta Fulci ha parlato anche delle sue opere: comincia con Ragazze con i numeri e Ragazze per l’ambiente, scritti insieme a Vicky De Marchi, per la collana Donne nella scienza di Editoriale Scienza e racconta di come, avendo scelto di dedicare una collana alle donne della scienza, le due sorelle che gestiscono la casa editrice si siano sentite dare delle kamikaze. E poi racconta del libro Il male detto, che parla del dolore fisico in termini matematici, visto che è un tentativo di darne una definizione. Vi invito a seguire con attenzione la diretta, visto che i racconti (che potete trovare anche nel libro) invogliano davvero alla lettura e la simpatia di Roberta Fulci è coinvolgente.
Festeggiando la matematica
Nei giorni scorsi, si è parlato ovunque di matematica, visto che il 20 marzo è stato assegnato il premio Abel. Come tanti altri, anche il premio Abel viene paragonato al premio Nobel, ma questo, effettivamente, è quello che si avvicina di più: pare sia nato proprio per dare ai matematici un premio equivalente al Nobel, viene assegnato ogni anno dal re di Norvegia e può contare su un premio equivalente a 700.000 euro. Quest’anno la scelta è caduta su Michel Talagrand per i suoi contributi innovativi nell’ambito della teoria della probabilità e dell’analisi funzionale. Dopo la prima presentazione realizzata da Stefano Pisani, MaddMaths! ha dedicato ampio spazio al premio, con un articolo di Adriano Barra, che racconta i risultati e i riferimenti, enfatizzati sui social, al premio Nobel di Parisi. Più di tutto, a me è piaciuta l’ultima puntata di Ci vuole una scienza, il podcast del Post curato da Beatrice Mautino ed Emanuele Menietti, perché non solo ne hanno parlato in modo entusiasta, ma hanno raccontato molto bene e con semplicità i risultati ottenuti. Sessantottenne, Michel Talagrand si è confrontato fin da piccolo con il dolore, dato che a causa di problemi di vista ha dovuto passare un lungo periodo in ospedale: studente mediocre prima della malattia, aiutato dal padre a superare le ore di buio ed isolamento a suon di matematica, ha imparato il potere dell’astrazione. A distanza di tanti anni, dice: «il segreto del successo in matematica è di lavorare ogni giorno fino a essere esausti ma non di più». Dichiara di lavorare in questo modo a causa delle sue difficoltà (!) in matematica, legate a un “cervello lento” e a una “memoria terribile”: lavorando molto e cercando di capire anche le cose più semplici, è riuscito a superare le proprie difficoltà e a vincere numerosi premi. Con tono di meraviglia, Menietti racconta del sito internet del matematico, che, per quanto semplice e vecchia maniera, risulta interessante e ricco di spunti. Personalmente, sono rimasta molto colpita dal rimpianto legato ad una sua scelta compiuta come insegnante, che ricorda ancora con amarezza dopo più di quarant’anni.
In chiusura, mi permetto un piccolo consiglio di lettura: lo spettacolo teatrale Il Signor Le Blanc di Maria Rosa Menzio pubblicato per Scienza Express. Continua il mio viaggio di approfondimento, mentre è ormai pronto lo script per il video con il quale parteciperò a #peopleformath2024!
Buona matematica e buon cammino! Ci sentiamo tra TRE settimane!
Daniela
Traduzione dell’immagine allegata: “Perché dovrebbero bannare il libro di Miss Sweet dalla biblioteca della scuola?” “Non ci posso credere… non posso proprio crederci!” “Forse ci sono alcune cose nel suo libro che non capiamo…” “In quel caso, dovrebbero bannare anche il mio libro di matematica!”
Il Signor Le Blanc
«Il Signor Le Blanc» è stato pubblicato da Scienza Express nel settembre del 2020: si tratta della trascrizione di uno spettacolo teatrale, che è stato rappresentato in prima assoluta a novembre del 2018. L’autrice è Maria Rosa Menzio, ex matematica, nota per la formulazione e dimostrazione del teorema di Menzio-Tulczjew in geometria simplettica, che ha fondato l’associazione culturale “Teatro e Scienza”, essendo diventata nel frattempo drammaturga e saggista. Maria Rosa Menzio dirige il Festival “Teatro e Scienza” che ha luogo in autunno a Torino dal 2007 (con la sola esclusione dell’edizione del 2012), e che nell’edizione del 2018 ha avuto come tema Matematica e altri demoni. Il testo dello spettacolo è preceduto dalla trascrizione di un intervento del professor Franco Pastrone, del Dipartimento di Matematica dell’Università di Torino, pubblicato in Conferenze e Seminari dell’Associazione Subalpina Mathesis. Nel suo intervento, Franco Pastrone formula giudizi abbastanza pesanti nei confronti di Sophie Germain, la matematica alla quale quest’opera è ispirata, parlando di «episodi rimasti famosi, forse un po’ forzati al fine di esaltare la determinazione della ragazza», e, pur riconoscendo che all’epoca una donna con un interesse intellettuale era vista come una «curiosità da salotto […] ma non su un piano di parità», la descrive come una persona dal «carattere non facile, spigoloso, con un fondo di presunzione che concorse a guastarle i rapporti con illustri matematici». Forse la scelta di certe sottolineature è il riflesso di un periodo meno dotato di sensibilità in merito al gender gap, visto che la conferenza risale al 1994-1995.
Il sottotitolo dell’opera teatrale è «Matematica e Resistenza nella Francia occupata dai Nazisti» e infatti Maria Rosa Menzio pensa proprio ad un connubio tra matematica e resistenza. I protagonisti della rappresentazione teatrale sono un narratore, testimone di quanto succede in Francia durante la Seconda guerra mondiale e testimone del dramma dei lager, una protagonista femminile, Marianne, che rappresenta la Francia occupata dai nazisti e, inizialmente indifferente a quanto sta succedendo, poi diventa un’eroina partigiana, il professor Levi, docente di matematica ebreo imprigionato dai nazisti e amante di Marianne, e Von Guderian, ufficiale nazista crudele, che seduce Marianne con l’inganno. La vicenda si svolge tra il 1943 e il 1944 e fin da subito scopriamo che il professor Levi e Von Guderian si conoscono da tempo: il nazista non ha mai perdonato al professore la bocciatura in matematica. Durante la prigionia il professore comincia a raccontare a Marianne, secondo quella che sembra essere una prassi consolidata, la vicenda di Sophie Germain, che assume l’identità del Signor Le Blanc per poter studiare matematica e che sarà una delle poche a riconoscere il genio di Evariste Galois. Sophie Germain è riuscita a crearsi un posto in un mondo prettamente maschile, anche se per molto tempo non le è stata riconosciuta la sua grandezza, come dimostrato dall’assenza del suo nome sulla Tour Eiffel, nonostante sia stata una pioniera nello studio dell’elasticità dei metalli.
Il racconto è piacevole, originale e coinvolgente: per quanto vedere lo spettacolo sarebbe stato meglio, la lettura permette di immaginare la rappresentazione teatrale. Le metafore aiutano lo spettatore / lettore a cogliere tutta la negatività del nazismo e la necessità dell’eroismo, per poter far trionfare la giustizia.
Nella quarta di copertina leggiamo: «Amore, tradimento e redenzione, fino allo scontro tra due carri armati e alla morte di Marianne (travestita da ufficiale nazista proprio col nome di Le Blanc) in un finale commovente e inaspettato».
Ellisse e iperbole aprile 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: geometria analitica, ellisse e iperbole
Durata: 120 minuti
Equazioni di secondo grado marzo 2024
Verifica di matematica, classe seconda liceo scientifico
Argomento: equazioni di secondo grado
Durata: 60 minuti
Ellisse e iperbole marzo 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: geometria analitica, ellisse e iperbole
Durata: 120 minuti





