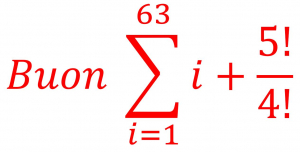Ci sono settimane particolarmente dense di matematica, in cui la newsletter pare scriversi da sola…

Matematica e Covid-19

Dopo aver tanto sentito parlare della pandemia, dopo aver seguito dirette e seminari, aver letto articoli e libri, ho deciso di fare un lavoro di sintesi di tutto il materiale raccolto per poterne parlare in classe, una quarta liceo scientifico, durante le ore dedicate all’educazione civica. Ho volutamente semplificato la parte matematica, perché i ragazzi potessero concentrarsi su alcuni aspetti per me fondamentali. Sul sito ho reso disponibili le slide, in formato pdf, che ho usato in classe e, per ogni puntata, ho fornito il link al video pubblicato su YouTube. È riportata inoltre la bibliografia di riferimento, composta da filmati e articoli.

Solo recentemente mi sono imbattuta nel filmato del canale MATH-segnale, Matematica delle epidemie, pubblicato a settembre. Nel filmato sono presenti delle simulazioni, che spiegano il funzionamento del modello SIR e delle app di tracciamento.

Siccome, in riferimento all’andamento dell’epidemia, si nomina spesso la crescita esponenziale e non è così facile coglierne la gravità, tanto che si parla, al riguardo, di un bias cognitivo (il link rimanda a un articolo del Corriere, che richiama un articolo della Bbc), può essere utile dedicare una manciata di minuti alla spiegazione di Veronica Grieco, studentessa di matematica all’Università di Genova e vincitrice di FameLab Italia 2019, che ci spiega come raggiungere la Luna con un foglio di carta.

Come ho già avuto occasione di dire, questa newsletter è nata, nel 2012, per condividere, con i miei alunni, link ad articoli e filmati che parlassero di matematica e per poter mostrare loro, non solo a parole, la presenza della matematica nella quotidianità. Tra quegli alunni c’era Marco Franzoni, che ha recentemente aperto un canale YouTube e sta dedicando alcuni dei suoi video proprio alla diffusione del Covid. In particolare, vi segnalo il filmato sul vaccino Pfizer-BioNTech: Marco ci racconta tutto quello che c’è da sapere, con competenza e precisione.

Matematica e attualità

In attesa del Festival di BergamoScienza che si svolgerà a ottobre, si prospettano alcuni incontri estremamente interessanti, con cadenza settimanale, che hanno luogo alle 18.30 del giovedì sul canale YouTube del Festival. Chi dovrebbe parlare di scienza in tv? è il titolo del primo incontro, che si è svolto ieri: il protagonista è stato Edoardo Boncinelli, noto biologo, genetista e Presidente Onorario del comitato scientifico del Festival, intervistato da Agnese Collino. La chiacchierata è stata davvero interessante e molte sarebbero le cose da evidenziare: la scienza è divertimento, ma va fatta seriamente e bisogna essere chiari, pur dovendo gestire la complessità di alcuni argomenti. Le indicazioni di Boncinelli, dedicate a chiunque voglia fare divulgazione, ma anche a chi “subisce” a volte alcuni interventi di presunti scienziati e dovrebbe sviluppare una propria competenza per poter scegliere, non tralasciano di ricordare che non dobbiamo cercare le certezze nella scienza e si concludono con un invito a studiare le scienze, «che sono belle». Dopotutto, la scienza è «la più bella avventura che possiamo vivere».

MaddMaths! ha annunciato ieri, 21 gennaio, la pubblicazione di un calendario della European Mathematical Society, con tutti gli eventi di divulgazione matematica, in Europa e nel Mondo. Si chiama Pop Math. «Il sito propone su una mappa interattiva tutti gli annunci di eventi di divulgazione della matematica per varie fasce di pubblico, e anche eventi professionali o accademici per coloro che lavorano nella divulgazione e comunicazione della matematica. Gli eventi censiti possono essere commerciali o gratuiti, online o di persona, e devono avere un inizio e una fine.»

Leggerezza e curiosità

Ieri sera mi sono divertita ad ascoltare l’intervista che Paolo Alessandrini (blog Mr Palomar) ha fatto ai Rudi Mathematici, ovvero Piotr R. Silverbrahms (Piero Fabbri), Rudy D’Alembert (Rodolfo Clerico) e Alice Riddle (Francesca Ortenzio). L’intervista è assolutamente da seguire, anche se non siete ancora abbonati alla loro rivista, che è online dal 1999.

Oggi pomeriggio, invece, ho seguito la conversazione con Sara Sesti, organizzata dalla Mathesis. Sara Sesti, autrice del libro Scienziate nel tempo, ha fatto una carrellata di donne della scienza, con la verve che la contraddistingue.

Continuano su MaddMaths! gli episodi di Matematica Danzante di Raffaella Mulas: il sesto episodio è dedicato a La regina degli scacchi: per spiegarci i meccanismi mentali che accomunano matematica e scacchi, Raffaella fa parlare Samuele Golfetto, matematico e scacchista. Nel settimo episodio si parla della bellezza della matematica con un esempio: la dimostrazione dell’infinità dei numeri primi. L’ultimo episodio pubblicato è dedicato ai nodi: per capire cosa c’entrino i nodi con la matematica, non vi resta che guardarlo.

Federico Benuzzi continua con le sue riflessioni sulla fisica, in questo caso sul gatto (delle nevi) di Schrödinger, il più famoso gatto della fisica. Essendo anche un giocoliere, sul suo blog ci parla della matematica dei giocolieri, Siteswap, «un potentissimo strumento che ha permesso non solo di descrivere, ma soprattutto di scoprire schemi che mai, altrimenti, si sarebbero potuti anche solo lontanamente immaginare.» L’esempio che ci fornisce è chiaro e illuminante.

Più leggero che mai è il filmato proposto sul canale YouTube di Roberto Esposito, Finalmente ho capito a cosa mi è servito studiare ingegneria aerospaziale. 3 minuti di pizza e matematica, su suggerimento di un ex alunno che studia ingegneria.

Consigli di lettura

Mi sono imbattuta nel libro di Pietro e Roberto Battiston, La matematica del virus, per preparare il mio lavoro sulla matematica delle epidemie. È un libretto veloce da leggere, ma fornisce un sacco di informazioni e, soprattutto, permette di esplorare i modelli SIR, dopo una piccola introduzione storica, a partire dal modello proposto da Bernoulli. È accessibile davvero a chiunque e permette di vedere con più chiarezza come venga studiato il diffondersi dell’epidemia: togliendo lo strato superficiale di ignoranza matematica, permette di essere più consapevoli delle misure di contenimento che vengono adottate e quindi di collaborare meglio con le autorità nella loro applicazione. Roberto Battiston, molto impegnato nell’ambito della divulgazione scientifica, non poteva perdere un’occasione come quella della pandemia per migliorare la nostra consapevolezza matematica.

Il secondo libro è stato scritto da Sofia Sabatti, che mi è capitato di incontrare nei miei anni all’università. Diario di bordo, pubblicato nella collana Righe e quadretti della casa editrice Mateinitaly, è un diario ma non è semplicemente un racconto, è un esempio di buona pratica didattica ma non è solo un testo di didattica. Con questo libro, Sofia Sabatti ci descrive l’insegnamento come una danza: ci sono passi avanti e passi indietro e, se questo può essere frustrante per l’insegnante, è anche vero che questa è la bellezza del percorso e non si riuscirebbe a realizzare coreografie tanto belle andando solo avanti.

Un piccolo posto nella mia newsletter lo merita Sara Kayali, 8 anni, siriana, che ha raggiunto un grande traguardo, «vincendo il primo premio al concorso Mondiale di matematica, organizzato dall’organizzazione cinese “ACIDA”. È stata in grado di ottenere il primo posto su 6.114 studenti e studentesse, partecipanti da 19 paesi di tutto il mondo.»

Buona matematica! Ci sentiamo tra TRE settimane!

Daniela

PS: Se volete sapere da dove arriva l’immagine allegata alla newsletter, ecco il link. L’ho vista in un post su Facebook di Sofia Sabatti e, visto quanto lei stessa ci dice sugli errori nel suo libro, non poteva esserci occasione migliore per condividerla.

«La matematica del virus», edito da Castelvecchi in ebook nel 2020, è stato scritto da Pietro Battiston, economista esperto di reti sociali dell’Università di Parma, e Roberto Battiston, ordinario di fisica sperimentale presso l’Università di Trento e direttore dell’Agenzia Spaziale Italiana dal 2014 al 2018.

Il testo è un piccolo saggio adatto a chiunque, che spiega come si può realizzare la descrizione della diffusione di un virus da un punto di vista matematico. Nell’introduzione, gli autori lasciano la parola a un virus che si racconta, come in un diario: gli umani sono, per i virus, «una gigantesca torta di cellule». Esattamente come il generale prussiano Karl von Clausewitz, citato all’inizio del secondo capitolo, il virus mette in atto tutta una serie di strategie per potersi diffondere velocemente e nel modo migliore possibile, ricorrendo ad alcune tattiche ingegnose: sceglie di non palesarsi in alcuni individui (gli asintomatici), in maniera tale da prendere il controllo della cellula senza che l’organismo se ne accorga e per poter diffondere meglio il contagio, e ha la capacità di effettuare delle mutazioni proprio per neutralizzare l’attacco del sistema immunitario. Nel terzo capitolo, dopo una breve introduzione storica da Bernoulli fino ai modelli compartimentali di Kermack e McKendrick del 1927, gli autori presentano i modelli che «hanno permesso la descrizione dell’evoluzione di molte epidemie, talvolta anticipandone gli esiti, e contribuendo individuare delle strategie di contenimento». Il modello SIR è sicuramente il modello compartimentale più semplice che possa essere applicato alla COVID-19 e, anche se forse non intuitivo, può spiegare adeguatamente come si diffonde un’epidemia.

Il quarto capitolo è introdotto dalla frase dello statistico George Edward Pelham Box: «Tutti i modelli sono sbagliati, ma alcuni sono utili». I due autori mostrano i pregi e i difetti del modello SIR che, in generale, è bello, utile e semplice, visto che considera gli esseri umani «come delle palline che rimbalzano in una scatola». Gli autori spiegano perché non è necessario considerare modelli più articolati, anche se le epidemie sono fenomeni complessi: il compito del modello è di aiutare a «capire la dinamica dell’epidemia, a partire dai dati raccolti durante il suo sviluppo.» Una volta identificato l’andamento dell’epidemia, permette di «anticipare gli esiti e valutare gli effetti degli interventi messi in atto per contenerla». Nel quinto capitolo, intitolato «Il diritto di contare bene», gli autori mettono in evidenza come per far funzionare adeguatamente un modello sia necessaria la massima apertura da parte delle istituzioni. Rendendo pubblici i dati, si può riuscire a caratterizzare l’epidemia nel modo migliore possibile, tanto più che nascondere i dati non aiuta a placare le critiche ma alimenta un clima di sospetto. «Il virus ha un grosso punto debole: se sul piano biologico è un oggetto efficientissimo e, almeno all’inizio, misterioso, sul piano della diffusione sociale si muove in modo piuttosto prevedibile a livello statistico. La matematica è quindi un suo nemico, mentre la cattiva raccolta dei dati è un suo alleato perché gli permette di mascherarsi.» Nella conclusione, gli autori mostrano come alcune informazioni fornite dai giornali non siano realmente significative e invitano ad affidarsi ai modelli compartimentali e ad un’analisi dei dati che cerchi il più possibile di avere una visione complessiva dell’evento.

«La matematica del virus» è accessibile davvero a chiunque e permette di vedere con più chiarezza come venga studiato il diffondersi dell’epidemia: togliendo lo strato superficiale di ignoranza matematica, permette di essere più consapevoli delle misure di contenimento che vengono adottate e quindi di collaborare meglio con le autorità nella loro applicazione. Roberto Battiston, molto impegnato nell’ambito della divulgazione scientifica, non poteva perdere un’occasione come quella della pandemia per migliorare la nostra consapevolezza matematica.

«Diario di bordo», terzo volume della collana Righe e quadretti della casa editrice Mateinitaly, è il primo libro di Sofia Sabatti ed è stato pubblicato a fine 2020. Insegnante alle scuole medie da circa vent’anni, Sofia Sabatti fa parte dello staff dei corsi MathUp, cura il sito Problemi per matematici in erba e il blog Matematomi e nel 2019 le è stato assegnato il Premio Cotoneschi, per la sua attività a favore della divulgazione della matematica, grazie all’entusiasmo che contraddistingue la sua azione educativa anche sul web e nei corsi di formazione per gli insegnanti.

Il libro è un diario ma non è semplicemente un racconto, è un esempio di buona pratica didattica ma non è solo un testo di didattica: «Diario di bordo» racchiude in sé entrambi questi aspetti e molto altro. Questo libro mostra che la scuola è un percorso di crescita non solo per gli alunni, come ci verrebbe naturale credere, ma anche per gli insegnanti che si pongono domande e sono in continua ricerca delle strategie migliori per poter portare i propri alunni alla comprensione. Inizialmente reticente all’idea di raccontare qualcosa di sé, Sofia Sabatti ci dice, al termine del libro, che «forse è una esperienza che vale la pena di essere raccontata» e, dopo averla seguita attraverso le pagine del suo libro, posso dire che è sicuramente un’esperienza che valeva la pena raccontare. Ci mostra le luci e le ombre del lavoro dell’insegnante e questa matematica, che può facilmente suscitare emozioni estreme nei nostri alunni, può far vivere tante emozioni anche agli insegnanti che provano a trasmetterne la passione: Sofia si deprime perché si sente inascoltata, si sente stanca, frustrata, piena di dubbi, prova un forte senso di colpa quando l’attività programmata si rivela un disastro, si arrabbia quando gli alunni cercano di evitare il lavoro, ma si ritrova anche a gongolare di fronte ad una bella risposta, prova stupore per certi ragionamenti svolti dai suoi alunni e si sente gli occhi luccicare dalla gioia. Viene colta ogni tanto dall’impazienza, dalla fretta causata dalla necessità di portare avanti il programma, dal nervoso per gli imprevisti che non le permettono di concludere un percorso, pur essendo pienamente consapevole che è importante ascoltare gli alunni invece di correggerli, per capire i loro percorsi e perché «forse dare l’occasione di sbagliare è la cosa migliore da fare, se si vuole che imparino qualcosa!». D’altra parte, anche l’insegnante deve lavorare su se stesso per non vivere l’errore solo come una pietra d’inciampo: per quanto ci provi, Sofia si accorge che non è possibile fare prevenzione all’errore, perché «dagli errori degli altri è molto raro che si impari qualcosa!»

Questo racconto non è una finzione narrativa: il diario rappresenta realmente ciò che Sofia fa e i suoi alunni sono, come tutti gli alunni, speciali, perché sanno vedere un’astronave in un poliedro particolare nel quale distinguono persino corridoi e stanze, ma al tempo stesso sono normalissimi ragazzini che, come Maxim, nel mezzo di un ragionamento chiedono di andare in bagno o di mangiare la pasta preparata dalla mamma durante la DaD.

«Diario di bordo» è una risorsa per ogni insegnante, perché non offre solo delle strategie e dei problemi da proporre, ma anche una riflessione didattica approfondita – grazie agli “Avvisi ai naviganti” di Maria Dedò, docente di Geometria presso l’Università degli Studi di Milano fino al 2014 – ma può essere una risorsa anche per gli studenti, che potrebbero trovare strategie per il processo risolutivo e riflessioni arricchenti. Non ci vengono descritte attività didattiche in modo astratto: sembra di sentire la voce di Sofia che ci racconta questo suo percorso e possiamo coglierne la frustrazione o la gioia nel momento in cui ce le racconta. Le attività che vengono presentate sono state fatte davvero, come dimostrano sia le foto nelle quali compaiono le mani degli alunni che hanno lavorato, sia le soluzioni offerte: si percepisce che le soluzioni proposte sono in realtà state rielaborate alla luce dei lavori fatti dai ragazzi.

Con questo libro, Sofia Sabatti ci descrive l’insegnamento come una danza: come nella danza ci sono passi avanti e passi indietro e, se questo può essere frustrante per l’insegnante, è anche vero che questa è la bellezza del percorso e non si riuscirebbe a realizzare coreografie tanto belle andando solo avanti. Dalle pagine della rivista Prisma, nel numero di gennaio di quest’anno, Sofia Sabatti non ci dice solo che il suo lavoro le piace: «Sento tutta la responsabilità di farlo al meglio che posso, per i ragazzi e le ragazze che ho vicini: sono loro il cuore pulsante del mondo di oggi e saranno loro le teste che dovranno prendere buone decisioni nel mondo di domani!»

Verifica di geometria, classe seconda liceo scientifico.
Argomento: circonferenza, poligoni inscritti e circoscritti.

Durata: 60 minuti.

Verifica di fisica, classe seconda liceo scientifico.
Argomento: cinematica unidimensionale.

Durata: 40 minuti.

Verifica di matematica, classe seconda liceo scientifico.
Argomento: radicali.

Durata: 60 minuti.

Dopo aver tanto sentito parlare della pandemia, dopo aver seguito dirette e seminari, aver letto articoli e libri, ho deciso di fare un lavoro di sintesi di tutto il materiale raccolto per poterne parlare in classe, una quarta liceo scientifico, durante le ore dedicate all'educazione civica. Ho volutamente semplificato la parte matematica, perché i ragazzi potessero concentrarsi su alcuni aspetti per me fondamentali:
- la soggettività dei modelli matematici scelti, perché, anche se ci piacerebbe molto, la matematica non ha tutte le risposte e a seconda del modello applicato potremmo avere una diversa previsione dell'andamento dell'epidemia;
- l'importanza dei media e delle notizie che diffondono: non bastano i numeri a garantire l'esattezza di una notizia. È importante scegliere con cura le proprie fonti e prediligere gli articoli scritti da esperti del settore;
- la necessità di accedere ai dati per poter fare una previsione adeguata;
- la validità delle precauzioni che ci sono state fornite: il distanziamento è fondamentale per limitare la propagazione del virus, anche se non ci piace.
In allegato sono disponibili le slide, in formato pdf, che ho usato in classe e, per ogni puntata, è fornito il link al video pubblicato su YouTube. Ad ogni puntata ho dedicato un'ora di lezione in classe, tranne che all'ultima: per la descrizione dei modelli SIR ho usato due ore di lezione.

PRIMA PUNTATA: Video
Introduzione storica: da Daniel Bernoulli a Ronald Ross, da Kermack e McKendrick a George MacDonald, il percorso che ha portato a studiare le epidemie dal punto di vista matematico, per prevederne l'andamento e ideare soluzioni.

SECONDA PUNTATA: Video
Il modello matematico: cos’è, come si applica, chi l’ha ideato. Vito Volterra e il suo discorso all’apertura dell’anno accademico all’Università di Roma nel 1901.

TERZA PUNTATA: Video
La matematica che leggiamo sui giornali: i numeri ci dicono tutto? Il bias cognitivo della crescita esponenziale: il nostro cervello non riesce a raffigurarsi una simile crescita e allora un semplice esempio può aiutarci a comprendere meglio il fenomeno. (La diretta di Paolo Alessandrini del 15 ottobre è stata la mia fonte di ispirazione principale: dopo aver visto il suo video, ho deciso di aggiungere questo passaggio a quelli che sarebbero stati, altrimenti, tre (e non 4) video sulla Matematica delle epidemie.)

QUARTA PUNTATA: Video
I modelli matematici usati per prevedere l’andamento delle epidemie. Descrizione in particolare del modello SIR, non usando le formule, ma partendo da un esempio numerico per arrivare al numero di soglia e al tasso Ro in modo da capire cosa possiamo fare in concreto per contribuire a limitare i danni.

BIBLIOGRAFIA E SITOGRAFIA:
Bell E. T., I grandi matematici, Saggi Sansoni, 2000
Colombo C., Diamanti M., Il vaccino contro il vaiolo: la querelle Bernoulli-d’Alembert e il calcolo della probabilità. Lettera matematica Pristem, n.91 Novembre 2014; 27-33
Guerraggio A., Il matematico che difese il vaccino. Prisma, n. 24 novembre 2020; 36-39
Quammen D., Spillover. Adelphi, 2017
MaddMaths!, Bulai I.M., I modelli matematici, strumenti potenti ai tempi della pandemia Covid-19 
MaddMaths!, Natalini R., Intervista con Andrea Crisanti: “Convivere con il virus grazie ai modelli matematici” 
MaddMaths!, Natalini R., I modelli matematici nell’era-covid? Hanno salvato milioni di vite umane 
De Tullio J., Che cos’è un modello matematico. Prisma, n. 22 settembre 2020, 22-23
Preziosi L., Modelli differenziali nelle scienze biomediche in Bartocci C., Odifreddi P. (a cura di), La matematica – Pensare il mondo (vol. IV). Einaudi, 761-793
Volterra V., Sui tentativi di applicazione delle matematiche alle scienze biologiche e sociali. Tipografia Fratelli Pallotta, Roma, 1902
Canale Paolo Alessandrini – Matematica: Matematica e Coronavirus, diretta del 15 ottobre 2020
Codogno M., Non prendete sempre alla lettera i numeri. Il Post, 10 ottobre 2020
Giordano P., Covid, contare i morti significa sentirli vicini. Corriere della Sera, 28 settembre 2020
Robson D., Exponential growth bias: The numerical error behind Covid-19. BBC, 13 agosto 2020
Saporiti R., Il Covid-19 e la seconda ondata (di infodemia): diffidate di chi usa i numeri assoluti. Il Sole 24 Ore, 6 ottobre 2020
Le tabelle con i dati distinte nazione per nazione 
Le tabelle e i file csv forniti da Il Sole 24 Ore 
I dati della Lombardia di Stefano Martire
Beutelspacher A., Le meraviglie della matematica. Ponte alle grazie, Milano 2008, cap. 6, 23-26
Autiero M., Educazione civica e matematica, esempi di best practices al Liceo Classico J. Sannazaro, diretta YouTube del 17 novembre 2020
Battiston R., Modelli compartimentali e interpretazione dei dati dell'epidemia COVID19 in Italia, diretta YouTube del 15 dicembre 2020
Alessandrini P., La matematica delle epidemie (parte prima), blog Mr. Palomar, 26 febbraio 2020
Alessandrini P., La matematica delle epidemie (parte seconda), blog Mr. Palomar, 28 febbraio 2020
Battiston P., Battiston R., La matematica del virus. I numeri per capire e sconfiggere la pandemia. Castelvecchi, 2020

DaD e aggiornamento

La Mathesis Nazionale ha proposto recentemente tre incontri culturali: il primo è stato una conversazione con Chiara Valerio, l’autrice di La matematica è politica, e si è svolto il 28 dicembre, mentre il secondo era una conversazione con la famosa Gabriella Greison e si è svolto il 29 dicembre (del terzo incontro, che si svolgerà con Sara Sesti il 22 gennaio, parleremo la prossima volta). Le chiacchierate sono state interessanti e stimolanti: Chiara Valerio ha approfittato dell’occasione per parlarci della comunità dei matematici, ribadendo che nessuno lavora realmente da solo e ha ricordato che la difficoltà della matematica sta nel suo linguaggio, così diverso da quello che usiamo abitualmente. Ma ne vale la pena! Acquisendo un po’ di confidenza con la matematica ovvero continuando a frequentarla, avremo un metodo di interpretazione del mondo che annulla le distanze nello spazio e nel tempo. Altrettanto interessante e stimolante è stato l’incontro con Gabriella Greison, che ha fatto della sua passione per la fisica del Novecento il suo lavoro e che riesce a parlare di concetti difficili anche al grande pubblico.

È stato estremamente istruttivo e interessante seguire la conferenza del prof. Roberto Battiston, ordinario di fisica sperimentale presso l’Università di Trento, che, sempre per la Mathesis Nazionale, ha parlato dei modelli compartimentali, interpretando i dati dell’epidemia Covid-19 in Italia. I grafici aiutano tantissimo a comprendere gli studi di Battiston, anche se le equazioni che rendono possibile la previsione del contagio sono equazioni differenziali: la sua parlata sciolta è coinvolgente e non annoia.

Matematica e attualità

La voce emozionata di Rossella Panarese ha guidato la puntata di Radio3Scienza del 21 dicembre, dedicata a Pietro Greco, giornalista scientifico e conduttore di Radio3Scienza, scomparso improvvisamente il 18 dicembre scorso. Il primo ospite è Telmo Pievani, professore ordinario presso il Dipartimento di Biologia dell’Università degli Studi di Padova. Questa puntata è una serie di «ricordi di esponenti del giornalismo scientifico come Cristiana Pulcinelli, Fabio Pagan, Eva Benelli e Silvia Bencivelli; e poi i ricordi della squadra di Radio3Scienza: Marco Motta, Elisabetta Tola, Roberta Fulci, Francesca Buoninconti, Paolo Conte», ma anche di spezzoni di puntate della trasmissione condotta da Greco.

Leggerezza e curiosità

Quanti litri di acqua servono per riempire una vasca da bagno? Forse non ci avete mai pensato: prova a farci riflettere Federico Benuzzi, proponendoci i problemi di stima, che sono noti anche come problemi di Fermi. Fermi aveva infatti l’abitudine di proporre problemi di questo tipo ai suoi studenti, come quando chiese: “Quanti accordatori di pianoforte ci sono a Chicago?”. Federico Benuzzi ci dimostra che la matematica è uno strumento indispensabile per non farci prendere in giro, per imparare a gestire i grandi numeri e per capire la realtà che ci circonda. Il video successivo è il cavallo di battaglia di Benuzzi: le videoslot dei bar, ovvero il gioco d’azzardo, e scoprirete così cosa abbia a che fare il cane di Pavlov con le videoslot.

Continuiamo a seguire le puntate della Matematica Danzante su MaddMaths! Raffaella Mulas riesce a rendere curiosa e simpatica anche la topologia (che, lo confesso, non ho amato molto durante il mio percorso universitario), usando la plastilina e la sfera selvaggia di Alexander. L’episodio 3 invece, rigorosamente di un minuto, ha a che fare con la teoria del caos ed è proprio una matematica danzante, perché in questo caso Raffaella riesce, pur muovendosi a caso, ad avere un certo ordine e, quindi, a sembrare una matematica che danza. La quarta puntata è dedicata a Newton: non poteva essere altrimenti, trattandosi della puntata natalizia. La quinta puntata è un invito al risparmio: tenete da parte il calendario o l’agenda del 2020, se non l’avete usata, perché potrebbe tornarvi utile del 2048.

Paolo Alessandrini festeggia oggi i 10 anni del suo blog, Mr. Palomar. Divulgatore e insegnante di matematica, Paolo ha pensato a due iniziative per celebrare l’evento: su Facebook rilancerà alcuni dei post più significativi che sono stati maggiormente apprezzati nel corso dei dieci anni, ma usando l'hashtag #augurimrpalomar ognuno di noi ha la possibilità di scrivere qualcosa a Paolo, fino a metà gennaio. Chi parteciperà avrà l’occasione di ricevere dall’autore un pdf esclusivo.

Il 7 dicembre scorso, Roberto Natalini, Direttore dell’Istituto per le Applicazioni del Calcolo “M. Picone” del CNR, ha riportato, in un post su Facebook, l’esito di un sondaggio svolto su Twitter, nel quale interrogava i suoi follower in merito alla parità dello zero. Il 19 dicembre, il canale YouTube MATH-segnale ne ha fatto un video intitolato, per l’appunto, parità dello zero. La domanda non sembrerebbe essere legata a un problema reale, eppure durante il video ci viene presentato un problema reale alla base di questa domanda.

Forse non avete mai sentito nominare il fisico russo Igor Tamm, ma questo episodio della sua vita vi mostrerà come la matematica possa realmente salvare la vita: vale la pena leggerlo!

Matematica e... poesia: questo video di Francesco Malaspina, autore di Sette semplici lezioni di matematica, ci parla della poesia della matematica e si conclude con un simpatico sonetto, che parla sia dell’amore per la matematica (e della matematica), sia dell’utilità della stessa.

Consigli di lettura

Dopo aver scoperto l’abilità di Marie Benedict con La diva geniale, non ho potuto che leggere La donna di Einstein: la triste storia di Mileva Marić, l’altra Einstein, come l’ha indicata il titolo originale del romanzo. Il libro è un romanzo piacevole, raccontato in prima persona da Mileva. Le emozioni che la donna ci permette di vivere attraverso il suo racconto sono intense, tant’è che ho faticato ad arrivare all’ultima pagina del romanzo sapendo fin dall’inizio quale sarebbe stato il triste epilogo di questa storia, sapendo cioè che Mileva, dopo essere vissuta all’ombra del marito durante il loro matrimonio, sarebbe tornata nell’ombra di una vita anonima al momento del loro divorzio.

Per chi ama i fumetti e potrebbe apprezzare una visione umoristica della ricerca scientifica, Dipartimento di Teorie folgoranti, scritto da Tom Gauld, è la scelta giusta: leggendo questo libro mi sono ritrovata non solo a ridere spesso, ma anche a fotografare numerose pagine per poi inviarle ai miei contatti. Si mostra perfettamente all’altezza l’introduzione di Francesco Guglieri, editor di Einaudi, che presenta il libro usando una storia a bivi.

Tra i consigli di lettura non può mancare, tra i buoni propositi per l’anno nuovo, la scelta di un abbonamento a Prisma, unica rivista italiana di divulgazione matematica: ci parla dei modelli che studiano la diffusione del Covid-19, ad esempio, del gioco d’azzardo, ma propone anche giochi matematici, capaci di appassionare i lettori di tutte le età.

Tra i suggerimenti di lettura, può rientrare anche la rassegna dei 10 post più letti su MaddMaths! nel 2020: il Covid la fa da padrone, ma c’è anche molto altro.

Concludo questa newsletter con un oroscopo, ma non è un oroscopo qualsiasi: è l’oroscopo matematico, proposto da MaddMaths! Paul Erdős, Maryam Mirzakhani, Margherita Hack, Alan Turing, Pierre de Fermat, Bernhard Riemann, Evangelista Torricelli, Évariste Galois, Werner Karl Heisenberg, lo sconosciuto Ludvig Lorenz, David Hilbert e Georg Ferdinand Ludwig Philipp Cantor ne sono i protagonisti: leggete l’oroscopo per scoprire quale grande nome ha a che fare con voi.

Buona matematica! Ci sentiamo tra TRE settimane!

Daniela

«Dipartimento di teorie folgoranti», edito da Mondadori nel 2020, è stato scritto da Tom Gauld, fumettista scozzese che collabora regolarmente con il Guardian, il New Yorker e il New Scientist. In particolare, questi fumetti sono apparsi originariamente proprio sul New Scientist.

Le vignette sono precedute da un’introduzione di Francesco Guglieri, editor di Einaudi, che collabora con il quotidiano “Domani” e con il mensile “Il” del Sole24ore e ha scritto articoli, racconti e reportage su vari giornali e riviste. L’introduzione, definita dallo stesso autore “folgorante”, è una storia a bivi (tipologia nata proprio nel mondo dei fumetti) che di fatto è come un viaggio tra le varie dimensioni della scienza. Guglieri ci racconta che, come Coleridge seguiva le lezioni di chimica della Royal Institution «per arricchire la sua riserva di metafore», Tom Gauld «con gli strumenti dell’ironia e della genialità grafica ha capito una cosa: che la scienza, con le sue scoperte, i mondi che ci dischiude… con i suoi giochi, anche… può essere uno straordinario deposito di bellezza». È proprio per questo motivo che «gli scienziati non sono secondi ai più visionari tra i poeti». E questa è l’impressione che si ha navigando fra queste 150 vignette che spaziano nel mondo scientifico, prendendo in giro alcune manie degli scienziati, ma mostrandoci anche i lati più nascosti della ricerca, protagonista in questo percorso. Gauld ci mostra cosa succede quando la ricerca va male, ma poi c’è spazio per la meccanica quantistica, il gatto di Schrödinger, il cane di Pavlov e la diffusione dei virus, c’è un generatore di titoli per libri divulgativi di successo, c’è spazio per la storia della scienza con Newton e Archimede, ad esempio, ci sono situazioni paradossali, c’è il confronto con la vita reale e la reinterpretazione della vita reale, ci sono gli appunti per lo scienziato pazzo in una conferenza stampa, ma c’è anche un vignetta nella quale vengono mostrati i vari stati della materia e che potrebbe essere usata con fini didattici… insomma c’è un po’ di tutto!

Leggendo questo libro mi sono ritrovata non solo a ridere spesso, ma anche a fotografare numerose pagine per poi inviarle ai miei contatti e per ognuno di loro e a seconda di quello che era il loro ruolo nell’ambito della ricerca scientifica, poteva esserci qualcosa di interessante all’interno di questo libro. Insomma, io già adoro i fumetti ma questo «Dipartimento di teorie folgoranti» offre uno spaccato della ricerca scientifica davvero entusiasmante e credo che non perderò occasione per utilizzare queste vignette nel presentare gli argomenti più complessi in classe. Grazie a Tom Gauld per questo momento di svago, ma al tempo stesso di approfondimento perché, come dice Guglieri nell’introduzione, «riesce a mettere in comunicazione la pancia con la testa».

«La donna di Einstein», pubblicato da Piemme nel 2017, è stato scritto da Marie Benedict, che ha lavorato in passato come avvocato a New York, ma la cui passione per la storia è stata lo stimolo per dedicarsi a romanzi storici come quello in questione. È la stessa autrice a dirci che non conosceva molto Einstein e di fatto non sapeva nulla della prima moglie Mileva Marić: l’ha conosciuta quando si è ritrovata ad aiutare il figlio Jack a preparare una relazione sul libro per bambini Who was Albert Einstein, e il fatto che si accennasse solo di sfuggita alla prima moglie, a sua volta una studiosa di fisica, l’ha incuriosita. È così quindi che nacque questo romanzo: è l’autrice stessa nella nota finale, nella quale elenca anche la bibliografia che l’ha aiutata nella stesura, a sottolinearci quali siano gli aspetti puramente inventati della vicenda e quali invece realmente accaduti. «Ogni qual volta mi è stato possibile, nell’arco generale della storia (date, luoghi, nomi) ho cercato di attenermi ai fatti, prendendomi libertà necessarie ai fini narrativi». Ci ricorda inoltre che scopo del libro non è quello di «sminuire i contributi dati da Albert al genere umano e alla scienza ma far conoscere l’umanità delle persone dietro quei contributi scientifici. La donna di Einstein si propone di narrare la storia di una donna brillante la cui luce è andata perduta nella gigantesca ombra gettata da Albert: quella di Mileva Marić.»
Marie Benedict immagina che Mileva, l’altra Einstein – come suggerisce il titolo originale del libro –, ripercorra la propria vita alla ricerca di una risposta: «Come ho fatto a smarrire la strada?»

Il romanzo ha inizio il 20 ottobre del 1896 a Zurigo, la prima volta che Mileva mette piede al Politecnico: è proprio durante una lezione del professor Heinrich Martin Weber che incontra Albert Einstein, che attira subito la sua attenzione con la sua «zazzera scarmigliata di riccioli scuri», visto che non le levava gli occhi di dosso. Il libro si conclude il 29 luglio del 1914 a Berlino, il giorno in cui, dopo aver preso accordi per il divorzio, Mileva rientra con i figli a Zurigo. Al termine di tutto c’è l’epilogo del 4 agosto del 1948, il giorno della morte di Mileva, nel quale essa dà una spiegazione delle tre parti in cui è stato suddiviso il libro: quasi come in un tributo a Newton e alla fisica, le tre parti sono scandite dai tre principi della dinamica dato che, ci dice Mileva, «da fanciulla pensavo che il principio si applicasse unicamente ai corpi inanimati; soltanto più tardi ho compreso che anche le persone agiscono in sua conformità.»

Prima dell’arrivo a Zurigo la vita di Mileva «ha continuato a snodarsi in linea retta finché non è intervenuta una forza esterna. Albert è stato quella forza». La seconda parte, con il secondo principio della dinamica, inizia il 12 Aprile del 1898 e si chiude il 14 Marzo 1913: inizia con il ritorno di Mileva a Zurigo, dopo la frequenza di un semestre a Heidelberg in Germania, e si chiude nel momento in cui Mileva cambia di nuovo la sua traiettoria. «La forza Albert ha agito su di me in conformità con la seconda legge del moto. Sono stata risucchiata nella sua direzione e nella sua velocità, e la sua forza è diventata la mia». Nella terza parte, con il terzo principio della dinamica, Mileva, non riuscendo più a reggere la forza di Albert, ha «esercitato una forza uguale in grandezza e contraria in direzione rispetto alla sua», ovvero rispetto a quella di Einstein. Ed è così quindi che si conclude questa storia d’amore.

Nelle sue ricerche, Marie Benedict ha scoperto che Mileva è diventata «il punto focale di un dibattito assai vivace nel mondo della fisica. La discussione, che verteva intorno alla parte da lei avuta nella formulazione delle pionieristiche teorie del marito del 1905, era divampata ancora di più in seguito al ritrovamento, negli anni Ottanta, del carteggio intercorso tra i due dal 1897 al 1903.» È abbastanza evidente che Mileva abbia avuto un ruolo nelle scoperte di Einstein e nell’annus mirabilis, il 1905, durante il quale furono pubblicati i quattro articoli sugli Annalen der Physik. Quale sia stato questo ruolo però non è dato sapere: sono molti i dubbi attorno alla loro storia: non si sa se Mileva sia stata semplicemente una «cassa di risonanza per le idee di Albert» oppure se l’abbia aiutato solo con la matematica oppure ancora se il suo ruolo sia stato di gran lunga più cruciale. L’autrice sposa proprio quest’ultima ipotesi.

Il libro è un romanzo piacevole, raccontato in prima persona da Mileva. Le emozioni che la donna ci permette di vivere attraverso il suo racconto sono intense, tant’è che ho faticato ad arrivare all’ultima pagina del romanzo sapendo fin dall’inizio quale sarebbe stato il triste epilogo di questa storia, sapendo cioè che Mileva, dopo essere vissuta all’ombra del marito durante il loro matrimonio, sarebbe tornata poi nell’ombra di una vita anonima al momento del loro divorzio. «Ho assistito alla canonizzazione di Albert come santo laico. Ciò nonostante, mai una volta ho provato il desiderio di tornare al ruolo di sua moglie. Tutto ciò a cui sempre avrei voluto tornare è il ruolo di madre di Lieserl.»