Visualizza articoli per tag: curiosità
Matematica in campo
«Matematica in campo» è stato pubblicato nel 2023 dalla Casa Editrice Hoepli, nella collana Telescopi. L’autore è Paolo Alessandrini, che, sempre per Hoepli, ha scritto anche Matematica Rock e Bestiario matematico, finalista al Premio Asimov 2022. «Matematica in campo» è entrato nella classifica Book Award 2023 di TuttoSport, ottenendo il terzo posto, ed è stato dichiarato il miglior libro di calcio del 2023.
Paolo Alessandrini riesce a coniugare le sue due passioni, il calcio e la matematica: fin da piccolo, il calcio ha rappresentato per lui libertà e felicità e, avendo notato molti punti di contatto con la matematica, ha scelto di fare questa originale presentazione. Obiettivo del libro è quello di rispondere alla domanda se il calcio sia una scienza o un’arte o, meglio, come specifica nell’introduzione: «un freddo calcolo o una storia d’amore». Effettivamente, se parliamo di scienza, e di matematica in particolare, ci sembra di cogliere una certa freddezza in queste discipline, forse collegata agli algoritmi e alla loro prevedibilità, mentre all’arte associamo un’idea di imprevedibilità, che richiama il mondo delle emozioni. Fin dall’inizio, Paolo Alessandrini invita a riflettere sul fatto che «forse il segreto del successo [del calcio] sta proprio in questa sua duplice essenza».
Il testo è strutturato come una partita immaginaria e il pre-partita coincide con l’organizzazione del tornei, strutturati in gironi all’italiana, a eliminazione o misti: Alessandrini li presenta con diagrammi ed esempi, per mostrare la scelta migliore in funzione dell’obiettivo, usando il calcolo combinatorio e i diagrammi ad albero. Il primo tempo si suddivide in due capitoli, entrambi dedicati alla geometria: si comincia con un grande classico, il pallone, che non è propriamente una sfera, ma è stato a lungo un icosaedro troncato, ovvero un’approssimazione (ben riuscita!) di una sfera. Con sistematicità e ricchezza di particolari, Alessandrini traccia la storia del pallone e delle sue forme, dal teorema di Pogorelov ai solidi platonici ed archimedei, mostrando come tutto tenda a una soluzione ottimale, in equilibrio tra una traiettoria affidabile e un basso numero di cuciture. Il secondo capitolo è dedicato agli errori arbitrali, nei quali spicca come la geometria debba scendere a patti con la fallacia dell’occhio umano, spesso vittima di illusioni ottiche.
L’intervallo è dedicato al calcolo delle probabilità, strumento per indagare la prevedibilità del gioco. Anche in questo caso, lo spettacolo del calcio sfrutta l’equilibrio tra la bravura dei giocatori e il caso: «il calcio è fatto di tanti piccoli episodi, molto spesso imprevedibili e incomprensibili se considerati da vicino. Ma se li osserviamo con una lente grandangolare, li inseriamo in un contesto più ampio e li analizziamo con strumenti matematici evoluti, acquistano un significato e lasciano emergere una struttura logica.»
Nel secondo tempo, diventa fondamentale l’analisi dei dati (come le statistiche che compaiono sullo schermo durante le partite), che ha preso piede a partire dagli errori di Charles Reep, ed è diventata ciò che conosciamo oggi con Valerij Lobanovs’kyj e lo statistico Anatolij Zelentsov. Per quanto l’applicazione della matematica dia l’idea, nell’immaginario collettivo, di un calcio prevedibile e arido, Alessandrini fa notare che «le vere squadre non giocano a caso, ma adottano scelte tattiche più o meno complesse, e lo fanno soprattutto perché è più vantaggioso». Mentre la storia del calcio resta sullo sfondo e permette di capire più a fondo il regolamento del gioco, gli schemi del secondo capitolo fanno intravedere l’applicazione dei modelli matematici e l’impiego dei grafi per lo studio delle reti di passaggi, che aiutano a tracciare le caratteristiche della squadra: l’indice di centralità ci dice come il calcio sia realmente uno sport di squadra, e l’indice di coesione può misurare l’affiatamento tra i giocatori.
La fisica interviene nei tempi supplementari, con il classico moto parabolico e la fluidodinamica, ma è la matematica con la curva perfetta, l’iperbole, che aiuta a individuare la zona migliore per calciare un tiro in rete. Negli ultimi due capitoli, dedicati ai calci di rigore e al post-partita, la protagonista è la teoria dei giochi: attaccante e portiere sono impegnati in un gioco di strategia, nel tentativo di prevedere le mosse dell’avversario, mentre i punteggi assegnati all’esito della partita possono essere studiati nelle loro sfumature grazie alla matematica, che può anche aiutare a valutare il rischio di accordi pre-partita.
Nella sua conclusione, Paolo Alessandrini dà finalmente una risposta alla domanda che ha percorso le pagine del libro, chiedendo, a sé stesso e al lettore, «perché dovremmo avere paura di qualcosa che può aiutarci a comprendere meglio la realtà?». La matematica costituisce uno strumento in più: «la bellezza, se è vera bellezza, è eterna e indistruttibile: l’approccio razionale non ambisce a profanarla, ma soltanto a contemplarla in modi nuovi» e forse il calcio può aiutare a renderci più consapevoli della creatività insita nella matematica.
L’aspetto leggero del testo è enfatizzato dalle citazioni di Vujadin Boskov, l’allenatore più nominato, perché le sue perle di saggezza offrono sempre l’occasione per una risata: «Pallone entra quando Dio vuole»! Numerosi esempi, che ci fanno sentire l’emozione dello sport, costellano la narrazione, mentre la struttura articolata e curata mette in evidenza il rigore matematico, facendo cogliere al lettore lo studio approfondito che resta sullo sfondo, enfatizzato anche dalle immagini, in gran parte realizzate dall’autore, che offrono un supporto a quanto già spiegato nel dettaglio e con semplicità. Se è vero che il calciatore non si affida alla matematica e alla fisica, quanto all’esperienza, all’istinto e alle capacità tecniche, è fuor di dubbio che «la matematica e la fisica offrono strumenti formidabili per comprendere le situazioni che si verificano sul terreno di gioco, ma non dobbiamo dimenticare che esse costituiscono soltanto uno dei possibili punti di vista: in alcuni casi rappresentano una prospettiva privilegiata e preziosa, in altri sono destinate a fornire indicazioni troppo imprecise».
Saltando da un pensiero all'altro
2 gennaio 2024: dopo essere stato fermo un turno a dicembre, il gruppo del Carnevale della Matematica viene richiamato all’ordine. Flavio Ubaldini invita i partecipanti a produrre i propri contributi, offrendo come tema la matematica bisestile.
Mumble mumble…
A me viene in mente solo “anno bisesto, anno funesto”, ma sulla stessa linea trovo “anno bisesto che passi presto”, “anno bisestile chi piange e chi stride”, ma credo che, pur parlando di matematica, Flavio non avesse in mente le lacrime quando ha proposto il tema.
Mumble mumble…
Che significa matematica bisestile? Secondo il dizionario Treccani bisestile deriva dal latino bisextus, che significa “due volte sesto”, «secondo l’uso romano di contare due volte, negli anni bisestili, il 6° giorno prima delle calende di marzo (giorno bisesto), cioè il 24 febbraio». Ma quindi devo parlare di una matematica che si ripete? Se digito “matematica che si ripete” in Google, trovo: frattali, «figura geometrica che si ripete all’infinito uguale a sé stessa, su scala sempre più piccola». Sì, i frattali sono nel mio cuore da quando con la mia scuola abbiamo partecipato all’edizione del 2018 di BergamoScienza, ma… non credo sia questa la matematica bisestile.
Mumble mumble…
Digito “matematica bisestile” in Google e mi ritrovo con una serie di link per aiutarmi a capire cos’è un anno bisestile, ma non molto in merito alla matematica. Forse se cercassi in inglese… Ma come si dice “anno bisestile” in inglese? Leap year. Ma cosa significa leap? Salto! In realtà, cercando “leap year in math” trovo un paio di link interessanti: il primo è il blog Slate (che significa lavagna) dell’astronomo, divulgatore scientifico e blogger Philip Plait, Leap days explained!, e il secondo è una spiegazione matematica del sito della NASA, Leap day math. L’immagine scelta da Phil Plait in apertura di articolo è quella di una simpatica capra che salta, mentre il link della NASA porta a un breve pdf schematico ed esaustivo. Potrebbe essere sufficiente, ma…
Mumble mumble…
9 gennaio 2024: faccio un salto in libreria. Aggirarsi tra gli scaffali è, per me, rilassante e fonte di ispirazione, anche se, purtroppo o per fortuna, trovo sempre qualcosa da comprare. Non abito in una grande città e le librerie della zona sono abbastanza piccole e poco fornite per quando riguarda la parte matematico-scientifica. Se voglio avere qualche possibilità di successo, devo esplorare gli scaffali dedicati ai bambini: per i più piccoli, si trova parecchio in termine di divulgazione scientifica. Sembra che gli adulti abbiano sempre molto da spiegare ai bambini, forse perché sono ancora alla scoperta del mondo, forse perché questi sono più curiosi rispetto agli adulti. Con la scusa di regalarli ai nipoti, ho comprato un paio di testi che mi hanno ispirato. Il primo è L’atlante del tempo, di Tommaso Maiorelli, con le illustrazioni di Carla Manea: «il tempo è un’acqua profonda e misteriosa, e la Storia è lo scorrere impetuoso di quest’acqua. E allora la Storia è un fiume, con tutto quello che ci sta dentro» e gli uomini nuotano e navigano su questo fiume. In uno dei primi capitoli scopriamo che la linea del tempo non è sempre stata una linea e, mostrandoci «La linea del tempo del tempo», Maiorelli ci illustra la GEOMETRIA del tempo! Per i Babilonesi, il tempo era un ciclo senza fine, un CERCHIO, quindi, per il buddhismo, il tempo affronta «infiniti cicli eterni», per la tradizione greca e quella romana il tempo è come «una SFERA che abbraccia tutto». Maya e Aztechi elaborarono un calendario complicato, ma sostanzialmente «composto da moltissimi cicli e sotto cicli». D’altra parte, ciò che osserviamo attorno a noi ci rimanda all’idea del ciclo: «Primavera, estate, autunno, inverno e poi ancora primavera… Gli alberi nascono dai semi, crescono e prima di morire danno frutti che a loro volta daranno altri semi». È il cristianesimo a spezzare il cerchio e a cominciare a pensare al tempo come a una LINEA, una linea con un verso di percorrenza preferenziale, secondo quanto confermato dalla termodinamica. Eppure, i grandi filosofi non ci fanno mancare, nel corso dei secoli, ulteriori immagini geometriche: per Henry Bergson, «Il tempo vissuto […] è una “PALLA di neve” che ruzzolando si ingigantisce sempre di più», mentre per Hegel «la Storia avanza e si sviluppa progressivamente e il tempo “cresce” all’infinito su sé stesso, come in un vorticoso movimento a SPIRALE».
Non è solo la rappresentazione del tempo ad essere geometrica, perché anche per misurare il tempo l’uomo cerca il supporto della matematica: CERCHI di pietre celebri come quello di Stonehenge in Inghilterra non sono altro che «pesanti calendari di pietra», mentre le prime clessidre ad acqua, inventate dagli Egizi, sono costruite con vasi CONICI con un piccolo foro alla base.
La misura del tempo si affina con il tempo (!) e le unità di misura si evolvono con essa, come riportato ampiamente nel libro Quanti? Tanti! di Sandra Lucente, che esplora la matematica, la fisica, l’archeologia, la letteratura, … tutto ciò che ruota attorno alla misura e agli ordini di grandezza.
Le misure del mondo di Andrea Minoglio con le illustrazioni di Bethany Lord è il secondo acquisto: in questo libro, che permette di esercitare anche l’arte della stima, fornendo il confronto tra elementi naturali e costruzioni, ci parla del tempo usando le PROPORZIONI, visto che ci imbattiamo nella storia della Terra in 12 ore. Il riferimento al calendario cosmico ideato dall’astronomo e divulgatore statunitense Carl Sagan è evidente: «il calendario è formato da un unico anno terrestre, ma in questo arco temporale viene compressa la cronologia dell’intero universo». Se volete risparmiare tempo (!), un breve short di Erik Viotti, (conosciuto sui social come il Prof di Montagna) che usa il calendario cosmico per fare i suoi auguri a inizio anno, vi dirà tutto ciò che serve. Siccome per i più piccoli anche un anno è difficile da visualizzare (il senso del tempo cambia crescendo, dilatandosi con l’età), un intervallo di 12 ore, dalle 8:00 alle 20:00, rende meglio l’idea: la vita ha origine solo alle 9:25, ma esplode alle 18:34, i continenti si formano alle 19:31 e solo alle 19:50 si diffondono i mammiferi, e mentre i primi arnesi in pietra fanno la loro comparsa alle 19:59:27 (anche i secondi cominciano ad avere importanza!), l’uomo moderno arriva due secondi prima delle 20:00. Una linea del tempo a misura di bambino!
Il tempo corre, la scadenza incombe e la mia mente è popolata di immagini, il mio quaderno contiene solo alcuni appunti pasticciati, ma ancora non c’è il percorso che dovrebbe essere oggetto di questo articolo per il Carnevale della Matematica!
Mumble mumble…
11 gennaio 2024, ore 22:30: una lunga giornata densa di avvenimenti volge al termine, la casa è avvolta nel silenzio, la scadenza per la consegna del link è a solo una manciata di ore da me (e vorrei anche dormire un po’ nel frattempo!).
Secondo quanto riportato da Annalisa Santi in Matetango, il calendario gregoriano (attualmente in uso) entrò in vigore con la bolla pontificia di Papa Gregorio XIII Inter Gravissimas, che cancellò di fatto 10 giorni dal calendario, dal 5 al 14 ottobre 1582: da giovedì 4 ottobre, si saltò direttamente a venerdì 15 ottobre. «L'idea iniziale era di saltare i primi dieci giorni di ottobre, a cui però i francescani si opposero per poter ricordare il 400° anniversario di San Francesco, nato nel 1182. Infatti, della nascita non si conosceva il giorno preciso e si ritenne di festeggiarla nella data liturgica del 4 ottobre, giorno successivo alla morte del 3 ottobre 1226.» Presente fin dall’inizio tra i mumble mumble che hanno caratterizzato le mie riflessioni sulla matematica bisestile, c’è il libro di Abner Shimony, pubblicato nel 2000, Tibaldo e il buco nel calendario. Tibaldo Bondi è il protagonista della vicenda e, all’epoca della bolla papale, ha quasi 12 anni: per la precisione, dovrebbe compiere gli anni il 10 ottobre del 1582, uno dei giorni cancellati dalla riforma gregoriana. Per i bambini i compleanni sono una tappa importante ed è per questo motivo che Tibaldo si accanisce a cercare una soluzione. Sullo sfondo la Bologna rinascimentale, le convinzioni medico-astrologiche dell’epoca e le consuetudini in ambito ostetrico, evidenti quando il protagonista accompagna la sorella Anna Maria nell’esercizio della sua professione. Alla fine, Tibaldo troverà una soluzione, come è giusto: perché la festività di San Francesco non può essere spostata, ma il compleanno di un dodicenne può essere cancellato?
Sto divagando…
Mumble mumble…
Riprendo in mano il post di Phil Plait e lo leggo con attenzione, poi un’ultima ricerca su Google: “Numberphile leap year”, perché non è possibile che il celebre canale non abbia fatto un video dedicato. E infatti eccolo! Un video pubblicato il 28 febbraio 2012, avente per protagonista l’astronoma Meghan Gray, che parla di questo anno bisestile come di un aggiustamento. Sembra di percorrere con lei la strada della scienza, un passo avanti e uno indietro, come in una danza alla ricerca della soluzione corretta. Il nostro percorso attorno al Sole si compie in 365 giorni e… briciole! Quantifichiamo queste briciole: sono 5 ore, 48 minuti e 46 secondi, quasi 6 ore, quasi un quarto di giorno. Anche le briciole, se sono corpose, possono avere una loro sostanza (lasciatevelo dire da chi è perennemente a dieta!) e sommando quattro di questi resti otteniamo quasi un giorno intero, per la precisione 23 ore, 15 minuti e 4 secondi. Mancano ancora 44 minuti e 56 secondi per fare un giorno intero, ma questo non impedisce di aggiungere un giorno intero ogni 4 anni: il 29 febbraio! Secondo il principio per cui anche le briciole contano, se moltiplichiamo questi 44 minuti e 56 secondi per 100 (tanti sarebbero i 29 febbraio nell’arco di 400 anni), otteniamo 3.12 giorni, abbastanza per scegliere di cancellare 3 anni bisestili e così gli anni che terminano con 00 non sono bisestili, se non nel caso in cui siano divisibili per 16, come riportato dettagliatamente nella spiegazione del sito della NASA, Leap day math.
12 gennaio 2024: questo flusso di coscienza sugli anni bisestili, con qualche spruzzata di matematica qui e là, sta giungendo al termine. Non so se ho rispettato le consegne o se sono andata fuori tema, ma secondo quando riportato in Matematti, il sito di appoggio per il Carnevale della Matematica, il tema «non viene necessariamente seguito dai partecipanti». Avendo aperto con un proverbio, concludo con un modo di dire bergamasco (anche se io l’ho sentito per la prima volta da mio suocero, bresciano), giusto per chiudere il CERCHIO: «Ol tép l’è töt tecàt», che letteralmente si traduce con “il tempo è tutto unito”, ovvero «I giorni si susseguono l’uno all’altro senza soluzione di continuità».
Per me è ancora un mistero: cosa significa realmente? Certi modi di dire sono più difficili della matematica!
Quanti? Tanti!
«Quanti? Tanti! Le potenze di dieci e la potenza delle domande» è stato pubblicato da Edizioni Dedalo, nella collana Scienza Facile, a novembre 2023. L’autrice, Sandra Lucente, è docente di Analisi matematica e di Comunicazione della scienza presso l’Università di Bari, fa parte del Comitato Scientifico del Museo della Matematica di Bari e dal 2007 si occupa di divulgazione, scrivendo articoli, tenendo conferenze e gestendo laboratori. Il libro è arricchito dalle illustrazioni di Fabio Magnasciutti, illustratore e vignettista, che ha vinto nel 2015 il premio come Miglior Vignettista presso il Museo della Satira di Forte dei Marmi, insegna Illustrazione editoriale presso lo IED di Roma e ha curato sigle e animazioni di alcuni programmi tv.
Il testo è costituito da 36 capitoli con la stessa struttura: l’apertura è con «Due immaginari curiosi, T&Q, acronimo di Tanti&Quanti, [che] si sfidano con domande un po’ “nerd”». Il dialogo, con precedenti illustri, è un po’ la cifra narrativa di Sandra Lucente, tanto che persino la bibliografia è presentata «in chiave dialogica». I due piccoli (?) protagonisti si fanno le domande “potenti” di cui parla il titolo, perché, come ribadito più volte: «le domande in matematica sono più importanti delle risposte». Al breve dialogo iniziale può far seguito una delle vignette di Magnasciutti, ma la parte centrale del capitolo è la lettera del personaggio famoso (non necessariamente un matematico) che risponde a T&Q. Con queste lettere, Sandra Lucente coglie l’essenza di ogni protagonista, calandosi in ogni epoca, con salti avanti e indietro nel tempo, ma usando un linguaggio attuale.
Il lettore, durante questo percorso, è invitato ad esercitare la pazienza, perché, come l’autrice fa scrivere a Ramanujan, «la matematica si conquista con carta penna e impegno»; bisogna inoltre superare le vertigini che si possono provare di fronte alle numerose informazioni presenti, e alla complessità necessaria per soddisfare le curiosità di T&Q. Se persevererà nel suo percorso, il lettore vincerà «il piacere della curiosità talvolta soddisfatta, talvolta stimolata [e] la partecipazione corale alla sfida del mondo complesso», ma queste “fatiche” saranno bilanciate dal senso di meraviglia e dai sorrisi che, qua e là, sono disseminati lungo il percorso.
Il cammino comincia con l’insieme vuoto, e procede con l’infinitesimo, risalendo poi le potenze di 10 da 10-30 fino a 1030, per poi concludere il percorso con il googol, il numero di Shannon, il megistone, il numero di Graham, cioè «il numero più grande che ha un significato per l’uomo», il numerabile e il continuo. È vero che «ogni capitolo si può leggere senza relazione con i precedenti», ma c’è un’unità di fondo, ben rappresentata dai tre diversi indici, che ci aiutano ad avere chiaro il percorso: il primo indice, «I numeri di questo libro», ci mostra le potenze di 10, con nome, prefisso e simbolo; il secondo indice, «I protagonisti di questo libro», in corrispondenza dei numeri mostra gli autori delle lettere, con l’anno di nascita e quello di morte; il terzo indice, quello classico alla chiusura del testo, ci mostra la potenza, il titolo e il sottotitolo del capitolo, nel quale ritroviamo il nome del mittente.
L’apertura di 60 ordini di grandezza ci mostra come nel tempo il nostro cervello abbia ampliato i limiti della propria conoscenza, estendendo il proprio universo, attraverso un maggior numero di unità di misura: da un lato, infatti, ci viene presentata la storia del Sistema Internazionale, con nuove grandezze e nuovi prefissi, ma, mostrandoci i numeri che costruiscono la realtà, ci ricorda che «occorre manipolarli correttamente per agire su di essa». L’obiettivo principale è forse «la riconquista di un sapere unico, il superamento degli ambiti disciplinari», perché la nostra realtà è sempre più pervasa di multidisciplinarietà e non si può restare chiusi nella propria bolla. Per questo motivo, i mittenti delle lettere non sono solo matematici: gli ordini di grandezza non hanno a che fare solamente con la fisica, non sono dominio numerico esclusivo della matematica, ma hanno a che fare con l’informatica e l’ingegneria, con l’economia e con l’archeologia. Ognuno di noi ha bisogno di possedere questi ordini di grandezza per poter comprendere la realtà.
Il percorso si apre con un filosofo, Bertrand Russell, e le sue scelte di libertà, si procede poi con gli infinitesimi di Isaac Newton (e il suo tono petulante è stato reso benissimo!) e con la bellezza della simmetria di Emmy Noether. Niels Bohr con la meccanica quantistica cede il passo all’originalità di Richard Feynman, mentre Mary Somerville, con le proporzioni, porta in primo piano l’amore per il pianeta. Nel prosieguo non può mancare Albert Einstein, che ci parla del Nobel per la fisica del 2023, a cui fanno seguito Maxwell con l’elettromagnetismo, Pascal con la probabilità, Marie e Pierre Curie con la radioattività, e Leonardo Sinisgalli, ingegnere autore di un cortometraggio. Nepero lega i logaritmi all’acidità, mentre Sofia Kovalevskaja ci offre le percentuali per capire la realtà, Poincaré sottolinea l’importanza dell’intuizione, laddove Pitagora e Fibonacci ci riportano alle origini, dall’incommensurabilità allo zero. L’archeologo Howard Carter apre la strada al secolo dei misteri, mentre Enrico Fermi mostra la ricchezza delle stime; il tuffo nel passato ci permette di incontrare Archimede, che parte da cose piccolissime per misurare l’universo, Ipazia mostra il potere dei libri e Li Ye ci porta al Milione di Marco Polo e alle Città invisibili di Calvino. Rita Levi-Montalcini ci apre alla ricchezza della mente, mentre Leibniz cerca un linguaggio universale nelle sequenze di zeri e uno; Paul Erdos apre al calcolo combinatorio con le disposizioni e con le poesie di Queneau, e Sophie Germain ci regala la controfigura della matematica; Alexander von Humboldt, naturalista e divulgatore, parla di insetti, mentre Ramanujan ci mostra le frazioni continue e le serie. Mendeleev gioca con le parole e crea la tavola periodica, e Hedy Lamarr ci ricorda di non lasciarci ingannare dai pregiudizi. Neil Armstrong mostra la potenza del lavoro di squadra e al-Khwarizmi non può che convincerci della necessità degli algoritmi per internet; Alan Turing parla del problema della decisione e dell’Intelligenza Artificiale, mentre Mandelbrot ci descrive la bellezza dei frattali. Frank Ramsey, con la sua breve vita, lascia un segno indelebile nella matematica e, mentre Galileo Galilei si perde nell’infinito, confrontando il tutto e la sua parte, Georg Cantor ci permette di orientarci tra gli infiniti, anche se non chiude realmente il percorso: non tutto in matematica è decidibile.
«All’inizio era un libro sui numeri grandi, poi è diventato un libro sui grandi della scienza» dichiara Sandra Lucente in apertura, mentre ci ricorda che il nostro cervello ha i limiti che sceglie di avere e, ogni volta che «diciamo “non mi piace la matematica” oppure “non mi piace la fisica” ci poniamo un limite e questo va contro il fatto di essere parte della specie che concepisce l’infinito». Sandra Lucente invita il lettore a mantenere la mente aperta e, attraverso le curiosità e le informazioni disseminate nel libro, studiato e curato in ogni particolare, aiuta il lettore ad amare la matematica e la fisica, offrendo spunti di approfondimento e facendo leva sull’umorismo delle vignette, che lasciano un’impronta indelebile nella nostra memoria.
La matematica della felicità
«La matematica della felicità» è stato pubblicato a settembre 2023 dalla casa editrice Piemme. L’autore è Rocco Dedda, docente di matematica con una tale passione per la sua disciplina da dedicarsi anche alla divulgazione, tanto da essere noto sui social come “Un quarto d’ora con il prof”. La sua attività di divulgazione è nata per caso, quando la sua Dirigente l’ha invitato a predisporre delle videolezioni per aiutare gli studenti a recuperare le proprie lacune in epoca pre-Covid, quando iniziative di questo tipo erano ancora rare. È nata da qui la scelta di aprire un canale YouTube e di usare i social per diffondere la sua passione per la matematica.
Fin dalle prime pagine, Rocco Dedda evidenzia come per gli insegnanti di matematica sia fondamentale «far capire agli studenti che la matematica non è un mostro che di notte si nasconde sotto il letto» ed è proprio per questo motivo che obiettivo primario del libro è tracciare «percorsi per imboccare la via d’uscita e accedere al mondo della matematica della felicità».
Il percorso si snoda in tre parti: la prima, intitolata «Non posso fare a meno di te», propone una serie di temi, perché il lettore si renda conto che la matematica è ovunque. Il contesto interdisciplinare proposto è particolarmente ricco perché, oltre alle solite applicazioni alla fisica, troviamo l’arte, la natura, la musica, la letteratura, fino ad arrivare all’orto, alla cucina e al turismo. Il messaggio che l’autore vuol far passare, quando si rivolge agli studenti, è che la matematica è davvero presente in vari ambiti della nostra vita, mentre per il docente, questo può essere foriero di spunti per approfondire tematiche interdisciplinari e collegamenti.
La seconda parte, intitolata «Capiamoci», è centrata sulla didattica ed ha un messaggio diverso a seconda del lettore: per gli insegnanti diventa una riflessione sulle difficoltà degli alunni ed offre motivazioni e strategie per arginare il problema; per gli studenti, diventa un aiuto per mettere i problemi nella giusta prospettiva. I capitoli che compongono questa parte sono delle piccole perle, che si prestano ad essere proposte ai propri studenti, per offrire spunti di riflessione e per promuovere la motivazione allo studio. Dedda convince il lettore che è possibile vivere felicemente la matematica, costruendo la propria autostima e opponendosi con convinzione alla matematica dell’infelicità, nella quale ci si imbatte anche a causa del fatto che la matematica è come «una ragnatela molto fitta che, con eleganza, intreccia dei fili», della quale la nostra mente deve cogliere l’intreccio, per poterla capire davvero. Dedda parla di «malesseri cognitivi» che possono avere diverse cause e diversi colpevoli, come lo studio discontinuo, le lacune accumulate nel tempo, la mancata comprensione di alcune proprietà, ma anche la relazione traballante tra insegnante e studente che può diventare un impedimento all’esternazione dei dubbi, e ricorda che «la consuetudine e l’esercizio sono fondamentali affinché la chiarezza dei concetti resista dentro di noi.»
Il capitolo intitolato «Il bivio» è, per quanto mi riguarda, una delle parti più preziose del libro, perché cerca di sondare le motivazioni che portano alla matematica dell’infelicità, ma, al tempo stesso, mostra come non ci sia un solo bivio e che si sia obbligati a compiere scelte in continuazione. Attraverso esempi pratici, che sanno tanto di vita vissuta, Rocco Dedda ci mostra quali potrebbero essere le tentazioni che spingono gli studenti a scegliere la matematica dell’infelicità, suggerendoci di intervenire per aiutare lo studente a compiere la scelta giusta, fornendo, «proprio con la matematica, momenti di felicità».
È così che si approda alla terza parte, «Come sei nata?», perché «La storia della matematica […] può essere il bilanciamento ideale per sprigionare la matematica della felicità». Rocco Dedda ci propone un percorso nel quale analizza gli aspetti principali della storia della matematica, fin dalle sue origini e, attraversando i secoli, approdando alle geometrie non euclidee e all’insiemistica. La carrellata si chiude con pi greco, i numeri primi e gli infiniti, ma soprattutto con un ultimo capitolo intitolato «La matematica (non) è un’opinione?». Si tratta di un’ode alla matematica che, secondo l’autore, «è un’opinione, ma allo stesso tempo non lo è».
Rocco Dedda ci permette di cogliere la bellezza della matematica: la descrive come «un complesso di confronti e bilanciamenti e il segreto per comprenderla, fino in fondo, è nella sintesi delle sue parti, nella capacità di esprimersi con la corretta armonia, tenendo conto di ciò che è e di ciò che potrebbe in alternativa essere; e imparando, prima di tutto, a comprenderla e a condividerla.» Riconoscendo i diversi approcci che caratterizzano il nostro rapporto con la matematica, ci offre una visione ricca di speranza: il mestiere dell’insegnante di matematica «è un lavoro da equilibristi», sempre in bilico tra la bellezza e la difficoltà. Con questo libro, Rocco Dedda ci aiuta a far pendere la bilancia in favore della bellezza, proponendo spunti agli insegnanti e guidando gli studenti nel proprio percorso. Un libro davvero per tutti!
Tubi, rose e... impacchettamento
A mia mamma piacciono tantissimo le rose di pesche: un po’ di pasta sfoglia (si compra in rotolo, già pronta!), qualche pesca, un paio di cucchiai di marmellata di albicocche e via in forno!
Per il suo compleanno, non potevano mancare…

Ne avevo fatte in quantità e ne sono avanzate 7. Le ho disposte su un piatto, nel modo più “economico” (in termini di spazio) possibile. È la pratica a indicare la strada, ma anche la matematica ci dà una mano:
«Chiunque deve disporre lattine di fagioli in un ampio spazio, può contare su un teorema matematico, noto come Teorema di Thue, secondo il quale la disposizione esagonale permette di raggiungere la massima densità possibile. Pertanto, ancora una volta, come spesso accade con i quesiti matematici, la soluzione migliore risulta essere fondata su una delle strutture più semplici e meglio conosciute.» (R. Eastaway, J. Wyndham, Matematica dietro le quinte, edizioni Dedalo).
Le mie non erano lattine, ma piccoli muffin di pesche, dalla forma tondeggiante, come quelle delle lattine!
Mio papà vede le rose sul piatto. Dice che gli ricordano la Tenaris… strano! Mio papà ha passato quasi tutta la sua carriera lavorativa alla Tenaris e qualsiasi cosa gliela ricorda. Ma questa volta ha ragione: la Tenaris produce tubi e, quando vengono stoccati, sono disposti in modo da occupare il minor spazio possibile, quindi seguendo una struttura esagonale (come quella delle lattine di fagioli!).
«Se il fascio di tubi era più grande, mi pare diventassero 19.»
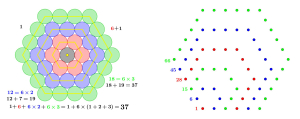
Il successivo numero esagonale è 19, ma sono numeri esagonali particolari, detti centrati. Così la disposizione dà la sequenza: 1, 7, 19, 37, 61, …
La si può costruire in questo modo: il primo numero è 1, poi si aggiunge 6, ovvero 6x1. L’esagono successivo ha i lati con 3 punti ciascuno, i vertici più il punto medio, perciò possiamo dire che l’esagono successivo avrà perimetro 12, in altre parole 6x2. Quello dopo ancora avrà 18 punti, cioè 6x3… e via così. Quindi, all’ennesimo esagono, avremo: 1+6(1+2+…+n-1), se consideriamo come primo esagono quello degenere e ridotto a un punto solo.
Erroneamente, avevo pensato ai numeri esagonali, ma i veri numeri esagonali sono quelli rappresentati nella figura a destra e la sequenza è diversa: 1, 6, 15, 28, 45, 66, …. Come si può notare, crescono più lentamente e danno luogo a un disegno diverso. Non solo: hanno una formula diversa! Io me la sono costruita e se vogliamo arrivare a 66, otteniamo:
1+(6x1-1)+(6x2-3)+(6x3-5)+(6x4-7)+(6x5-9)=1+6(1+2+3+4+5)-(1+3+5+7+9)=66
Slowmath
«Slowmath – Guida alla matematica non competitiva» è stato pubblicato nel 2015 dalla Casa Editrice Aracne. L’autore è Eugenio Biasin, docente di matematica alle scuole superiori, autore di numerosi articoli di didattica della matematica e del libro «Il prof sul lettino», pubblicato da Aracne nel 2010.
Già nell’introduzione l’autore dichiara che il suo obiettivo è quello di offrirci una visione originale della matematica, attraverso la «presentazione di idee matematiche belle, interessanti, di ampio respiro, interne alla disciplina o collegate ad altri aspetti della cultura». Con la prima di una lunga serie di citazioni, dà la parola a Imre Toth, matematico rumeno, che si dice indifferente da sempre «al lato sofisticato dei trucchi matematici. Quello che m’interessava era la struttura interna di questa complessa scienza».
Il libro è diviso in due parti: la prima parte, intitolata «Parole, immagini e protagonisti della matematica», offre un elenco di letture per cogliere la complessità e la bellezza della matematica. I cinque capitoli sono intitolati con lo stesso stile, ovvero quello di un aggettivo che precede l’oggetto del capitolo: così abbiamo «interessanti saggi», «piacevoli romanzi», «divertenti fumetti», «coinvolgenti pellicole» e «secolari congressi». Tra i saggi, raggruppati in biografie, problemi, argomenti e riflessioni, troviamo un elenco di una quarantina di testi, accompagnati da una breve descrizione e, a volte, da alcune citazioni. A questi fa seguito una trentina di romanzi, suddivisi tra ossessioni, vite, storia, filosofia, delitti, fantascienza ed enigmi, mentre il capitolo successivo è dedicato ai fumetti. L’elenco non è aggiornato, ma dà l’idea di un ambito in crescita, esattamente come il capitolo dedicato ai film. L’ultimo capitolo costituisce un collegamento tra le due parti: dopo una breve storia dei congressi internazionali, si parla delle medaglie Fields e dei premi che ad esse si sono aggiunti, come il premio Abel e il premio Gauss. Inevitabile, poi, parlare del Congresso di Seoul, avvenuto nel 2014, durante il quale è stata premiata Maryam Mirzakhani. Tra i numerosi vincitori della medaglia citati da Biasin, troviamo quello che, all’epoca della pubblicazione del libro, era l’unico premiato italiano, Enrico Bombieri, ma non manca una previsione (azzeccata!): «la situazione della ricerca scientifica nel nostro paese non è certo delle più rosee, ma di bravi matematici ne abbiamo eccome, molti dei quali attivi in università e centri di ricerca di primo piano nel mondo. Uno fra tutti Alessio Figalli…», vincitore della Medaglia Fields nel 2018.
La seconda parte è intitolata «Forme, numeri e idee» e offre una serie di percorsi, tra quelli ritenuti più significativi da Biasin, che si aprono con «La sorprendente relazione di Eulero». Dopo una riflessione sulla necessità dell’insegnamento della geometria, l’autore cita questo teorema, di natura topologica, e, dopo la dimostrazione, presenta tre interessanti conseguenze. «La misteriosa quarta dimensione» è oggetto del secondo capitolo, che si apre con una citazione tratta dal celebre «Flatlandia», e, dopo le rappresentazioni dell’ipercubo, approda ai politopi quadridimensionali. La conclusione del capitolo è dedicata a Mister Politopo, Donald Coxeter, matematico che ha contribuito allo sviluppo della geometria quadridimensionale. Da lui a Escher, il passo è breve, come scopriamo nel terzo capitolo, intitolato «Le meravigliose Coxeter-azioni di Escher»: le xilografie «Limite del cerchio» sono nate da una rappresentazione di Coxeter. Con «Gli intriganti segreti della moderna crittografia», l’autore non ha paura di darci definizioni rigorose e di guidarci nelle dimostrazioni, mentre un esempio ben orchestrato ci permette di capire il funzionamento dell’algoritmo RSA. L’ultimo passo è quello più coraggioso, da un punto di vista concettuale, visto che è dedicato a «L’inattesa incompletezza della matematica»: i celebri teoremi di Gödel guidano il percorso e ci riportano alle radici filosofiche della matematica.
La prima parte costituisce un’introduzione alla seconda, nella quale Biasin ci accompagna in un percorso studiato ad arte. Purtroppo, molti tra i numerosi suggerimenti di lettura della prima parte sono poco accessibili, se non grazie alle biblioteche: difficilmente i testi divulgativi di matematica diventano dei best seller («Il teorema del pappagallo» è più un’eccezione che una regola) e, se non li si acquista al momento della pubblicazione, diventa difficile reperirli quando è passato un po’ di tempo. Anche il testo di Biasin ha subito la stessa sorte e mi è stato possibile leggerlo solo grazie alla rete bibliotecaria. Personalmente, lo ritengo un ottimo approfondimento e, per gli insegnanti, l’occasione di accedere a un’esperienza trentennale, quella dell’autore: la sua scelta di condividere con il lettore una cultura costruita nel tempo non può che lasciarci meravigliati di fronte alla sua passione per la matematica.
Matematica dietro le quinte
«Matematica dietro le quinte» è stato pubblicato a giugno 2023 da Edizioni Dedalo, per la collana Senzatempo: è una nuova edizione di un testo del 2005, «Coppie, numeri e frattali. Altra matematica nascosta nella vita quotidiana», ora arricchito dalla presentazione di Elena Ioli. Gli autori sono Rob Eastaway e Jeremy Wyndham: il primo è un ideatore di giochi matematici per il «Sunday Times» e «New Scientist», che il secondo risolveva per passare il tempo. Eastaway ha ricevuto la medaglia Zeeman nel 2017 per la divulgazione matematica e in questa collana ha pubblicato anche Quanti calzini fanno un paio?, Wyndham è stato un regista indipendente e uno studioso di fisica. I due hanno scritto anche «Probabilità, numeri e code. La matematica nascosta nella vita quotidiana», attualmente di difficile reperibilità, perciò speriamo che Dedalo decida di procedere con una nuova edizione anche in questo caso.
Il testo è scorrevole e, pensato per i ragazzi delle superiori, è scritto con un linguaggio molto semplice e arricchito dalle illustrazioni di Barbara Shore, che non solo rendono più leggera la lettura, ma aiutano a spiegare meglio i concetti presentati. Ritroviamo, inoltre, alcuni box esplicativi che permettono di fare dei piccoli approfondimenti.
I sedici capitoli spaziano su tutta la matematica e sul mondo che ci circonda: si comincia con un esempio di come la matematica si nasconda tra le pieghe della nostra vita, visto che l’aritmetica modulare si nasconde nei nomi dei giorni della settimana, ma si esprime anche nel calendario lunare e nei dodici mesi. Troviamo trucchi e stratagemmi per spillare denaro, ma anche le indicazioni per scoprire le frodi e i raggiri, senza dimenticare che, purtroppo, «nessun sistema di controllo è infallibile». Nel terzo capitolo scopriamo come dar vita a un successo musicale, che poi viene straziato al karaoke, come ci spiega il quattordicesimo capitolo, dove gli autori citano Pitagora e Fourier, spaziando tra rapporti e funzioni goniometriche. E mentre impariamo a impacchettare efficientemente le cose e a trovare un posto per l’ultima valigia, se dobbiamo servirci di un taxi possiamo calcolarne la tariffa, mentre scopriamo la geometria del taxi e la probabilità di avere due compleanni coincidenti in un gruppo di persone. La strategia insita nella matematica può aiutarci con i quiz televisivi del quinto capitolo, ma anche a scegliere l’anima gemella, con un undicesimo capitolo dove fa capolino la probabilità. Il nono capitolo, dedicato ai meccanismi della diffusione di un’epidemia, parla di virus informatici, di infodemia e di modelli matematici, mentre nel sesto gli autori ci raccontano che anche gli ascensori hanno una logica, spesso in contrasto con l’irrazionalità degli utenti. La bellezza dei frattali mostra la sua utilità con internet e la borsa, ma sconfina nel caos, destabilizzandoci con previsioni del tempo non sempre esatte. Al tredicesimo capitolo fa capolino anche lo sport, dove la matematica aiuta a creare una maggiore spettacolarizzazione, influenzando i regolamenti o illudendoci, con un’errata applicazione della proprietà transitiva, di riuscire a prevedere l’esito di un incontro. Con simpatia e leggerezza, gli autori riescono infine a parlare dell’arte della dimostrazione, e a concludere il percorso con le falsità inventate dai manipolatori dell’opinione pubblica, che possiamo smascherare grazie alla matematica.
Con leggerezza e semplicità, gli autori portano allo scoperto la matematica che si nasconde tra le pieghe della nostra quotidianità, mostrandoci come le formule siano una comodità, quando ci permettono di effettuare calcoli veloci, applicandole persino in ambiti diversi da quelli in cui sono nate. La matematica coglie la struttura di fondo e collega ambiti apparentemente lontani, grazie alla sua versatilità e alla sua flessibilità. Il libro è davvero consigliato a tutti, in particolare ai non amanti della matematica, perché possano perdersi tra queste pagine, imparare che esiste una matematica diversa da quella studiata a scuola, appassionarsi.
Inscrivibilità e circoscrivibilità - IDM23
La proprietà dei quadrilateri di essere circoscritti a una circonferenza o di essere inscrivibili. Il rombo, con tutti i suoi lati congruenti, crede di essere superiore a chiunque, ma è solo circoscrivibile a una circonferenza; anche il rettangolo, con tutti i suoi angoli retti, crede di essere superiore, ma è solo inscrivibile in una circonferenza. Un quadrilatero qualsiasi, bullizzato dal rombo e del rettangolo, con tutti i suoi angoli e i suoi lati diversi, può essere sia circoscrivibile che inscrivibile in una circonferenza. Le apparenze ingannano.
Fumetto da me realizzato per partecipare alla Comic Challenge, organizzata per l'International Day of Mathematics 2023.
Matematica in pausa caffè
«Matematica in pausa caffè» è stato pubblicato dalla Codice Edizioni nel 2014 (comparso in una nuova edizione nel 2020) ed è il terzo libro di Maurizio Codogno, che si definisce, dalle pagine del Post, un «matematto divagatore». Maurizio ha scritto numerosi libri, «per raccontare le cose che a scuola non vi vogliono dire, perché altrimenti potreste apprezzare la matematica»: «Matematica in relax» (2011), «Matematica e infinito» (2013), «Fantamatematica» (2014), «Alfabeto matematico» (2015), «Matematica in pausa pranzo» (2016), «Scimmie digitali» (con Paolo Artuso nel 2018), «Numeralia» (2019), «Chiamatemi pi greco» (2022). Gli interessi di Maurizio Codogno sono molti e variegati, considerando che bazzica la rete dal 1984, è laureato in matematica alla Scuola Normale Superiore di Pisa e in informatica, è portavoce di Wikimedia Italia, lavora alla Telecom, e gestisce il blog xmau.com, dove si definisce un «tipo semplice», come si può intuire dalla grafica del sito, principalmente testuale.
«Matematica in pausa caffè» offre una serie di spunti che possono essere usati per chiacchierare di temi matematici curiosi, nel tempo necessario per bere una tazza di caffè, visto che ogni argomento è trattato in tre pagine (in media). Gli ambiti trattati sono cinque e per ogni ambito ci sono sette pause caffè. L’obiettivo dell’autore è quello di stuzzicare la curiosità del lettore, facendolo divertire e portandolo a comprendere in modo intuitivo le idee portanti, aiutandolo a «farsi un’idea della struttura logico-matematica di quello che ci circonda». D’altra parte, senza la matematica saremmo facili vittime delle bufale, come dimostra l’analfabetismo numerico dilagante. Gli argomenti sono trattati in modo da essere comprensibili anche ai non matematici, e mostrano come si possano «comprendere le idee matematiche anche senza mettersi a fare chissà quali calcoli».
Il primo ambito esplorato è quello dell’aritmetica, con la spiegazione del prodotto tra i numeri negativi, la differenza tra media, moda e mediana, la prova del nove che rimanda all’aritmetica modulare, la classificazione dei numeri – tra i quali individuiamo quelli «di dubbia fama», come gli irrazionali e i surreali – il paradosso di Zenone che ci porta alla distanza di Planck, i logaritmi e la crescita esponenziale.
Il secondo ambito riguarda i paradossi, la probabilità e le previsioni: Codogno parla della probabilità bayesiana partendo da un semplice esempio, ci racconta il paradosso delle due buste, il gioco di Penney legato al lancio di una moneta, il paradosso di Simpson e la legge di Benford, propone un problema di Fermi attuale domandandosi quanto peserebbe la stampa di tutta Wikipedia in lingua italiana e affronta la matematica delle coalizioni, citando il Nobel per l’economia Kenneth Arrow e ragionando sui modelli matematici, che, in quanto modelli, «considerano solo alcuni aspetti della realtà» e sono certamente «utili per avere un’idea, ma non necessariamente attinenti alla realtà».
Il terzo ambito è quello dei giochi, intesi come giochi d’azzardo ma non solo, con la probabilità che aiuta il ragionamento e risolve apparenti paradossi. Mentre Codogno ci ricorda che il banco vince sempre, ci suggerisce come “vincere” alla roulette (appunto: ma vincere quanto?) e dispensa consigli preziosi: «Non lasciatevi prendere dal panico di fronte a un problema, e iniziate a cercare una scorciatoia per giungere alla soluzione!». Ritroviamo la matematica anche nel tennis, dove a volte vince il peggiore, giochiamo con le carte e con i dadi, e scopriamo le dismutazioni che ci offrono un calcolo che assomiglia solo graficamente al fattoriale. In tutto questo, «la matematica è un utile ausilio, ma il mondo reale non è sempre così matematico… checché ne dicesse Galileo.»
Eppure la quarta parte, Andando in giro, sembra dirci che la matematica si nasconde ovunque: quella che viviamo è una realtà pervasa di contraddizioni, perché scopriamo che un tratto di tangenziale in più potrebbe peggiorare il traffico, che è sempre la corsia del supermercato che non scegliamo quella che ci avrebbe portato più velocemente alle casse, che i nostri amici hanno più amici di noi, che gli ascensori vanno sempre in senso inverso rispetto a quello che servirebbe a noi, che gli autobus hanno sempre lunghi tempi d’attesa e forse sarebbe meglio perderli, che il traffico si comporta come un’onda e che la «marcia dell’ubriaco» potrebbe portarci alla legge dei grandi numeri e nasconde in sé un pizzico di pi greco.
L’ultimo ambito di indagine non poteva che essere quello informatico: Codogno ci racconta il metodo di John Horton Conway che dal «giorno del giudizio» ci porta al calendario, ci insegna che per piegare un A4 in tre parti sono utili i triangoli simili, ci invita a diffidare dei file troppo compressi, ci dimostra che una crittografia perfettamente sicura è praticamente inutilizzabile, confronta i CD e i vinili, ci parla della nuova vita della steganografia, mettendoci in guardia dai gattini che frequentano la rete, e non può che concludere il cammino con i Big Data.
Il percorso che ci viene offerto da Maurizio Codogno mostra la sua originalità anche nel capitoletto finale, la bibliografia/sitografia che ci offre spunti «per saperne di più»: gli approfondimenti sono linkati attraverso un link TinyUrl, uno dei tool storici per i blogger, che ci dà un’idea dell’esperienza dell’autore (un po’ come coloro che usano l’acronimo LOL al posto della più nota emoji).
«Matematica in pausa caffè» ci offre una passeggiata attraverso vari ambiti della matematica, non sempre così noti: è un po’ come se la realtà si aprisse davanti a noi come la pagina di un sito e Maurizio Codogno ci offrisse un accesso al linguaggio di programmazione nascosto, permettendoci di apprezzare ancora di più la realtà che ci circonda. Il libro è davvero alla portata di tutti: si può leggere nell’ordine proposto dall’autore, per cogliere meglio i rimandi tra i singoli capitoli, oppure si può scegliere anche un ordine personale, visto che ogni capitolo è indipendente dagli altri.
Il libro è un vero regalo per gli insegnanti di matematica, che condividono la volontà dell’autore di far apprezzare la matematica ai propri alunni (e di alleggerire un po’ il percorso scolastico, a volte tedioso, scandito da equazioni e disequazioni).
Sette semplici lezioni di matematica
«Sette semplici lezioni di matematica», edito a ottobre 2020 dalla casa editrice Lindau, è l’ultimo lavoro di Francesco Malaspina, Professore Associato di geometria presso il dipartimento di Scienze Matematiche del Politecnico di Torino. L’autore vanta oltre una quarantina di pubblicazioni scientifiche su riviste internazionali, oltre al saggio divulgativo «Dio e l’ipercubo», pubblicato nel 2016 da Effatà.
Il testo è un piccolo saggio, suddiviso, come dice il titolo stesso, in sette capitoli. La prima lezione, dedicata all’intuizione e all’astrazione, comincia con una profonda verità: «La matematica non lascia indifferenti. Se ne può rimanere folgorati e innamorarsene follemente. I più però ci tengono subito a precisare, quasi come fosse un vanto, che non ne hanno mai capito assolutamente nulla.» D’altra parte, alla matematica possiamo associare una vasta gamma di termini: fredda, spietata, male necessario, ma anche bellezza, arte, poesia e fantasia, tant’è che l’autore stesso ci dice che i matematici «seguono una scia di bellezza», perché «gli oggetti matematici non solo hanno a che fare con l’arte, ma sono essi stessi opere d’arte». La seconda lezione va ad indagare i fondamenti della matematica, ovvero gli insiemi, partendo dal fatto che «la matematica è grande come tutta la cultura in generale» anche se non può offrire spiegazioni a tutto, perché «ci sono degli aspetti nella nostra vita, spesso quelli più profondi, nei quali non ci possono essere dimostrazioni», come Gödel ci ha insegnato con l’incompletezza. La terza lezione è dedicata alle strutture algebriche: si comincia con la descrizione dell’amore e delle sue proprietà, attraverso Frozen, Dante e Gabbani e questa «spericolata analogia», come la definisce l’autore, tra amore e matematica vede nelle somme la prima esperienza della matematica che ci apre le porte a una maggiore astrazione, con la teoria dei gruppi e le simmetrie. La quarta lezione prende spunto dal calcio, non solo per i vettori che diventano un mezzo per realizzare gli schemi calcistici, ma anche perché nella matematica, come nel calcio, «ci vuole il coraggio di un inserimento audace quando si tentano strade un po’ spericolate, o pazienza nella fase di non possesso quando ci sembra di non avere l’idea giusta e la nostra ricerca attraversa una fase stagnante.» Non dobbiamo in effetti dimenticare che il sottotitolo di questo testo è “d’amore, morte, calcio, meringhe e geometria” e ritroviamo tutto equamente distribuito all’interno del testo. L’itinerario di questa lezione, probabilmente la più impegnativa e approfondita, viene ripreso in chiusura e sottolineato con una ulteriore metafora calcistica, dove il calcio viene usato come esempio di gioco corale esattamente come la «meravigliosa, sublime sinfonia matematica». La quinta lezione ci presenta la potenza del calcolo infinitesimale e dell’analisi matematica, partendo, apparentemente in modo paradossale, dalle meringhe. La sesta lezione è dedicata alla geometria della gomma, ovvero alla topologia, e si passa attraverso l’amore per giungere poi all’infinito. L’ultima lezione è dedicata alla matematica applicata, ma è un piccolo assaggio di quello che potremmo esplorare grazie alle equazioni differenziali.
«Gli oggetti matematici comparsi nelle varie lezioni possono apparire, a prima vista, appartenenti a mondi lontani. Quando ci si addentra più in profondità, però, si scopre come sappiano interagire tra loro efficacemente e come siano strutturalmente simili.» La matematica viene presentata così grande ed eccezionale da poter far parlare di qualsiasi cosa perché è un linguaggio universale. Nella lettura si ritrovano citazioni da “Il senso di Smilla per la neve” e “La storia infinita” di Michael Ende, sono citati la Mannoia, Gino Paoli, Venditti e Jovanotti, in un'interdisciplinarietà necessaria, ma giocosa e al tempo stesso «ricchezza per tutti gli attori coinvolti». Per questo e per molti altri motivi, la lettura è consigliatissima agli insegnanti di matematica, ma anche a quegli studenti universitari che si addentrano per la prima volta nell’astrazione dell’algebra lineare o rischiano di perdersi nei meandri dell’analisi e possono quindi tenersi ancorati alla realtà e osservare il panorama dall’alto.
«La matematica è in grado di parlare dei sentimenti più profondi e intimi, così come dei fenomeni della natura e delle invenzioni della tecnologia. Riesce a essere contemporaneamente bellezza artistica e freddo algoritmo. È un linguaggio universale, misterioso e fecondo, che non finirà mai di stupirci.»
© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy