Visualizza articoli per tag: Carnevale della matematica
Errori del 2025
Come uno studente davanti al titolo del tema, osservo il foglio bianco davanti a me e non so cosa scrivere.
2025 è il tema di questo Carnevale.
Da quando è cominciato il nuovo anno, mi sono piovuti addosso video e messaggi di tutti i tipi: dal teorema di Nicomaco di Gerasa, dimostrato per induzione dal canale Mathematical Visual Proofs (e condiviso con la scorsa newsletter), alle varie catene girate anche su Whatsapp, vista la “magia” di 2025, quadrato perfetto, ma anche difettivo. Cosa si può aggiungere di davvero originale a questo anno definito matematico, matemagico e chissà in quale altro modo matematico-riferito?
Osservo le cifre di 2025: posso scrivere 12 numeri diversi, il più piccolo 0225 e il più grande 5220, ma ci sono solo due quadrati, 0225 e 2025, e la somma delle cifre è 9. Quest’ultima affermazione era prevedibile, visto che 2025 è divisibile per 9, ma, per qualche motivo, questa cosa mi resta in testa.
2+0+2+5=9
9
Come la prova del 9… raccontata così bene nel libro di Bruno Jannamorelli La misteriosa prova del 9.

Ho scoperto solo in tempi recenti che la prova del 9 si può applicare anche all’addizione, alla sottrazione e alla divisione, oltre che alla moltiplicazione (l’unica che conoscevo e applicavo). La prova permette di individuare gli errori di calcolo, ma nasconde anche tanto altro e vale la pena riprendere qui il discorso presentato nella newsletter #172 del 23 aprile 2021: Davide e Riccardo del MATH-segnale, dopo essere partiti dalla prova del 2, mostrano i passaggi della prova del 9 per la moltiplicazione, con la collaborazione di Gianluca Zanzottera, e poi procedono a mostrare per quale motivo si basi il ragionamento sul resto del prodotto dei resti, per verificare la correttezza del risultato.

Nella descrizione trovano posto sia il calcolo letterale che l’aritmetica modulare, con dovizia di particolari e chiarezza. Oltre alla prova del 9 per l’addizione spiegata da Gianluca Zanzottera, nella newsletter ho condiviso anche un bellissimo articolo di Alberto Saracco, scritto per MaddMaths!, Apologia delle prove, nella quale il noto divulgatore spiega innanzi tutto perché non sia il caso di utilizzare la calcolatrice per verificare un calcolo e mostra poi come anche la calcolatrice che sembra più affidabile, come il foglio elettronico di Excel, sia in realtà facile agli errori. Alla paura di sbagliare, leva degli spesso maldestri tentativi di evitare il calcolo, dedica un intero paragrafo: «Abbiamo tutti un’enorme paura di sbagliare. Ci piace mostrarci bravi e infallibili. Ammettere la nostra fallibilità e i nostri errori è spesso un problema. Però sbagliamo tutti. Ed è naturale sbagliare. Anzi, può essere persino utile. Senza errori non impariamo. In effetti se non facciamo mai errori, vuol semplicemente dire che stiamo facendo cose troppo facili e non ci stiamo impegnando su qualcosa di sufficientemente stimolante. Spesso inoltre la scoperta di un errore può essere da guida per vedere qualcosa sotto una nuova luce e imparare qualcosa di nuovo. Per poi sbagliare ancora, ma sbagliare meglio.» Anche Alberto Saracco dedica grande attenzione alle prove di verifica, come la stima dell’ordine di grandezza e la prova dell’11, ma mi piace in particolare ciò che il professore dice ai propri studenti: «Tutti possono commettere stupidi errori di conto, ma se non sprechi 30 secondi per fare una prova banale che ti avrebbe fatto scoprire che hai fatto un errore, non è più un banale errore di conto, ma è qualcosa di più grave.» Prima di chiudere ricorda che la verifica dei risultati è un modo per «acquisire una competenza matematica».

Al primo gennaio, fatico a sentire l’ansia e l’eccitazione dei nuovi inizi: per me, complice il ritmo dell’insegnamento, il vero inizio è quello dell’anno scolastico, che si apre il 1° settembre. Ogni inizio è carico di aspettative per ciò che dovremo affrontare, e non mancano previsioni (astrologiche o meno) per riuscire in qualche modo a rassicurare tutti noi in merito al futuro che ci aspetta. Personalmente ritengo che ogni nuovo anno regali una sola sicurezza e mi piacerebbe in tal senso rubare e parafrasare «The paradox of the preface» citato da Piergiorgio Odifreddi nel libro C’era una volta un paradosso. Se consideriamo i primi giorni di gennaio come l’introduzione del nuovo anno, potremmo dire che questo anno conterrà almeno un errore e si tratta di una facile previsione, in effetti. Ci si potrebbe aspettare che per sapere se ci saranno errori nel corso dell’anno sia necessario arrivare alla fine, ma invece lo sappiamo già fin dai primi giorni che ci saranno errori (e non solo perché, probabilmente, ne avete già fatti a profusione come me…): infatti, se ci sono errori, ci sono. E se non ce ne sono, l’errore sarà stato quello di dire che quest’anno conterrà almeno un errore.

Speriamo di riuscire a individuarli con una semplice prova del 9, ma, in ogni caso, che il 2025 possa essere un anno ricco di errori, matematici e non, perché, come ricorda Alberto Saracco: «Senza errori non impariamo. In effetti se non facciamo mai errori, vuol semplicemente dire che stiamo facendo cose troppo facili e non ci stiamo impegnando su qualcosa di sufficientemente stimolante».
PS: Ho appena finito questo breve post e, mentre sto cercando immagini da inserire che richiamino l'errore scrivo "errore" in Google immagini e mi imbatto nell'articolo del 27 dicembre 2020 di Vittorio Pelligra scritto per Il Sole24Ore, dal titolo Perché sbagliare non sempre è un errore. Pelligra ha usato il tema dell'errore per «rappresentare in modo sintetico ma evocativo questo anno passato [il 2020], così anomalo e tragico ma, allo stesso tempo, anche foriero di novità e timide speranze [...] un tema che, contemporaneamente, potesse offrire la possibilità di riflettere [...] sulle sfide che il futuro prossimo ci presenta, sui rischi e sulle opportunità che ci si pongono innanzi e che dovremmo al più presto iniziare a sfruttare al meglio». Buona lettura!
Un'insegnante di matematica
Un capomastro lavorava da molti anni alle dipendenze di una grossa società edile. Un giorno ricevette l’ordine di costruire una villa esemplare secondo un progetto a suo piacere. Poteva costruirla nel posto che più gradiva e non badare alle spese.
I lavori cominciarono ben presto. Ma, approfittando di questa cieca fiducia, il capomastro pensò di usare materiali scadenti, di assumere operai poco competenti a stipendio più basso, e di intascare così la somma risparmiata.
Quando la villa fu terminata, durante una festicciola, il capomastro consegnò al Presidente della società la chiave d’entrata.
Il Presidente gliela restituì sorridendo e disse, stringendogli la mano: «Questa villa è il nostro regalo per lei in segno di stima e di riconoscenza».
Bruno Ferrero, «C’è qualcuno lassù?», Editrice Elle Di Ci
Quando Marco Menale ha lanciato il tema di questo Carnevale della Matematica, «Matematica e Futuro», ha detto di declinarlo come si preferiva: «tempo verbale, congetture da risolvere, nuove teorie, IA, vita su Marte ecc ecc». Dopo qualche giorno di riflessione, ho realizzato che, in quanto insegnante, il futuro lo tocco con mano ogni giorno, contribuendo a plasmarlo, ma cosa può avere a che fare questo con la matematica?
Nel momento in cui ho scelto il mio di futuro, non ho scelto solo di studiare matematica e non ho scelto di fare l’insegnante, ho scelto di fare l’insegnante di matematica: le due cose sono state, per me, inscindibili da subito. Quando ho fatto questa scelta, frequentavo le scuole medie e avevo un’idea molto limitata della matematica: fondamentalmente, mi piaceva svolgere espressioni e piccoli problemi, e ho mantenuto la passione anche al liceo, nonostante abbia riflettuto ultimamente su quanto sia più facile far amare la fisica, rispetto alla matematica. La fisica si presenta, almeno all’inizio, con una veste abbastanza semplice, richiedendo poco più dell’algebra per la soluzione di problemi che descrivono una realtà ovattata. Eppure, anche se limitata da piani senza attrito e moti perfettamente uniformi, la fisica conquista e affascina, perché tenta una descrizione della realtà. Ben diverso è il percorso della matematica, che mostra fin da subito il suo lato spinoso. Chi si diverte con il calcolo, spesso prosegue alle superiori con l’algebra senza troppi intoppi, ma chi rifugge il rigore, rischia di restare incastrato nei meccanismi del calcolo letterale. Poi ci si scontra con la geometria analitica e con i problemi: da studenti che subiscono passivamente equazioni e disequazioni, gli alunni sperimentano quanto diceva Maryam Mirzakhani, «Fare matematica per me è come una lunga escursione senza un sentiero tracciato né un traguardo visibile». All’ultimo anno poi, lo studio di funzione costituisce l’apice del percorso e dell’astrazione, ed offre l’opportunità di effettuare quegli approfondimenti che non hanno trovato spazio in precedenza. Ma l’esame di stato è alle porte e, che si sia studenti in un liceo scientifico oppure no, tutto viene assorbito da quello e non resta spazio per far amare questa splendida disciplina. E così, anche noi insegnanti in qualche modo diventiamo oggetto di questo odio, che non si capisce più se nasca contro la matematica e poi si estenda anche a noi, o se siamo noi insegnanti che non siamo capaci di generare simpatia, né per noi né per la nostra disciplina.

Temo che questo “odio” abbia a che fare con la richiesta di semplificazione che arriva da più parti, una sorta di ricerca di riassunti, schemi, che possano aiutare a capire, ma, al tempo stesso, rendere più veloce il tempo di apprendimento. Credo che la chiave del problema sia proprio in questa “fretta”: il processo di apprendimento in generale, non solo quello della matematica, richiede tempo e pazienza e, a volte, costa fatica, e cercare di spianare la strada ai nostri alunni non li aiuta a imparare. Qualcuno più famoso di me, e molto prima di me, l’ha detto meglio: «Non esistono vie regie»!

Sono consapevole di non essere la sola a vivere questa fatica, come ha ben dimostrato su Facebook un post del 15 ottobre scorso di Giuseppe Mingione, docente di Analisi all’Università di Parma: dopo aver richiesto la soluzione di un semplice esercizio ai suoi studenti e non averne ottenuto alcuna risposta, l’ha somministrato a ChatGPT, ottenendone una soluzione perfetta. Ha quindi chiesto ai suoi studenti che compito si assumerebbero e quale affiderebbero a ChatGPT, tra risolvere esercizi e raccogliere pomodori: «i ragazzi hanno stavolta correttamente risposto, e, preoccupati, hanno capito cosa sta succedendo».

Non ho potuto non parlare in classe di questo post, invitando i miei studenti a riflettere sul fatto che la scelta di studiare determinati argomenti ci permette di ampliare il ventaglio di possibilità che il futuro ci offre. Resto sempre un po’ perplessa quando, arrivati all’ultimo anno di liceo, alcuni miei alunni, posti di fronte alla scelta del percorso da seguire all’università, vanno alla ricerca del corso di laurea che non prevede un esame di matematica. Ho ritrovato questo mio malessere ben argomentato, proprio ieri, da Federico Benuzzi, che ha raccolto, al termine di un suo spettacolo, la frase, pronunciata da un alunno di una terza media: «Andrò al linguistico perché c’è poca matematica». Benuzzi dà voce a questa frustrazione scrivendo: «il percorso di studi si sceglie “per”, non “contro”».

Quando dico che, come insegnante, plasmo il futuro, non mi riferisco, però, solo al futuro dei miei studenti: a loro tento di dare quegli strumenti che, credo, saranno fondamentali non solo per la loro professione, ma per la loro vita, e nel costruire qualcosa per loro costruisco anche qualcosa per me, come il capomastro del racconto iniziale. Il mio pensiero torna a quel giorno in cui, in pronto soccorso, sono stata accolta da un ex alunno che lì lavorava come infermiere: quando guardo i miei alunni, nell’età più ingrata della loro vita, cerco di non dimenticare che un domani saranno adulti, e potrebbero essere direttori/direttrici della casa di riposo in cui passerò gli ultimi anni della mia vita.
Facendo l’insegnante di matematica, sento di contribuire a costruire la vita dei ragazzi attraverso la matematica, anzi sono consapevole che sarà proprio la matematica ad offrire loro una vita diversa. Sempre citando Giuseppe Mingione: «una maggiore alfabetizzazione matematica serve anche a difendersi da certe frottole ben raccontate».
Abraham Lincoln, politico e avvocato statunitense nonché sedicesimo presidente degli USA, scrisse una celebre lettera all’insegnante di suo figlio il primo giorno di scuola. Alla ricerca di idee per questo articolo, non potevo non restare colpita da questa edizione per bambini della Einaudi, suggerita sul suo profilo Instagram da Alessandro Barbaglia, autore de L’invenzione di Eva, romanzo e biografia di Hedy Lamarr: «Gli insegni, se può, che 10 centesimi guadagnati valgono molto di più di un dollaro trovato; a scuola, o maestro, è di gran lunga più onorevole essere bocciato che barare.» La scuola è un ambiente protetto, nel quale è importante che vengano proposte sfide, anche al di sopra delle proprie capacità: è come una palestra nella quale ci si allena a vincere le gare della vita, costruendo strumenti importanti per il futuro.

Rileggendo ciò che ho scritto fino ad ora, mi rendo conto che nella mia vita la matematica, forgiando il mio passato, mi ha permesso di costruire un presente nel quale ho il potere di plasmare il futuro. In altre parole, posso declinare la matematica al passato, al presente, al futuro, ma credo che, consapevoli o meno, sia una cosa che ognuno di noi può fare. Mentre ascoltavo la TED-talk di Alberto Saracco, docente di geometria all’Università di Parma, intitolata Matematica per il futuro, riflettevo non solo sull’impossibilità di studiare solo ciò che può essere utile un domani (come si fa a sapere cosa ci sarà non solo utile, ma necessario?), ma mi ponevo anche un’altra domanda: dove si deve fermare lo sguardo? Quando insegno, il mio sguardo non si ferma all’orizzonte dell’esame di stato, ma va oltre, e credo che lo sguardo di un matematico sia simile: i matematici hanno trovato il modo di toccare l’infinito (basti pensare al piano proiettivo), e allo stesso modo possono toccare il futuro, come dimostrato dalla trasformata di Radon-Nikodym del 1917, che è diventata la chiave per uno degli esami diagnostici più importanti, la TAC. Chi avrebbe potuto vedere un futuro così brillante in una matematica così complessa e, per i più, oscura? È sempre Alberto Saracco, nel parlare della ragionevole efficacia della matematica, che dice: «La matematica è potente nel descrivere il mondo e chi sa utilizzarla per il proprio tornaconto ha a disposizione un vantaggio enorme».

Insegno matematica e plasmo futuro ogni volta che propongo sfide, ogni volta che chiedo ai miei studenti di ragionare, ogni volta che stimolo uno sguardo critico sulla realtà, ogni volta che chiedo un piccolo impegno continuo, perché il futuro non si improvvisa, esattamente come una verifica di matematica. Non mi faccio illusioni, però: non ho idea di quanto loro ricordino di ciò che cerco di trasmettere, ma ho imparato che, se dico qualcosa di errato durante una spiegazione (e lo faccio più frequentemente di quanto vorrei), loro lo ricorderanno sicuramente. Purtroppo, questi errori hanno una vita lunga, come dimostrato dal video realizzato pochi giorni fa dal canale Kurzgesagt – In a Nutshell. Il titolo del video rimanda alla «più vecchia bugia di Internet» e racconta della ricerca delle fonti per la frase: «I tuoi vasi sanguigni si estendono per l’incredibile lunghezza di 100.000 chilometri, abbastanza da avvolgere la Terra due volte!» Ci è voluto un anno per trovare l’origine di questa affermazione e non voglio rovinare la sorpresa, ma basti sapere che l’affermazione è nata, innanzi tutto, da una serie di approssimazioni, e si trattava di una cosa di poca importanza inserita in un libro che aveva ben altri meriti. Eppure, ciò che ha trovato la strada per Internet, da un libro di oltre un secolo fa, è stata un'affermazione sbagliata.

Carnevale della matematica #180
“Canta canta, il merlo, il merlo tra i cespugli”
(poesia gaussiana)
Benvenuti all’edizione numero 180 del Carnevale della matematica!
Come i precedenti, il numero 180 è introdotto dalla consueta CELLULA MELODICA predisposta da Dioniso Dionisi che l’ha definita una «cellula melodica con un’armonizzazione minimalista».
180 è, evidentemente, un numero pari, e, come evidenziato dalla poesia gaussiana sopra riportata ha cinque fattori primi: 2 (che corrisponde a “canta”), 3 (che corrisponde a “il merlo”) e 5 (che corrisponde a “tra i cespugli”). Le ripetizioni della cellula melodica (e la fattorizzazione imparata alla scuola secondaria di primo grado!) ci fanno dire che 180 è dato da 2x2x3x3x5. La somma dei suoi divisori (sono 18) è 366, perciò 180 è un numero abbondante, ma è anche l’undicesimo numero altamente composto, che significa che ha più divisori di tutti i numeri che lo precedono (il prossimo sarà 240). Tra le curiosità a mio avviso più belle che emergono dal web cercando 180:
- è un numero di Harshad nel sistema numerico decimale, cioè è divisibile per la somma delle sue cifre. La definizione di questo numero risale al matematico indiano Dattaraya Ramchandra Kaprekar (1905-1986): lavorò come insegnante per tutta la sua carriera, ma pubblicò diversi articoli di matematica ricreativa. Secondo Wikipedia, il termine Harshad deriva dal sanscrito “harṣa” che significa “grande gioia”;
- è la somma di sei numeri primi consecutivi: 180 = 19 +23 + 29 + 31 + 37 + 41;

- è il numero che indica alcune strade negli Stati Uniti, ma a me piace ricordare la Interstate 180 dell’Illinois, che va da Princeton a Hennepin, per un totale di poco più di 21 km (anche se non è la Princeton che tutti conosciamo, quella della famosa Università e di Einstein, che è nel New Jersey);
- la Vespa 180 Rally della Piaggio è stata prodotta tra il 1968 e il 1973 in 26.000 esemplari

Visto che mi sto perdendo in campo automobilistico, non posso non citare l’«inversione a U», che può essere indicata come una svolta di 180°. È abbastanza comune, quando si nomina 180, pensare all’angolo piatto, indicato in radianti come p, e direi quindi che è il caso di passare al primo post (che non è esattamente in tema, ma a suo modo sì), che tratta della Sezione Aurea e di un’identità dove compaiono contemporaneamente alcune delle più importanti costanti matematiche. Essendo formule che contengono Pi Greco, ecco trovata la prima connessione con il #180. Il post è di Mauro Merlotti dello Zibaldone Scientifico e si intitola Formule complesse.
Il tema scelto per questa 180^ edizione del carnevale è Matematica e sport, ispirato da questa estate di Olimpiadi e Paralimpiadi, da un mondo dello sport sempre più ricco di matematica e da una matematica che può offrire sempre più risorse anche allo sport.
Comincio il Carnevale settembrino dando la precedenza ai matematti che hanno scritto qualcosa in tema. La prima a rispondere alla chiamata è stata Annalisa Santi, che ha dedicato il proprio contributo al grande campione Francesco Molinari, l’uomo che il 22 luglio 2018 entrò nella storia del golf. «Con questo articolo avevo voluto fare un omaggio al grande golfista che vinse l’Open Championship scozzese, il più antico e celebre dei Major, lasciando così a Carnoustie, per la prima volta dal 1860, il nome di un atleta italiano, e, nello stesso tempo, parlare di questo stupendo gioco del golf e di un po’ della matematica che vi si cela.»

Mauro Merlotti, dalle pagine dello Zibaldone scientifico, parla del fotofinish, uno «strumento indispensabile per molte gare sportive; potrebbe sembrare una fotografia, ma mentre questa è la riproduzione un oggetto ad un determinato istante (almeno in prima approssimazione), il fotofinish riproduce un oggetto ad una determinata posizione (con scorrimento continuo della pellicola)».
Nel suo blog Gli studenti di oggi, Roberto Zanasi propone un post senza tante parole, con un grafico della classifica delle Olimpiadi costruito con «un ordinamento parziale in cui uno stato X è stato migliore di un altro stato Y se il medagliere di Y può essere trasformato nel medagliere di X mediante una sequenza di aggiunte di medaglie oppure di sostituzione di medaglie basse con medaglie alte.»
Paolo Alessandrini, autore di Matematica in campo, non poteva far mancare il proprio contributo a questa edizione del Carnevale e infatti ci regala ben sei post, quattro in forma di “shorts” e due in forma di video più lunghi e articolati. I link rimandano al nuovo blog Paolo Alessandrini – Racconto la matematica in più modi: sono autore, divulgatore, docente. Ecco l’elenco dei link, descritto direttamente da Paolo:
- Dalle origini a EURO 2024: storia e geometria dei palloni da calcio: Un viaggio attraverso l’appassionante storia dei palloni da calcio, con particolare attenzione alle questioni geometriche
- Eurogoal a effetto: dal cucchiaio di Totti al tiraggiro di Zaccagni: Curiosamente, molti dei più famosi tiri a effetto della nostra Nazionale di calcio sono andati in scena durante edizioni del campionato europeo: ecco la matematica e la fisica che sta dietro queste prodezze.
- Olimpiadi, che palle! Uno short dedicato ai vari tipi di palla utilizzati nelle specialità olimpiche.
- La matematica di Marcell Jacobs: Uno short sul teorema di Lagrange applicato ai 100 metri olimpici.
- La matematica (e la fisica) di Gimbo Tamberi: Uno short sulla matematica e sulla fisica del salto in alto.
- La formula rivoluzionaria della Champions League 2024-25: Uno short sulla nuova formula della Champions League, molto curiosa dal punto di vista combinatorio.

Per i contributi di MaddMaths! comincio dai due contributi realizzati sulla scia degli ultimi europei di calcio, lasciando a loro la parola:
- EURO 2024: l’europeo dei dati Euro2024 ha visto la vittoria della Spagna in finale contro l’Inghilterra. Oltre che in campo, questo campionato europeo si è giocato tra numeri, algoritmi e dati. Ce ne parla Marco Menale per la rubrica La Lente Matematica.
- Il tabellone ad eliminazione diretta degli Europei: una scelta non ottimale? Sono finite le partite dei gruppi di Euro2024 e sta per iniziare la fase ad eliminazione diretta. Olanda e Austria potrebbero rincontrarsi già ai quarti di finale!! Com’è possibile? È un errore? Cesco Reale (divulgatore ludo-scientifico: ecco la sua divulgazione matematica e quella ludica) e Alberto Saracco provano ad approfondire, per capire meglio come il ragionamento matematico possa portare alla creazione di tornei più equi.

E, poi, un paio di extra sul tema, dall’archivio di questo 2024:
- Marco Menale ha raccontato in tre episodi de La Lente Matematica cos’è l’xG – expected goals, e come questo parametro si colleghi all’angolo di tiro e all’angolo Kos, ossia l’angolo di tiro considerando gli avversari presenti di mezzo.
- Le leggi di Newton aiutano a nuotare meglio Cento anni fa, alle Olimpiadi di Parigi del 1924, l’americano Johnny Weissmuller vinse i 100 metri di stile libero maschili con un tempo di 59 secondi. Quasi un secolo più tardi, nelle Olimpiadi di Tokyo 2020, Caeleb Dressel, sempre nello stesso stile, portò a casa la medaglia d’oro rosicchiando 12 secondi a Weissmuller. I tempi, in questo sport, sono significativamente migliorati negli anni come risultato combinato di diversi fattori di innovazione applicati all’allenamento, alla strategia di recupero, alla nutrizione, nonché all’uso di più moderne attrezzature. Ma un ruolo chiave, in questi progressi, va riconosciuto sicuramente alla biomeccanica della bracciata, che ha consentito di ottimizzare le tecniche natatorie in ogni stile. Negli anni ultimi, l’integrazione di principi matematici e scientifici e l’uso di sensori indossabili ha ulteriormente perfezionato le prestazioni degli atleti, come dimostrano i risultati della squadra di nuoto dell’Università della Virginia (UVA), capitanata dall’allenatore Todd De Sorbo ed assistita da Ken Ono. Ce ne parla Stefano Pisani per le News.
Tra le varie proposte pervenute da Gianluigi Filippelli per il suo blog DropSea, c’è l’articolo Inseguimenti in pista, a tema Formula 1, per la serie dei Paralipomeni di Alice: il problema è proposto da Maurizio Codogno nel 22° volume della serie Matematica della Gazzetta dello Sport ed è una bellissima idea da proporre in classe. Siccome il post è stato pubblicato in occasione del Gran Premio d’Ungheria, Gianluigi si è divertito a cercare le due velocità che permettono le prestazioni riportate nel problema proprio sul circuito d’Ungheria, scoprendo risultati a dir poco fantascientifici, per delle auto da corsa.
I matematti difficilmente riescono a stare nei confini di un tema, forse perché la matematica stessa va ben al di là dei limiti imposti, perciò non sorprende che i contributi di altri argomenti superino di gran lunga quelli che parlano di sport. Procediamo quindi con Dioniso Dionisi, che ci offre la prima parte di Archita, Platone, Eudosso e la duplicazione del cubo. Si tratta, secondo le parole dell’autore, di «un dialogo in cui il giovane Eudosso illustra a Platone, in visita a Taranto, la soluzione del suo maestro Archita per la duplicazione del cubo.» Eccone un estratto: “«Ah, conosco bene la duplicazione del cubo», replicò subito il giovane. «Il maestro Archita ha preteso che la studiassimo a fondo. Anche perché… la vera soluzione è sua. Quella di Ippocrate è insufficiente perché semplifica il problema ma non lo risolve. Invece il mio maestro ha trovato la soluzione concreta e non solo teorica, come quella di Ippocrate». «E… quale sarebbe questa soluzione concreta?», chiese Platone con circospezione.”
I contenuti di Maurizio Codogno sono tantissimi, come sempre. Eccoli, presentati da lui stesso e distinti per categoria.

Cominciamo con i volumi della collana Matematica:
- 19 – L’analisi matematica, di Salvatore Fragapane: risposte a domande che non vi siete mai fatti sul perché si studia analisi.
- 20 – La teoria dell'informazione, di Maurizio Codogno: quante cose ho dovuto ristudiare per scriverlo :-) ma spero di aver dato un’idea del come si può inviare messaggi con alta probabilità di ricezione.
- 21 – Le trasformazioni geometriche, di Bruno Cifra: una visione unificatrice di tutte le geometrie, seguendo il programma di Erlangen.
- 22 – L’algebra, di Paolo Gangemi: le definizioni di base dell’algebra come si studia all’università.
- 23 – I numeri complessi, di Marco Erba e Claudio Sutrini: molto interessante la parte dove si mostra come i numeri complessi siano necessari in fisica quantistica.
- 24 – L’analisi complessa, di Paolo Caressa: vincoli a gogo rendono più interessante la struttura rispetto all’analisi in campo reale.
- 25 – La teoria dei numeri, di Francesco Zerman: uno sguardo su alcune parti della regina della matematica, con parti che non trovate facilmente in giro come quella sui numeri p-adici.
- 26 – Le equazioni differenziali, di Marco Menale: dalla propagazione di un’epidemia a quella del calore, la parte della matematica che più serve alla fisica.
- 27 – La geometria algebrica, di Ottavio G. Rizzo: non arriviamo a risolvere l’Ultimo Teorema di Fermat, ma almeno abbiamo una minima idea del perché si parla di curve ellittiche.
- 28 – La teoria dei grafi, di Sonia Cannas e Ludovico Pernazza. Le basi di una teoria nata con Eulero e sviluppatasi soprattutto con i computer.
- 29 – L’analisi funzionale, di Pierluigi Vellucci: perché mai una funzione deve solo trasformare un numero in un altro numero, e non una funzione in un’altra funzione?
- 30 – La geometria differenziale, di Christian Casalvieri: dopo che l’analisi matematica ha sfruttato la geometria, ora le rende il favore.
- 31 – La matematica dei calendari, dei Rudi Mathematici: usare la matematica in maniera creativa per trovare una quadra dove non c’è.
Ci sono anche altre recensioni matematiche:
- Elogio delle matematiche, di Alain Baidou. Badiou la matematica la sa anche se è filosofo, Losito che l’ha tradotto un po’ meno.
- Dentro l’algoritmo, di Donata Columbro. Ho trovato molto meglio il suo precedente Ti spiego il dato.
- The Golden Ratio, di Mario Livio. Diciamo che ha fatto il possibile col materiale a disposizione.
- La sezione aurea, di Franco Purini: diciamo che non sono riuscito a capire dove si parlasse della sezione aurea.
- The Golden Ratio and Fibonacci Numbers, di Richard A. Dunlap: utile per vedere quali associazioni del rapporto aureo nell’arte sono essenzialmente delle bufale.
- Fibonacci Numbers and The Golden Ratio, tratto da un MOOC su Coursera di Jeffrey Robert Chasnov. Utile solo se non sapete nulla dell’argomento, ma con il vantaggio che il testo è liberamente scaricabile.
- Once Upon a Prime, di Sarah Hart: tante belle chiacchiere – spesso a me ignote – sulla matematica in letteratura.
- The Golden Ratio: The Facts and the Myths, di Francis D. Hauser. Molto minimale, probabilmente troppo.
- The Pleasures of pi, e, and Other Interesting Numbers, di Y. E. O. Adrian: tante formule di serie infinite per i ragazzi.
- Information Theory, Inference and Learning Algorithms, di David J. C. MacKay:come dice il titolo, un approccio non standard alla teoria dell’informazione.
Per quanto riguarda il mercoledì matematico:
- Quando la fattorizzazione non è unica: alcuni esempi di strutture in cui il teorema di fattorizzazione unica è falso.
- Una citazione inutile: alcune considerazioni non tanto sulla prova di matematica all’esame di maturità quanto sulle citazioni nel testo d’esame.
- Le elezioni legislative francesi: partendo dai risultati elettorali francesi (e inglesi) mostro come la matematica applicata al sistema di voto influenzi le scelte.
- Usare equamente una moneta iniqua: approfitto del post per mostrare due tipi completamente diversi di dimostrazione.
- Facile come 1+1: mostro come un sistema di intelligenza artificiale fa una somma modulare. Ufficio complicazione affari semplici.
- Non correte subito a estrapolare!: un esempio di come l’estrapolazione fatta senza pensare può essere peggiore di non dire nulla.
- Che cosa NON È una dimostrazione elegante: racconto quando (per me) una dimostrazione è brutta, anche se funzionante.
- E allora cos’è una dimostrazione elegante?: e poi il mio pensiero su cosa rende elegante una dimostrazione (conta anche l’imprevedibilità)
- Dadi non transitivi: Si possono costruire dei dadi A, B, C dove A in media vince su B, B su C e C su A.
- I dadi di Lake Wobegon: addirittura, si possono costruire dadi A, B, C dove in media ciascuno di essi ha un punteggio migliore della media degli altri due.
- Persi in una foresta: se sai la forma di una foresta ma non dove ti trovi né in che direzione guardi, qual è il percorso da fare per uscire il prima possibile nel caso peggiore?
- Il problema di Brocard: una delle tante congetture di teoria dei numeri che probabilmente non sarà mai dimostrata.
C’è una bella rassegna anche per i Quizzini della domenica:
- Senza conti: si può risolvere… senza conti.
- Quadrato ruotato: ha il bello che può essere risolto in vari modi.
- Multilingue: un’applicazione quasi completa della discesa infinita, con un salto mortale finale.
- Nove punti: chiama a gran voce il principio dei cassetti (e un po’ di geometria di base).
- Quadrante a zig zag: problemino puramente geometrico e pitagorico.
- Piramide numerica: è davvero facile, e la parte più interessante è trovare la soluzione più semplice.
- Batterie scariche: alla fine si è rivelato più complicato del previsto.
- Pesce: a prima vista è impossibile da risolvere, ma alla fine dà un risultato semplice.
- 13-14-15: si può risolvere con la legge dei coseni, ma c’è un sistema più divertente.
- Birra, e sai cosa bevi: abbastanza immediato da risolvere.
- Cioccolatini: per risolverlo ci vuole un po’ di pazienza.
- Tennis non transitivo: in un torneo all’italiana se tutti hanno vinto almeno una partita non c’è un ordine totale tra i giocatori.
Solo un paio di post per la serie povera matematica:
- Perché i maschi non allattano: come è possibile che riviste come Nature pubblichino certi articoli?
- Ognuno ha i suoi modelli: Un sedicente think tank liberale ha messo un post motivazionale: una frase di Unabomber.

È ora dell’altrettanto lunga lista di articoli di MaddMaths! e, come al solito, la parola passa a loro:
- C’è una nuova mini-serie a cura di Gabriele Belegni, dove esploreremo i concetti principali di una delle branche più affascinanti della matematica: la topologia. Cercheremo di scoprire le motivazioni e le idee che hanno spinto ad introdurre certi concetti concentrandoci sull’aspetto intuitivo piuttosto che su quello formale. Nella prima puntata scopriremo cosa studia la topologia partendo da due semplici triangoli. Trovate tutte le puntate su questa pagina.
- Una Intelligenza Artificiale fatta con 21 bicchierini Siete spaventati dall’intelligenza artificiale? Oppure ne siete entusiasti, ma non sapete bene perché? In questo articolo Massimo Ferri, topologo, matematico applicato, ci fa giocare con una versione molto semplificata di “macchina che impara”, mettendo insieme dei... bicchieri. Forse è il modo per capire meglio questa rivoluzione che già sta cambiando le nostre vite.
- Il senso del doppio È uscito il libro “Il senso del doppio – la matematica tra rebus e indovinelli” di Margherita Barile e Giuseppe Pontrelli. Vi proponiamo l’Introduzione del libro.
- Arriva Comunicamat 6 – online dal 9 all’11 ottobre 2024 La sesta edizione del congresso “Comunicare la matematica” ritorna con la stessa formula degli ultimi anni (online su canali dedicati) da mercoledì 9 a venerdì 11 ottobre 2024. Tre pomeriggi a distanza, dedicati a interventi sulla comunicazione e la divulgazione della matematica. Il congresso si può seguire anche come corso di aggiornamento, con iscrizione su SOFIA. Tutte le informazioni su programma, presentazione di ospiti e interventi, iscrizione, partecipazione si trovano sul sito https://comunicamat.unicam.it.
- Matematica e agrivoltaico Il 13 Febbraio di quest’anno è stato pubblicato sul sito del ministero il decreto che “promuove la realizzazione di sistemi agrivoltaici innovativi di natura sperimentale”. Il decreto mette a disposizione risorse per oltre un miliardo di euro con l’obiettivo di realizzare nuovi impianti per un totale di circa 1 GigaWatt (GW). Per comprendere l’entità della misura basti osservare che al 31 Dicembre 2022 la potenza totale installata era di 123 GW, mentre la potenza da fotovoltaico ammontava a 25 GW: si tratta quindi dell’1% circa della potenza totale, e del 4% di quella da fotovoltaico. Ma cosa sono questi “sistemi agrivoltaici”? E cosa c’entra la matematica? Scopriamolo insieme con questo contributo di Annalisa Pascarella dell’IAC-CNR e Alberto Sorrentino dell’Università di Genova, tra le persone fondatrici dello spin-off matematico BEES (bees.srl).
- Un’IA medaglia d’argento alle IMO2024? La notizia non arriva completamente a sorpresa: alcuni segnali, alcune anticipazioni erano nell’aria da alcuni mesi. Ma sapere che un’intelligenza artificiale è riuscita a risolvere correttamente 4 problemi dei 6 dell’ultima Olimpiade Internazionale di Matematica (IMO) fa comunque un certo effetto. Ce ne parla Luigi Amedeo Bianchi.
- Rivoluzioni matematiche: il teorema della palla pelosa di Silvia Benvenuti Con il numero di settembre de Le Scienze troverete in allegato (a 14,90 euro, il prezzo include la rivista) il ventiquattresimo dei trenta volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al teorema della “palla pelosa” ed è stato scritto da Silvia Benvenuti. Mentre, ad agosto è stato il turno dei Teoremi di Shannon a cura di Francesca Carfora.
- Archimede 2/2024: matematica e senso critico Vi proponiamo il sommario del direttore Roberto Natalini del numero 2/2024 della rivista Archimede:
Iniziamo questo secondo numero del 2024 di Archimede con un contributo importante di Anna Baccaglini-Frank, scritto con un gruppo di ricerca internazionale, sull’educazione matematica “tecnocritica”, un approccio che permette agli studenti di «impacchettare e spacchettare la matematica», sia riguardo l’uso della tecnologia digitale in classe sia riguardo l’esplorazione da parte degli studenti della tecnologia che li circonda. Segue la nuova puntata della serie promossa da Francesca Gregorio sui numeri nell’insegnamento con i numeri razionali. Infine Ruggero Pagnan ci propone alcune sfide matematiche che comportano l’esercizio del pensiero laterale. Per le Strane storie matematiche, proponiamo la discussione sul quesito Invalsi sui numeri pari e il lancio di una nuova storia. Il fumetto e la copertina, sempre dedicati a Mandelbrot, sono opera di Lorenzo Palloni, il titolo della storia è “Rugoso”.
- Abbiamo pubblicato un articolo di Daniele Gouthier contenente alcune riflessioni sulla comunicazione della matematica e il suo rapporto con la società. A questo sono seguiti gli interventi di Nicola Ciccoli e Domingo Paola. Si sono, poi, aggiunti Marco Menale con valorizzazione e università e Simone Ramello, dottorando all’ultimo anno presso l’Università di Münster, con il punto dall’estero.
- Risultati INVALSI 2024 in matematica: cosa ci possono dire (o non dire) i primi risultati L’11 luglio 2024 sono stati presentati i risultati delle prove nazionali INVALSI che, tra i mesi di marzo e maggio 2024, hanno coinvolto più due milioni e mezzo di studentesse e studenti italiani appartenenti alle classi II e V della scuola primaria, III della scuola secondaria di primo grado, II e ultimo anno della scuola secondaria di secondo grado. Le studentesse e gli studenti si sono cimentati in prove relative all’Italiano, alla Matematica e all’Inglese (Listening e Reading). Un primo commento di Ketty Savioli della Commissione Italiana per l’Insegnamento della Matematica (UMI-CIIM) sui risultati in matematica.
- Non solo applausi e medagliette – Giornata conclusiva del 31° Rally Matematico Transalpino a Firenze Il primo giugno 2024 si è tenuto a Firenze la 31° edizione del Rally Matematico Transalpino a Firenze. Pubblichiamo un appassionato reportage di un partecipato collettivo di organizzatrici e organizzatori: Brunella Brogi, Fabio Brunelli, Fabiana Ferri, Gianni Gallai, Mirko Marini, Silvia Mazzucco, Ginia Percario, Bice Perna, Chiara Pradella, Francesca Ricci, Valentina Scarpini.
Per La matematica danzante di Raffaella Mulas:
Per La Lente Matematica di Marco Menale:
- Probabilità: un pezzo della matematica ingiustamente bistrattato La probabilità può aiutare a comprendere i fenomeni del mondo nella loro complessità, così da evitare pregiudizi e false credenze. Quest’episodio è stato a quattro mani, tra superenalotto e test medici, con Angelo Vulpiani, Professore ordinario di Fisica Teorica alla Sapienza.
Non sarebbe Carnevale se non ci fossero i contributi dei Rudi Matematici ed ecco i “post istituzionali”:
- Chapeau! – Soluzione del quesito di giugno: c’era tutto un discorso parigino che riguardava la sottile capacità di individuare il colore del proprio cappello.
- Tappezzeria formato A8 – Soluzione del quesito di luglio: qui invece tutto il problema sta nello scrivere i numeri naturali tutti attaccati.
- La spiaggia delle meraviglie – Ad agosto, due problemi al prezzo di uno, con il Capo in vacanza che gioca a fare il Cappellaio Matto

I Q&D, invece, sono ben sette e il testo espositivo è così corto che non vale davvero la pena riassumerlo:
Oltre al post in tema Gianluigi Filippelli ha deciso di raccogliere tutti i post estivi in due post: il primo link raccoglie i contributi postati tra giugno e luglio, mentre il secondo raccoglie quelli postati tra luglio e agosto: ci sono le pubblicazioni su DropSea, quelle dal Cappellaio Matto e quelle in inglese, con alcune cose non necessariamente a tema matematico.
Tra gli articoli più recenti ci sono tre recensioni:
- Numeri visti di sbieco di Tommaso Maccacaro e Claudio Tartari
- Il teorema di Pitagora di Paolo Zellini
- Le equazioni differenziali di Marco Menale, 26.mo volume della collana Matematica curata dal “nostro” Maurizio Codogno
Nella sezione de Le grandi domande della vita, invece, ecco Di perimetri, aree e volumi sullo stretto legame analitico tra questi particolari “bordi” geometrici. Infine, dal Caffè del Cappellaio Matto, un post ne La scienza dei supereroi sulla ricorsione: L’Osservatore osserva l’Osservatore che osserva l’Osservatore...
In chiusura, non mi resta che presentare anche il mio articolo Non solo sport: nel quale elenco una serie di caratteristiche necessarie per una buona riuscita nello sport, riconoscendo come siano le stesse per la matematica. Per questo motivo, abbino allo sportivo nel quale ho riconosciuto questa caratteristica un matematico o un fisico, suggerendo letture e spunti di riflessione.
Questo è quanto…
Direi che la rassegna offre, come sempre, matematica per tutti i gusti. Ci si ritrova a ottobre!
Non solo sport
L’estate delle Olimpiadi porta con sé tantissime riflessioni. Personalmente, vivendo la scuola da insegnante di matematica, ho scoperto che matematica e sport hanno parecchio in comune: «Creare la matematica è un’esperienza sofferta e misteriosa» scrive Simon Singh e tutti noi sappiamo che realizzare le grandi imprese dello sport non è certo facile. Ho già tentato un’esplorazione di questi aspetti con le Olimpiadi di Tokyo, ma l’articolo che avevo scritto è stato pubblicato su un sito che ormai è chiuso e le mie riflessioni si sono perse nella nebbia del web. Provo a ripercorrere il sentiero di allora, aggiungendo nuove tappe e nuovi panorami, elencando le caratteristiche necessarie per una buona riuscita nello sport e abbinando ad ogni sportivo un matematico o un fisico, suggerendo letture e spunti di riflessione.
Forza di volontà
La forza di volontà è quella caratteristica che non si può che riconoscere a tutti gli atleti, ma se devo sceglierne un rappresentante propongo Gianmarco Tamberi, vincitore della medaglia d’oro nel salto in alto a Tokyo: sul gesso con il quale l’avevano fasciato dopo l’infortunio che gli era costato le Olimpiadi di Rio, nel momento in cui aveva deciso di ricominciare a lottare aveva riportato la frase “Road to Tokyo 2020” (poi corretto in 2021). Quel gesso l’ha accompagnato a Tokyo, come ricordo delle fatiche, fisiche e mentali, che aveva dovuto affrontare per raggiungere l’ambito traguardo, un «simbolo della mia forza d’animo, della mia volontà di provarci e riprovarci nonostante le avversità». La vittoria di Tamberi alle Olimpiadi di Tokyo è stata anche un esempio di amicizia, quella con Mutaz Essa Barshim, con il quale ha condiviso la medaglia d’oro. Abbiamo rivisto la stessa amicizia a Parigi, dove, però, la forza di volontà non è bastata: Gimbo ce l’ha messa davvero tutta per conquistare il podio anche in questa edizione, ma le sue condizioni di salute hanno remato contro di lui fin dall’inizio. Eppure, io credo che, nel fallimento dell’impresa, Gianmarco Tamberi abbia regalato a tutti noi più di quanto avrebbe potuto fare con una vittoria: ci ha dimostrato che, a volte, è necessario impegnarsi in tutti i modi, anche quando l’obiettivo sembra fuori dalla nostra portata. Dal canto suo, Gimbo aveva la consapevolezza di essere al meglio della forma e di poter dare buoni risultati, nel caso in cui fosse riuscito a combattere la sofferenza fisica.

La forza di volontà mi riporta alla mente tantissimi esempi e, tra tutti, scelgo quello di Marie Curie: il racconto della sua vita ci è presentato, in maniera essenziale, nella sua Autobiografia, dove non mancano riferimenti alla fatica di un lavoro ripetitivo, ma anche alla felicità che quel lavoro procurava a lei e a Pierre. «Una delle nostre gioie era recarci di notte nel laboratorio. Allora scorgevamo da tutte le parti le sagome debolmente illuminate dei flaconi e delle boccette che contenevano i nostri prodotti. Era davvero una vista incantevole e sempre nuova per noi. Le provette scintillanti sembravano tenui luci fiabesche.» Anche Marie Curie ha vissuto grandi amicizie nel corso della sua vita: oltre al sodalizio con Pierre, oltre all’amicizia con Albert Einstein, non si può dimenticare il patto stretto con la sorella Bronia, raccontato in Marie e Bronia, un patto tra sorelle. Bronia parte per Parigi per studiare medicina, mentre la sorella lavora come istitutrice per mantenerla agli studi; una volta conclusi gli studi di Bronia, anche Marie può partire per Parigi, potendo contare sul sostegno della sorella: il patto ha permesso a entrambe di realizzare il proprio sogno.
Nella vita di Marie Curie, non sono mancati i momenti di difficoltà: la morte di Pierre, quando le figlie erano ancora piccole, e poi l’attacco mediatico subito nel momento in cui è diventata di dominio pubblico la relazione con Paul Langevin. Sara Rattaro nel romanzo Io sono Marie Curie racconta molto bene questi momenti della vita di Marie Curie, immaginando che sia proprio lei a raccontare il dolore dopo la morte del marito, il ritrovato entusiasmo agli inizi della relazione con Langevin, e la forza di ricostruirsi, con l’appoggio degli amici, dopo i pesanti attacchi.
Determinazione
Un altro esempio di forza di volontà che non è riuscita a combattere la sfortuna ci è offerto da Derek Redmond, che alle Olimpiadi di Seoul del 1988 era stato obbligato a ritirarsi a causa di un infortunio, dieci minuti prima della gara. Quattro anni dopo, alle Olimpiadi di Barcellona, la sua voglia di vincere è al massimo livello: qualificatosi alle semifinali dei 400 m piani con il tempo migliore, sta affrontando al meglio la gara, ma dopo 250 m lo strappo del bicipite femorale destro lo obbliga a fermarsi, segnando la fine del suo sogno olimpico. Si rimette in piedi, perché vuole tagliare il traguardo: procede con determinazione, nonostante il dolore e, nella sua gara personale, lo raggiunge il padre, Jim, che lo sostiene fino alla fine, accogliendo le sue lacrime e cercando di consolarlo. Quando taglia il traguardo, Derek viene accolto dalla standing ovation dei 65 mila spettatori presenti. Il filmato della gara è disponibile sul canale YouTube ufficiale delle Olimpiadi, nella descrizione del quale si parla di «vero coraggio contro le avversità»: «Pochi ricordano che lo statunitense Steve Lewis ha vinto la semifinale in un tempo di 44.50. Ma nessuno, tra quelli che hanno visto la gara, può dimenticare il coraggio di Derek Redmond nel giorno che ha definito l’essenza dello spirito umano e olimpico».
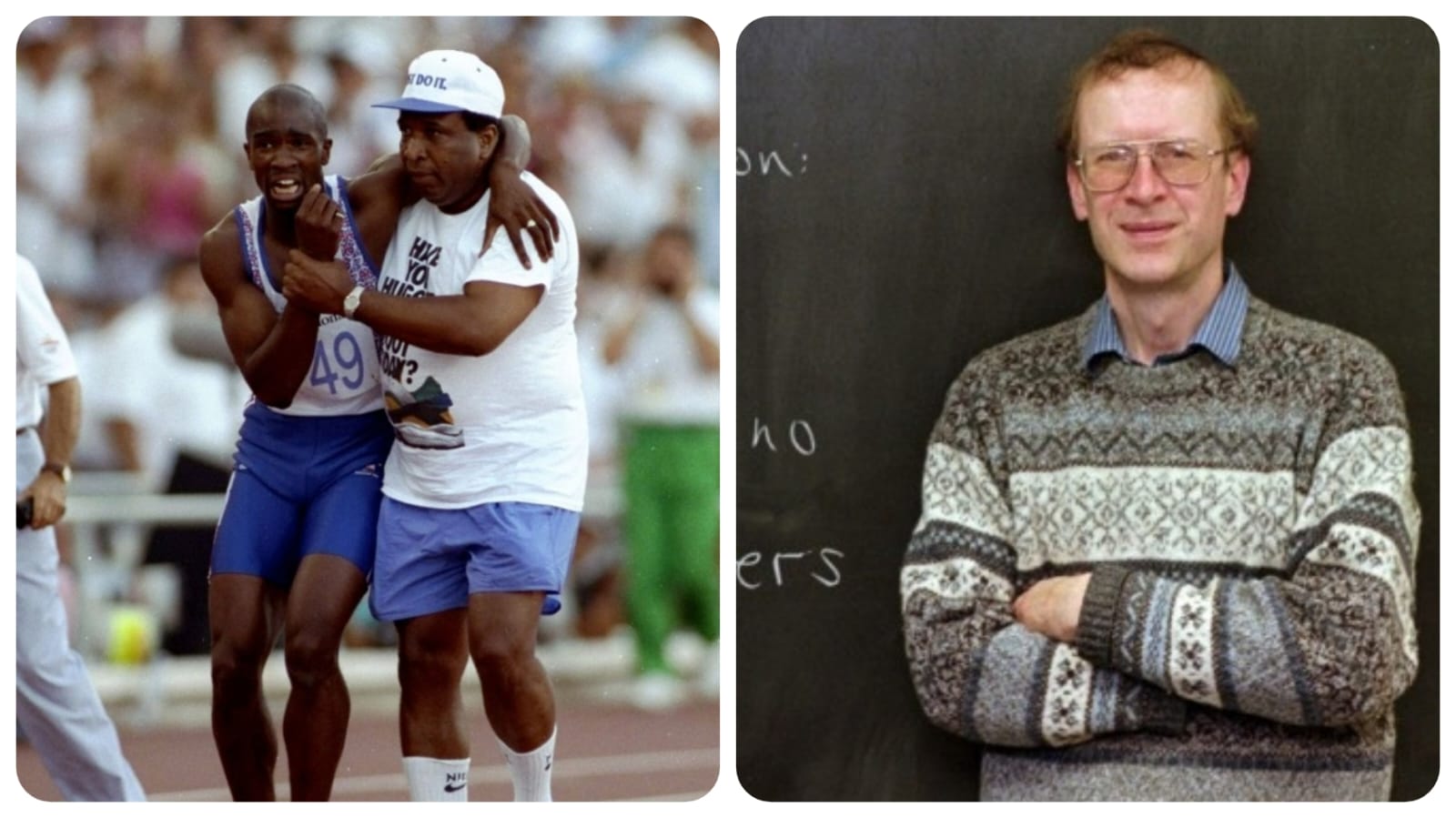
«Da quando l’ho incontrato per la prima volta da bambino, l’Ultimo Teorema di Fermat è stata la mia grande passione»: sono le parole di Andrew Wiles riportate da Simon Singh nel celebre L’Ultimo teorema di Fermat, il racconto di una dimostrazione che ha richiesto più di 350 anni. La passione per una delle congetture più celebri, e forse più semplice da enunciare, della storia della matematica accompagna Wiles nella sua crescita e, quando decide di impegnarsi seriamente nella dimostrazione, lavora in completo isolamento e in segreto, quasi ad imitare il lavoro di Fermat: «Capii che tutto ciò che ha a che fare con l’Ultimo Teorema di Fermat genera un interesse eccessivo. Non è possibile rimanere concentrati per anni a meno che non ci sia un completo raccoglimento, che troppi spettatori avrebbero distrutto.» Forse non c’è stata una standing ovation quando Andrew Wiles ha concluso la sua conferenza, nel giugno del 1993, dicendo: «Penso di fermarmi qui», ma c’è stato un lungo applauso, dopo che un silenzio denso di attenzione e solennità aveva accolto la sua dimostrazione. Quel momento di gloria sembra rovinato dalla scoperta di un errore: «A meno di sei mesi dalla conferenza al Newton Institute, il sogno d’infanzia di Wiles era a brandelli. Alla gioia, alla passione e alla speranza che lo avevano accompagnato negli anni trascorsi a eseguire calcoli in segreto si sostituirono l’imbarazzo e la disperazione.» Credo che sia proprio in questo momento che viene allo scoperto la determinazione di Wiles: non sono bastati gli anni in solitudine a lavorare alla dimostrazione, è in questo momento che la sua forza si mostra in tutta la sua bellezza, adesso che gli occhi della comunità matematica sono puntati su di lui e che qualcuno comincia a parlare di fallimento dell’impresa. «Dopo essere stato spinto sull’orlo della resa, Wiles aveva reagito dimostrando il proprio genio al mondo. Gli ultimi quattordici mesi avevano rappresentato il periodo più doloroso, umiliante e deprimente della sua carriera matematica. Adesso un’intuizione brillante aveva posto fine alla sua sofferenza.» Difficile riuscire a raccontare meglio di Singh questa impresa eccezionale.
Grinta
Come Tamberi, anche Bebe Vio ha puntato alle Olimpiadi di Tokyo accompagnata da un conto alla rovescia: ha parlato dei suoi 119 giorni, quelli che ha dedicato alla preparazione per le Paralimpiadi, «119 giorni per raggiungere l’impossibile» (come ha titolato Repubblica): anche lei, durante la gara, aveva con sé il braccialetto dell’ospedale sul quale era scritto «– 119» e solo a gara conclusa abbiamo saputo del terribile verdetto di aprile e dei rischi corsi a causa di un’infezione. In realtà, anche questa competizione è stata preceduta da molte difficoltà: sono passati solo tre anni da Tokyo e Bebe Vio ne ha usati due per sottoporsi a interventi chirurgici per essere al meglio della forma. Con la positività che la contraddistingue è riuscita a dire: «è stato un periodo difficile, ma è stato fantastico» e questo perché ha avuto il supporto di varie figure che l’hanno aiutata a coronare il sogno di ottenere la medaglia di bronzo sia nel fioretto individuale che in quello a squadre.
Prima ancora della competizione, Bebe Vio aveva dichiarato sui social che non avrebbe partecipato alle Paralimpiadi di Parigi, ma che avrebbe GAREGGIATO, facendosi portavoce di un cambiamento non solo verbale, ma di sostanza, culturale. Possiamo ricordare le sue parole, citate in questo articolo di Lorena Encabo e Benedetto Giardino: «Sappiamo di avere il potere di provare a dire qualcosa. Sappiamo che ogni punto qui, alle Paralimpiadi, potrebbe essere un punto con cui possiamo smuovere le persone, se un piccolo ragazzo con una disabilità sta guardando la televisione in quel momento specifico, guardando quel singolo punto. Possiamo letteralmente scuoterle e dire loro: “Ok, lo sport è bello, è sano, è fantastico”. È qualcosa di così bello e vogliamo che quante più persone possibili si spingano un po’ di più.»

Anche Cedric Villani, come Bebe Vio, dopo aver identificato il suo obiettivo, ha dovuto confrontarsi con un conto alla rovescia serrato: «Dopo mi resteranno cinque mesi, li passerò sul mio grande sogno, la regolarità di Boltzmann! A questo fine mi sono portato dietro degli appunti che ho scribacchiato in una decina di Paesi differenti.» Il sogno di Villani è l’Olimpo della matematica, la medaglia Fields, ma il conto alla rovescia è necessario: «Il limite di età a 40 anni, che stress! Non ho che 35 anni… […] Nel 2014 per soli 3 mesi sarò troppo vecchio; la MF sarà quindi nel 2010 o mai più.» Il teorema vivente è il racconto di questa impresa: narrato in prima persona, ricco di storia della matematica, di fumetti e di matematica, è un libro da leggere e da far leggere, per poter capire cosa significhi fare matematica ad alto livello. «Non ha prezzo un sentiero senza illuminazione! Quando non c’è la luna, non si ha neanche una visibilità di tre metri. Il passo accelera, il cuore batte un po’ più in fretta, i sensi restano sul chi vive. Uno scricchiolio nei boschi fa drizzare le orecchie, ci si dice che la strada è più lunga del solito, ci si immagina un malintenzionato in agguato, ci si trattiene a malapena dal mettersi a correre. Questa galleria buia è un po’ come la fase buia che caratterizza l’inizio di un progetto matematico», ma in fondo è così l’inizio di qualsiasi progetto.
L’importanza della squadra
Nel suo avvicinamento al traguardo, Derek è stato sostenuto dal padre Jim, la sua squadra. Ripensare alle olimpiadi del 2021 non può che riportarci alla mente la squadra italiana che ha vinto la medaglia d’oro nella staffetta maschile 4x100 m: Patta, Jacobs, Desalu e Tortu. Domenico Licchelli, astrofisico che si occupa di didattica e comunicazione scientifica, ha evidenziato, in un post su Facebook, gli aspetti matematici e fisici che si nascondono dietro la vittoria della staffetta: i corridori devono avere, innanzi tutto, caratteristiche diverse, visto che «il primo frazionista deve essere un buon partente ed un buon corridore in curva. Il secondo frazionista deve essere potente nella corsa lanciata e resistente a lungo ad alta velocità. Il terzo deve esprimere una potenza muscolare tale che gli consenta di sopportare le maggiori spinte in curva opponendosi alla gravità terrestre ed alla forza centrifuga. […] Il quarto dovrà eccellere nella corsa lanciata e saper gestire le forze per portare a termine l'impresa, mantenendo il vantaggio o recuperando terreno». E tutto questo ancora non basta per vincere, perché conta anche l’«indice di cambio», ovvero la capacità di scambiarsi il testimone nel più breve tempo possibile e, per rendere l’operazione il più fluida e veloce possibile, è necessario provare e riprovare. Non possiamo riassumere il tutto dicendo semplicemente che l’unione fa la forza, perché è necessario ricordare anche l’esercizio che migliora le prestazioni. Nella vita scolastica, entrambi gli aspetti sono importanti, innanzi tutto perché i ragazzi si trovano inseriti in due squadre, la squadra formata dalla classe – perché a scuola non si impara come singoli ma come gruppo – e la squadra formata con i propri docenti, preparatori atletici consapevoli di ciò che è necessario fare per affrontare al meglio il percorso, e in secondo luogo perché è necessario un continuo esercizio per migliorare le proprie prestazioni (e non solo in matematica).

La squadra è presente nel lavoro di Cedric Villani: «Quello che anzitutto apprezzo del mio laboratorio, così piccolo e insieme così dinamico, è il modo in cui gli argomenti si mescolano tra i ricercatori di diversi orizzonti matematici, davanti alla macchina del caffè o nei corridoi, senza timore delle barriere tematiche.» La squadra è quella che ha formato Maryam Mirzakhani prima con Curtis McMullen e poi con Alex Eskin, dell’Università di Chicago, come raccontato in questo video. Ma se penso ad un’altra squadra, mi viene in mente, in tempi recentissimi, quella mostrata nel video dell’Università di Parma, realizzato in occasione dell’assegnazione dell’EMS Prize a Cristiana De Filippis: la giovane matematica parla di come sia stata attirata a Parma, durante il suo dottorato a Oxford, per la ricerca di alto livello fatta dal gruppo di analisi, racconta del suo lavoro dai ritmi intensi e senza orari, racconta con passione ed entusiasmo come si approccia alla ricerca. E poi ci sono le parole di Tuomo Kuusi dell’Università di Helsinki e di Giuseppe Mingione dell’Università di Parma con i quali sta lavorando. Il video ci permette di cogliere il senso di una squadra, di vedere le risate e la complicità che legano i singoli componenti.
Gli errori
Nello sport come nella vita non mancano gli errori e i fallimenti: cominciamo da una (rara) sconfitta di Sinner ai primi di luglio di quest’anno e dal commento di Panatta al riguardo: «Nel tennis si perde, i più forti non lo fanno così spesso, e Jannik Sinner è tra questi, ma ogni tanto succede anche a loro. Esiste una normalità della sconfitta che andrebbe maggiormente rispettata.»
Il secondo fallimento (perché qui non si tratta di errore) è quello di Ambra Sabatini alle Paralimpiadi di Parigi: la sua emozionante intervista dopo la gara, e dopo la caduta che le è costata il podio, mostra tutta la sua grandezza, visto che parla del suo senso di colpa per aver rovinato la gara di Monica Contrafatto, ma mostra anche la sua grinta quando dice «Ho superato tante cose, supererò anche questa». Lo sguardo di Ambra è già puntato avanti: «C’è dell’amaro ora, so che però ho tante opportunità davanti ed è già cominciato il percorso verso Los Angeles 2028», perché, come diceva Paola Egonu all’indomani delle Olimpiadi di Tokyo, gli errori sono importanti per migliorarsi e crescere.
Di errori ha parlato anche Julio Velasco, all’indomani della vittoria della medaglia d’oro: intervistato dai giornalisti che gli hanno chiesto se avesse ritrovato la pace dopo le Olimpiadi di Atlanta del 1996, dove la nazionale maschile da lui guidata aveva perso in finale contro l’Olanda, il celebre allenatore ha parlato con la consueta saggezza ricordando che nello sport funziona così, a volte si perde per un soffio e a volte si vince per un altro soffio. La sua grandezza è nell’aver accettato la sconfitta che forse molti tifosi ancora non hanno accettato, ma soprattutto nel non accettare di essere messo su un piedistallo dopo la vittoria alle Olimpiadi: «Non siamo speciali. Siamo vincenti. In questa occasione siamo stati i vincitori.» Se si accettasse di essere speciali quando si vince, bisognerebbe mettere in conto di non esserlo quando si perde, e Velasco non si lascia vincere da questa tentazione.

Nel cercare storie per questo articolo, nel libro di Simon Singh sull’ultimo teorema di Fermat ho trovato due riferimenti al ruolo di Eulero nella costruzione della dimostrazione: «Il matematico più creativo della storia fu umiliato dalla sfida di Fermat», scrive inizialmente Singh. Ma, subito dopo, scrive qualcosa di ancora più grande: «Per nulla scoraggiato dal fallimento, Euler continuò a creare geniali teorie matematiche fino alla morte, un risultato reso ancor più notevole dal fatto che durante la fase conclusiva della sua carriera rimase completamente cieco.» Come non citare, infine, Alessio Figalli? In un’intervista con l’Università di Padova nel marzo di due anni fa, ha parlato proprio dell’errore: «Vivo nel fallimento, come tutti gli scienziati. Diciamo che per un problema risolto, dieci non riesco a risolverli. […] La ricerca è fatta di fallimenti e non c’è niente di male. Ognuno di noi, quando fa ricerca, deve capire come gestire la frustrazione del fallimento, perché quella è inevitabile: io, per esempio, la gestisco lavorando su più problemi. Di solito magari da due o tre non riesco a tirare fuori nulla, però magari al quarto che sto facendo qualcosa salta fuori e quello mi dà la motivazione e la soddisfazione per gestire poi quelli che non funzionano.»
La medaglia di legno
Tendiamo a considerare il quarto posto, quando il podio ti sfugge per poco, il fallimento peggiore, eppure dal 3 agosto potremmo avere una visione diversa della cosa. In quella data, Benedetta Pilato si è classificata quarta, a un solo centesimo dal podio, nei 100 m rana: l’abbiamo sempre raccontata così, che ha perso il podio per un centesimo, ma da subito dopo la gara, durante un’intervista, la nuotatrice ci racconta una realtà diversa, cambiando il nostro punto di vista al riguardo, parlando del giorno più felice della sua vita. Ma come è possibile? «Questo è solo un punto di partenza» dice e poi ricorda: «Un anno fa questa gara non ero nemmeno in grado di farla.» La bellissima testimonianza di Benedetta Pilato e la polemica che ne è seguita – e che ha contribuito ad attirare l’attenzione sul problema – hanno permesso di cominciare a cambiare il punto di vista, tanto che, nella cerimonia del Quirinale che si svolgerà a fine mese, Mattarella riceverà anche i classificati al quarto posto.
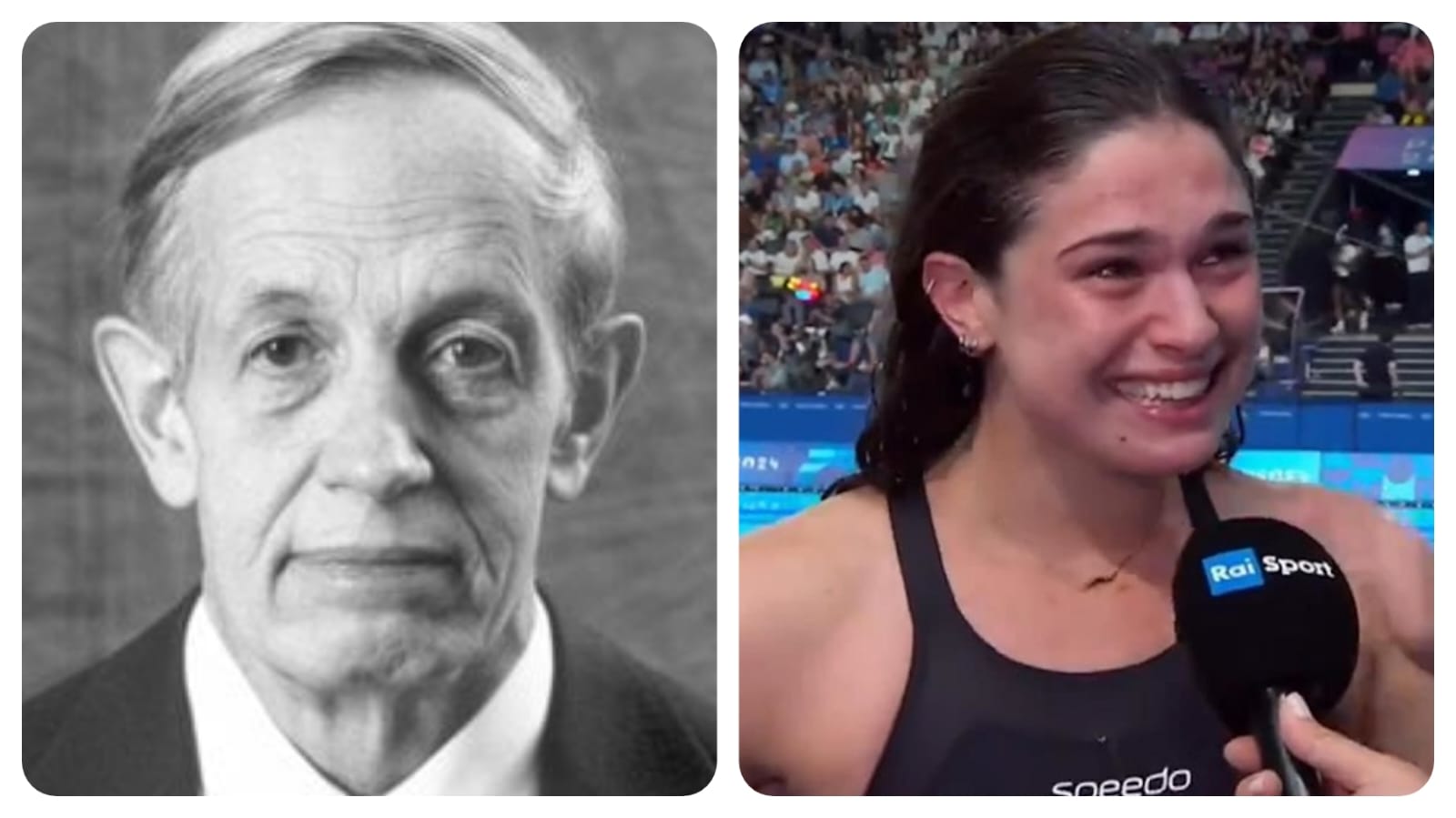
C’è un illustre esempio anche nella matematica di una medaglia mancata, ed è realmente una medaglia, trattandosi della prestigiosa Fields: nel 1957, sia Ennio De Giorgi che John Nash “incontrano” il diciannovesimo problema di Hilbert, uno dei 23 proposti dal matematico tedesco durante la conferenza del Congresso Internazionale dei matematici a Parigi nel 1900. De Giorgi lo dimostra con metodi mai usati in precedenza e pubblica la soluzione su una rivista italiana non molto nota all’estero, mentre John Nash arriva alla soluzione un paio di mesi dopo. «Quarant’anni più tardi, dopo aver vinto il Nobel, Nash accennò a quelle speranze infrante nel suo saggio autobiografico, esprimendosi nel suo abituale stile ellittico: “Sembra plausibile che, se De Giorgi o Nash non avessero risolto questo problema (o i calcoli aprioristici sulla continuità effettuati da Holder), l’unico scalatore a raggiungere la vetta sarebbe stato il vincitore della Fields (che di solito viene conferita a persone con meno di quarant’anni).”» La delusione di Nash fu grandissima, come viene ben descritto nel libro appena citato di Sylvia Nasar Il genio dei numeri.
Il talento
«Effortless is a myth», ovvero: il fatto che un obbiettivo possa essere raggiunto senza sforzo è un mito, dichiara Roger Federer nel suo celebre discorso all’Università di Dartmouth, proponendo questa affermazione come prima lezione (sono tre in totale).
Gregorio Paltrinieri ha dichiarato durante le Olimpiadi: «Non sono qui grazie al talento, sono qui grazie al sacrificio che faccio tutti i giorni» dopo le due medaglie vinte a Parigi.
«Sveglia alle sei e mezza, alle 7 e mezza già in piscina, tre ore di allenamento, cinque chilometri di nuoto, sonnellino, pranzo, poi di nuovo piscina, altri cinque chilometri, cena alle 20 e a letto presto.» è la vita che dichiara di aver condotto Thomas Ceccon per prepararsi alle gare.

Ecco un altro dei terribili miti che vanno assolutamente sfatati: parlare di talento nasconde la volontà di crearsi un alibi. Se riconosco “solo” il talento a Federer, a Paltrinieri, a Ceccon, nessuno pretenderà da me che io mi impegni per raggiungere simili obiettivi; se, invece, riconoscessi il lavoro e lo sforzo fatto, mi renderei conto che potrei raggiungere anch’io obiettivi di un certo livello. Questo non vale non solo nello sport, ma ovunque: «La verità è che ho dovuto lavorare molto duramente per farlo sembrare facile» dichiara Federer.
Non posso non citare le parole di Katalin Karikò, dalla sua autobiografia, Nonostante tutto:
«Non mi considero particolarmente intelligente. Nel corso degli anni ho conosciuto molte persone apparentemente dotate di una memoria fotografica che permetteva loro di imparare senza fatica. A uno dei miei compagni di scuola delle elementari bastava sentir dire una cosa una volta e non se la scordava più. Io no, non ho mai avuto questo dono. Ma già da piccola avevo capito una cosa fondamentale: quello che mi mancava a livello di abilità naturali, potevo compensarlo con lo sforzo. Potevo impegnarmi di più, applicarmi per un numero maggiore di ore, fare di più e farlo con maggiore attenzione.
Persino in prima elementare e in seconda elementare mi impegnavo con tutta me stessa nello studio. Cercavo di non sbagliare niente. Se commettevo un errore, ricominciavo da capo.
Studiavo.
Studiavo.
Studiavo.
E, coincidenza, a quanto pare il cervello è malleabile. Più lo esercitiamo, più lo rafforziamo. Quanto a me, mi sono esercitata a eccellere negli studi: era un esercizio attivo, come allenarsi a fare canestro per un aspirante atleta. Come un atleta, miglioravo. Man mano, per me la scuola è diventata un ambiente sempre più naturale. In terza elementare ero talmente immersa negli studi che ho iniziato a prendere sempre 5 [il massimo dei voti], e non ho più smesso.
Né, aggiungerei, ho mai smesso di esercitarmi.»
Come già fatto in Inesauribile caparbietà, non posso non citare Gigliola Staffilani, prima donna italiana full professor al MIT, che alla domanda di Roberto Natalini in un’intervista del 2018 «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?» ha dato una bella risposta: «Credo che l’intuizione arrivi quando ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte.»
Infine, a tutti coloro che parlano di talento matematico non posso che suggerire la lettura del libro di Stanislas Dehaene Il pallino della matematica.
Lo sport ci insegna che non sempre è possibile realizzare i propri sogni e così, a scuola, quel 10 che sentivamo di meritare davvero a volte ci viene negato, ma questo non è necessariamente una cosa negativa. Ciò che conta è imparare, e ricordiamo le parole di Einstein, scritte nel 1931 in «Come io vedo il mondo»: «È nella crisi che sorge l’inventiva, le scoperte e le grandi strategie».
Matematica estiva
Alla ricerca di ispirazione per il Carnevale della Matematica, con il tema “matematica estiva” lanciato da Maurizio Codogno, faccio scorrere le foto della scorsa estate e realizzo che le foto di prati verdi e boschi rigogliosi che costellano in genere le mie estati (sono un’appassionata di camminate in montagna) si alternano a foto di bottiglie di Klein colorate realizzate all’uncinetto, di pantaloni molto ampi e altre amenità legate alla topologia. Dal 2016 ad oggi, le mie estati sono state arricchite dalla preparazione dei laboratori per il Festival di BergamoScienza, che si tiene ad ottobre, e, quindi, so che anche quest’anno la mia matematica estiva sarà ricca di prospettiva, visto che il mio cellulare già esplode di fotografie inerenti disegni prospettici, illusioni ottiche, anamorfosi, carte geografiche e tanto altro.
Vorrei concentrarmi, però, in questo caso, sulla matematica in montagna: il mio occhio ormai allenato (ossessionato, direbbe qualcuno) è abituato a individuare la matematica ovunque, e, mentre sono impegnata a raggiungere la meta del giorno, la mente vaga e cerca la matematica nella natura.

Comincio con gli straordinari giochi di luce che sul finire dell’estate interessano le due montagne (sacre, per gli antichi Camuni) che si fronteggiano nella Media Valle Camonica, il Pizzo Badile, protagonista al mattino, e la Concarena, che si ammanta di luce al tramonto. I raggi di luce, che all’Equinozio proiettano l’ombra delle montagne nel cielo, si mostrano come semirette con un’origine comune.

Quando si cammina in montagna, uno dei problemi con i quali ci si confronta di più è quello della pendenza: sono in bilico tra una terza e una quarta liceo scientifico e realizzo che quella che abbiamo visto fino a questo momento come pendenza della retta (ed esplorato in lungo e in largo anche con la cinematica e i diagrammi dei moti unidimensionali), ora diventerà la tangente dell’angolo formato dalla retta con l’asse delle ascisse, visto che cominceremo ad aggirarci tra i meandri della goniometria. La pendenza ha un ruolo determinante nella scelta di una camminata in montagna, perché non conta solo il dislivello che si deve colmare per raggiungere la meta, ma anche lo sviluppo del percorso. Diciamo che la pendenza è forse l’aspetto matematico più bistrattato durante le camminate di gruppo: il tratto che per chi ha allenamento e abitudine alla fatica è in genere un falso-piano, per chi è affaticato diventa una salita ripidissima.
«… chi va in montagna mi capisce al volo: una di quelle volte che ti sei alzato la mattina presto, stai sudando ormai da ore come un becco, sotto lo zaino, verso il rifugio che è là… son tre ore che è là… perché li spostano! Ci ho messo anni a capirlo: lo fanno per il tuo bene ma li spostano, chiaro!» [dal monologo teatrale di Marco Paolini Il racconto del Vajont]
Camminare in montagna aiuta a mettere le cose in prospettiva, per questo l’attività ha degli innegabili benefici psicologici, ma fa anche vedere le cose da un’altra prospettiva: «Tu sei là che ti domandi chi è che te l’ha fatta fare tutta ‘sta fatica, ti casca l’occhio indietro un attimo, e capisci da solo che valeva la pena di fare tutta la fatica del mondo per arrivare là, in quel momento li, perché giù, il fondo valle da dove sei partito, è già coperto di nuvole, ma tu ormai sei sopra. È limpido sopra. A trecentosessanta gradi hai le montagne, le crode, (…) che ti par di poterci volar sopra come un rapace» [Marco Paolini] Infine, la prospettiva cambia la nostra percezione delle altezze:

La seconda foto è stata scattata dal fondo valle, mentre la prima è stata scattata dal Bivacco Adamone, che si trova a un’altitudine di 1456 m. La percezione che si ha dal fondo valle delle altitudini è ben diversa dalla realtà: il Pizzo Badile ha un’altitudine di 2435 m, mentre la conca del Tredenus che lo circonda possiede parecchie cime, tutte più alte, ad esempio: Cima del Dosso (2785 m), Cima Meridionale (2796 m), Corno delle Pile (2805 m). Ecco spiegati gli inganni della prospettiva e, forse, anche il motivo per cui tendiamo a stimare la meta più vicina di quanto non sia.

Lungo il cammino, fra la vegetazione possiamo riconoscere delle felci: costituiscono un ottimo esempio di frattali, dei quali prima di BergamoScienza 2018 e della costruzione del grande triangolo di Sierpinski avevo un’idea molto vaga. Secondo la definizione di Wikipedia, «un frattale è un oggetto geometrico dotato di omotetia interna: si ripete nella sua forma allo stesso modo su scale diverse, e dunque ingrandendo una qualunque sua parte si ottiene una figura simile all’originale». Infatti, anche se concentriamo la nostra attenzione su un piccolo rametto di felce, questo potrebbe essere, nella giusta scala, la felce più grande dalla quale è stato preso.

Se abbiamo la fortuna di andare in montagna dopo una nottata di pioggia, oltre a poter apprezzare maggiormente il panorama, che è più limpido, potremmo anche imbatterci in una lumaca che attraversa il sentiero. Ma la spirale sul suo guscio è logaritmica o archimedea? La spirale archimedea mantiene costante la distanza tra due spire successive, mentre per la logaritmica questa distanza cresce secondo una progressione geometrica. Mi sono portata a casa la domanda e ho cercato, nei giorni successivi, una risposta. L’ho trovata nel blog Base 5 di Gianfranco Bo, il quale ipotizza anche una risposta sul motivo per cui la spirale della chiocciola sia logaritmica: la chiave potrebbe essere nella necessità del mantenimento della forma durante la crescita, ma per un approfondimento non resta che dare un’occhiata al suo lavoro.

Ritroviamo il lavoro di Gianfranco Bo anche nel post I fiori di Fibonacci del blog Sanoma. In effetti, ammirare i fiori, in montagna o altrove, rimanda sempre alla successione di Fibonacci, la sequenza di numeri che comincia con la coppia di 1 e prosegue autogenerandosi: il terzo numero è la somma dei primi due (2) e così ogni numero è la somma dei due che lo precedono, facendoci ottenere 1 1 2 3 5 8 13 21 34 55 89… Nel mio collage di foto compare del Semprevivo dei tetti, esempio matematico classico come possiamo vedere in questa mostra fotografica organizzata dall’Università di Pisa, il fiore del Ginepro, la minuartia austriaca, per me ottimo esempio di pentagono regolare, la genzianella primaverile, che spicca per il suo colore, la primula comune, che possiamo trovare anche senza bisogno di salire ad alta quota, il papavero alpino retico, la macchia di colore che spunta tra le rocce, e infine la mitica stella alpina.

Se durante la camminata raggiungiamo un laghetto, come nel caso del Lago Smeraldo in Val di Non o del lago d’Aviolo in Valle Camonica, si può osservare la simmetria assiale all’opera. La bellezza, in questo caso, è duplicata, grazie all’armonia delle forme e ai colori, che ci restituiscono il sapore di un lago incontaminato.

Anche i corsi d’acqua regalano grandi soddisfazioni matematiche: ogni volta che mi affaccio sulla Valle Adamé e vedo il serpeggiare del torrente Poia, che di anno in anno scava sempre di più il suo percorso creando nuove anse, non posso che ricordare la presenza nascosta del pi greco. Il matematico Hans-Henrik Stolum, in un lavoro pubblicato su Science nel 1996, ha mostrato che se si divide la lunghezza effettiva di un fiume, dalla sorgente alla foce, per la sua lunghezza in linea d’aria, si ottiene, approssimativamente, pi greco. Sul sito Matematica Russell, curato dal dipartimento di matematica e fisica dell’omonimo liceo di Roma in collaborazione con gli studenti, troviamo una precisazione: «Questo rapporto, però, non è una legge, infatti il rapporto di pi greco si trova più comunemente in quei fiumi che scorrono attraverso pianure che hanno un dislivello molto tenue.» Il torrente Poia ha, appunto, le caratteristiche necessarie.

Il penultimo tassello di questa camminata in montagna rimanda alle tassellazioni (che per quanto mi riguarda assocerò sempre alla prima esperienza con i laboratori di BergamoScienza): questo ultimo tratto del sentiero che porta al Lago della Vacca, realizzato con il granito dell’Adamello, ricorda in qualche modo una tassellazione. È un tratto pianeggiante, durante il quale si può ammirare il panorama, senza essere sovrastati dalla fatica.

L’ultimo passo, però, è quello più goloso: ormai raggiunta la meta, si può accedere al Rifugio, per riposare, riscaldarsi con un bel tè caldo e mangiare una fetta di torta. La mente, ormai allenata a trovare la matematica ovunque, non può che ritrovare la scodella di Galileo tra le tipiche scodelle dei rifugi, e chiedere di avere un settore circolare abbastanza ampio, quando sceglie la torta che preferisce.
Carnevale della matematica #178
“Canta, monello”
(poesia gaussiana)
Benvenuti all’edizione numero 178 del Carnevale della matematica!
Come i precedenti, il numero 178 è introdotto dalla consueta CELLULA MELODICA predisposta da Flavio Ubaldini, in arte Dioniso, che l’ha introdotta in questo modo: «Ecco anche la cellula melodica caratterizzata da un impegnativissimo intervallo di quattordicesima maggiore. Pare che il nostro soprano si stia stancando. Dice che vuole essere sostituita da un basso. Vedremo come accontentarla.»
Nonostante la pagina di Wikipedia sia un po’ scarna, al riguardo, devo dire che ricordare le proprietà dei numeri svela sempre qualcosa di interessante. Per cominciare, 178 ha come fattori 2 e 89 – come si vede anche nella cellula – che sono primi di un certo rilievo: 2 è l’unico numero primo pari, oltre ad essere il primo numero primo, e 89 è undicesimo nella successione di Fibonacci ed è un numero primo di Germain, ovvero tale che 2x89+1 sia primo (e infatti il prossimo Carnevale della matematica – spoiler! – sarà primo). Dato che è prodotto di soli due fattori primi, 178 si definisce semiprimo e, come tale, è utile in crittografia, ma è anche omirpimes, ovvero semiprimo non palindromo, anche se è ancora semiprimo quando scritto con le cifre in ordine inverso (871=13x67).
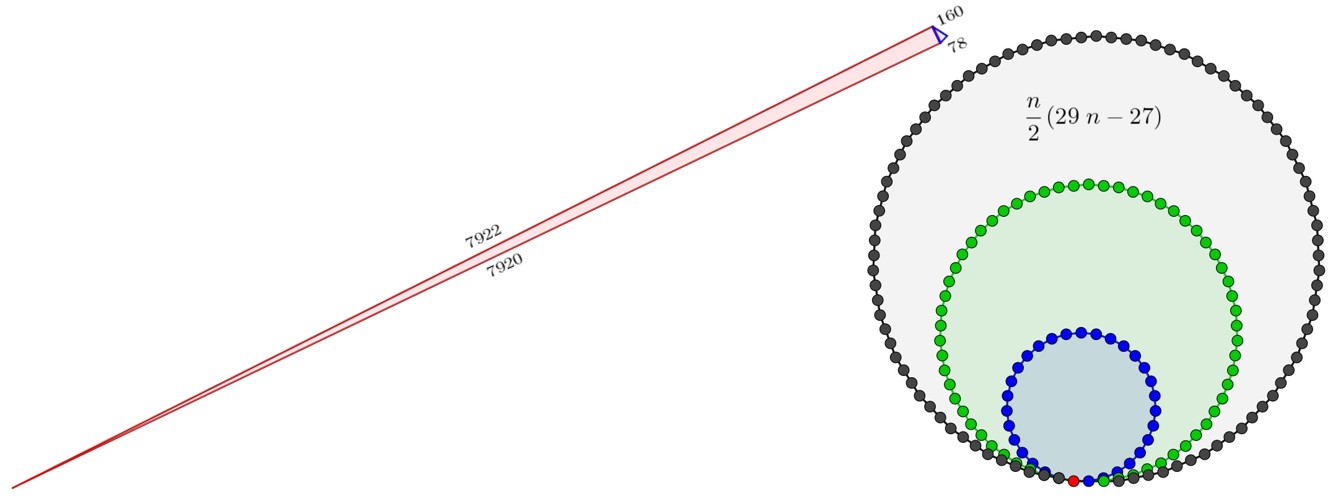
È un numero difettivo, in quanto maggiore della somma dei suoi divisori propri (89 e 2 in questo caso), è il quarto numero 31-gonale, la cui rappresentazione ricorda delle collane di perle e la cui formula ho trovato nel sito MathJoker. 178 è anche cateto minore o ipotenusa in due triangoli rettangoli che, rappresentati, danno una situazione un po’… spinosa!
Il tema di questo 178° Carnevale non poteva che essere “Donne e matematica”: infatti, mentre il Carnevale viene pubblicato il 14 del mese, la scadenza per l’invio dei propri contributi è il 12 e il 12 maggio è, dal 2019, la Giornata Internazionale delle Donne nella Matematica. Grazie a Maryam Mirzakhani, la matematica ha una Festa delle Donne tutta speciale: Maryam è nata il 12 maggio 1977 ed è stata la prima donna ad essere insignita della Medaglia Fields. Dopo la sua morte, avvenuta nel 2017 per un cancro al seno, il 31 luglio 2018, durante il World Meeting for Women in Mathematics, si è deciso di ricordarla con una festa speciale. Come spesso succede in matematica, le giornate speciali offrono un’occasione unica alla divulgazione ed è per questo che sono numerosi gli eventi previsti proprio in questi giorni di maggio. Il sito MaddMaths! offre un elenco dettagliato degli eventi italiani: al momento della pubblicazione gli eventi di Napoli, Torino, Roma, Pisa, Padova, Concesio (Bs), Brescia, Camerino e Roma hanno già avuto luogo, ma mancano all’appello quelli del 15 (a Firenze e a Reggio Emilia), quello del 16 a Roma e i laboratori de L’Aquila, che termineranno il 17 maggio.
Per quanto riguarda il Carnevale, il tema offre l’opportunità di presentare una rassegna di matematiche di tutto rispetto.
Cominciamo con un articolo di Annalisa Santi per il blog Matetango: Chi ha paura di Cecilia Payne? Matematica e astronoma britannica, nata il 10 maggio 1900, è stata vittima di sessismo nella scienza. La sua passione per l’astronomia nasce dopo aver assistito a una conferenza di Arthur Eddington, ma per poterla coltivare deve lasciare l’Inghilterra, nel 1923, grazie a una borsa di studio femminile dell’Osservatorio di Harvard. Fu così che «nel 1925 divenne la prima persona a conseguire un dottorato di ricerca in astronomia presso il Radcliffe College dell’Università di Harvard». Annalisa ricorda che la Payne è stata davvero una scienziata eccezionale che «tutti dovrebbero conoscere al pari di scopritori come Newton o Einstein, a cui lei deve essere associata per la sua altrettanto grandissima scoperta.»
Il secondo contributo di Annalisa Santi è dedicato ad una matematica: Alicia Boole… dai politopi ai numeri politopici. Il numero politopico è un’estensione a più di tre dimensioni del concetto di numero poligonale in due dimensioni, come il 178 che è 31-gonale. Il termine n-politopo è stato coniato da Alicia Boole, figlia di George Boole, il fondatore della logica matematica. Orfana di padre a quattro anni, venne istruita in matematica dalla madre e dallo zio, Charles Howard Hinton, che probabilmente contribuì all’ideazione degli n-politopi. Nonostante la faticosa vita familiare, non abbandonò mai le sue ricerche sui politopi, tanto da riuscire a coinvolgere il matematico olandese Pieter Hendrik Schoute: insieme realizzarono delle tavole e generalizzarono il concetto di poliedri regolari. Per il suo lavoro, ad Alicia Boole venne assegnata una laurea honoris causa nel 1914.


Anche Mauro Merlotti dello Zibaldone Scientifico ha scelto di restare in tema, riproponendo alcuni post nei quali ha parlato di Emmy Noether, la grande matematica «che ha legato il suo nome all’omonimo teorema che mette in luce la profonda connessione tra simmetrie e leggi di conservazione: in un sistema fisico, una particolare simmetria che il sistema possiede è sempre associata alla presenza di una quantità conservata. Ad esempio, se un sistema fisico è invariante rispetto a traslazioni temporali, allora il teorema di Noether implica che l’energia del sistema sia conservata. Analogamente, se un sistema fisico è invariante rispetto a traslazioni spaziali, la quantità di moto si conserva.» Il secondo post ha per protagonista la carica elettrica, il terzo parla di rottura della simmetria (e introduce l’argomento con una citazione di Hermann Weyl e una vignetta di Mordillo impagabili), mentre il quarto approfondisce ulteriormente l’argomento suggerendo anche un paio di letture.

Mauro non manca di ricordare anche il necrologio scritto da Albert Einstein sul New York Times in occasione della morte di Emmy Noether: «Negli ultimi giorni un’illustre matematica, la professoressa Emmy Noether, precedentemente legata all’Università di Gottinga e negli ultimi due anni al Bryn Mawr College, è morta all'età di cinquantatré anni... Nel campo dell’algebra, nel quale da secoli si impegnano i matematici più dotati, ha scoperto metodi che si sono rivelati di enorme importanza per lo sviluppo delle giovani generazioni di matematici... In questo sforzo verso la bellezza logica si scoprono le formule necessarie per una più profonda penetrazione nelle leggi della natura.»
Leonardo Petrillo propone, dal suo blog Scienza e Musica, un post del 2016 dedicato a Sof’ja Kovalevskaya: la vita della grande matematica viene raccontata nei dettagli, a partire dalle pagine delle dispense di Mikhail Ostrogradsky relative al calcolo differenziale e integrale che tappezzavano la sua camera di undicenne, fino al matrimonio di convenienza per proseguire i suoi studi in Germania. Qui, «grazie al supporto di Weierstrass, Sof’ja ottenne il suo dottorato in matematica summa cum laude all’Università di Gottinga.» Le citazioni tratte da I grandi matematici di Eric T. Bell aiutano a seguire le vicende di questa grande matematica, mancata troppo presto per una polmonite. Leonardo conclude riconoscendo che «Kovalevskaya merita un posto di rilievo nella storia della matematica, dato che fu la prima grande matematica russa, la terza donna nella storia a diventare docente universitario in Europa (dopo Laura Bassi e Maria Agnesi), nonché la prima a essere titolare di una cattedra di matematica.»


Ed è proprio di Maria Gaetana Agnesi che tratta il secondo post. Soprannominata Oracolo settelingue, perché a 13 anni parlava 7 lingue, dedita allo studio della matematica e della religione, tanto da trascurare i rapporti sociali, la Agnesi scrisse le Istituzioni Analitiche, ma dopo la morte del padre si dedicò completamente ad opere di carità, trasferendosi al Pio Albergo Trivulzio. Con animazioni che aiutano a visualizzare una spiegazione estremamente chiara, Leonardo ricava l'equazione cartesiana della versiera e non manca di ricordare le applicazioni in fisica, ingegneria e statistica di questa straordinaria curva, simile alla cissoide di Diocle.
In tema con il Carnevale ci sono i due video che ho realizzato per #PeopleForMath, il contest lanciato dal canale IlariaF Math. Il primo, ma ultimo in ordine di tempo, riguarda Sophie Germain, una matematica eccezionale, «un talento straordinario e un genio superiore» come scrive di lei Gauss. È vissuta tra il 1776 e il 1831 ed è la prima donna ad essere stata premiata dall’Accademia delle Scienze di Parigi. La sua vicenda si presta ad essere raccontata come un romanzo ed è quanto ci offre Cecilia Rossi con il libro Sophie Germain. Libertà, uguaglianza e matematica. Così come Sof'ja Kovalevskaja ha dovuto accettare un matrimonio di convenienza, Sophie Germain ha assunto l’identità di Antoine-August Le Blanc per accedere ai corsi dell’École Polytchnique.
Il secondo video ha per protagonista Maryam Mirzakhani, l’eccezionale matematica vissuta tra il 1977 e il 2017. La sua storia mi aveva molto colpito, quando avevo avuto occasione di vedere il docufilm realizzato da George Csicsery “Secrets of the surface” (la maggior parte delle informazioni che ho trovato sono tratte dal film). Purtroppo, non esiste ancora una biografia completa e, a parte la citazione in alcuni libri, ci sono solo libri in inglese, illustrati per bambini, come Maryam’s Magic di Megan Reid e Aaliya Jaleel e Maryam Mirzakhani di M.M. Eboch e Elena Bia. Fortunatamente parecchie notizie le ho trovate nel bellissimo The Mirzakhani Issue, con il fumetto di Davide La Rosa e Silvia Ziche “Sotto il segno del toro” e con gli articoli di Chiara De Fabritiis, Barbara Nelli, Barbara Fantechi ed Elisabetta Strickland.


Un passaggio del film mi era piaciuto particolarmente: nel 2009, dopo aver avuto una prestigiosa Clay Fellowship e una cattedra a Princeton, Maryam approda a Stanford e comincia la sua collaborazione con Alex Eskin, dell’Università di Chicago. È proprio lui a raccontare l’esperienza di lavoro con la Mirzakhani, paragonando il loro percorso a una camminata in montagna. Si tratta di una montagna inesplorata, e, a un certo punto, Alex e Maryam hanno l’impressione di poter raggiungere agevolmente la cima quando un burrone sbarra loro la strada: si tratta di una difficoltà insormontabile. Con un sorriso dolce-amaro, Eskin racconta lo scoraggiamento che hanno provato: quel burrone è costato loro due anni di duro lavoro e fatica. In tutto questo, Maryam si è mostrata positiva, anche se in un anno mezzo non ci fu nessun tipo di progresso. Per affrontare una fatica del genere, è necessario avere una grande stabilità mentale e fiducia in sé stessi.
Dopo questa bellissima carrellata di donne matematiche, procedo con i contributi “fuori tema”, ma sempre in tema matematico!
Piotr R. Silverbrahms, a nome dei Rudi Matematici, è stato il primo a propormi tre contributi e lascio la parola direttamente a lui:
Diamo i numeri…
Si tratta di un “Quick&Dirty”, ovvero un problemino della serie che raccoglie i quesiti che potrebbero sembrare semplici, ma potrebbero anche essere un po’ velenosi. Questo qui, ad esempio, ha un’esposizione composta da meno parole di quelle che stiamo usando adesso per presentarlo.
Pesci (e polli) di aprile
Il “post istituzionale”, ovvero quello che riepiloga e fornisce le soluzioni dei lettori al problema proposto sulle pagine cartacee di “Le Scienze”. Stavolta i nostri eroi giocano un vecchio gioco telepatico, uno dei due pensa un numero e l’altro deve indovinarlo. Con qualche complicazione al contorno, naturalmente…
Buon compleanno, matematici antichi!
Si tratta ovviamente di un “compleanno”, ovvero una sorta di celebrazione a un personaggio, ma in realtà è un po’ diverso dal solito. L’articolo è uscito in RM151, Agosto 2011, con il titolo “Tempio Greco” (pag.3). La situazione in cui è stato scritto è stata parecchio insolita, anzi proprio unica e irrepetibile: di solito i compleanni sono scritti da uno solo dei tre redattori, parlano quasi sempre di un solo scienziato, ed escono nel mese in cui lo scienziato in questione è nato. In questo caso, gli autori sono tre, i personaggi principali celebrati sono ben più di uno, e di nessuno di essi conosciamo la data di nascita. Abbiamo deciso di scrivere un pezzo di compleanno a testa: ognuno si è scelto un greco notevole (non chiedeteci chi ha scelto chi) e ha scritto un brano relativamente breve su di esso. Mentre scrivevamo, ci è venuto in mente che sarebbe stato carino sistemare l’articolo su tre colonne, anziché sulla solita pagina a larghezza normale. Dalle tre colonne siamo passati al tempio, e abbiamo deciso di fare un esercizio tipografico: un “compleanno” a forma di tempio greco (da cui il titolo). Se i lettori più curiosi seguono il link messo poco sopra, dovrebbero più o meno riconoscere la forma: inizia con il timpano triangolare (dove stavano le citazioni, tra cui quella di Virgilio), prosegue con un altro pezzo comune a larghezza normale (più o meno in corrispondenza del fregio e dell’architrave), poi si divide in colonne, appunto le tre colonne tipografiche ognuna delle quali parlava di un matematico. Il pezzo si chiude poi con un altro pezzo a larghezza normale, più o meno in corrispondenza architettonica con il basamento (stilobate?) dei classici templi dorici. A riportare la forma di tempio sul blog non ci abbiamo neppure provato, ci è parsa subito ragionevolmente impossibile.
«L’uomo che riesce a fare più matematica di dieci divulgatori normali» (così è stato definito da uno dei matematti), al secolo Maurizio Codogno, nonostante i molteplici impegni non delude nemmeno in questa edizione del Carnevale e propone numerosi contributi:
Ci sono i quizzini, che sono sempre un bel passatempo:
Caselle vicine, in un certo senso un problema di parità
Corda, uno di quei problemi che si possono risolvere col trucco
Tutte le cifre, una specie di gioco a incastro
Successione (non avevo molta fantasia col nome) è di tipo moltiplicativo.
Le recensioni sono uno dei più grandi contributi di Maurizio Codogno (e potete seguire le sue tracce anche negli store online)
Recensioni della collana Matematica:
L’infinito, di Maurizio Codogno: da Zenone a Cantor e oltre.
I numeri reali, di Salvatore Fragapane. Uno sguardo più diretto su una pura creazione umana.
Le basi dell’analisi, di Davide Calza e Riccardo Moschetti: dalle successioni ai limiti.
Matematica e Musica, di Moreno Andreatta; molto di più di quanto si pensi di solito per le connessioni.
Altre recensioni:
La teoria dell’informazione, di Giuseppe O. Longo, nella collana kiosk “Lezioni di fisica”: più filosofia dell’informazione che teoria vera e propria.
Dal bit al qubit, di Carlo Biancardi. La parte quantistica è interessante, l’altra ben difficile da leggere.
Nel mercoledì matematico:
Triangoli equivoci, dove viene mostrata una variante dell’illusione del quadratino mancante
Negli anni ‘90 i computer usavano un’implementazione della radice quadrata inversa che leggeva numeri reali come se fossero interi.
Quando scommettere sull’arrivo dell'idraulico? Un paradosso forse più psicologico che matematico.
Stavolta mostro come si possano risolvere certi problemi sulle frazioni senza fare conti
Il contributo di Flavio Ubaldini, autore del blog Pitagora e dintorni, in arte Dioniso, è la seconda parte di Maieutica e duplicazione del quadrato (qui la prima parte). Si tratta di una breve narrazione ispirata al Menone di Platone e l’estratto che ci viene fornito aiuta a farsi un’idea del contenuto:
... «Ma quanto misura allora questo maledetto lato!», starnazzò Eudosso spazientito.
«Non lo so, per Zeus! Non lo so!», fece Menone sconfortato. «Fa freddo! Lasciatemi tornare al lavoro».
«Calma, non scoraggiarti», disse Teeteto mentre Platone rimproverava nuovamente Eudosso.
In altre parole, il processo di apprendimento non è lineare e, al tempo stesso, è ricco di frustrazione e spesso vittima dello scoraggiamento. Aspettiamo la terza puntata per gustarci il senso di vittoria di Menone alla fine del percorso.
Anche Gianluigi Filippelli, dal blog DropSea, propone le sue recensioni dei volumi della serie Matematica in allegato con la Gazzetta dello Sport:
La statistica di Alessandro Viani
L’infinito di Maurizio Codogno
I numeri reali di Salvatore Fragapane
Le basi dell’analisi di Davide Calza e Riccardo Moschetti
Matematica e musica di Moreno Andreatta
Gianluigi propone anche un post della serie dei Rompicapi di Alice, Una questione di segni, dedicato ai segni di somma, sottrazione e moltiplicazione, con particolare attenzione alla regola del – * – = +
Dal Caffè del Cappellaio Matto, invece, ecco Topolino #3524: Detective matematico, con all’interno il video di Disney Comics&Science dedicato a una vignetta particolare di una storia uscita su Topolino che ha permesso a Gianluigi di raccontare una piccola storia su Bertrand Russell e la fondazione della matematica.
Il Carnevale si chiude alla grande con i numerosi contributi di MaddMaths! e lascio la parola direttamente a Marco Menale:
Dal 2019, il 12 maggio si celebra la Giornata Internazionale delle Donne nella Matematica. Questa data non è stata scelta a caso, anzi. Il 31 luglio 2018, durante l’evento del World Meeting for Women in Mathematics, si è deciso di ricordare la nascita della prima donna a essere stata insignita della Medaglia Fields, ovvero la matematica iraniana Maryam Mirzakhani, che ha ricevuto il prestigioso riconoscimento nel 2014 ed è purtroppo mancata pochi anni dopo.
La giornata del 12 maggio vuole quindi essere un’occasione per “ispirare le donne di tutto il mondo a celebrare i loro risultati in matematica e incoraggiare un ambiente di lavoro aperto, accogliente e inclusivo per tutti” (trad. da qui). Tale scopo è promosso e incoraggiato anche attraverso iniziative di vario genere rivolte a pubblici eterogenei.
Quali sono gli eventi in programma in Italia? Li sta raccogliendo Alice Raffaele in Giornata Internazionale delle Donne nella Matematica 2024 – Tutti gli eventi italiani [AGGIORNATO]. Vi invitiamo a segnalarcene altri mancanti attraverso i commenti o scrivendo a Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo..
Nell’articolo I gioielli della Matematica presentiamo un progetto realizzato da Alessandro Zaccagnini con le docenti Maria Chiara Gullo e Lorenza Serventi in due classi dell’Istituto Comprensivo “Guatelli” di Collecchio (Parma) nel quale abbiamo preso alcuni elementi di un laboratorio svolto nell’ambito del Piano Nazionale Lauree Scientifiche nel Liceo Classico “G.B. Romagnosi” di Parma. L’obiettivo finale è dare una dimostrazione “combinatoria” del Piccolo Teorema di Fermat mediante la costruzione di piccoli gioielli.
Continua la serie La Matematica è piena di Eulero! a cura della redazione di MaddMaths!. Dopo i primi due episodi, infinità dei numeri primi e le equazioni della fluidodinamica, sono fuori:
Episodio 3: La più bella formula della matematica di Chiara de Fabritiis;
Episodio 4: Il problema di Basilea di Sandra Lucente.
Giovedì 26 marzo 2024 è venuto a mancare a Firenze, dove risiedeva, Enrico Giusti, matematico, storico della scienza, comunicatore. Su MaddMaths l’abbiamo ricordato in due articoli: Enrico Giusti, storico della matematica a cura di Paolo Freguglia e Enrico Giusti e la comunicazione della matematica a cura di Sabina Tessieri, direttrice del Museo “Il Giardino di Archimede” dal 2004 al 2023.
Save the date: Women and Space ai Lincei – 28 maggio 2024 Si terrà presso l’Auditorio dell’Accademia Nazionale dei Lincei il prossimo 28 maggio il Convegno “Women and Space”, durante il quale si avvicenderanno in una serie di conferenze sei scienziate che hanno contribuito al progresso delle scienze spaziali in diversi settori: osservativo, matematico, tecnico, astronautico e divulgativo. Le oratrici di eccezione sono:
Marica Branchesi (GSSI)
Simonetta Cheli (ESA-ESRIN)
Francoise Combes (College de France/Obs. Paris)
Susanna Terracini (Università di Torino)
Giovanna Tinetti (University College London)
Ersilia Vaudo Scarpetta (ESA)
Rivoluzioni matematiche: la congettura di Poincaré di Nicola Ciccoli Con il numero di Maggio de Le Scienze troverete in allegato il ventesimo dei trenta volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato alla congettura di Poincaré e alla sua dimostrazione ottenuta nel 2003 da Grigorij Perel’man, ed è scritto da Nicola Ciccoli.
Per le News di Stefano Pisani:
Scoperto per la prima volta un frattale a livello molecolare I frattali sono ovunque in natura: si possono scorgere strutture frattali nei delta dei fiumi e tra i rami degli alberi. Si tratta di forme che hanno lo stesso sviluppo sia da lontano sia quando vengono viste, ingrandite, più da vicino. Alcuni frattali, detti frattali regolari, sono identici su scale diverse come, per esempio, i vortici dei broccoli romani, ma frattali regolari non sono mai stati individuati a livello molecolare. Fino ad oggi.
Nuovo modello matematico spiega come si muovono i batteri (e il traffico) La marcia di automobili su un’autostrada e il movimento dei batteri verso una fonte di cibo hanno una cosa in comune: in ogni momento possono dare origine a fastidiosi ingorghi che, soprattutto nel caso delle vetture, saremmo lieti si scoprire come sciogliere. La ricerca è stata pubblicata sul Journal of Statistical Mechanics: Theory and Experiment.
Per La Lente Matematica di Marco Menale:
Armi nucleari, deterrenza e dilemmi Il dibattito sulle armi nucleari torna periodicamente in primo piano. Si parla di deterrenza, ma fino a che punto? A questo dilemma dedicò alcune riflessioni il matematico Anatol Rapoport.
Disuguaglianze e informazione: l’indice di Theil La misura delle diseguaglianze fornisce informazioni per la comprensione di un fenomeno; succede in economica con la distribuzione della ricchezza. Ci sono vari indici per quantificare la disuguaglianza a partire da un insieme di dati. È il caso dell'indice di Theil.
Per Letture Matematiche:
Chi dice e chi tace, Chiara Valerio Tra ricostruzioni e coperture, una recensione di “Chi dice e chi tace”, l’ultimo libro di Chiara Valerio, che rivela alcune strutture matematiche tra le righe attraverso riferimenti a geometria integrale, ricerca operativa, enumerazione e teoria della complessità, con un pizzico di etimologia. A cura di Alice Raffaele.
In questo libro i conti non tornano È stato pubblicato di recente per le edizioni Einaudi il libro “La seconda prova”. Imparare la matematica vent’anni dopo, scritto da Pietro Minto, che parla del rapporto dell’autore, da adulto, con la matematica. Lo ha letto e commentato per noi Daniele Gouthier.
Matematica al plurale – oltre il pregiudizio, voci dalla didattica – il trailer del nuovo podcast
Matematica. Se pensiamo a quanti modi ci sono di concepirla, impararla, percepirla nel mondo e nel tempo, che variano da soggetto a soggetto, verrebbe forse da pensarla al plurale: “Matematiche”. Anche perché riguarda tutte le persone: fin dal suo apprendimento, la matematica ha un impatto rilevante sulle nostre vite e spesso si lega a emozioni forti, tra cui la paura di fallire. I voti in matematica continuano a terrorizzare generazioni di studenti e studentesse. Perché succede? Come riconciliarsi con questa disciplina bellissima, ma spesso odiata? Fino a che punto il suo insegnamento può far fronte alle sfide dettate dall’evoluzione tecnologica?
Ne parliamo in Matematica al plurale – Oltre il pregiudizio, voci dalla didattica, un podcast a cura della CIIM (Commissione Italiana per l'Insegnamento della Matematica), in collaborazione con l’AIRDM (Associazione Italiana di Ricerca in Didattica della Matematica), pubblicato da MaddMaths! e disponibile dal 18 maggio sulle maggiori piattaforme di streaming audio.
L’8 maggio si è svolto nell’aula Carlo Ciliberto dell’Università degli Studi di Napoli Federico II, vista anche la ricorrenza degli 800 anni dalla sua fondazione ad opera del sovrano svevo, l’evento UMI per la Festa delle Donne Matematiche (May12). L’evento, oltre che dall’UMI, è stato organizzato dal Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, con la collaborazione di MaddMaths!, del CECAM e il patrocinio dell’INdAM. Ci racconta com’è andata Chiara de Fabritiis, coordinatrice del Comitato Pari Opportunità dell’UMI, nell’articolo L’evento May12 UMI a Napoli – reportage anche fotografico.
Questo è quanto…
Direi che la rassegna offre, come sempre, matematica per tutti i gusti!
Inesauribile caparbietà
Ho pochi ricordi del mio rapporto con la matematica alla scuola primaria, forse perché mi veniva facile e naturale, ma mi è rimasto impresso il disegno alla lavagna di un trapezio e la sua trasformazione in un triangolo equivalente, a spiegare perché per calcolare l’area fosse necessario sommare le basi e moltiplicarle per metà altezza. Forse in quel momento mi sono innamorata della geometria.
I ricordi più vividi sono quelli della scuola media: ricordo quando il professore assegnava delle espressioni da svolgere e le proponeva come sfida alla classe, tanto che in quei momenti, quando capitava che due persone si alzassero nello stesso momento, si assisteva a vere e proprie gare di corsa per raggiungere prima la cattedra. Ricordo, in particolare, che a volte arrivavi alla cattedra, soddisfatto del tuo lavoro e trepidante, ma il professore scuoteva la testa guardando il risultato e allora tornavi al tuo banco per riprovare, intestardendoti alla ricerca della strada corretta.
Del percorso liceale ricordo che l’errore in matematica ha cominciato a presentarsi con una maggiore frequenza, se penso ai problemi di geometria euclidea e analitica o di trigonometria, magari con tanto di discussione e sistemi parametrici al seguito. Capitava di intestardirsi su un problema che non dava il risultato corretto: al mattino, condividevo la mia frustrazione con mia cugina, che era in una classe parallela alla mia, e mi confrontavo con lei, che magari stava litigando con lo stesso problema (avevamo lo stesso insegnante) e ne parlavamo, ripercorrendo insieme le fasi della soluzione, mentre camminavamo verso la scuola. A volte succedeva che trovassimo la soluzione prima di arrivare in aula, e trascrivere i passaggi sul quaderno era solo la conferma di quanto avevamo già capito lungo il cammino. Altre volte, ancora, mi capitava di continuare a pensare al problema durante tutto il pomeriggio, senza riuscire a trovare una soluzione, ma al mattino mi svegliavo con la consapevolezza di conoscere quella soluzione e, prendendo in mano carta e penna, verificavo i passaggi, prima ancora di essere completamente sveglia: è stato in quel momento che ho capito l’importanza del “dormirci su”. Ancora adesso, con maggiore consapevolezza, se ho un problema che non riesco a risolvere (che sia di matematica o di altro) ci penso un attimo prima di addormentarmi, perché la mia testa possa continuare a lavorarci mentre riposo. È la stessa strategia che suggerisco ai miei alunni (per quanto, durante una verifica sia un po’ più difficile riuscire a “dormirci su”…). Mi fa ripensare a Poincaré che, dopo essersi concentrato a lungo e inutilmente su un problema, decise di partire per un gita e, mettendo piede sull’omnibus di Coutances, riuscì a trovare la soluzione (secondo il racconto fatto nel libro Le ostinazioni di un matematico, che racconta l’originale storia di Armand Duplessis, che avrebbe sprecato la propria vita nel tentativo di dimostrare la congettura di Goldbach).
Credo si sia colto il comune denominatore di questi tentativi: la testardaggine… e se penso al percorso universitario, questa mia caratteristica ha avuto un ennesimo banco di prova. Mi sono ritrovata nelle parole di Roberta Fulci che, durante la diretta con Ilaria Fanelli, Una matematica a Radio3 Scienza, ha risposto alla domanda di uno spettatore che chiedeva di essere rassicurato in merito alle sue difficoltà universitarie: Roberta ha raccontato che, avendo scelto matematica dopo il liceo classico, si è trovata ad affrontare grandi difficoltà durante il primo anno di corso ed ha avuto la sensazione di passare “dall’essere brava all’essere un rapa”. Come al solito, Roberta ha espresso il concetto in modo colorito e simpatico, come è tipico suo, e io ho capito perfettamente cosa intendesse, perché l’ho provato sulla mia pelle, anche se avrei dovuto essere più facilitata di lei, visto che alle spalle avevo un liceo scientifico! In realtà, arrivare alla fine del mio percorso universitario, alla tanto desiderata laurea in matematica, ha richiesto un bel po’ di caparbietà, tanto che a chi mi chiedeva che cosa avessi imparato dal mio percorso universitario rispondevo: “Ho imparato ad abbattere i muri a testate”.
Ho concluso il percorso universitario, nonostante… nonostante tutto! Per questo, forse, ho sempre ritenuto la caparbietà una componente fondamentale della buona riuscita in matematica. Addentrandomi sempre più nella storia della matematica, ho scoperto che essa è costruita sulla determinazione, sulla tenacia, sulla caparbietà. Uno dei primi libri che ho letto è L’ultimo Teorema di Fermat di Simon Singh: i tentativi di dimostrare il teorema si dipanano lungo i secoli, dando luogo a una staffetta espressione di un lavoro corale, come se ognuno dei matematici che ha preso parte a questo percorso avesse contribuito alla soluzione del puzzle apportando la propria piccola tessera, fino ad arrivare al risultato finale di Andrew Wiles. Per questo, forse, si parla di comunità matematica, pensando a quelle occasioni in cui i singoli matematici concentrano tutti le proprie forze per raggiungere un obiettivo comune, attraverso un lavoro continuo.
La mia convinzione che determinazione e caparbietà possano essere un’arma vincente anche a scuola mi ha portato a proporre, all’inizio di ogni percorso scolastico, una citazione di John Wooden, uno dei più grandi allenatori nella storia del basket delle università americane:
«Quando si migliora un po’ ogni giorno, alla fine si raggiungono grandi risultati. Quando si aumenta l’allenamento giorno dopo giorno, si ottiene un netto miglioramento della forma fisica. Non sarà domani, né dopodomani, ma poi i progressi saranno notevoli. È inutile puntare a grandi risultati in tempi brevi, conviene invece cercare di migliorare un po’, un giorno dopo l’altro. È l’unico modo per ottenere risultati duraturi.»
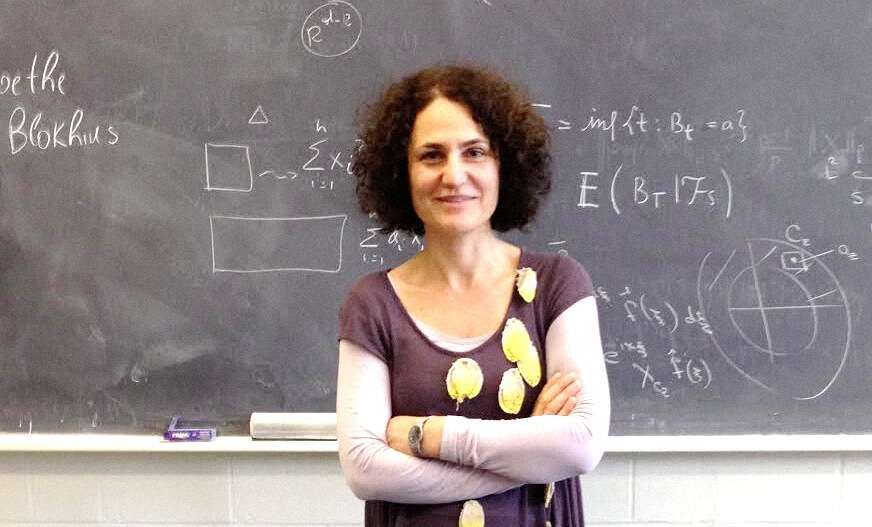
Gigliola Staffilani, prima donna italiana full professor al MIT, alla domanda rivoltale da Roberto Natalini in un’intervista del 2018 «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?» ha dato una bella risposta: «Credo che l’intuizione arrivi quando ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte.» Secondo la leggenda, pare che al re Tolomeo, che chiedeva un metodo rapido per studiare la geometria, Euclide abbia risposto che non esistono “vie regie”, ovvero percorsi privilegiati: in altre parole, ci sono stati matematici grandissimi nella storia, ma questo non significa che per loro le cose siano state più facili, perché avevano talento. Il duro lavoro resta una componente fondamentale per la buona riuscita in matematica!
Nei giorni scorsi, durante una lezione nella mia terza liceo scientifico, mentre le idee continuavano ad accumularsi intorno al tema della caparbietà, ho chiesto ai miei alunni quale potesse essere la caratteristica che una persona deve possedere per garantirsi un successo in matematica. Sono rimasta molto colpita dalle loro risposte: innanzi tutto perché molti di loro, invece di indicarmi una caratteristica, hanno risposto fornendo una strategia, che passava attraverso il ragionamento, la comprensione o la spesa di un po’ di tempo per creare collegamenti mentali, ma qualcuno ha risposto: «bisogna sapere le regole per poterle applicare meccanicamente» e, davanti alle mie proteste, si è difeso parlando di una strategia personale. Mi ha colpito, inoltre, che qualcuno ritenga importante il calcolo o “farsi piacere la matematica”, perché se è vero che, per certi aspetti, l’apprendimento è reso più facile dalla passione, non è certo possibile imporsi a comando di amare una disciplina. Dopo aver indicato la necessità di fare molti esercizi, qualcuno ha parlato di perseveranza e costanza, della capacità di non abbattersi per un risultato negativo, di forza di volontà e determinazione… e poi c’è il mio foglietto con scritto: caparbietà.

Ho voluto approfittare di queste risposte per riflettere con loro, a partire dalla storia di Sophie Germain (è mia intenzione partecipare a #peopleformath2024 lanciato dal canale IlariaF Math…). La sua vicenda biografica ha tutte le caratteristiche di un romanzo, con l’assunzione dell’identità di Antoine Le Blanc, per poter interloquire con i matematici più importanti dell’epoca come Lagrange e Gauss, e per approfondire la sua vita ho fatto riferimento al libro di Cecilia rossi Sophie Germain. Libertà, uguaglianza e matematica.

Al momento di costruire una bibliografia, mi sono imbattuta anche in Nothing stopped Sophie, di Cheryl Bardoe, con le illustrazioni di Barbara McClintock: si tratta di un libro per bambini, disponibile solo nella versione inglese, nel quale troviamo, ripetuto più volte, “Nothing stopped Sophie”, perché effettivamente niente riuscì a fermarla! Nel momento in cui i suoi genitori hanno cercato di ostacolarla nella sua passione per la matematica, lei ha trovato il modo di andare avanti, ad esempio.

Le donne che hanno scritto di lei considerano la caparbietà uno dei suoi lati più positivi, ma non è così se la sua vicenda viene interpretata da uomini: nel libro Il genio delle donne, Piergiorgio Odifreddi ha dedicato alla Germain il capitolo La prima vera matematica, ma non le risparmia il suo sarcasmo, visto che la definisce una giovane dal «carattere difficile e [dai] modi arroganti». Parlando poi del suo scontro con l’astronomo Joseph de Lalande, che l’aveva omaggiata del suo “Astronomia per le dame”, una delle pubblicazioni dell’epoca che trattava le donne con condiscendenza e proponendo una divulgazione in versione semplificata, dice che lei «disdegnava i testi divulgativi, e rivolse presto la sua attenzione alle difficili Disquisizioni aritmetiche», come se in realtà Sophie Germain peccasse di presunzione e non fosse realmente in grado di comprendere un testo del genere. Come insegnante ho imparato a considerare la presunzione e l’arroganza una necessità, per i giovani: senza presunzione, non potrebbero mettere in dubbio i tanti “ipse dixit” con i quali si trovano a confrontarsi quotidianamente, e senza un po’ di arroganza non avrebbero il coraggio di competere con gli adulti. Franco Pastrone, del Dipartimento di matematica dell’Università di Torino, nel suo intervento per l’Associazione Subalpina Mathesis, che è diventato l’introduzione nel libro di Maria Rosa Menzio Il Signor Le Blanc, ha un giudizio a tratti tranchant: riferendosi all’infanzia, parla di episodi «forse un po’ forzati al fine di esaltare la determinazione della ragazza», che descrive come una persona timida in pubblico, anche se, quando si trattava di ottenere dei risultati scientifici «la sua timidezza scompariva, anzi riusciva a mostrare una cocciuta aggressività».
Mi è parso quasi di cogliere che questa caparbietà, così positiva quando esercitata dagli uomini, diventasse un aspetto quasi negativo se declinato al femminile. Eppure, quando parliamo di Andrew Wiles, la sua determinazione viene celebrata, e la sua capacità di isolarsi dal resto del mondo per lavorare in autonomia alla dimostrazione non viene presa per presunzione, semmai gli viene riconosciuto il coraggio di aver rischiato tanto. Andrew Wiles ha avuto il coraggio di affrontare una sfida che aveva attraversato i secoli e, quando viene individuato un errore nella sua dimostrazione, prova a correggersi, impegnando altro tempo.

Non parla di presunzione, Gauss che, una volta conosciuta l’identità di Sophie Germain, le scrive:
«Il fascino di questa scienza sublime si rivela in tutta la sua bellezza solo a chi ha il coraggio di esplorarla. Una donna, a causa del suo sesso e dei nostri pregiudizi, incontra molti più ostacoli di un uomo nel familiarizzarsi con problemi complessi. Tuttavia, quando supera queste barriere e penetra nelle profondità più recondite, rivela di possedere il coraggio più nobile, un talento straordinario e un genio superiore.»
Per concludere, non può mancare un riferimento all’ultimo premio Abel, Michel Talagrand, che dichiara che «il segreto del successo in matematica è di lavorare ogni giorno fino a essere esausti ma non di più». Ne parlano, con dovizia di particolari, Beatrice Mautino ed Emanuele Menietti nel podcast del Post Ci vuole una scienza: Talagrand parla delle proprie difficoltà in matematica, legate a un “cervello lento” e a una “memoria terribile”, eppure dichiara di aver usato questo metodo proprio per superare le sue difficoltà. E direi che, visti i successi, non ci resta che fidarci!
Ricordo ora che anche Maryam Mirzakhani si è sempre definita una matematica lenta, ma è riuscita, nella sua breve vita, a raggiungere risultati eccezionali. Alex Eskin, dell’Università di Chicago, con il quale ha collaborato a lungo, racconta, nel film Secrets of the Surface, l’esperienza di lavoro con Maryam, paragonando il loro percorso a una camminata in montagna. Si trattava, come spesso succede, di una montagna inesplorata, e, a un certo punto, i due matematici hanno avuto l’impressione di poter raggiungere agevolmente la cima, quando un burrone ha sbarrato loro la strada. Con un sorriso dolce-amaro, Eskin racconta lo scoraggiamento che hanno provato, dato che quel burrone è costato loro due anni di duro lavoro e fatica. In tutto questo, Maryam si è mostrata positiva, anche se per un anno mezzo non ci fu nessun tipo di progresso. Per affrontare una fatica del genere e uscirne vittoriosi, è necessario avere una grande stabilità mentale e fiducia in sé stessi.
Aggiungendo queste caratteristiche alla caparbietà, credo proprio che il successo sia assicurato!
Cerchi tra i banchi
Si può dire che p sia il protagonista del programma di seconda liceo scientifico: nella prima parte dell’anno scolastico, ci si immerge nell’insieme dei numeri reali e gli irrazionali sono posti al centro della scena. Come dimenticare l’irrazionale per eccellenza?

Nell’immagine è riportata una rappresentazione visiva di alcune cifre decimali di p, 180 per la precisione, che è facile ricostruire assegnando al colore la cifra corrispondente. L’immagine è stata realizzata per uno dei cartelloni esposti durante la seconda partecipazione al Festival di BergamoScienza dell’istituto dove insegno, che ha avuto come protagonista il cerchio.
La classe seconda è il momento in cui si alza il livello di difficoltà: dopo aver risolto equazioni, disequazioni e sistemi lineari, si affrontano, con gli irrazionali nella cassetta degli attrezzi, i problemi di secondo grado ed ecco che in geometria fa la sua comparsa la circonferenza, definita come il luogo geometrico dei punti del piano equidistanti da un punto fisso, il centro.
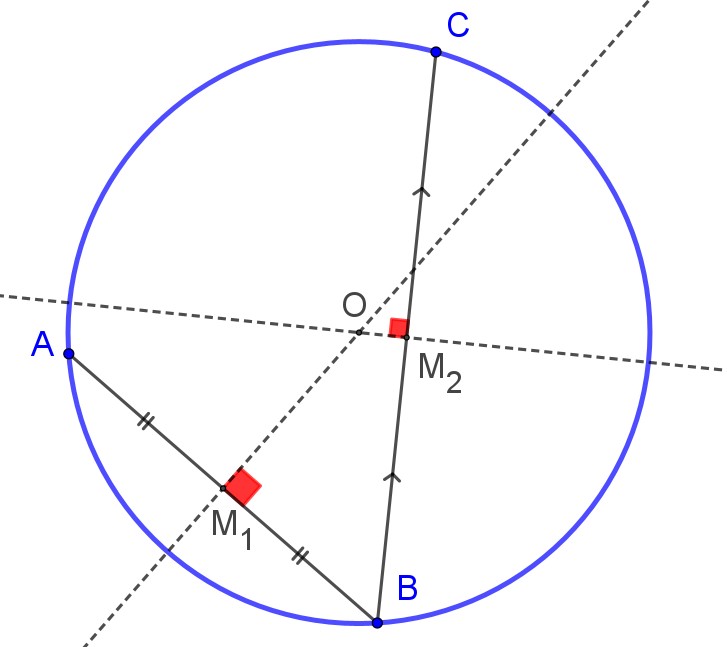
Uno dei primi teoremi che si incontrano riguarda la circonferenza passante per tre punti non allineati, e la dimostrazione permette, in realtà, di fare una semplice costruzione con Geogebra, evitando di usare lo strumento “Circonferenza – tre punti”. Il teorema fa intravedere i teoremi sulle corde, che presto permetteranno di vederne la lunghezza in relazione alla loro distanza dal centro, e di realizzare che davvero l’asse di una corda passa per il centro.
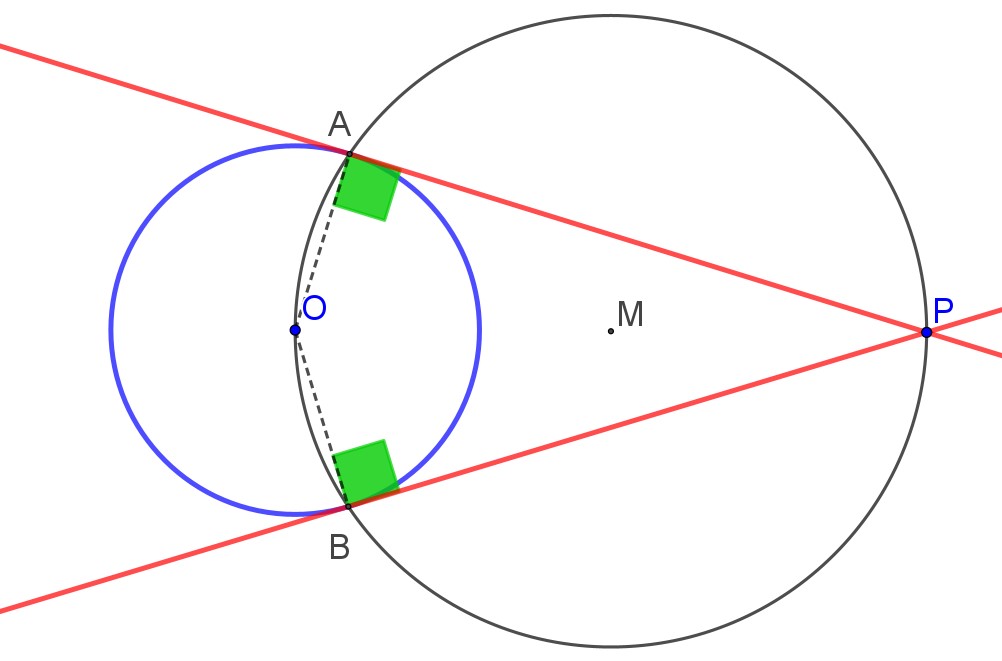
Il passo successivo è quello di considerare le circonferenze in relazione alle rette e, in particolare, in relazione alle tangenti. Così, può capitare di dover imparare a costruire le rette tangenti a una circonferenza tracciate da un punto esterno, basandosi sul fato che una retta tangente a una circonferenza è perpendicolare al raggio passante per il punto di tangenza. Questo risultato ci regala un anticipo sui triangoli rettangoli inscritti in una semicirconferenza.
Il percorso in matematica assomiglia a una danza, con un passo avanti e uno indietro, a creare una coreografia, ritornando su cose già viste, ma affrontandole in maniera diversa, e così nel capitolo successivo le circonferenze incontrano i triangoli, sempre inscrivibili in e circoscrivibili a una circonferenza, ma non solo:
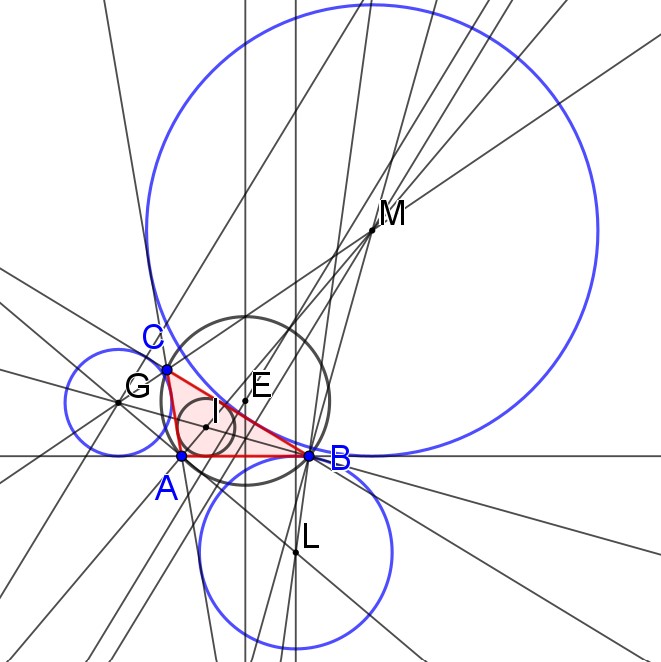
Tra il circocentro (E) come punto di incontro degli assi e centro della circonferenza circoscritta, l’incentro (I) punto di incontro delle bisettrici e centro della circonferenza inscritta, il triangolo ABC incontra anche altre tre circonferenze, di centri rispettivamente M, L e G, detti excentri, punti di incontro della bisettrice dell’angolo interno non adiacente con le bisettrici degli altri due angoli esterni e quelle blu sono le circonferenze exinscritte, tangenti a un lato e al prolungamento degli altri due. È stato vedendo un’opera di Lanfranco Bombelli (1921/2008), pittore, incisore e architetto, che ho pensato a questa rappresentazione e…
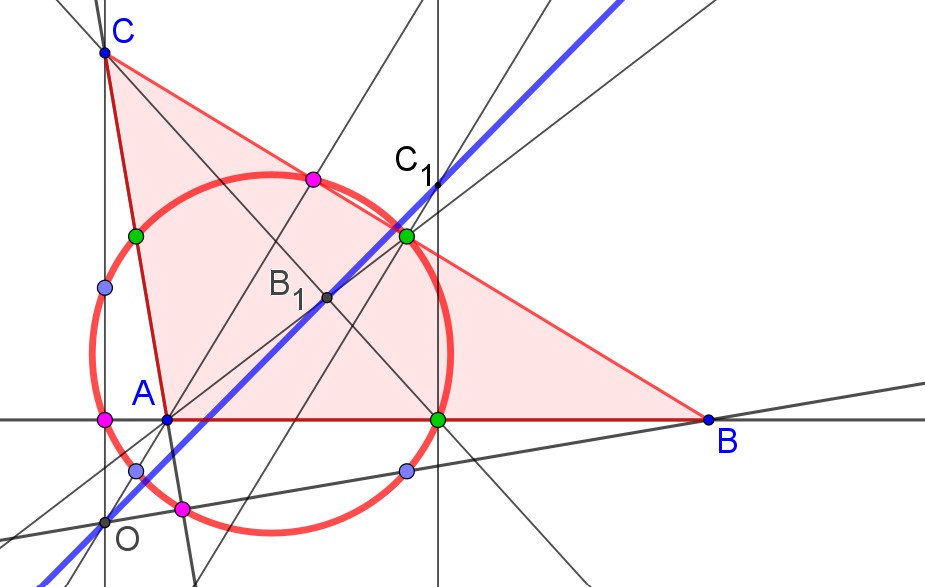
Ripensare al Cerchio per nove punti è stato un attimo: eccola in tutta la sua bellezza! Indicata in rosso passa per tre terne di punti: quelli rappresentati in verde sono i punti medi dei lati del triangolo; quelli in fuxia sono i piedi delle altezze relative ai lati e poi ci sono gli ultimi, più difficili da definire, perché, individuato con O l’ortocentro (il punto di incontro delle altezze di un triangolo), essi sono i punti medi del segmento che ha per estremi O e un vertice del triangolo. Ho scoperto, giusto oggi, che questa circonferenza è nominata come Cerchio di Feuerbach (almeno, stando a quanto dichiarato su Wikipedia), matematico tedesco, fratello del più famoso filosofo. Qualcuno, invece, la nomina come cerchio di Eulero, ma credo che, in questo caso, il celebre matematico potrebbe accontentarsi della paternità della retta, che passa per tre punti notevoli: ortocentro, baricentro, circocentro.
Mentre scorro le pagine del libretto di Bruno Munari intitolato Il cerchio (e scopro ora che ci sono anche Il quadrato e Il triangolo…) dove ho trovato il riferimento a Lanfranco Bombelli, mi imbatto nelle voci “Raggio decrescente” e “Raggio crescente”:
Mi è parso così interessante, che non ho resistito alla tentazione di realizzare quello crescente con Geogebra, arrivando fino al poligono di 14 lati (inventandomi metodi ingegnosi per rappresentare quelli da 7, 9, 11 e 13 lati). Mi piace citare, in particolare, ciò che scrive Munari, oltre alle indicazioni per la costruzione: «Può sembrare che il raggio, aumentando oltre ogni limite, diventi infinito; invece si avvicina a un limite che è circa dodici volte quello del raggio del cerchio primitivo», esattamente come quello decrescente «si avvicina a un limite che è circa un dodicesimo di quello del raggio del cerchio primitivo».
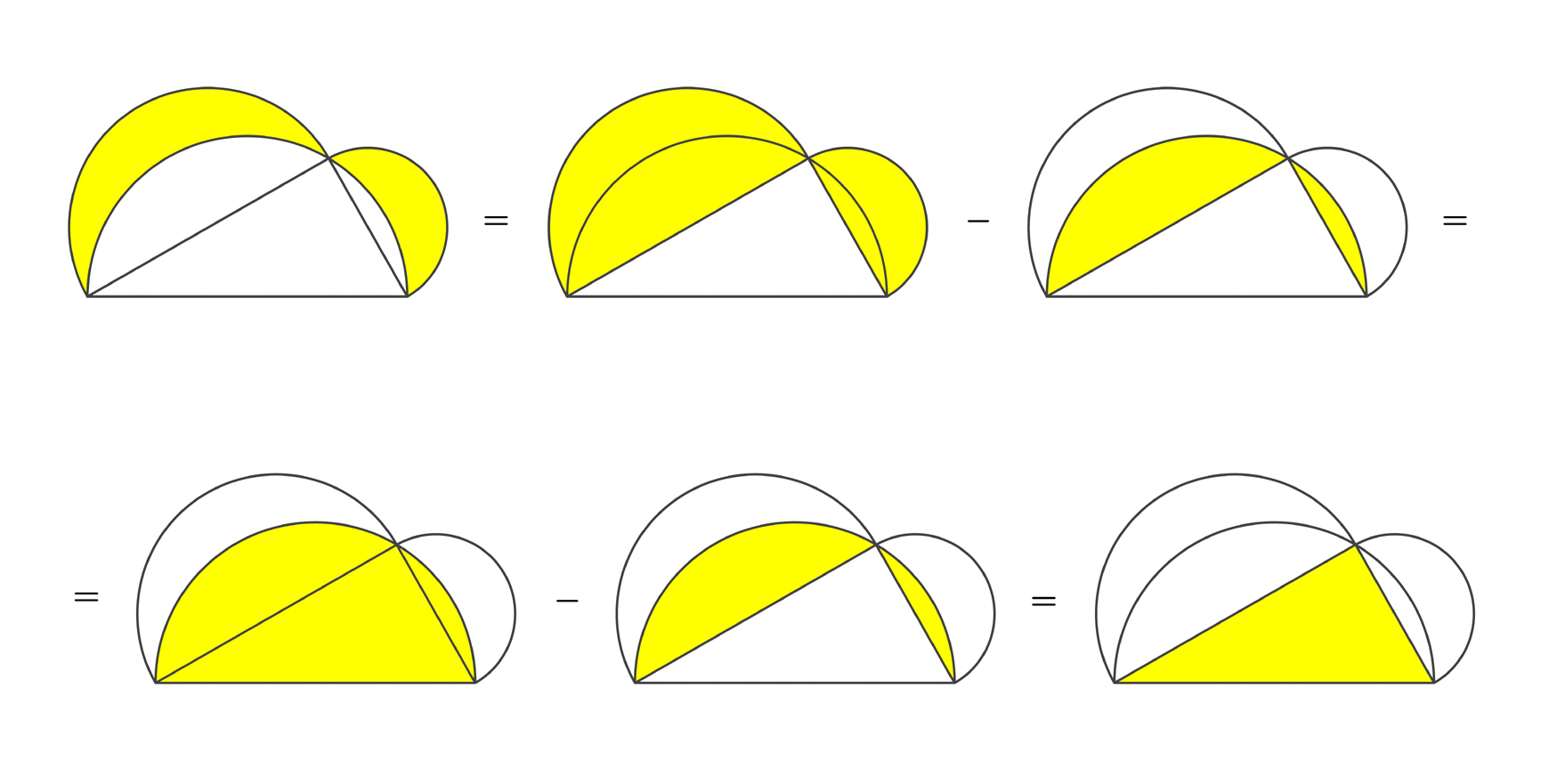
Non ho resistito alla tentazione di riprendere in mano anche questa simpatica dimostrazione senza parole, che utilizza le lunule e il triangolo di Pitagora. Il triangolo rappresentato è rettangolo e ha come lato di appoggio l’ipotenusa. Sui due cateti vengono costruite (e colorate) le lunule, la «parte di piano compresa fra due archi circolari di raggio diverso aventi in comune gli estremi e giacenti dalla stessa parte rispetto alla corda comune». In questo caso, il raggio delle semicirconferenze esterne è pari a metà del cateto e il centro è il punto medio del cateto, mentre l’arco più interno è la semicirconferenza con raggio pari a metà dell’ipotenusa e centro nel punto medio della stessa. La prima differenza è facile, la seconda, invece, ha a che fare con il teorema di Pitagora: come riportato sul sito del Giardino di Archimede, il museo della matematica: «Nell’enunciato del teorema di Pitagora, i quadrati possono essere sostituiti da altre figure, come ad esempio triangoli, esagoni, o anche figure irregolari, purché simili tra loro». Chi ha avuto modo di visitare il museo, avrà provato a mettersi alla prova con i diversi puzzle realizzati proprio con questo teorema di Pitagora generalizzato.
Sul sito, troviamo poi il caso particolare delle lunule di Ippocrate:
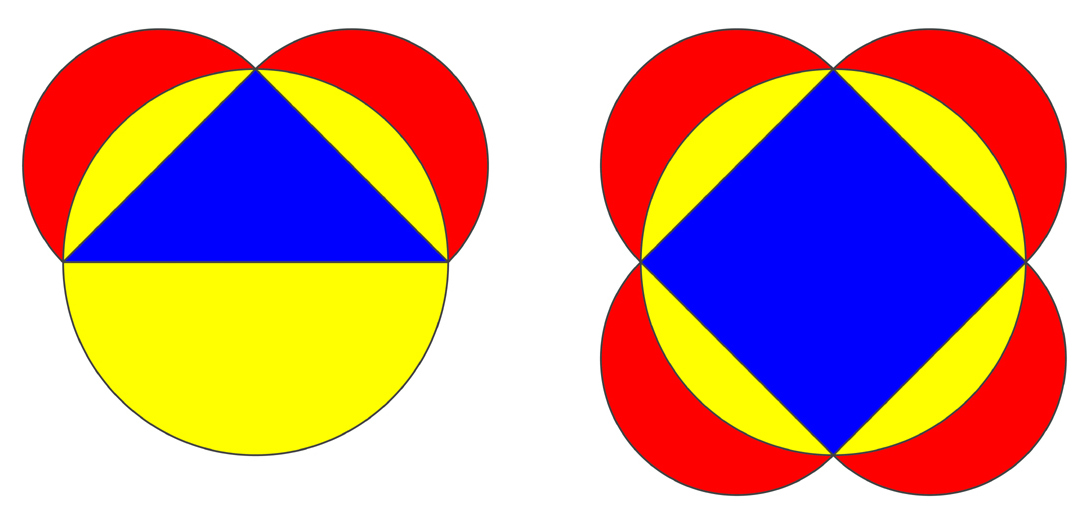
In questo caso, l’area indicata in rosso ha la stessa estensione di quella indicata in blu.
«Se poi il triangolo è isoscele, una lunula è uguale a mezzo triangolo. Questo è il primo caso storicamente accertato (la dimostrazione è attribuita a Ippocrate di Chio) in cui si è dimostrato che una figura rettilinea (il triangolo) è uguale a una curvilinea (la lunula).» Questo ci porta al logo della Mathesis:
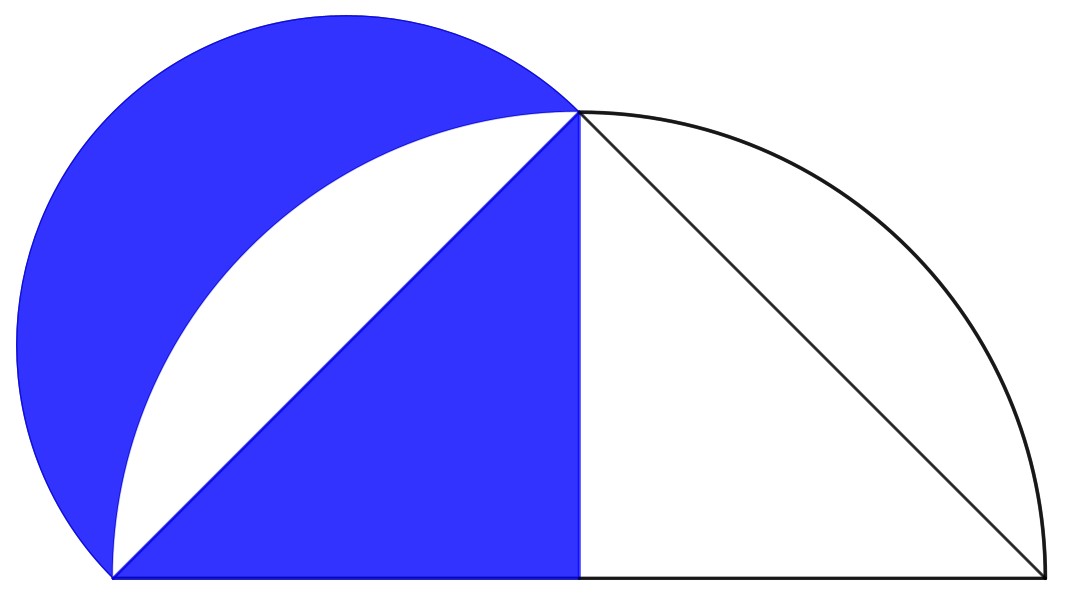
Una scelta non casuale, visto che la Mathesis è la «Società italiana di scienze matematiche e fisiche fondata nel 1895».
Il 14 marzo è, dal 2020, la Giornata internazionale della matematica e quest’anno il tema dei festeggiamenti è: Giocare con la matematica. Non potevano mancare un paio di giochi, in chiusura, presi dalle ultime due edizioni di Matematica senza Frontiere:

L’immagine a sinistra è stata proposta quest’anno: dopo averne indicato la costruzione, si chiedeva di determinare l’area della parte colorata, in funzione del lato del quadrato (indicato con a). continuando la tassellazione con altre circonferenze, è stato abbastanza semplice sottrarre, dall’area della circonferenza con raggio pari a metà diagonale del quadrato, un quadrato di lato a e moltiplicare il risultato per 2, ottenendo . Il disegno più colorato, invece, è stato proposto nella competizione dell’anno scorso e dovrebbe rappresentare la finestra con il vetro temperato di una chiesa. Sapendo che per il verde sono stati usati 400 cm2 di vetro, che superficie è necessaria per ricoprire il blu? (E scopriamo che si tratta ancora di 400 cm2).
Il cerchio è davvero una figura eccezionale e Munari dichiara nell’introduzione del suo libretto: «Il cerchio è una figura essenzialmente instabile, dinamica: dal cerchio nascono tutti i ruotismi, tutte le inutili ricerche del moto perpetuo». E dal cerchio è giunto a noi p, come dimenticarlo?
Buon pi-day a tutti!
PS: In allegato i file Geogebra per realizzare le immagini
Saltando da un pensiero all'altro
2 gennaio 2024: dopo essere stato fermo un turno a dicembre, il gruppo del Carnevale della Matematica viene richiamato all’ordine. Flavio Ubaldini invita i partecipanti a produrre i propri contributi, offrendo come tema la matematica bisestile.
Mumble mumble…
A me viene in mente solo “anno bisesto, anno funesto”, ma sulla stessa linea trovo “anno bisesto che passi presto”, “anno bisestile chi piange e chi stride”, ma credo che, pur parlando di matematica, Flavio non avesse in mente le lacrime quando ha proposto il tema.
Mumble mumble…
Che significa matematica bisestile? Secondo il dizionario Treccani bisestile deriva dal latino bisextus, che significa “due volte sesto”, «secondo l’uso romano di contare due volte, negli anni bisestili, il 6° giorno prima delle calende di marzo (giorno bisesto), cioè il 24 febbraio». Ma quindi devo parlare di una matematica che si ripete? Se digito “matematica che si ripete” in Google, trovo: frattali, «figura geometrica che si ripete all’infinito uguale a sé stessa, su scala sempre più piccola». Sì, i frattali sono nel mio cuore da quando con la mia scuola abbiamo partecipato all’edizione del 2018 di BergamoScienza, ma… non credo sia questa la matematica bisestile.
Mumble mumble…
Digito “matematica bisestile” in Google e mi ritrovo con una serie di link per aiutarmi a capire cos’è un anno bisestile, ma non molto in merito alla matematica. Forse se cercassi in inglese… Ma come si dice “anno bisestile” in inglese? Leap year. Ma cosa significa leap? Salto! In realtà, cercando “leap year in math” trovo un paio di link interessanti: il primo è il blog Slate (che significa lavagna) dell’astronomo, divulgatore scientifico e blogger Philip Plait, Leap days explained!, e il secondo è una spiegazione matematica del sito della NASA, Leap day math. L’immagine scelta da Phil Plait in apertura di articolo è quella di una simpatica capra che salta, mentre il link della NASA porta a un breve pdf schematico ed esaustivo. Potrebbe essere sufficiente, ma…
Mumble mumble…
9 gennaio 2024: faccio un salto in libreria. Aggirarsi tra gli scaffali è, per me, rilassante e fonte di ispirazione, anche se, purtroppo o per fortuna, trovo sempre qualcosa da comprare. Non abito in una grande città e le librerie della zona sono abbastanza piccole e poco fornite per quando riguarda la parte matematico-scientifica. Se voglio avere qualche possibilità di successo, devo esplorare gli scaffali dedicati ai bambini: per i più piccoli, si trova parecchio in termine di divulgazione scientifica. Sembra che gli adulti abbiano sempre molto da spiegare ai bambini, forse perché sono ancora alla scoperta del mondo, forse perché questi sono più curiosi rispetto agli adulti. Con la scusa di regalarli ai nipoti, ho comprato un paio di testi che mi hanno ispirato. Il primo è L’atlante del tempo, di Tommaso Maiorelli, con le illustrazioni di Carla Manea: «il tempo è un’acqua profonda e misteriosa, e la Storia è lo scorrere impetuoso di quest’acqua. E allora la Storia è un fiume, con tutto quello che ci sta dentro» e gli uomini nuotano e navigano su questo fiume. In uno dei primi capitoli scopriamo che la linea del tempo non è sempre stata una linea e, mostrandoci «La linea del tempo del tempo», Maiorelli ci illustra la GEOMETRIA del tempo! Per i Babilonesi, il tempo era un ciclo senza fine, un CERCHIO, quindi, per il buddhismo, il tempo affronta «infiniti cicli eterni», per la tradizione greca e quella romana il tempo è come «una SFERA che abbraccia tutto». Maya e Aztechi elaborarono un calendario complicato, ma sostanzialmente «composto da moltissimi cicli e sotto cicli». D’altra parte, ciò che osserviamo attorno a noi ci rimanda all’idea del ciclo: «Primavera, estate, autunno, inverno e poi ancora primavera… Gli alberi nascono dai semi, crescono e prima di morire danno frutti che a loro volta daranno altri semi». È il cristianesimo a spezzare il cerchio e a cominciare a pensare al tempo come a una LINEA, una linea con un verso di percorrenza preferenziale, secondo quanto confermato dalla termodinamica. Eppure, i grandi filosofi non ci fanno mancare, nel corso dei secoli, ulteriori immagini geometriche: per Henry Bergson, «Il tempo vissuto […] è una “PALLA di neve” che ruzzolando si ingigantisce sempre di più», mentre per Hegel «la Storia avanza e si sviluppa progressivamente e il tempo “cresce” all’infinito su sé stesso, come in un vorticoso movimento a SPIRALE».
Non è solo la rappresentazione del tempo ad essere geometrica, perché anche per misurare il tempo l’uomo cerca il supporto della matematica: CERCHI di pietre celebri come quello di Stonehenge in Inghilterra non sono altro che «pesanti calendari di pietra», mentre le prime clessidre ad acqua, inventate dagli Egizi, sono costruite con vasi CONICI con un piccolo foro alla base.
La misura del tempo si affina con il tempo (!) e le unità di misura si evolvono con essa, come riportato ampiamente nel libro Quanti? Tanti! di Sandra Lucente, che esplora la matematica, la fisica, l’archeologia, la letteratura, … tutto ciò che ruota attorno alla misura e agli ordini di grandezza.
Le misure del mondo di Andrea Minoglio con le illustrazioni di Bethany Lord è il secondo acquisto: in questo libro, che permette di esercitare anche l’arte della stima, fornendo il confronto tra elementi naturali e costruzioni, ci parla del tempo usando le PROPORZIONI, visto che ci imbattiamo nella storia della Terra in 12 ore. Il riferimento al calendario cosmico ideato dall’astronomo e divulgatore statunitense Carl Sagan è evidente: «il calendario è formato da un unico anno terrestre, ma in questo arco temporale viene compressa la cronologia dell’intero universo». Se volete risparmiare tempo (!), un breve short di Erik Viotti, (conosciuto sui social come il Prof di Montagna) che usa il calendario cosmico per fare i suoi auguri a inizio anno, vi dirà tutto ciò che serve. Siccome per i più piccoli anche un anno è difficile da visualizzare (il senso del tempo cambia crescendo, dilatandosi con l’età), un intervallo di 12 ore, dalle 8:00 alle 20:00, rende meglio l’idea: la vita ha origine solo alle 9:25, ma esplode alle 18:34, i continenti si formano alle 19:31 e solo alle 19:50 si diffondono i mammiferi, e mentre i primi arnesi in pietra fanno la loro comparsa alle 19:59:27 (anche i secondi cominciano ad avere importanza!), l’uomo moderno arriva due secondi prima delle 20:00. Una linea del tempo a misura di bambino!
Il tempo corre, la scadenza incombe e la mia mente è popolata di immagini, il mio quaderno contiene solo alcuni appunti pasticciati, ma ancora non c’è il percorso che dovrebbe essere oggetto di questo articolo per il Carnevale della Matematica!
Mumble mumble…
11 gennaio 2024, ore 22:30: una lunga giornata densa di avvenimenti volge al termine, la casa è avvolta nel silenzio, la scadenza per la consegna del link è a solo una manciata di ore da me (e vorrei anche dormire un po’ nel frattempo!).
Secondo quanto riportato da Annalisa Santi in Matetango, il calendario gregoriano (attualmente in uso) entrò in vigore con la bolla pontificia di Papa Gregorio XIII Inter Gravissimas, che cancellò di fatto 10 giorni dal calendario, dal 5 al 14 ottobre 1582: da giovedì 4 ottobre, si saltò direttamente a venerdì 15 ottobre. «L'idea iniziale era di saltare i primi dieci giorni di ottobre, a cui però i francescani si opposero per poter ricordare il 400° anniversario di San Francesco, nato nel 1182. Infatti, della nascita non si conosceva il giorno preciso e si ritenne di festeggiarla nella data liturgica del 4 ottobre, giorno successivo alla morte del 3 ottobre 1226.» Presente fin dall’inizio tra i mumble mumble che hanno caratterizzato le mie riflessioni sulla matematica bisestile, c’è il libro di Abner Shimony, pubblicato nel 2000, Tibaldo e il buco nel calendario. Tibaldo Bondi è il protagonista della vicenda e, all’epoca della bolla papale, ha quasi 12 anni: per la precisione, dovrebbe compiere gli anni il 10 ottobre del 1582, uno dei giorni cancellati dalla riforma gregoriana. Per i bambini i compleanni sono una tappa importante ed è per questo motivo che Tibaldo si accanisce a cercare una soluzione. Sullo sfondo la Bologna rinascimentale, le convinzioni medico-astrologiche dell’epoca e le consuetudini in ambito ostetrico, evidenti quando il protagonista accompagna la sorella Anna Maria nell’esercizio della sua professione. Alla fine, Tibaldo troverà una soluzione, come è giusto: perché la festività di San Francesco non può essere spostata, ma il compleanno di un dodicenne può essere cancellato?
Sto divagando…
Mumble mumble…
Riprendo in mano il post di Phil Plait e lo leggo con attenzione, poi un’ultima ricerca su Google: “Numberphile leap year”, perché non è possibile che il celebre canale non abbia fatto un video dedicato. E infatti eccolo! Un video pubblicato il 28 febbraio 2012, avente per protagonista l’astronoma Meghan Gray, che parla di questo anno bisestile come di un aggiustamento. Sembra di percorrere con lei la strada della scienza, un passo avanti e uno indietro, come in una danza alla ricerca della soluzione corretta. Il nostro percorso attorno al Sole si compie in 365 giorni e… briciole! Quantifichiamo queste briciole: sono 5 ore, 48 minuti e 46 secondi, quasi 6 ore, quasi un quarto di giorno. Anche le briciole, se sono corpose, possono avere una loro sostanza (lasciatevelo dire da chi è perennemente a dieta!) e sommando quattro di questi resti otteniamo quasi un giorno intero, per la precisione 23 ore, 15 minuti e 4 secondi. Mancano ancora 44 minuti e 56 secondi per fare un giorno intero, ma questo non impedisce di aggiungere un giorno intero ogni 4 anni: il 29 febbraio! Secondo il principio per cui anche le briciole contano, se moltiplichiamo questi 44 minuti e 56 secondi per 100 (tanti sarebbero i 29 febbraio nell’arco di 400 anni), otteniamo 3.12 giorni, abbastanza per scegliere di cancellare 3 anni bisestili e così gli anni che terminano con 00 non sono bisestili, se non nel caso in cui siano divisibili per 16, come riportato dettagliatamente nella spiegazione del sito della NASA, Leap day math.
12 gennaio 2024: questo flusso di coscienza sugli anni bisestili, con qualche spruzzata di matematica qui e là, sta giungendo al termine. Non so se ho rispettato le consegne o se sono andata fuori tema, ma secondo quando riportato in Matematti, il sito di appoggio per il Carnevale della Matematica, il tema «non viene necessariamente seguito dai partecipanti». Avendo aperto con un proverbio, concludo con un modo di dire bergamasco (anche se io l’ho sentito per la prima volta da mio suocero, bresciano), giusto per chiudere il CERCHIO: «Ol tép l’è töt tecàt», che letteralmente si traduce con “il tempo è tutto unito”, ovvero «I giorni si susseguono l’uno all’altro senza soluzione di continuità».
Per me è ancora un mistero: cosa significa realmente? Certi modi di dire sono più difficili della matematica!
Carnevale della matematica #171
“Il merlo, il merlo nella luce”
(poesia gaussiana)
Benvenuti all’edizione numero 171 del Carnevale della matematica, dal tema “matematica fantasiosa”! È la prima volta che ospito il Carnevale e, devo ammetterlo, sono un po’ emozionata!
Il 171 si fattorizza 3x3x19: Dioniso, come da tradizione, ha inviato la sua cellula melodica, caratterizzata da un salto di sesta minore, come se il merlo volesse farci riflettere sull’ossimorica qualità di una luce oscura.
Oltre a essere un gioco di azione e avventura sviluppato da Betagames Group, 171 è un numero difettivo, visto che la somma dei suoi divisori è 89<171. Oltre a essere un numero palindromo nel sistema numerico decimale e nel sistema di numerazione posizionale a base 7 (333), è un numero di Harshad, cioè è divisibile per la somma delle sue cifre. È parte di ben 7 terne pitagoriche, ma sempre come cateto, ed è il diciottesimo numero triangolare, il sesto numero 13-gonale e il terzo numero 58-gonale:
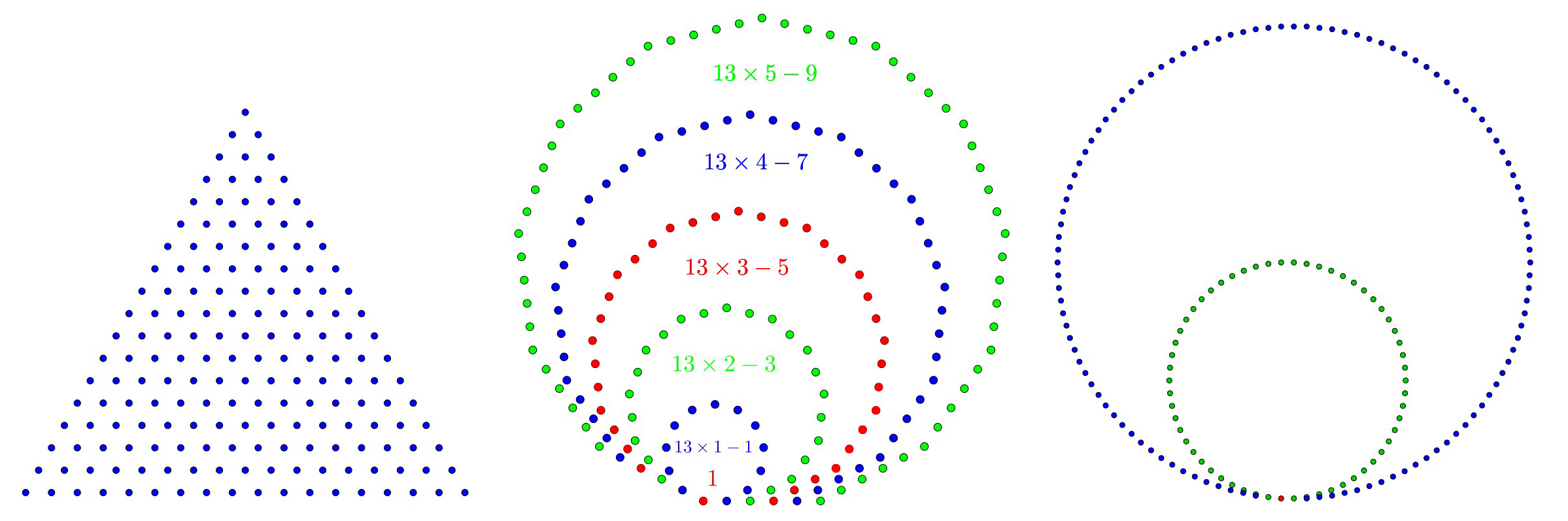
171 è anche il trentaseiesimo numero fortunato, che si ottiene con un crivello simile a quello di Eratostene:
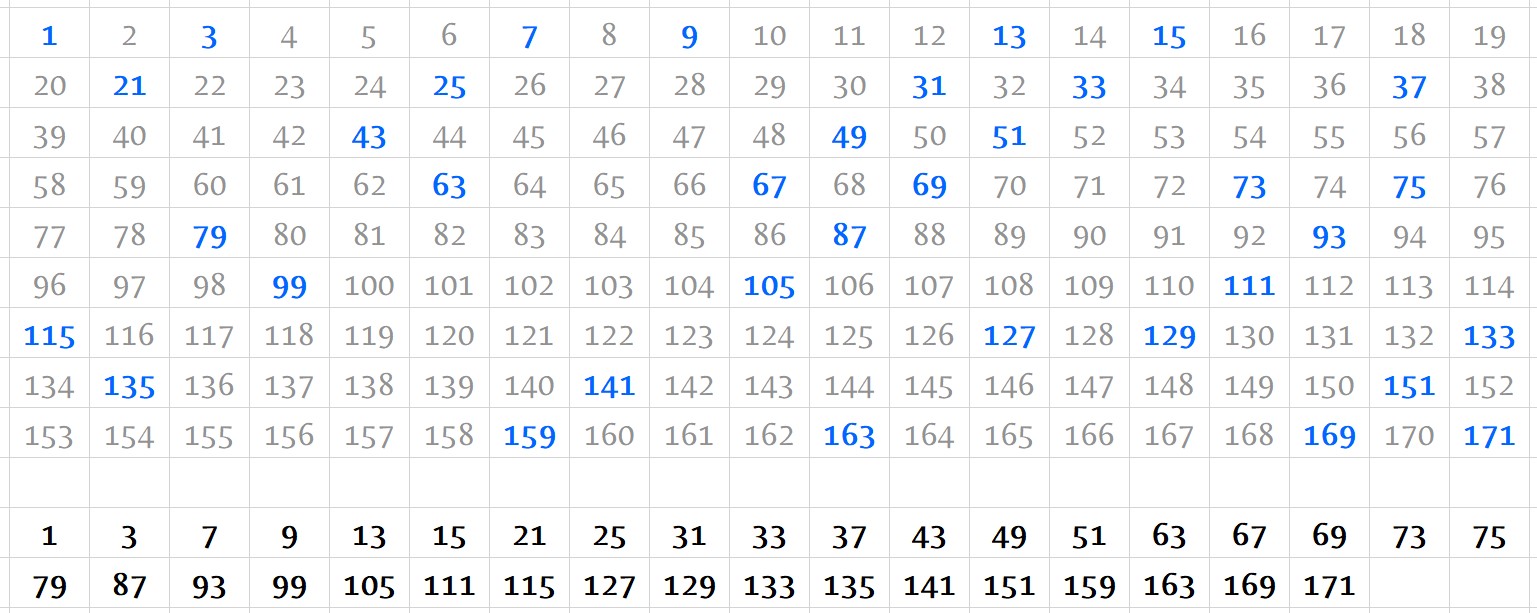
Si tiene l’1 e si tolgono tutti i secondi numeri, ovvero tutti i numeri pari. Il primo numero che si incontra a questo punto è il 3, perciò si contano due numeri e si esclude il terzo rimasto, il 5, e si procede così con 11, 17… fino a 167, nel caso della griglia che ho proposto. Oltre a 1 e 3, ora abbiamo il 7, perciò contiamo 7 numeri (sempre a partire dall’1) ed escludiamo il settimo, dal 19 fino al 165. Ora incontriamo il 9 e procediamo allo stesso modo cancellando 27, 57, 91, 121 e 153. Procedendo con la stessa regola fino a quando possibile, otteniamo la sequenza indicata.
Questi sono i contributi del carnevale:
Roberto Zanasi prosegue la rivisitazione della Divina Commedia in chiave scientifica con Inferno, Canto XIX, dove si parla di inversione di gravità e di Richard Gere poco vestito.
Dioniso continua ad esplorare il libro I paradossi di Zenone di Vincenzo Fano, che è stato uno dei punti di riferimento per il lavoro di ricerca per il suo libro, Il mistero della discesa infinita. In questa seconda parte, I contributi di Aristotele al paradosso della dicotomia, riporta una sintesi delle considerazioni di Fano relative alle interpretazioni aristoteliche del paradosso della dicotomia. In Guida veloce in città: vantaggi e svantaggi, Dioniso segnala una puntata di Radio3 Scienza, “Andavo a 30 all’ora…”, riassumendo i vantaggi e gli svantaggi in una tabellina, che potrebbe essere estremamente utile a scuola quando si parla di sicurezza stradale, applicazione della cinematica all’educazione civica.
Leonardo Petrillo propone un post dal suo blog Scienza e Musica, di carattere puramente divulgativo, adatto anche a un lettore abbastanza a digiuno di fisica e matematica, focalizzato nell’illustrare un importante modello classico della conduzione elettrica: il modello di Drude (introdotto nel 1900). Nella parte conclusiva dell’articolo, è presente un breve cenno inerente ad una rilevante verifica relativamente recente (2006) del suddetto modello, da parte di un duo di scienziati tedeschi.
Annalisa Santi ha rispolverato un post di qualche anno fa: dopo il 171 fortunato, sappiamo che in matematica si parla di Numeri Felici, Amici, Socievoli e di Numeri Fidanzati (e ci sono persino i “promessi sposi” 48 e 75), ma Ci sono i Numeri dell’Amore? Per trovare i Numeri dell’Amore è necessario uscire dalla visione matematica ed entrare in quella esoterica. E qui non si pretende certo di definire verità dimostrabili ma di sfruttare, secondo criteri assolutamente indimostrabili e soggettivi, la costanza dei numeri come dato rassicurante nel regno fluttuante dell’amore.
Piotr R. Silverbrahms, a nome dei Rudi Matematici, ha inondato la mia casella di posta elettronica di gentilezza e informazioni, spiegandomi come destreggiarmi in questo nuovo mondo. Il primo contributo è un PM, ovvero un “Paraphernalia Mathematica”, un articolo che tratta di argomenti generali – interessanti e curiosi – di matematica. È la rubrica storica della ben nota e-zine “Rudi Mathematici” (su questo sito, il loro logo è stato ospitato per 14 anni), ed è curata in persona dal fondatore, Rudy D’Alembert. Nel caso specifico, l’articolo fa parte di una piccola serie, chiamata “oltre Platone”, con evidente riferimento a superare i vincoli dei solidi platonici. È la seconda puntata della serie, e il titolo di questo episodio è Ricomincio da tre, un omaggio a Massimo Troisi e un riferimento al fatto che, pur essendo alla seconda puntata, si ricomincia a parlare di triangoli.
Il secondo contributo è un Q&D, ovvero un “Quick and dirty”, una sorta di problema dall’esposizione assai breve e dalla soluzione veloce, anche se il “dirty” specifica che magari, la soluzione, tanto veloce non è. Curve colorate parla di curve chiuse che si incrociano.
Da una rubrica all’altra, arriviamo a quello che, secondo i Rudi, è un “post istituzionale”. Oltre alla famosa e-zine, i Rudi Matematici curano una rubrica sul mensile “Le Scienze”, nella quale propongono un problema: il blog consente al gruppo di mantenere aperto il dialogo con i lettori, che hanno voglia di confrontarsi con il problema proposto e di suggerire le proprie soluzioni. L’ultimo numero di “Le Scienze”, quello di agosto, era il 660 e Il problema di agosto (660) – Mezzogiorno in comune, un problema di percorsi, anzi, di incroci.
Con poca fiducia di riuscire a rispettare i tempi (e chi segue la e-zine sa il perché), i Rudi Matematici disperavano di riuscire a pubblicare altro, ma alla fine è arrivato il 12 settembre 1900: Buon compleanno Haskell!. In questo compleanno, viene davvero celebrata la fantasia, visto che si parte dalle definizioni di Euclide e, percorrendo un sacco di antiche strade romane, si finisce nel bel mezzo della logica combinatoria.
Mauro Merlotti, autore del celebre Zibaldone Scientifico, propone due post: nel primo si parla di curve ad ampiezza costante, cioè di figure che, come il cerchio, hanno la stessa larghezza in tutte le direzioni. Abbiamo bisogno di un po’ di fantasia per capire che se le posizioniamo tra due rette parallele, possiamo farle ruotare mantenendo sempre le rette tangenti alla figura e alla stessa distanza tra loro! Il secondo è dedicato alla pizza al taglio e, dopo aver illustrato diversi modi (non convenzionali) di spartirsi una pizza, Mauro regala un po’ di pizza anche al teorema di Pitagora!
Maurizio Codogno conferma la sua fama di scrittore prolifico e ci regala una lunga serie di quizzini: quadrati alternati, molto semplice, e Vela, facile, ma funestato da una serie di errori; trapezio rettangolo, problemino geometrico facile e dall’1 al 5, una facile somma (se si sa come prenderlo); scegli la scatola è un po’ più complicato rispetto ai precedenti e ha a che fare con i codici a correzione di errore; numeri paladini ha una parte facile e una che richiede qualche conto in più, mentre numeri basici richiede un po’ di conti; il terzo maggior fattore è una semplice (?) applicazione di proprietà di fattorizzazione, primi somma e differenza di primi è molto facile; somme di numeri dispari non primi non è uno scioglilingua ma un quizzino abbastanza semplice, anche se richiede qualche conto, come pure insiemi sum-free; Doubleback Alley non è difficile, ma Maurizio ha trovato divertente ambientarlo; il sistema MIU arriva direttamente dal celebre Gödel, Escher, Bach.
Noto per le sue recensioni anche al di fuori del circuito matematico, durante l’estate Maurizio ha letto Il mistero della discesa infinita di Flavio Ubaldini, un bel romanzo “matematico” di cui si è parlato sopra; L’infinito, di Claudio Ternullo e Vincenzo Fano, che merita la fatica di affrontarne una lettura non semplice; Argomentare di Paolo Artuso, che contiene un utile ripasso della logica. Di Joseph Mazur, Maurizio ha letto Storia del tempo, ma ritiene che gli altri libri di questo autore siano migliori; con Algoritmi, monaci e mercanti di Giorgio Ausiello, si può scoprire come, nonostante tutto, nei mille anni del Medioevo anche in Europa si sia fatta matematica: poca, utilitarista, ma comunque matematica. La traduzione inglese di Arithmetical, Geometrical and Combinatorial Puzzles from Japan di Tadao Kitazawa non è il massimo, ma è interessante vedere giochi per nulla simili ai nostri soliti; Trigonometry – A very short introduction di Glen van Brummelen permette di indagare la trigonometria vista dal contesto della matematica e infine The Britannica Guide to Algebra and Trigonometry, edito da William L. Hosch, è sconsigliato, a meno di non avere curiosità storica su come questi due campi della matematica siano nati e cresciuti.
Per la serie povera matematica, troviamo Mai fidarsi dei fisici che scrivono di matematica, sulle affermazioni un po’ peculiari di Michio Kaku sulle geometrie non euclidee; Come non usare gli Invalsi ci mette in guardia: gli Invalsi mostrano differenze tra varie categorie di studenti, ma se non si specifica come sono misurati i dati, si parla sul nulla. Parlare di Invalsi porta necessariamente a domandarsi: Invalsi: Chi è che non sa leggere e far di conto? E la risposta di Maurizio è la stessa di molti di noi: i giornalisti… Scuole aperte (ma volontariamente) offre un punto di vista diverso sulle vacanze scolastiche estive, visto che segnalare il numero di settimane di sospensione delle lezioni non è statisticamente corretto. Con il post Il senatore Borghi (Aquilini) e il riscaldamento che non ci sarebbe, Maurizio commenta che il senatore Borghi scrive bene e così nasconde le proprie fallacie a proposito del riscaldamento climatico. Il 250% in meno ha attirato l’attenzione di Lucio Malan, che sa fare i conti, ma confonde l’ignoranza con la faziosità, mentre Com’è difficile spiegare ci racconta come a volte la matematica possa fare comodo per confondere un po’ le acque e arrampicarsi sugli specchi.
Per la serie matematica light, Ci sono solo sette numeri la cui radice cubica è uguale alla somma delle loro cifre è una curiosità senza reale importanza; Dati veri ma presentati male riporta la spiegazione di Giulio Betti in merito al grafico sul calo del ghiaccio artico, che è corretto ma fuorviante; Perché non fidarsi delle AI generative, parte N, ci ricorda che a una AI possiamo chiedere tante cose, ma se proviamo a farle fare un po’ di matematica sbaglia peggio di uno studente incapace.
I contributi di Maddmaths! sono come sempre numerosi e variegati:
Sulla cresta dell’onda: intervista con Roberta Bianchini, vincitrice del Premio SIMAI 2023
Roberta Bianchini è ricercatrice all’Istituto per Applicazioni del Calcolo “Mauro Picone” IAC-CNR di Roma. Nel corso del Convegno Biennale SIMAI 2023, svoltosi a Matera, ha ricevuto il Premio Biennale SIMAI 2023 “Fausto Saleri”, per la sua attività di ricerca nella matematica applicata. Il premio è rivolto a ricercatori e ricercatrici under-35. Dopo la premiazione, l’ha intervistata Marco Menale.
Conferenza pubblica di Eduardo Sáenz de Cabezón – Il video integrale
Durante il XXII Congresso UMI che si è tenuto a Pisa dal 4 al 9 settembre scorso, il famoso divulgatore matematico Eduardo Sáenz de Cabezón ha tenuto una conferenza (in inglese) dal titolo molto interessante: How to speak about mathematics to a broad audience, ora disponibile su YouTube.
Archimede 2/2023: speciale valutazione
È uscito il numero 2/2023 della rivista Archimede che è un numero speciale dedicato alla Valutazione. Vi proponiamo il sommario del direttore Roberto Natalini: “Nella continua riflessione sull’insegnamento e sull’organizzazione scolastica, un ruolo spesso trascurato è quello della valutazione. Eppure, senza valutazione è difficile capire se l’azione didattica sia stata efficace, come sia possibile migliorarla e soprattutto non renderla sempre più personalizzata. Per queste ragioni questo numero di Archimede è dedicato proprio alla valutazione, con tre contributi autorevoli e abbastanza complementari tra di loro, per ribadire la complessità della tematica. Apriamo con un articolo di Ketty Savioli, che ci presenta la valutazione “per” l’apprendimento nella scuola primaria (l’articolo è liberamente scaricabile sul sito Mondadori). Segue un articolo molto ben documentato di Rossella Garuti e Nicoletta Nolli su come funzionano e l’impatto che hanno avuto le prove INVALSI somministrate con il computer (Computer based test, CBT). Completa questa rassegna una riflessione di Roberto Ricci, presidente dell’INVALSI, sull’analisi degli apprendimenti in matematica che emerge dalle prove standardizzate. La splendida copertina e il fumetto sono dedicati alla figlia di Vito Volterra, Luisa, e aprono una breve trilogia di Alessandro Bilotta e Dario Grillotti sul matematico fondatore del Cnr che ci accompagnerà per tutto il 2023, un’appedice indispensabile alla loro graphic novel La funzione del mondo – Una storia di Vito Volterra.”
Recenti progressi su un altro problema di Erdős
I problemi posti da Erdős non finiscono mai. Recentemente c’è stato un notevole progresso su un una sua vecchia congettura sulla “densità” degli insiemi di numeri interi. Per saperne di più e capire meglio di cosa si tratta lasciamo la parola al nostro Alessandro Zaccagnini.
Riuscirà la matematica a battere il gerrymandering?
Continuiamo a parlare di gerrymandering, ovvero la pratica fraudolenta che consiste nel formare distretti elettorali in maniera partigiana, in compagnia di Nicola Apollonio.
Un incontro con László Lovász
László Lovász è un matematico ungherese e un Professore Emerito all’Università Eötvös Loránd di Budapest. È stato Presidente dell’Unione Matematica Internazionale ed è stato Presidente dell’Accademia delle Scienze Ungherese. È stato anche uno dei principali collaboratori di Paul Erdős. Raffaella Mulas lo ha intervistato nel giugno 2023, durante una visita all’Alfréd Rényi Institute of Mathematics a Budapest.
Materiali didattici sui mercati finanziari
Pubblichiamo del materiale didattico proposto in un sito web dalla Prof.ssa Rosaria Trisolino, sull’educazione finanziaria che speriamo possa essere utile al lavoro di classe nelle scuole superiori. Precede il riferimento al sito una breve introduzione della docente.
Matematica a fumetti: un nuovo librino di MaddMaths!
Negli ultimi anni sono stati pubblicati tanti fumetti a tema matematica. Con questo nuovo librino di MaddMaths! vi proponiamo una schedatura abbastanza completa di alcune opere recenti appartenenti a questa categoria. L’autrice è Gulsin Celik, studentessa dell’Università di Perugia.
Tre proposte per l’insegnamento della matematica nella scuola
Riprendiamo la discussione sul cambiamento dell’insegnamento della matematica nella scuola proponendovi alcune riflessioni e tre proposte di Giovanni Righini, professore ordinario di Ricerca Operativa presso l’Università degli Studi di Milano, da sempre attivo anche nell’ambito della didattica della matematica.
Eventi:
A Camerino torna Comunicamat – Comunicare la Matematica 2023
Comunicamat 5 – la quinta edizione del congresso “Comunicare la matematica” – ritorna con la stessa formula degli ultimi anni da mercoledì 4 a venerdì 6 ottobre 2023: 3 pomeriggi a distanza, dedicati a interventi sulla comunicazione e la divulgazione della matematica.
Incontri con la matematica n. 37 – dal 10 al 12 novembre 2023 a Castel San Pietro
Ritorna Incontri con la Matematica n.37, il tradizionale Convegno di Castel San Pietro Terme per insegnanti di Matematica, che quest’anno si svolgerà in presenza da venerdì 10 a domenica 12 novembre 2023.
Letture matematiche
“oltre Marie”: come superare gli stereotipi di genere nella scienza
Il 6 settembre esce in libreria e online “Oltre Marie”, un libro di Nastassja Cipriani e Edwige Pezzulli dedicato alle prospettive di genere in ambito scientifico. Ce ne parla Chiara de Fabritiis (Coordinatrice del Comitato Pari Opportunità dell’UMI).
Rivoluzioni matematiche: il Teorema di Eulero sui grafi
Con il numero di settembre de Le Scienze troverete in allegato il dodicesimo dei venti volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al Teorema di Eulero sui grafi ed è a cura di Alberto Saracco.
Rivoluzioni matematiche: il Teorema dei quattro colori
Con il numero di agosto de Le Scienze troverete in allegato l’undicesimo dei venti volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al Teorema dei quattro colori ed è a cura di Donatella Iacono e Sabina Milella.
Storia sconosciuta di Évariste Galois, Fabrizio Luccio e Linda Pagli
Brevi consigli per letture matematiche. “Storia sconosciuta di Évariste Galois – matematico e rivoluzionario” di Fabrizio Luccio e Linda Pagli.
L’arte della statistica, David Spiegelhalter
Brevi consigli per letture matematiche. “L’arte della statistica – Cosa ci insegnano i dati” di David Spiegelhalter, consigliato da Marco Menale.
Letture estive consigliate dalla redazione di MaddMaths!
L’estate è spesso tempo di letture ed è sempre comodo avere una lista di libri tra cui poter scegliere. Ovviamente, dati i nostri interessi, queste letture avranno uno sfondo o una motivazione matematica, a volte non troppo stretta, ma sempre presente. Altri consigli li trovate nella nostra rubrica Letture matematiche, che potete trovare a questo link. E poi non smettete dopo l’estate!
La lente matematica di Marco Menale
I criteri di Bradford Hill
I criteri di Bradoford Hill sono utilizzati negli studi statistici randomizzati per riconoscere rapporti di causalità tra grandezze. Perché correlazione non è causalità.
I modelli multiscala
Possiamo descrivere l’evoluzione di un fenomeno a più livelli. Come una lente, ci avviciniamo e ci allontaniamo per vedere dettagli e particolari. È l’approccio dei modelli multiscala. Ce ne parla Marco Menale.
Dinamica delle opinioni: i modelli cinetici
La matematica aiuta a comprendere la dinamica delle opinioni. Dalla loro diffusione, fino a persuasione e polarizzazione. Diversi modelli cinetici sono stati sviluppati negli ultimi anni. Ce ne parla Marco Menale.
È ora di dare il mio piccolo contributo a questa ricca selezione di matematica.
Ho scelto la matematica fantasiosa, perché è la matematica con la quale mi sono confrontata nel corso dell’estate. Dal 2016, l’estate è il momento per me, e per altri insegnanti della mia scuola, per dedicarsi alla progettazione dei laboratori che verranno proposti nel corso dell’imminente edizione del Festival di BergamoScienza (siamo alla sua XXI edizione e si svolgerà nella prima metà di ottobre). Il Festival ha una particolarità che lo rende unico: oltre ad offrire conferenze e incontri con famosi premi Nobel, invita le scuole a mettere a disposizione i propri alunni perché diventino divulgatori scientifici e si facciano carico di far conoscere la scienza ai bambini delle scuole degli ordini inferiori (e, a volte, ai loro coetanei). Da laureati in matematica, abbiamo sempre scelto questa come oggetto dei nostri laboratori, e direi che, negli anni, la nostra scelta si è rivelata vincente! Quest’anno abbiamo scelto la topologia e, nel corso dell’estate, mi sono dedicata… all’uncinetto! Ho realizzato nastri di Mobius e bottiglie di Klein all’uncinetto seguendo due diversi metodi, ho realizzato tori in stoffa e all’uncinetto e, infine, ho cucito dei simpatici pantaloni, seguendo il suggerimento del filmato Topology riddles, al quale sono approdata mentre cercavo materiali sull’argomento. Nel filmato (davvero bello!) si parla di questi pantaloni realizzati da due matematiche della Cornell University, Tara Holm e Lila Greco, e ho deciso di realizzarli. Sui miei pantaloni ho pubblicato anch’io due video: uno short, in cui presento il funzionamento dei pantaloni, e un video più lungo nel quale descrivo (abbastanza nel dettaglio) la realizzazione dei pantaloni, perché qualcun altro possa provare a farlo. La cosa più interessante dell’intero procedimento, a parte i miei errori da sarta dilettante, è che spendere tempo per realizzare queste creazioni mi ha permesso di riflettere sulle proprietà topologiche di questi oggetti, a un livello di consapevolezza che non sarebbe stato possibile in nessun altro modo.
Un ultimo spunto, invece, non ha nulla a che fare con la topologia, ma con i numeri figurati con i quali si è aperto questo Carnevale: in realtà, la riflessione è avvenuta in estate, è nata da un dolce che mi piace preparare, ha coinvolto mio papà, e, come sempre quando si parla con lui, i tubi!
Questo è quanto…
Direi che la rassegna offre matematica per tutti i gusti. Ci si ritrova a ottobre!
© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy









