FONTI

In base al modo in cui i partecipanti hanno avuto accesso al questionario, possiamo distinguere tre categorie:

1. 3AS: i partecipanti sono stati contattati personalmente dagli alunni della classe o dall’insegnante, tramite WhatsApp
2. Social: i partecipanti hanno avuto accesso al link condiviso sui social (Instagram e Facebook)
3. Contatti di contatti: chi ha ricevuto il questionario dagli alunni della classe ha poi contribuito a diffondere ulteriormente il questionario, inviandolo ai propri contatti

La maggior parte delle risposte (313) ci è pervenuta tramite nostri contatti diretti; le restanti risposte si suddividono quasi equamente tra social (172) e conoscenti dei nostri contatti (189).

È necessario, quindi, fare un paio di premesse:

• La nostra inesperienza nel porre le domande, combinata con l’accesso al questionario tramite i social, ha generato alcuni malintesi e alcune risposte sono, quindi, assenti o vaghe
• «Per essere attendibile, un campione deve essere rappresentativo della popolazione, ossia deve riprodurre su scala ridotta gli stessi dati rilevati per l’intera popolazione»[1]. È evidente che il nostro campione non può essere considerato rappresentativo della popolazione, visto come sono state raccolte le risposte. Evidenzieremo meglio la cosa proseguendo e confrontando i nostri dati con quelli rilevati dall’ISTAT.

GENERE ED ETÀ

Analizzando le risposte (674 in totale), abbiamo cercato di ricostruire il profilo di coloro che hanno partecipato al sondaggio, focalizzandoci sul genere, l’età e il grado di istruzione. Il 59% dei partecipanti era costituito da donne e le età sono indicate nel grafico seguente e suddivise in base al genere:

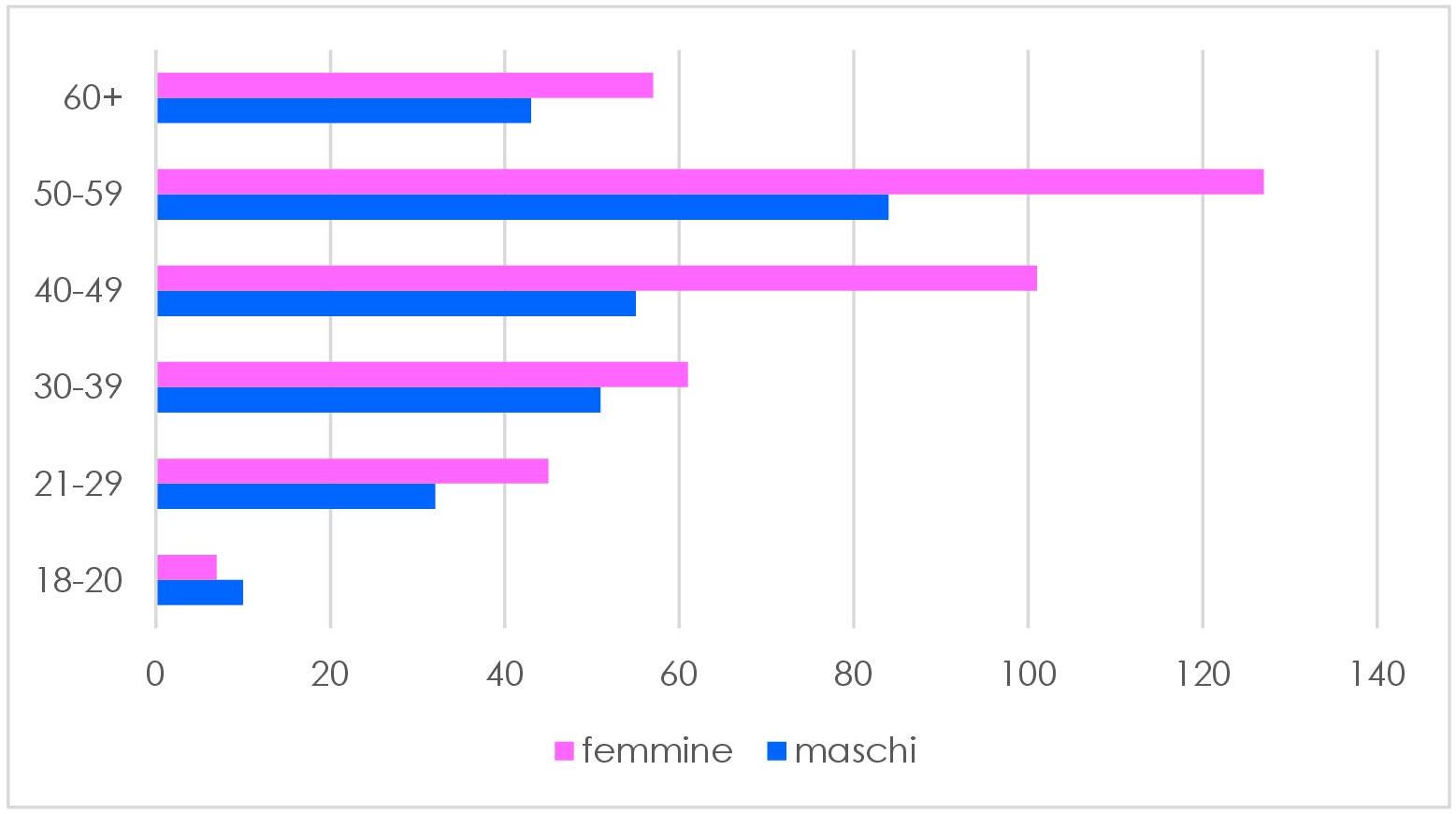
È importante riconoscere che la fascia di età 18-20 è la meno significativa, visto che hanno partecipato solo 18 persone (meno del 3%). Inoltre, visto che, per la maggior parte, i partecipanti sono ancora impegnati nella formazione, abbiamo deciso di non inserire i loro dati nei grafici successivi. La fascia più nutrita è quella dell’età compresa tra i 50 e i 59 anni (31%), nella quale è presente ancora una maggioranza femminile (127 risposte contro 84). La seconda fascia più numerosa è quella 40-49 (23%), mentre le altre tre fasce, oltre ad essere equamente distribuite per genere, hanno raccolto più o meno lo stesso numero di risposte. 

Per verificare quanto il campione fosse poco rappresentativo della popolazione italiana, almeno in termini di età, abbiamo confrontato i dati dei nostri intervistati con quelli riferiti alla popolazione residente al 1° gennaio in Italia[2].
Soffermandoci anche solo sulla percentuale dei maschi e delle femmine,

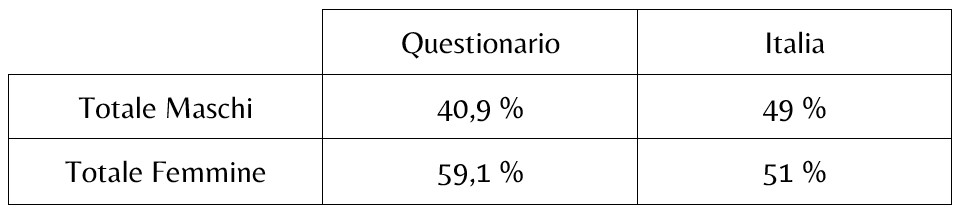
possiamo notare come la suddivisione per genere del nostro questionario non rispetti la suddivisione della popolazione italiana, dai 18 agli 85 anni.

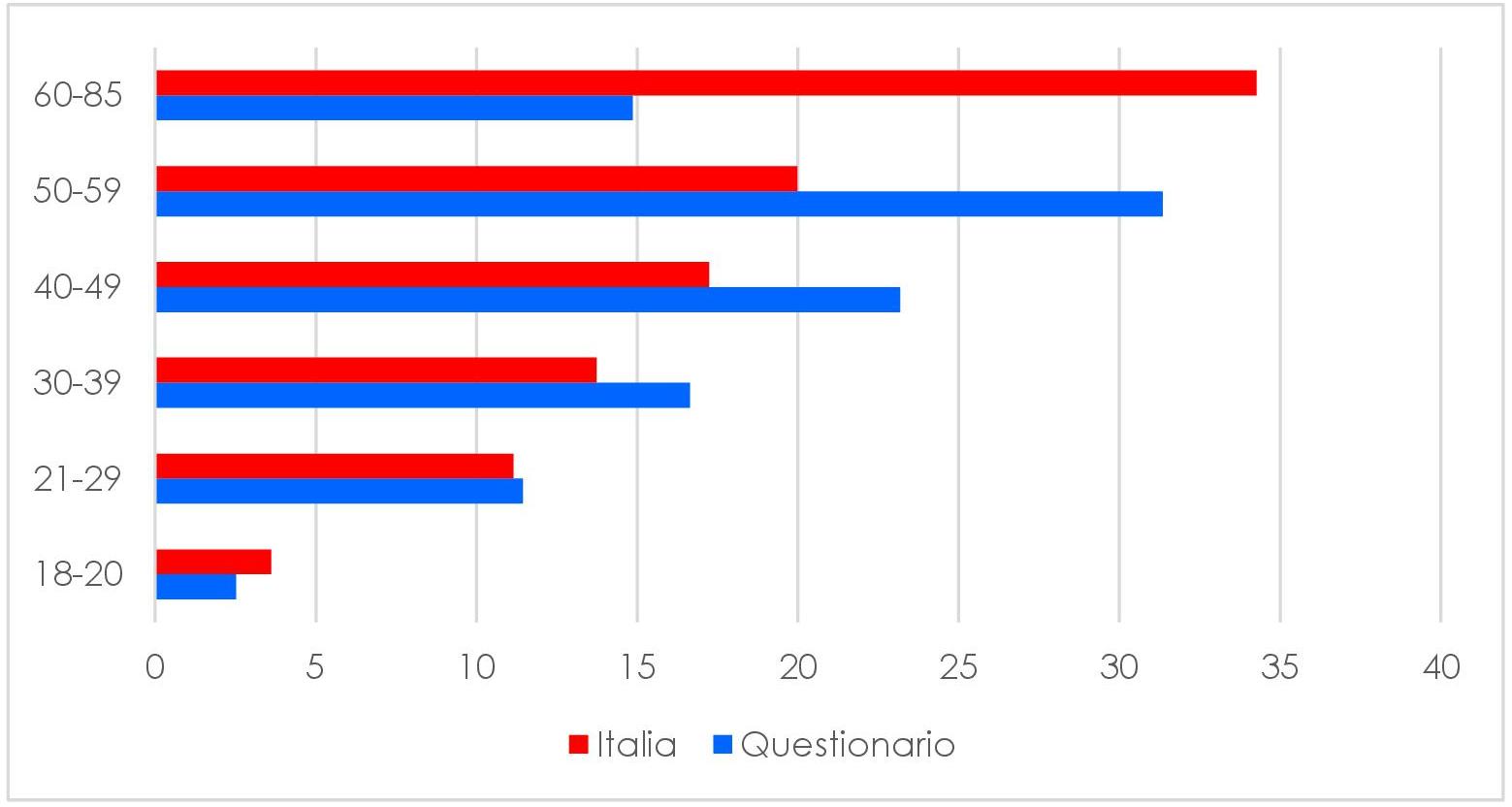
Se allarghiamo lo sguardo e consideriamo la suddivisione per età, vediamo parecchie incongruenze, ma prima è necessario precisare che la fascia di età più alta non era stata da noi definita, indicandola semplicemente come “60 e più”. Ripensando al campione intervistato, al fatto cioè che l’età più alta è quella dei nostri nonni e che oltre una certa età è più raro che accedano ai social (e quindi al questionario), abbiamo considerato come tetto gli 85 anni.

Già solo la suddivisione per età, quindi, ci restituisce il profilo di un campione che non può essere considerato rappresentativo della popolazione italiana.

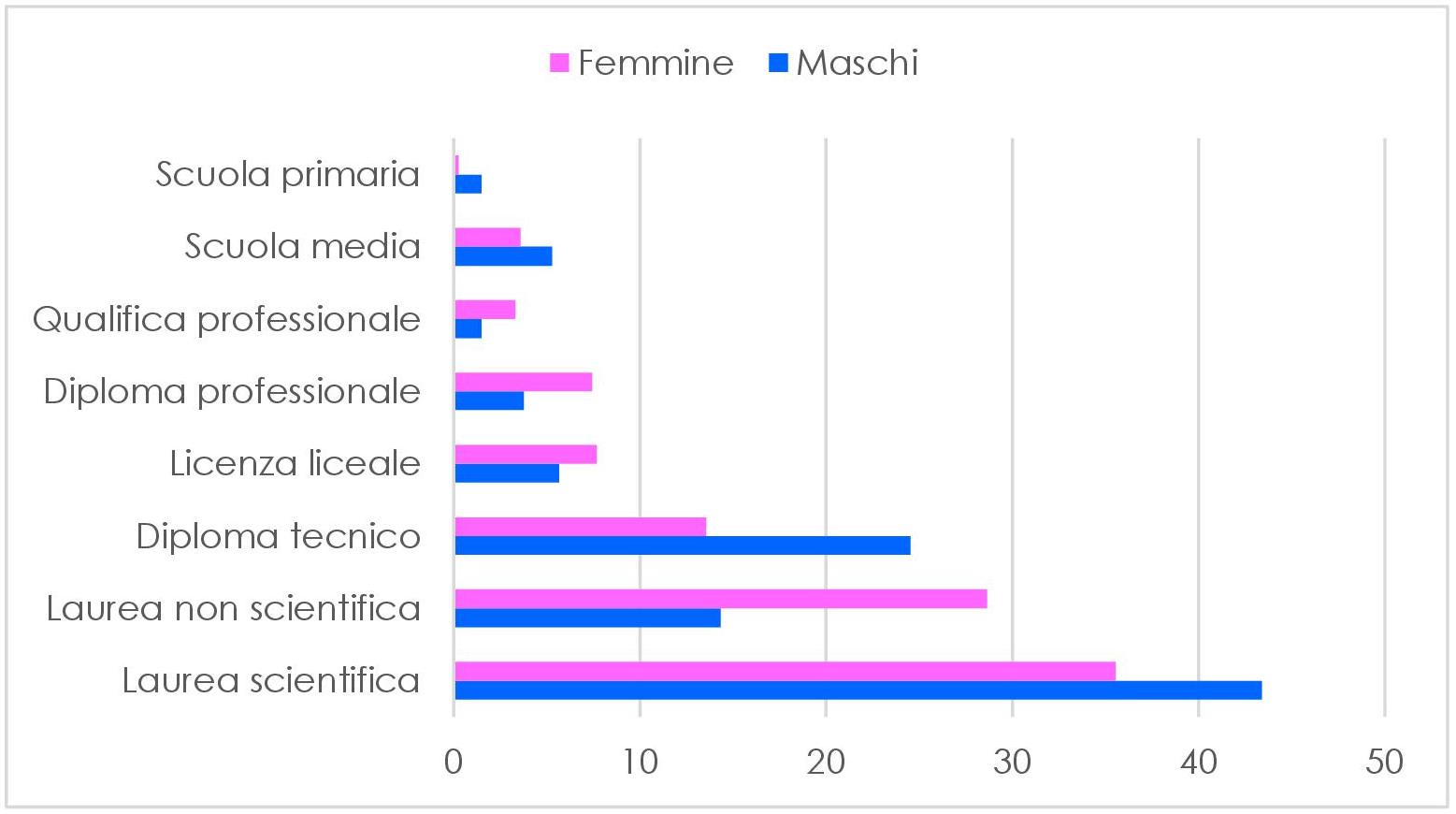
TITOLO DI STUDIO:

Dai grafici suddivisi per titolo di studio, possiamo notare una netta superiorità dei laureati, seguiti dai diplomati in materie tecniche. Possiamo notare che il numero delle licenze liceali è inferiore al numero dei diplomi tecnici, ma questo può essere dovuto al fatto che, mediamente, chi sceglie di frequentare un liceo prosegue con gli studi universitari, mentre è più probabile che un diplomato all’istituto tecnico chiuda il proprio percorso di studi dopo il diploma. Pochi sono i votanti che hanno interrotto il proprio percorso scolastico prima della scuola secondaria di secondo grado e, in genere, hanno superato i 60 anni di età, ma questo può essere dovuto al diverso obbligo scolastico: sebbene dal 1948 fosse stato imposto un ciclo di istruzione della durata di minimo otto anni, spesso la maggior parte dei bambini finiva solo la scuola primaria, nonostante le medie fossero obbligatorie. Si iniziò a frequentare obbligatoriamente la scuola media solo dal 1963, cioè per la fascia d’età che oggi è al di sotto dei 70 anni. Man mano che ci si avvicina alle fasce d’età più giovani, il grado di istruzione si innalza, grazie all’obbligo scolastico portato a 16 anni nel 2006[3]. È aumentato, inoltre, il numero di laureati, a seguito del decreto del 1999 con il quale vennero riformati i corsi di studio universitari, creando la laurea triennale e quella specialistica, e alcune professioni hanno visto un cambio di titolo di studio, basti pensare alla formazione infermieristica che, fino al 1995, è avvenuta nelle scuole regionali ed è diventato successivamente universitaria.

Quanto detto non vede differenze sostanziali nei generi, anche se i diplomi risultano essere distribuiti in maniera più omogenea tra le donne, e per gli uomini si tratta soprattutto di diplomi tecnici.

Infine, per ogni titolo di studio, abbiamo calcolato la percentuale di distribuzione in base al genere e abbiamo rilevato che:

• La scuola primaria, la scuola media, il diploma tecnico e le lauree scientifiche vedono una maggioranza maschile
• I restanti livelli di istruzione vedono una maggioranza femminile

Sembra quasi che l’ambito scientifico e tecnico siano un dominio maschile, stando al nostro campione!

[1] Bergamini, Barozzi, Trifone, Algebra.blu 1 con Statistica, Zanichelli, ISBN 9788808998828, capitolo a Introduzione alla statistica, p.a3

[2] http://dati.istat.it/Index.aspx?QueryId=42869#

[3] https://it.wikipedia.org/wiki/Storia_dell%27istruzione_in_Italia#La_scuola_nell'Italia_repubblicana

Torna all'indagine statistica

Prosegui con Matematica e mondo del lavoro

Mi capita spesso di domandarmi quanto la matematica sia presente in ambito professionale, quanto i miei (ormai ex) alunni debbano “fare i conti” con questa disciplina, tanto che al termine del percorso liceale, chiedo loro di tornare a trovarmi e di raccontarmi cosa hanno scelto di fare e quanto sia stato utile ciò che abbiamo studiato insieme. A volte sembra che il problema si esaurisca nell’utilità, ma non è così: da parte mia, c’è la necessità di capire se ho fornito loro abbastanza strumenti per affrontare il percorso professionale che hanno scelto, qualsiasi esso sia.

Confrontandomi con un medico, a settembre, mi sono sentita dire: «Diciamoci la verità: la matematica che uso nel mio lavoro è quella delle elementari: faccio le addizioni, qualche sottrazione, ma niente di veramente impegnativo!»

È stata questa la molla che ha fatto nascere in me l’esigenza di guardare più in profondità: davvero la matematica che usiamo tutti i giorni nel mondo professionale è solo quella dei primi anni delle elementari? Saltando da un pensiero all’altro, ha preso piede l’idea di realizzare un’indagine statistica e ne è nato un lavoro di educazione civica per la mia terza del liceo scientifico. Abbiamo proceduto per fasi, un po’ a tentoni: guardandomi indietro, mi rendo conto che avrei dovuto guidarli meglio, ma credo che il lavoro fatto abbia permesso loro di capire cosa significhi realizzare un’indagine statistica e, al tempo stesso, abbia fornito un’idea del mondo del lavoro un po’ più articolata. Quello che segue è l’articolo che, suddivisi a gruppi, i ragazzi hanno realizzato al termine del percorso, analizzando i risultati emersi dai questionari raccolti. Dopo aver definito gli obiettivi e i destinatari dell’indagine, gli alunni hanno partecipato attivamente alla stesura delle domande, alla scelta della modalità di somministrazione e alla correzione delle bozze; una volta approntato il modulo Google, hanno diffuso il questionario fra i propri conoscenti e, alla chiusura della consegna, hanno lavorato in gruppo, suddividendosi le domande da analizzare, realizzando una parte dell’articolo riportato di seguito e una parte del Power Point usato per presentare gli esiti dell’indagine alla classe.

In allegato:

• la presentazione che abbiamo realizzato in Power Point perché ogni gruppo potesse presentare al resto della classe il proprio lavoro
• il testo del questionario

1. Profilo dei partecipanti

2. Matematica e mondo del lavoro

3. Il rapporto con la matematica

4. Conoscenze adeguate?

5. Prospettive future

Lavoro realizzato dalla classe 3AS del Liceo Scientifico "Decio Celeri" di Lovere (Bg)
Berlinghieri Tommaso, Bonomelli Anna, Cancellerini Claudia, Cocchetti Chiara, Colosio Sofia, Elmetti Davide, Gatti Gabriele, Mazzucchelli Filippo, Meloni Claudia, Oprandi Roberta, Romele Marta, Pe Sara, Previtali Ambra, Stefini Anastasia, Stofler Riccardo, Taboni Diego, Tomaini Filippo

2 gennaio 2024: dopo essere stato fermo un turno a dicembre, il gruppo del Carnevale della Matematica viene richiamato all’ordine. Flavio Ubaldini invita i partecipanti a produrre i propri contributi, offrendo come tema la matematica bisestile.

Mumble mumble…

A me viene in mente solo “anno bisesto, anno funesto”, ma sulla stessa linea trovo “anno bisesto che passi presto”, “anno bisestile chi piange e chi stride”, ma credo che, pur parlando di matematica, Flavio non avesse in mente le lacrime quando ha proposto il tema.

Mumble mumble…

Che significa matematica bisestile? Secondo il dizionario Treccani bisestile deriva dal latino bisextus, che significa “due volte sesto”, «secondo l’uso romano di contare due volte, negli anni bisestili, il 6° giorno prima delle calende di marzo (giorno bisesto), cioè il 24 febbraio». Ma quindi devo parlare di una matematica che si ripete? Se digito “matematica che si ripete” in Google, trovo: frattali, «figura geometrica che si ripete all’infinito uguale a sé stessa, su scala sempre più piccola». Sì, i frattali sono nel mio cuore da quando con la mia scuola abbiamo partecipato all’edizione del 2018 di BergamoScienza, ma… non credo sia questa la matematica bisestile.

Mumble mumble…

Digito “matematica bisestile” in Google e mi ritrovo con una serie di link per aiutarmi a capire cos’è un anno bisestile, ma non molto in merito alla matematica. Forse se cercassi in inglese… Ma come si dice “anno bisestile” in inglese? Leap year. Ma cosa significa leap? Salto! In realtà, cercando “leap year in math” trovo un paio di link interessanti: il primo è il blog Slate (che significa lavagna) dell’astronomo, divulgatore scientifico e blogger Philip Plait, Leap days explained!, e il secondo è una spiegazione matematica del sito della NASA, Leap day math. L’immagine scelta da Phil Plait in apertura di articolo è quella di una simpatica capra che salta, mentre il link della NASA porta a un breve pdf schematico ed esaustivo. Potrebbe essere sufficiente, ma…

Mumble mumble…

9 gennaio 2024: faccio un salto in libreria. Aggirarsi tra gli scaffali è, per me, rilassante e fonte di ispirazione, anche se, purtroppo o per fortuna, trovo sempre qualcosa da comprare. Non abito in una grande città e le librerie della zona sono abbastanza piccole e poco fornite per quando riguarda la parte matematico-scientifica. Se voglio avere qualche possibilità di successo, devo esplorare gli scaffali dedicati ai bambini: per i più piccoli, si trova parecchio in termine di divulgazione scientifica. Sembra che gli adulti abbiano sempre molto da spiegare ai bambini, forse perché sono ancora alla scoperta del mondo, forse perché questi sono più curiosi rispetto agli adulti. Con la scusa di regalarli ai nipoti, ho comprato un paio di testi che mi hanno ispirato. Il primo è L’atlante del tempo, di Tommaso Maiorelli, con le illustrazioni di Carla Manea: «il tempo è un’acqua profonda e misteriosa, e la Storia è lo scorrere impetuoso di quest’acqua. E allora la Storia è un fiume, con tutto quello che ci sta dentro» e gli uomini nuotano e navigano su questo fiume. In uno dei primi capitoli scopriamo che la linea del tempo non è sempre stata una linea e, mostrandoci «La linea del tempo del tempo», Maiorelli ci illustra la GEOMETRIA del tempo! Per i Babilonesi, il tempo era un ciclo senza fine, un CERCHIO, quindi, per il buddhismo, il tempo affronta «infiniti cicli eterni», per la tradizione greca e quella romana il tempo è come «una SFERA che abbraccia tutto». Maya e Aztechi elaborarono un calendario complicato, ma sostanzialmente «composto da moltissimi cicli e sotto cicli». D’altra parte, ciò che osserviamo attorno a noi ci rimanda all’idea del ciclo: «Primavera, estate, autunno, inverno e poi ancora primavera… Gli alberi nascono dai semi, crescono e prima di morire danno frutti che a loro volta daranno altri semi». È il cristianesimo a spezzare il cerchio e a cominciare a pensare al tempo come a una LINEA, una linea con un verso di percorrenza preferenziale, secondo quanto confermato dalla termodinamica. Eppure, i grandi filosofi non ci fanno mancare, nel corso dei secoli, ulteriori immagini geometriche: per Henry Bergson, «Il tempo vissuto […] è una “PALLA di neve” che ruzzolando si ingigantisce sempre di più», mentre per Hegel «la Storia avanza e si sviluppa progressivamente e il tempo “cresce” all’infinito su sé stesso, come in un vorticoso movimento a SPIRALE».
Non è solo la rappresentazione del tempo ad essere geometrica, perché anche per misurare il tempo l’uomo cerca il supporto della matematica: CERCHI di pietre celebri come quello di Stonehenge in Inghilterra non sono altro che «pesanti calendari di pietra», mentre le prime clessidre ad acqua, inventate dagli Egizi, sono costruite con vasi CONICI con un piccolo foro alla base.
La misura del tempo si affina con il tempo (!) e le unità di misura si evolvono con essa, come riportato ampiamente nel libro Quanti? Tanti! di Sandra Lucente, che esplora la matematica, la fisica, l’archeologia, la letteratura, … tutto ciò che ruota attorno alla misura e agli ordini di grandezza.
Le misure del mondo di Andrea Minoglio con le illustrazioni di Bethany Lord è il secondo acquisto: in questo libro, che permette di esercitare anche l’arte della stima, fornendo il confronto tra elementi naturali e costruzioni, ci parla del tempo usando le PROPORZIONI, visto che ci imbattiamo nella storia della Terra in 12 ore. Il riferimento al calendario cosmico ideato dall’astronomo e divulgatore statunitense Carl Sagan è evidente: «il calendario è formato da un unico anno terrestre, ma in questo arco temporale viene compressa la cronologia dell’intero universo». Se volete risparmiare tempo (!), un breve short di Erik Viotti, (conosciuto sui social come il Prof di Montagna) che usa il calendario cosmico per fare i suoi auguri a inizio anno, vi dirà tutto ciò che serve. Siccome per i più piccoli anche un anno è difficile da visualizzare (il senso del tempo cambia crescendo, dilatandosi con l’età), un intervallo di 12 ore, dalle 8:00 alle 20:00, rende meglio l’idea: la vita ha origine solo alle 9:25, ma esplode alle 18:34, i continenti si formano alle 19:31 e solo alle 19:50 si diffondono i mammiferi, e mentre i primi arnesi in pietra fanno la loro comparsa alle 19:59:27 (anche i secondi cominciano ad avere importanza!), l’uomo moderno arriva due secondi prima delle 20:00. Una linea del tempo a misura di bambino!

Il tempo corre, la scadenza incombe e la mia mente è popolata di immagini, il mio quaderno contiene solo alcuni appunti pasticciati, ma ancora non c’è il percorso che dovrebbe essere oggetto di questo articolo per il Carnevale della Matematica!

Mumble mumble…

11 gennaio 2024, ore 22:30: una lunga giornata densa di avvenimenti volge al termine, la casa è avvolta nel silenzio, la scadenza per la consegna del link è a solo una manciata di ore da me (e vorrei anche dormire un po’ nel frattempo!).
Secondo quanto riportato da Annalisa Santi in Matetango, il calendario gregoriano (attualmente in uso) entrò in vigore con la bolla pontificia di Papa Gregorio XIII Inter Gravissimas, che cancellò di fatto 10 giorni dal calendario, dal 5 al 14 ottobre 1582: da giovedì 4 ottobre, si saltò direttamente a venerdì 15 ottobre. «L'idea iniziale era di saltare i primi dieci giorni di ottobre, a cui però i francescani si opposero per poter ricordare il 400° anniversario di San Francesco, nato nel 1182. Infatti, della nascita non si conosceva il giorno preciso e si ritenne di festeggiarla nella data liturgica del 4 ottobre, giorno successivo alla morte del 3 ottobre 1226.» Presente fin dall’inizio tra i mumble mumble che hanno caratterizzato le mie riflessioni sulla matematica bisestile, c’è il libro di Abner Shimony, pubblicato nel 2000, Tibaldo e il buco nel calendario. Tibaldo Bondi è il protagonista della vicenda e, all’epoca della bolla papale, ha quasi 12 anni: per la precisione, dovrebbe compiere gli anni il 10 ottobre del 1582, uno dei giorni cancellati dalla riforma gregoriana. Per i bambini i compleanni sono una tappa importante ed è per questo motivo che Tibaldo si accanisce a cercare una soluzione. Sullo sfondo la Bologna rinascimentale, le convinzioni medico-astrologiche dell’epoca e le consuetudini in ambito ostetrico, evidenti quando il protagonista accompagna la sorella Anna Maria nell’esercizio della sua professione. Alla fine, Tibaldo troverà una soluzione, come è giusto: perché la festività di San Francesco non può essere spostata, ma il compleanno di un dodicenne può essere cancellato?

Sto divagando…

Mumble mumble…

Riprendo in mano il post di Phil Plait e lo leggo con attenzione, poi un’ultima ricerca su Google: “Numberphile leap year”, perché non è possibile che il celebre canale non abbia fatto un video dedicato. E infatti eccolo! Un video pubblicato il 28 febbraio 2012, avente per protagonista l’astronoma Meghan Gray, che parla di questo anno bisestile come di un aggiustamento. Sembra di percorrere con lei la strada della scienza, un passo avanti e uno indietro, come in una danza alla ricerca della soluzione corretta. Il nostro percorso attorno al Sole si compie in 365 giorni e… briciole! Quantifichiamo queste briciole: sono 5 ore, 48 minuti e 46 secondi, quasi 6 ore, quasi un quarto di giorno. Anche le briciole, se sono corpose, possono avere una loro sostanza (lasciatevelo dire da chi è perennemente a dieta!) e sommando quattro di questi resti otteniamo quasi un giorno intero, per la precisione 23 ore, 15 minuti e 4 secondi. Mancano ancora 44 minuti e 56 secondi per fare un giorno intero, ma questo non impedisce di aggiungere un giorno intero ogni 4 anni: il 29 febbraio! Secondo il principio per cui anche le briciole contano, se moltiplichiamo questi 44 minuti e 56 secondi per 100 (tanti sarebbero i 29 febbraio nell’arco di 400 anni), otteniamo 3.12 giorni, abbastanza per scegliere di cancellare 3 anni bisestili e così gli anni che terminano con 00 non sono bisestili, se non nel caso in cui siano divisibili per 16, come riportato dettagliatamente nella spiegazione del sito della NASA, Leap day math.

12 gennaio 2024: questo flusso di coscienza sugli anni bisestili, con qualche spruzzata di matematica qui e là, sta giungendo al termine. Non so se ho rispettato le consegne o se sono andata fuori tema, ma secondo quando riportato in Matematti, il sito di appoggio per il Carnevale della Matematica, il tema «non viene necessariamente seguito dai partecipanti». Avendo aperto con un proverbio, concludo con un modo di dire bergamasco (anche se io l’ho sentito per la prima volta da mio suocero, bresciano), giusto per chiudere il CERCHIO: «Ol tép l’è töt tecàt», che letteralmente si traduce con “il tempo è tutto unito”, ovvero «I giorni si susseguono l’uno all’altro senza soluzione di continuità».

Per me è ancora un mistero: cosa significa realmente? Certi modi di dire sono più difficili della matematica!

Intervento al convegno Mathesis di Brescia, “Dalla ricerca alla pratica: come è cambiata la didattica della matematica”, del 19 ottobre 2023

L’intento di questo intervento è quello di parlare del ruolo che può avere il Web nella nostra didattica. È, quindi, necessario che io faccia una breve storia del Web, anche se sarà una storia un po’ egocentrica, visto che è costruita “attorno a me”. Pare, da questa foto [la foto della mia laurea, mentre stringo la mano al mitico prof. Degiovanni!],

che parta un po’ da lontano, ma non spaventatevi! È il 6 novembre del 1998, il giorno della mia laurea! Quello stesso giorno, dopo la proclamazione, sono passata in segreteria per alcune carte e ho trovato questo:

Complice il fatto che un impiego come insegnante sembrava lontanissimo, ho deciso, seduta stante, di iscrivermi a un corso biennale di perfezionamento in didattica della matematica (era venerdì, e il corso cominciava il lunedì successivo), forse per paura di perdere il mio status di studente, o per paura di crescere. La verità è che questo corso mi ha dato grandissimi stimoli e una tale ricchezza che, a distanza di 25 anni, posso ancora attingere a quanto fatto.
Nel 1998 eravamo quasi tutti digiuni di Web e, tra le materie, c’era anche informatica. Ricordo ancora la lezione nel laboratorio: la prima ricerca online sul motore di ricerca Virgilio, un po’ più noto all’epoca rispetto a Google, nato da poche settimane.

Tutti i dispositivi collegati in rete, insieme agli apparati necessari per l’interconnessione, costituiscono Internet, abbreviazione di “internetworking”, un termine che risale alla Seconda guerra mondiale e che ha a che fare con le comunicazioni radio. Come spesso capita con i grandi progressi, anche Internet è nata in tempo di guerra, durante la guerra fredda per la precisione: gli Stati Uniti d’America, negli anni Sessanta, erano alla ricerca di un nuovo sistema di difesa e di controspionaggio e Internet costituiva una facilitazione nelle comunicazioni.

Come tutti sappiamo, al CERN, sul finire degli anni Ottanta, c’era invece il problema della gestione delle informazioni: i fisici avevano bisogno di condividere i dati e Tim Berners-Lee propose una rete globale di documenti HTML. Robert Caillau, che creò il logo WWW World Wide Web, supportò entusiasticamente l’idea di Berners-Lee e creò il primo browser per Mac. Il CERN non mostrò, però, un grande entusiasmo per il loro progetto, anzi: dichiarò che si trattava di un uso improprio delle risorse e che, non rispondendo ai fini del CERN, non aveva senso spendervi del denaro. Fu così che nel 1992 Tim Berners-Lee si trasferì al MIT. Ad aprile del 1993, il CERN concesse l’uso del Web a chiunque, gratuitamente e nel 1995 gli utenti connessi erano ormai 18.000.000. Il 1995 è l’anno della nascita di quei giganti di Amazon e Ebay e, nel 2004, Tim O’Reilly parla della fine del Web statico e della nascita del Web 2.0, che vede un ruolo attivo dell’utente. Per realizzare i primi siti web, era necessaria la padronanza dell’HTML, ma ad un certo punto, chiunque, anche senza una preparazione tecnica adeguata, poteva realizzare il proprio blog e, quindi, contribuire a modellare il Web. Non solo…

Tra il 1997 e il 2000 è attivo il primo social, SIXDEGREES, ispirato alla teoria dello scrittore ungherese Frigyes Karinthy formulata in un racconto del 1929, secondo la quale ogni persona può raggiungere chiunque nel mondo con non più di sei passaggi, ovvero di cinque persone come tramite. Con i suoi 3,5 milioni di utenti, il primo social è un po’ piccolino, ma, rispetto ad oggi, sono pochi anche gli utenti della rete. Nel 2003 fa la sua comparsa Linkedin, che conta 930 milioni di utenti, nel 2004 Facebook, che ora conta 3 miliardi di utenti, e nel 2006 Twitter, con 1,3 miliardi di utenti e un logo che ricorda i simboli matematici per gli insiemi numerici.

Nel 1998, all’epoca del corso biennale, il Web era un grande ipertesto, qualcosa di più ricco e complesso di un libro, insomma, potenzialmente motivante e stimolante per gli alunni.

Questo è l’estratto di un documento scaricato da internet e stampato il 26 novembre del 1998 (o ra purtroppo irreperibile).

Il corso biennale non aveva solo l’obiettivo di darci strumenti all’avanguardia per entrare in classe, ma anche di farci riflettere sulla necessità di uno spessore culturale. La prof.ssa Maria Paola Negri (all’epoca docente di filosofia, storia e scienze dell’educazione presso l’Università Cattolica del Sacro Cuore) ha scelto di citare Einstein, che, nominando il filosofo scozzese David Hume e il fisico e filosofo austriaco Ernst Mach, ricordava come le idee nascano dai terreni più strani, purché siano fertili: «A chi mi chiede quando per la prima volta pensai alla teoria della relatività, rispondo: leggendo le opere di Hume e Mach.»

Tra le materie del corso c’era anche una riflessione sull’apprendimento, guidata dal prof. Alessandro Antonietti, attualmente preside della facoltà di Psicologia dell’Università Cattolica di Milano. Egli stimolò la riflessione di noi insegnanti sulla matematica, ci invitò a pensare che cosa questa materia rappresentasse per noi e compilammo, quindi, la nostra personale mappa della matematica: dopo aver scritto su un foglio “matematica” al centro, attorno scrivemmo tutte quelle cose che nella nostra mente si collegavano ad essa. E scoprimmo che per noi la matematica non era davvero solo una questione di numeri: gli alunni possono vederci numeri e operazioni, magari emozioni (in genere negative!), ma noi ci possiamo vedere estetica e arte, cogliamo le relazioni, e la vediamo ovunque, anche in contesti apparentemente lontani.

Il web, ad esempio, trabocca di matematica, perché funziona grazie alla matematica, ma anche perché sono numerosissimi i contenuti di matematica che possiamo trovare. Da Salvatore Aranzulla, al blog Mathone, (del centro studi A. Manzoni), attualmente ci sono parecchi elenchi di siti e basta cercare “esercizi matematica” per ottenere, in meno di mezzo secondo, oltre 15.000.000 di risultati. Ed è lo stesso risultato a cui possono accedere i nostri alunni… La situazione è cambiata completamente nel 2020, sia a livello di quantità di contenuti, sia a livello di didattica: la rivoluzione che abbiamo portato avanti, consapevolmente o meno, nelle nostre aule virtuali (più probabilmente nel salotto di casa nostra) ha cambiato tante cose e le tre icone delle principali piattaforme usate da tutti noi con la DAD non hanno certo bisogno di essere presentate.

Anche per questo, il panorama era completamente diverso nel 2006: sembra quasi di parlare della preistoria…

Dopo un corso di aggiornamento a scuola, durante il quale ci era stata presentata una piattaforma grazie alla quale condividere materiali e documenti con i ragazzi, rendendomi conto dell’impossibilità, per la mia scuola, di realizzare questa cosa così futuristica, decido, insieme a mio marito e su suggerimento di un’amica, di dare vita a un mio sito internet, con il quale, appunto, condividere materiali.

Ad agosto del 2006, il mio sito comincia il suo percorso e due sono i miei obiettivi:

• Condividere materiali con gli alunni, come appunti e schemi, verifiche ed esercizi
• Condividere cultura, attraverso recensioni di libri e curiosità

All’epoca non erano molti i siti di matematica, anzi: non erano molti i siti in generale! Ma anche gli alunni non avevano grandi possibilità tecnologiche: i miei alunni andavano in biblioteca per poter accedere al sito o per scaricare la posta elettronica, e facevano stampare le verifiche ai genitori in ufficio. Nel giugno del 2007 il primo iPhone è stato lanciato sul mercato e a partire dal 2010, questo strumento ha raggiunto anche i nostri studenti (a volte prima ancora di diventare di nostra proprietà!).

Ho deciso di presentarvi la mia personale rassegna di contenuti, che va ben al di là degli esercizi di matematica che si possono trovare online. Immaginando che ognuno di voi, a seconda dell’indirizzo in cui insegna, abbia la propria sitografia, in merito a contenuti scolastici, quello di cui voglio parlare oggi va al di là dei contenuti scolastici. Va ad incidere, appunto, sulla cultura matematica.

Comincio dall’inizio, ovvero dal febbraio del 1999, con Francesca Ortenzio, Piero Fabbri e Rodolfo Clerico, meglio noti come i Rudi Mathematici. Da febbraio del 1999 i tre amici, che lavorano totalmente a distanza, visto che abitano lontani tra loro, si occupano della pubblicazione di questa rivista elettronica, che con il proprio nome richiama i Ludi mathematici di Leon Battista Alberti e il soprannome di Rodolfo Clerico, Rudy. Il logo stesso della rivista trasuda cultura: il disegno è di Maurits Cornelis Escher e la scritta è una citazione di Pierre de Fermat e del suo celebre “Ultimo teorema”. La rivista arriva in circa 3000 caselle di posta elettronica ogni mese, tutt’altro che puntuale, ma accompagnata da una simpatica mail. Da qualche anno ha ampliato i propri orizzonti con una rubrica sul blog di Le Scienze e sulla rivista Le Scienze.

Procedo con Maurizio Codogno, che ha aperto il suo blog Notiziole di .mau. a settembre del 2001. Maurizio (che ha una voce Wikipedia tutta per lui, scritta in dialetto milanese!) è un informatico e il suo blog è una vera miniera, dato che scrive tantissimo: commenta le notizie, recensisce libri, propone giochi matematici, e, come in un diario, ci racconta ciò che fa (è così che ho scoperto di averlo incontrato nel corso dell’ultimo Festival della Fotografia che si è tenuto a Capo di Ponte). L’ultimo post è dedicato alla parabola che aiuta a fare le moltiplicazioni, scoperta al Mathematikum, il museo di Gieben.

Maurizio Codogno è anche l’ideatore e l’anima del Carnevale della matematica. Il carnevale è attivo dal 14 maggio 2008 e viene ospitato sul sito di uno dei partecipanti il 14 di ogni mese (così anche i Rudi sono obbligati ad essere puntuali!). A parte la pausa estiva, il Carnevale non si è mai interrotto ed è alla sua 172^ edizione (ospitata da Maurizio Codogno). Il carnevale ha alcune particolarità: si tratta di un gruppo di divulgatori che sceglie di pubblicare un articolo (ma spesso più di uno) attorno al tema proposto da chi ospita il carnevale. Ogni Carnevale si apre con una cellula melodica, musicata da Flavio Ubaldini, in arte Dionisoo, e scritta da Marco Fulvio Barozzi, in arte Popinga, che ha ideato la celebre poesia gaussiana: fattorizzando i numeri composti e associando a ogni numero primo un verso, è possibile ottenere una poesia.

A fine marzo 2009 fa la sua comparsa MaddMaths!, un enorme contenitore riempito da numerosi divulgatori. Nella slide ho riportato la foto di Roberto Natalini, ideatore del progetto, matematico e Direttore dell’IAC-CNR (Istituto per le Applicazioni del Calcolo “Mauro Picone”), Stefano Pisani, matematico e uno degli autori del sito satirico Lercio, Alberto Saracco, docente dell’università di Parma e “matematico prestato alla Disney”, e Marco Menale, autore della rubrica La lente matematica.

Spin off di MaddMaths! sono due podcast: il primo, Le maschere del Carnevale Matematico, è realizzato periodicamente da Fabio Quartieri, studente di matematica a Bologna, arrivato ormai al suo undicesimo episodio. Si tratta di interviste a “docenti, ricercatori, matematici che vogliono raccontare la matematica per renderla più accessibile a tutti”. È un raccoglitore di esperienze, ma soprattutto di passione.
Iheart, invece, è una serie di cinque podcast, nei quali Alfio Quarteroni racconta la matematica che ha permesso di realizzare un modello del cuore e di studiarlo meglio. Scopriamo così matematici che parlano di cardiologia e cardiologi che parlano di matematica.

Mr Palomar è un altro dei blog storici: deve il suo nome alla passione di Paolo Alessandrini per Italo Calvino. Paolo è attivo anche su YouTube e è uno scrittore molto prolifico: ha cominciato con Matematica Rock, dedicandolo alla sua passione, la musica, ha proseguito con Bestiario matematico, e l'ultimo, in ordine di tempo, è Matematica in campo, dedicato al calcio.

Taxi 1729 è una società che si occupa di comunicazione scientifica. Attivi dal 2014 con 1251 eventi all’attivo (come dichiarato sul loro sito), che spaziano tra video divulgativi, live streaming, talk spettacolo, momenti di formazione, esposizioni interattive. Gioco d’azzardo, economia e sostenibilità sono i temi che vengono affrontati. Taxi 1729 è un chiaro riferimento a Srinivasa Ramanujan, il famoso matematico indiano. Durante la sua collaborazione con Godfrey Harold Hardy, agli inizi del Novecento, ricoverato in ospedale, ha ricevuto la visita di Hardy, che non era molto abile nella chiacchiera leggera, perciò gli ha parlato di un taxi che aveva come numero 1729. E ha commentato: “Che numero insulso!” Ramanujan ha, invece, ribadito che si tratta del più piccolo intero esprimibile come somma di due cubi, ovvero 10 e 9, 12 e 1.

Victoria Hart: se vi siete imbattuti nei suoi video, non potete averli dimenticati! Sono uno più bello dell’altro: io l’ho conosciuta attraverso i suoi video sui frattali, tutti accompagnati da una chiacchiera infaticabile, mentre disegna e accompagna il disegno matematico con il canto, perché lei è una “mathmusician”, una matmusicista. Figlia di due matematici, ha scoperto la sua passione a 13 anni e ha scelto di coltivarla in modo davvero originale.

Nel 2011, Google commissionò la creazione di 100 canali YouTube per aumentare il traffico sulla piattaforma, che aveva acquistato nel 2006 (e che era nata nel 2005). Per la matematica venne coinvolto Brady Haran e lui scelse di raccogliere la sfida. Per il nome, scelse di proposito di evitare il termine matematica, per minimizzare il riferimento alla scuola, ma la scelta cadde su un termine che richiama l’amore per i numeri, un canale “filonumerico” potremmo dire, Numberphile. Ci sono video di tutti i tipi, da Cédric Villani che parla delle medaglie Fields, a Tadashi Tokieda che fa vedere un cerchio che passa attraverso un buco quadrato, che ha la diagonale minore del diametro del cerchio, o Cliff Stoll che parla delle sue mille bottiglie di Klein nascoste nel seminterrato di casa sua. E c’è pure un video bellissimo, dedicato a pi greco, lungo, ovviamente, 6 minuti e 28 (un chiaro rimando a 2pi), con il quale gli autori mostrano la realizzazione di un miglio di pi greco, con un milione di cifre di pi greco.

Il MATH-segnale è un canale assolutamente da seguire: Davide Calza e Riccardo Moschetti hanno una preparazione fuori dal comune, una grande simpatia e un’abilità grafica che rendono molto facile seguire anche i contenuti più complessi. Ci sono alcuni video che sono imperdibili, come i due dedicati ai grafi, uno per giocare a guardie e ladri e l’altro per trattare la divisibilità in un modo diverso dal solito. Poi ci sono i video realizzati sulla spinta di scoperte recenti, come la nuova dimostrazione del Teorema di Pitagora ad opera delle due studentesse statunitensi: Davide e Riccardo hanno spiegato con chiarezza e senza risparmiarci alcun passaggio, in modo da guidarci sani e salvi alla meta.

Non potevo non concludere con Ilaria Fanelli, autrice del canale IlariaF Math: il suo entusiasmo e la sua passione sono trascinanti, perché con le sue idee Ilaria coinvolge un sacco di persone, non lavora da sola. Così abbiamo gli shorts “Che cosa è per te la matematica?”, che ha realizzato durante Strambinaria, ma che di fatto aveva già cominciato a coltivare tempo fa, quando apriva le sue serate, intervistando divulgatori matematici e non solo, proprio con questa domanda. Troviamo la risposta dei Rudi Mathematici, quella della matematica Roberta Fulci, redattrice e conduttrice di Radio3Scienza, finalista del premio Science Book of the Year con “Il male detto”, quella entusiasta di Federico Benuzzi, e, ultima in ordine di tempo, la risposta meno entusiasta di Federica Gerini, laureata in Biologia della Conservazione, che lavora nell’ambito della comunicazione per Musei e associazioni di protezione della Natura: ha definito la matematica un incubo! Altro grande lavoro di Ilaria, che è un vero catalizzatore di passione, è la sfida #peopleformath Ci sono già state due edizioni e l’elenco dei matematici raccontati dai vari divulgatori sta diventando importante. Ma Ilaria lavora anche parecchio alla divulgazione: sul suo canale si trovano video per giocare e video per approfondire, come la serie dedicata a Dante e la matematica.

Nel post Che cos'è Maddmaths! possiamo leggere: «La matematica è un po’ la bestia nera di tutti gli studenti e non ha una buona reputazione presso il cittadino medio, nonostante gli sforzi, spesso eroici, di alcuni insegnanti validi e preparati che cercano di presentare questa materia in un modo più vivo e attraente. [...] Per questo, a partire dal 2008, nell’ambito delle iniziative della SIMAI (Società Italiana di Matematica Applicata e Industriale) abbiamo cercato di immaginare un percorso che contribuisse a cambiare questo stato di cose, perché crediamo che la matematica sia oggi una delle risorse principali della tanto decantata innovazione tecnologica e per questo sia necessario rimuovere i pregiudizi esistenti contro questa disciplina.»
Ilaria Fanelli dichiara, nella sua home: «Le motivazioni che mi hanno spinto sono molteplici: in primis la volontà di mostrare il lato curioso e affascinante della matematica agli appassionati e ai non addetti ai lavori, offrire agli insegnanti spunti didattici e divulgativi da utilizzare nelle proprie classi e creare una community di persone che possano collaborare tra loro anche a distanza.»

La mia homepage, all’inizio di questa avventura, riportava questo messaggio di benvenuto: «Come tanti altri insegnanti di matematica, ho deciso di “creare” il mio sito internet per poter fornire appunti, esercizi, notizie, curiosità… agli alunni interessati e volenterosi. La domanda sorge spontanea: l’insegnante di matematica medio è realmente convinto che i suoi alunni siano interessati ad una materia così ostica e difficile e, di conseguenza, così odiata? Forse non si tratta di convinzione: forse è l’ingenuo tentativo di far conoscere aspetti inconsueti e divertenti di una materia spesso odiata. Il mio tentativo si esprime già dal titolo del sito: AMO LA MATEMATICA! E di fronte ad un’affermazione del genere, scommetto che a qualcuno di voi sta già venendo l’orticaria…»

Il titolo del sito, negli anni, mi ha regalato piacevoli siparietti: quando fornisco il mio indirizzo email, Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo., do il via a commenti di tutti i tipi, dal (purtroppo) tipico “Ho sempre odiato la matematica” al più simpatico “Mi è sempre piaciuta, ma poi ho preso altre strade”. Ma anche quando mi viene raccontato l’odio per la matematica, è un sentimento venato di rimpianto, che potrebbe essere ben espresso dalle parole di Mickaël Launay (che campeggiano ora nella mia homepage): «Non la amiamo, eppure ci piacerebbe amarla».

C’è da dire che, da quando esiste, il mio sito ha obbligato i miei studenti a dire, almeno una volta, “Amo la matematica”, oppure, per usare un’espressione dialettale (tipica sia del dialetto bresciano che di quello bergamasco – per onorare le capitali della cultura 2023): “Amò la matematica?!”, che non è il passato remoto del verbo amare, ma “Ancora la matematica?!”, come a dire: Ci hai stancato! Ne abbiamo abbastanza!