Articoli (58)
Conferenza senza bordi: Topologia è…
Pc collegato al proiettore, sullo schermo è aperto un file Power Point con una bella copertina: sullo sfondo immagini di topologia, in evidenza la scritta: “Conferenza senza bordi: Topologia è…” e la data.
Il tavolo con il pc è invaso da oggetti topologici
Sale sul palco la Prof1:
Prof1: Buonasera a tutti e benvenuti! Siamo qui, questa sera, per parlarvi di topologia, l’argomento dei nostri laboratori di BergamoScienza. Purtroppo, hanno chiesto a me di parlarvene, ma io all’Università non ho sostenuto l’esame di topologia. Perciò (la diapositiva successiva recita: “Grazie per l’attenzione!”), vi saluto e vi ringrazio per aver partecipato.
Scende dal palco e se ne va.
Il palco resta vuoto.
Attimo di silenzio.
Dubbi.
Perplessità.
La Prof2, alzandosi dalla prima fila, prende la parola:
Prof2: Scusate! Temo che ci sia stato un piccolo malinteso con la Prof1. Non erano questi i patti…
Proverò a dire qualcosa io della topologia, anche se ne ho un pessimo ricordo dall’università: il professore mi ha bocciato per due anni consecutivi a tutte le sessioni e non ho imparato nulla. Ci provo!
La Prof2 sale sul palco, mentre qualcuno si avvicina al pc e cambia la presentazione, inserendo una nuova chiavetta:
Comincerei dallo spiegarvi cosa significa “conferenza senza bordi”. La topologia è una parte un po’ originale della matematica, tanto che viene chiamata “geometria del foglio di gomma”. Io comincerei con questi due anelli: dal posto non li vedete molto bene, perciò, inviterei qualcuno di voi sul palco a darmi una mano (Prof2 chiama Alunn01, prende dal tavolo la striscia di carta e gliela passa, poi confabula con Alunn01, fingendo di spiegare cosa deve fare). Prendete una striscia di carta: se incollate gli estremi tra di loro, ottenete un cilindro e, come potete vedere (Alunn01 mostra la cosa avvicinando i due estremi) ha una superficie interna e una esterna. Adesso, incolliamolo facendo fare una torsione di 180° a uno dei due estremi (Alunn01, intanto, collega con la cucitrice i due estremi): quello che otteniamo è un nastro di Mobius, un nastro che NON ha un dentro e un fuori, perché ha un’unica superficie. Ora prendiamo una seconda striscia e realizziamone un altro, ruotando l’estremo in senso opposto (Alunn01 procede e vengono mostrati i due nastri. Prof2 prende dal tavolo due fogli bianchi) Se prendo due fogli bianchi qualsiasi, di forma rettangolare, riconosciamo tutti che hanno quattro lati [1]: se li uniamo lungo un lato, entrambi i fogli perdono un lato, ma se uniamo due nastri di Mobius… beh! Ogni nastro di Mobius ha un solo lato quindi se io unisco due nastri lungo l’unico lato che hanno… ottengo una bottiglia di Klein che è una bottiglia speciale, visto che non ha bordi, non ha dentro e fuori e non si può riempire. Ecco il motivo per cui questa sarà una conferenza senza bordi, perché non ci sarà qualcuno che parla e qualcuno che ascolta, ma chiunque potrà intervenire, se ha qualche curiosità o se vuole dire qualcosa sulla topologia.
Entra Alunn02 e prende la parola:
Alunn02: Direi che è ora di mostrare realmente come si svolgerà questa conferenza e cos’è la topologia. Comincerei con una sfilata del Topo-outfit, la linea di moda alla quale abbiamo lavorato quest’anno: Alunn03, tocca a te!
Alunn03 entra con i pantaloni, sul lato arancio, un toro rosso in testa e il nastro di Mobius enorme a tracolla, una bottiglia di Klein all’uncinetto in una mano come una borsetta e al polso un nastro di Mobius come bracciale
Alunn02: Come vedete, Alunn03 indossa degli originalissimi pantaloni topologici. Ma in cosa consiste la loro originalità? Non solo nel colore, non certo nella forma (Alunn03 allarga i pantaloni per mostrarne la grandezza), ma nel fatto che, se io chiedo a Alunn03 di mettere a rovescio i pantaloni, lo può fare anche in pubblico, perché non ha bisogno di toglierli! Prego, Alunn03! [2]
Alunn03 procede a rovesciare i pantaloni mentre Alunn02 lo accompagna: A molti di voi sarà capitato di macchiare i pantaloni e di non avere la possibilità di cambiarli. Questa potrebbe essere la soluzione! Mettendoli a rovescio, anche la macchia verrà nascosta! Come vedete, si tratta di un capo molto originale, realizzato con una, anzi due stoffe morbide ed elastiche, in modo che possa essere indossato da chiunque. Certo, per poter rovesciare i pantaloni bisogna essere un po’ elastici e…
Entra Prof3, con dei libri sotto il braccio, vestito come un professore serio. Interrompe Alunn02 e comincia a parlare:
Prof3: Non è possibile! Ma voi davvero pensate di poter parlare di topologia in questo modo? Andatevene, per favore (e caccia i due dal palco), qui la gente vuole ascoltare qualcosa di serio. Sarà meglio che prenda in mano io la situazione. Buonasera, mi presento: sono Prof3, ex studente del Celeri, e laureando in fisica delle interazioni fondamentali all’Università degli studi di Padova. (si avvicina a pc per mettere una chiavetta e far partire una presentazione e anche chi aveva la postazione a pc si allontana preoccupato). La nobile branca della topologia serve per capire i segreti del nostro universo, dalle cose più grandi come gli astri e le galassie alle cose più piccole come le particelle subatomiche. Prendiamo due buchi neri, oggetti così pesanti che la loro gravità attrae a sé qualsiasi cosa, perfino la luce. Se sono abbastanza vicini, finiranno per fondersi in un solo grande buco nero. Ed ecco che finalmente la forma che volgarmente hanno chiamato “pantaloni” ora ha un significato scientifico importante! Ma non è finita qua: se leggiamo questa figura al contrario, il modello standard, e volendo anche le teorie più recenti e straordinarie come la teoria delle stringhe, ci dicono che questa figura rappresenta una particella che a un certo punto si divide in due particelle più piccole. E questi fenomeni servono non solo alla fisica, ma alla medicina, all’ingegneria e a tutte le scienze! E potrei andare avanti con altri mille esempi, come lo spin delle particelle paragonato al nastro di Moebius, oppure…
Mentre Prof3 sta concludendo, entra Alunn04, portando un vassoio, sul quale sono presenti una tazza, una teiera e una ciambella. Alunn04 prima offre la tazza vuota a Prof3 (che si ferma perplesso in mezzo a una frase) e poi comincia a versare del liquido nella ciambella, al che Prof3 la ferma: [mentre avviene questo scambio, chi era a pc torna in postazione e fa partire la slide successiva della prima presentazione]
Prof3: Ma cosa stai facendo?
Alunn04: Beh, voi topologi non dite forse che una tazza e una ciambella sono la stessa cosa? Stavo versando il tè nella ciambella e le stavo dando la tazza da mangiare…
Entra allegra Alunn05 portando con sé una palla pelosa:
Alunn05: Se si parla dell’umorismo dei topologi, allora tocca a me! Sono qui per parlarvi del teorema della palla pelosa, dimostrato dal matematico olandese Brouwer nel 1912! (nel frattempo, Prof3 se ne va mostrando esasperazione e Alunn04 abbandona il palco) «Il teorema ci dice che, se abbiamo una palla pelosa come questa, non è possibile pettinarla in modo continuo in una stessa direzione, senza che ci siano peli che vanno nella direzione sbagliata o punti non pettinati come questo punto qua. Questo teorema […] può essere applicato anche al nostro pianeta, infatti possiamo considerare, anziché la direzione dei peli, la direzione del vento e il teorema in questo caso ci dice che sulla Terra esiste sempre un punto, come questo qua, in cui non c’è minimamente vento.» [3]
Entra, chiaramente infastidito, il Prof4, vestito da serioso professore e prende la parola:
Prof4: Ma non è possibile! Non si può parlare della matematica in questo modo, come se si trattasse di una barzelletta da raccontare! (Caccia Alunn05dal palco) Innanzi tutto, scusa collega (rivolgendosi alla Prof2), mi pare che tu sia stata un po’ imprecisa su quella cosa del “senza bordi” (sarcasticamente). Forse è bene che chiarisca il concetto per il nostro pubblico. Ho giusto predisposto un paio di slide in proposito... (fa un cenno e subito vengono proiettate le foto delle dispense di topologia, in cui viene “descritto” come ottenere cilindro, nastro di Möbius, toro e bottiglia di Klein a partire da un quadrato). Partiamo considerando un quadrato, o un rettangolo, tanto sono spazi topologici omeomorfi. Come si evince chiaramente dalle immagini mostrate, è possibile quozientare il quadrato chiuso, ovvero [0,1]×[0,1], mediante relazioni di equivalenza opportunamente definite, per ottenere altri spazi topologici: ad esempio, se definiamo la relazione di equivalenza ρ mediante la partizione formata, per ogni punto Y di un lato verticale, dalle coppie {Y,Y^'}, con Y' simmetrico di Y rispetto all’asse di simmetria verticale, e dai singleton {X} per ogni altro punto X del quadrato, lo spazio quoziente [0,1]^2/ρ è omeomorfo al cilindro, cioè S^1×[0,1]. Il cilindro non risolve tuttavia la questione del togliere i bordi, dato che ha frontiera omeomorfa all’unione di due circonferenze distinte, come neppure il nastro di Möbius, dove il bordo è evidentemente omeomorfo a S^1 (sguardo di rimprovero alla Prof2)... se però consideriamo la naturale relazione di equivalenza che identifica anche i lati orizzontali, ciascuno percorso nel verso positivo, allora il quoziente che si ottiene è chiaramente omeomorfo a un toro, cioè al prodotto cartesiano della 1-sfera con se stessa, che ha frontiera topologica vuota, anche senza scomodare la bottiglia di Klein, che pure in effetti è un quoziente del quadrato, mediante la relazione...
Alunn01, dal posto, alza la mano e, togliendogli la parola, esclama: Io non ho capito niente, me lo può rispiegare?
Si alza dal pubblico la Prof5 e cerca di risolvere la questione
Prof5: Prof4, se non è un problema, provo io. (Rivolgendosi al pubblico) Prendiamo un rettangolo (o un quadrato, visto che per la topologia sono la stessa cosa) e ripieghiamolo su sé stesso. (procede a realizzare davvero quanto dichiarato, con un foglio rettangolare) Come vedete, otteniamo un cilindro. Ora ripieghiamolo di nuovo e facciamo combaciare i due estremi: quello che otteniamo è un toro, quello che i non matematici chiamano ciambella. (prendendo in mano un mega-toro realizzato con la stoffa) Eccone qui una versione in stoffa, un po’ più grande per rendere l’idea! In ogni caso, avrete notato che da un foglio con quattro bordi, siamo passati a un oggetto che non ha alcun bordo!
Prof4: (impaziente) Va bene… immagino che forse così possa essere chiaro, per un pubblico non esperto.
Prof5: Volevo concludere raccontando che recentemente è stato dimostrato un risultato di topologia molto importante, che era stato enunciato nel 1977, perciò ci sono voluti quasi cinquant’anni e…
Interviene Alunn06, timidamente, salendo sul palco con in mano il nastro di Moebius che è una riproduzione all’uncinetto del celebre nastro di Escher:
Alunn06: Mi scusi, Prof5, credo che ora tocchi a me, visto che lei sta parlando da un po’. (Rivolgendosi al pubblico) Vorrei mostrarvi questo bellissimo nastro di Mobius, realizzato a uncinetto seguendo il disegno di Escher, che tutti, credo, conosciamo (alle spalle compare l’immagine del dipinto di Escher). La cosa interessante di questo nastro è che non è il classico nastro di Moebius: se notate, è arrotolato su sé stesso ben due volte e…
Entra, prepotentemente, Alunn07:
Alunn07: Ma cosa c’entra adesso il liceo artistico? Stiamo parlando di matematica e tirate fuori queste cose artistiche. Io direi che è ora di cominciare a fare i seri. Sapete, i matematici vedono sé stessi come dei poeti sognatori, mentre gli scienziati usano la matematica come uno strumento, utile per ottenere un risultato. La verità è che hanno ragione tutti! Pensiamo alla teoria dei nodi, che è una branca della topologia: questa parte è nata per risolvere un problema scientifico. Prima della scoperta degli atomi, alcuni scienziati, tra i quali Lord Kelvin, credevano che la materia, chiamata etere, fosse fatta di nodi e garbugli. Quindi, hanno cominciato a classificare i singoli nodi (alle spalle compare l’immagine della tavola dei nodi), per poi rendersi conto che non era un modello adeguato. Allora hanno perso interesse, conquistati dalla nuova teoria degli atomi, che era effettivamente quella corretta. I matematici, però, persone un po’ strane come avrete capito, trovarono nei nodi un simpatico passatempo e continuarono a sviluppare questa teoria, che sembrava non avere alcuna utilità. [4] La scienza, inaspettatamente, ad un certo punto ha avuto bisogno di questa teoria, perché… perché… forse è meglio che lasci la parola alla Prof6, docente di scienze del nostro istituto, che potrà spiegarci cosa intendo. (Invita a salire sul palco la Prof6).
La Prof6 sale sul palco e comincia a parlare:
Prof6: Se ci venisse chiesto di disegnare il DNA molti di noi disegnerebbero una scala a chiocciola, la famosa doppia elica. Gruppi alternati di fosfati e di zuccheri sono il corrimano della scala, mentre le coppie delle quattro basi complementari, adenina, timina e citosina, guanina, formano i gradini della scala.
La struttura di basi si chiama struttura primaria, la doppia elica, invece, struttura secondaria.
La lunghezza del DNA si misura in termini di coppie di basi: il DNA umano è lungo circa 3 miliardi di coppie, quello del batterio più comune, l'Escherichia Coli, solo 4,4 milioni di basi.
Nel 1981 grazie ad una tecnica chiamata elettroforesi si giunse alla conclusione che la lunga molecola del DNA ha anche una struttura terziaria, che consiste in un ulteriore avvitamento nello spazio, un po’ come il filo della cornetta del telefono che dopo un lungo utilizzo, assume una struttura super-inanellata, aggrovigliandosi su sé stesso. Quindi il DNA, nel nucleo della cellula, si trova tutto aggrovigliato e compattato in uno spazio piccolissimo e, in alcuni casi, addirittura sotto forma di anello. In queste condizioni, può capitare che si formino nodi, pieghe e intrecci che hanno ripercussioni anche molto negative sulla funzionalità della cellula. (Al lato del palco si mettono Alunn04 e Alunn05: Alunn04 si siede sull’angolo del palco e Alunn05 prima prende le due trecce e le avvolge a elica, poi le compatta creando una specie di chignon. Prof6 fa un cenno affermativo) Infatti, durante la replicazione e la trascrizione, la doppia elica si deve aprire per permettere l’accesso agli enzimi. Separare due semi-eliche che sono super inanellate, talvolta addirittura formando uno o più nodi, è un problema molto complesso oltre che molto interessante. (A questo punto Alunn05 disfa una treccia ad Alunn04, poi cerca di pettinarla, ma sembra che trovi davvero un sacco di nodi… è peggio di una palla pelosa!) Esistono degli enzimi in grado di sciogliere gli eventuali nodi del DNA e riportare la doppia elica a una configurazione più stabile, questi enzimi sono chiamati topoisomerasi. Ed è proprio qui che entra in gioco la teoria dei nodi; infatti, grazie ad essa e alla topologia si possono creare dei modelli con cui validare o smentire ipotesi su come funzionano le topoisomerasi. [5]
Al termine della presentazione della Prof6, interviene Alunn06:
Alunn06: Mi scusi, professoressa, posso aggiungere una cosa? Vorrei dire che i nodi non sono proprietà solo della scienza, ma anche dell’arte. A me, parlando di nodi, vengono in mente gli anelli di Borromeo (sullo sfondo si apre l’immagine di un nodo borromeo): sono «un esempio di link con tre componenti, ciascuna delle quali è un nodo banale (cioè un anello semplice) e “link borromeo” (più erroneamente ma comunemente detto “nodo borromeo”) deve il suo nome proprio al simbolo araldico fatto risalire alla persona di Federico Borromeo, cardinale e arcivescovo di Milano, che lo scelse appunto come suo emblema, simbolo della dinastia borromea e, data la sua religiosità, i tre anelli potrebbero rappresentare anche la trinità cristiana.» [6] Realizzarlo è molto semplice: basta prendere due anelli disgiunti e poi legarli con un terzo anello (prende due anelli già realizzati e li collega grazie al terzo anello, una striscia di carta fissata con la cucitrice) È così bello che è stato scelto come logo dall’Unione Matematica Internazionale.
Dal pubblico si alza Alunn08:
Alunn08: Be’, se si vuole parlare di nodi nell’arte, direi che tocca a me… Anzi: tocca a Leonardo da Vinci! Forse può sembrarvi strano questo riferimento al genio di Leonardo in una conferenza sulla topologia, ma si tratta, appunto, di un genio e possiamo trovare qualche traccia di topologia anche nelle sue opere. La mostra che abbiamo presentato ai ragazzi durante il Festival è stata arricchita dalla cornice della biblioteca: con le finestre chiuse, in penombra o con l'illuminazione artificiale, abbiamo ricreato una bolla fuori dal tempo, sia per preservare i libri ivi conservati, sia per poter ricreare un percorso che si sviluppa attraverso i secoli.
Artista, inventore, scienziato… non è così facile definire Leonardo da Vinci, non possiamo incasellarlo o mettergli un’etichetta. Nato nel 1452, Leonardo fa il suo ingresso nella bottega di Andrea del Verrocchio da adolescente: il Verrocchio è un grande artista, ma anche un grande maestro, capace di insegnare ai propri allievi l’uso delle più diverse tecniche pittoriche dell’epoca. Secondo la leggenda, Verrocchio rimase così impressionato dal talento di Leonardo da rinunciare alla pittura per il resto della sua vita, sconfitto dal confronto con l'allievo.
Leonardo si definiva un “homo sanza lettere”: aveva un padre notaio, ma si era rifiutato di seguire le sue orme ed era stato il nonno probabilmente a trovargli il posto presso la bottega del Verrocchio. La sua curiosità insaziabile lo porta a studiare, tanto da costruirsi, nel corso della sua vita, una biblioteca importantissima. Lo sappiamo grazie ai suoi appunti, agli elenchi che abbiamo ritrovato sparsi tra i vari codici. Anche i suoi disegni degli animali sono il suo modo di capire il mondo, capire come si muovono, come sono fatti. Leonardo è un intreccio di scienza e arte: usa la scienza per esprimere meglio la sua arte, usa l’arte per capire la scienza.
Espressione dei suoi pensieri e dei suoi studi sono i suoi famosi codici: si tratta di disegni, schemi tecnici, annotazioni personali, battute di spirito, il tutto annotato con la sua scrittura speculare, orientata da destra a sinistra. Si tratta di migliaia di fogli di diverso formato e ne sono giunti fino a noi circa 8000, ovvero 1/3 di quanto ha realmente scritto. Leonardo avrebbe voluto riordinarli e classificarli, ma non riuscì mai. Alla sua morte li lasciò a Francesco Melzi, uno dei suoi allievi più cari, che li riportò a Milano nel 1523. Ma alla morte di Melzi, gli appunti furono in parte regalati, in parte venduti, in parte rubati.
A noi interessano dei particolari di questi codici: gli intrecci, i nodi vinciani! Sono intrecci che sembrano realizzati come scarabocchi per passare il tempo, gli stessi che tutti facciamo quando siamo annoiati, ma possono essere intrecci che costituiscono uno studio preparatorio per altre opere, oppure schemi per le sue famose macchine, oppure ancora decorazioni delle sue opere più famose (compare l’immagine della Dama con l’Ermellino, con l’ingrandimento di un particolare, un fregio del vestito che riporta, appunto, un intreccio). Tra le sue opere spiccano anche i labirinti, amati dai nobili, per i quali costituivano un passatempo.
Leonardo è vissuto a cavallo tra 1400 e 1500, mentre la nascita della topologia si attesta intorno al 1735, perciò lascerei la parola a Alunn09.
Alunn09: Grazie! Direi che è il momento di parlare della nascita della topologia, con l’opera di Eulero dedicata ai sette ponti di Konigsberg…
Al sentir nominare i ponti di Konigsberg, gli animatori di Grafo-mania presenti in sala salgono sul palco: Alunn10, Alunn11, Alunn03, Alunn12 e Alunn13
Alunn03: Se si parla di ponti di Konigsberg, le persone più adatte per parlarne siamo noi, visto che gestiamo il laboratorio di BergamoScienza dedicato a questa bellissima città. Dovete sapere che a Konigsberg ci sono sette ponti e, nella prima metà del 1700, gli abitanti, la domenica pomeriggio, amavano passeggiare su di essi, cercando un modo per passare su ogni ponte una volta sola, ma percorrendoli tutti. Per spiegarvi come fare, abbiamo deciso di rappresentare fisicamente la situazione. La città è divisa in quattro parti dal fiume Pregel e qui ci sono quattro animatori che possono rappresentarle e possiamo prendere questi nastri (sono stati predisposti dei nastri sul tavolo) per realizzare i ponti. Questi due (indicando Alunn12 e Alunn13) sono le due isole, mentre gli altri due sono le sponde del fiume. La prima isola è collegata ad ognuna delle sponde da due ponti (prende quattro nastri e li dispone in modo che colleghino l’isola alle rive), la seconda isola è collegata ad ogni sponda da un ponte (fa la stessa cosa con altri due nastri) e infine le due isole sono collegate tra loro da un ultimo ponte (ed ecco collocato l’ultimo nastro). Vediamo se c’è un volontario tra il pubblico per aiutarci con questa dimostrazione (sale sul palco Alunn14). Chiediamo a Alunn14 di attraversare tutti i ponti una sola volta: ogni volta che passerà sul ponte, lasceremo cadere il nastro corrispondente a mostrare che quel tratto di strada non si può ripercorrere.
Alunn14 fa un paio di tentativi, si chiama sul palco anche un altro elemento del pubblico (completamente ignaro) perché faccia il proprio tentativo, ma alla fine Alunn08 reagisce con impazienza:
Alunn08: Direi che il nostro pubblico ha capito benissimo come funziona. Se vogliono sapere qual è la soluzione, non hanno altra scelta che partecipare ai laboratori: a proposito, domenica pomeriggio avete l’ultima occasione per farlo. I laboratori si svolgono a scuola dalle 14.00 alle 17.30. Vi aspettiamo! (dopodiché fa cenno ad Alunn09 perché riprenda da dove è stato interrotto)
Alunn09: Grazie! Prima di essere interrotta, stavo dicendo che la nascita della topologia è evidenziata dall’opera di Eulero…
Prof4: (lanciandosi sul palco!) Ora, parlando di Eulero, non si può certamente tralasciare di citare la caratteristica di Eulero di uno spazio topologico! Ho giusto preparato delle slide per l’occasione... (la Prof5 lo interrompe subito)
Prof5: Sì, però cerchiamo di renderla un po’ più semplice di prima, che ne dici? Ti va di aiutarmi?
Prof4: Intendi con un esercizio pratico?
Prof5: Esattamente! Quando si parla di risultati matematici, spesso quelli più notevoli ci svelano regolarità inaspettate della realtà: uno di questi è indubbiamente la relazione di Eulero per i poliedri. Per farvi sperimentare quanto diciamo in maniera diretta, ora vi distribuiamo alcuni poliedri, che, come vedete, sono di vari tipi, e vi invitiamo, collaborando anche con i vicini, a fare questo semplice conteggio: contate il numero dei vertici del poliedro, sottraete il numero degli spigoli (lati), e sommate il numero delle facce... (alcuni alunni presenti prendono dei poliedri realizzati con il Polydron e li distribuiscono tra i presenti)
Pare proprio che si ottenga sempre 2.
Alunn05: (protestando vivacemente) Assolutamente no! Il mio ha dato come risultato zero!
Prof5: (lanciando uno sguardo di conferma a Prof4): Hai ragione! Ma tu non hai in mano un poliedro qualsiasi. Portalo qui! (Alunn05 sale sul palco, portando con sé un “poliedro toroidale”) Come vedete questo è diverso dai poliedri precedenti (nel frattempo mostra al pubblico in una mano il poliedro toroidale e nell’altra un cubo e un tetraedro). Perché è diverso dagli altri due?
Alunn05: (con entusiasmo) Perché è giallo!
Prof5: (infastidito): Direi che il colore non è così significativo. Qual è la differenza? Pensateci bene!
Alunn05: (dopo averci riflettuto un po’) Ha un buco!
Prof5: Proprio così: in effetti, si potrebbe dimostrare che il calcolo “vertici – spigoli + facce” della relazione di Eulero è influenzato dalla presenza di buchi. Sorprendente, no? Ora direi che possiamo lasciare di nuovo la parola a Alunn09 (invita Alunn09 a riprendere posto sul palco)
Alunn09: Grazie! (timidamente. E poi, rivolgendosi al pubblico) Eccoci ri-ritrovati! Direi che possiamo andare avanti con il nostro percorso, allora. L’ultima protagonista della nostra mostra è Maryam Mirzakhani. Nata a Teheran nel 1977, Maryam, fin da piccola, amava inventare storie e immaginava ragazzine che compivano grandi imprese. Leggeva parecchio, ma pare non amasse molto la matematica, e non mostrava di possedere un talento particolare. La sua insegnante di matematica del primo anno non vede in lei alcun talento e Maryam si convince di non essere molto brava. La prima persona che riesce a far nascere in Maryam l’interesse per la matematica è il fratello maggiore, che le racconta la storia di Friedrich Gauss e della formula per sommare i numeri naturali. Maryam comincia a intuire che la matematica potrebbe essere più interessante di quanto le era parsa fino a quel momento. A undici anni, conosce Roya Beheshti Zavareh, che ora è docente di matematica alla Washington University. Compagne di classe anche alle superiori, sentono parlare delle Olimpiadi internazionali di Informatica e decidono di partecipare, ma devono chiedere l'intervento della Preside del loro istituto, perché le competizioni sono chiuse alle donne. La prima partecipazione è nel 1994 a Hong Kong, dove Maryam vince la medaglia d’oro con un punteggio di 40 su 42, mentre nel 1995, in Canada, ottiene uno strabiliante punteggio pieno di 42 su 42. A quanto dice, la partecipazione alle Olimpiadi le ha mostrato la bellezza della matematica. Prova forti emozioni, e se in un primo momento la considerava una sfida, poi comincia a divertirsi e le piace l’opportunità che le viene data di pensare ai problemi di matematica. La bravura acquisita le apre le porte di Harvard, dove si ritrova Curtis McMullen come advisor, uno dei matematici più importanti del mondo. Conclude il dottorato nel 2004 e con la sua tesi dimostra una congettura aperta da anni. Nel 2008 si sposa con Jan Vondrak, e nel 2011 dà alla luce Anahita. Nel 2009 approda a Stanford e comincia la sua collaborazione con Alex Eskin, dell'Università di Chicago. La loro collaborazione li porta a raggiungere vette inesplorate, ma li obbliga anche a confrontarsi con le difficoltà: per due anni spendono lavoro e fatica e, nonostante la carenza di progressi, Maryam si mantiene positiva, grazie alla sua stabilità mentale e alla fiducia in sé stessa. Per raggiungere la cima, Maryam e Alex sono dovuti tornare al punto di partenza e, con pazienza, sperimentare un nuovo approccio per concludere il percorso. [7] Della matematica di Maryam, però, non sono in grado di parlare e ci dirà qualcosa la Prof2, alla quale cedo la parola prima che mi interrompa!
Prof2: Maryam è appassionata alla matematica delle superfici: qual è la distanza minore tra due punti? Sappiamo che nel piano è una linea retta. Su una sfera, è un arco della circonferenza massima. E su una ciambella? O su una ciambella con molti buchi? Nessuno conosceva le risposte. Se cammino in linea retta su una sfera, torno al punto di partenza. E anche su quello che i matematici chiamano un toro (e il resto del mondo chiama ciambella), se scelgo adeguatamente il mio percorso, posso tornare al punto di partenza. Ma potrei anche trovare un cammino infinito, che continua senza mai incontrare di nuovo sé stesso. Ce ne sono tanti che soddisfano questa caratteristica e sono tutti diversi tra loro: immaginiamo una formichina che si muove sulla superficie di questo salvag… ehm, toro! (presenta il percorso usando un salvagente e un nastro colorato, che viene avvolto attorno al toro) Potrebbe continuare all’infinito senza mai tornare al punto di partenza. Maryam non ha paura di mettersi alla prova per trovare una risposta e con Alex Eskin riesce a dimostrare il teorema noto come “Teorema della bacchetta magica”, perché risolve problemi che gli scienziati stavano affrontando da anni. Porta un cambiamento poderoso, nella matematica e non solo. Grazie ad esso, gli astronauti possono programmare percorsi più sicuri per le loro astronavi, i meteorologi possono predire il tempo più velocemente e con maggiore accuratezza, i ricercatori possono capire come si diffonde un’epidemia. Sono stati sufficientemente chiara Alunn09?
Alunn09: Sì, grazie! Maryam è stata la prima donna ad essere insignita della Medaglia Fields, nel 2014, e quando ha ricevuto la mail da parte della presidentessa dell’Unione Matematica, che la informava del conferimento del premio, Maryam, pensando si trattasse di uno scherzo, ha eliminato il messaggio.
Purtroppo, quando le è stato conferito il premio, Maryam era già sofferente per un cancro al seno ed è mancata nel 2017, a soli quarant’anni. La sua opera le è sopravvissuta ed è stato grande il segno che ha lasciato nella matematica.
Penso che sia ora di chiudere questo nostro percorso che è stato storico, artistico, matematico e costellato di leggende e teoremi strani. Forse siamo riusciti a convincervi che la topologia non è così male. Prof1, che dice? Le piace un po’ di più ora?
Prof1: Direi che mi avete convinta! Potrei persino pensare di realizzarci un’edizione di BergamoScienza!
Alunn07 (correndo verso il palco): c’è un’ultima cosa… [8]
Realizzato con il contributo di Carolina Bergamini, Chiara Bertoni, Luca Campagnoni, Asia Corna, Francesco Mognetti, e dei ragazzi che hanno partecipato ai laboratori di Topo-Scienza realizzati presso il nostro istituto, per partecipare al festival di BergamoScienza. L’articolo è la trascrizione (quasi) fedele della conferenza presentata al pubblico mercoledì 11 ottobre, nella Sala degli Affreschi dell’Accademia Tadini. Grazie al curatore dott. Marco Albertario per l’ospitalità e per le idee, sparse qua e là, grazie alle quali è stata realizzata la mostra presentata nel corso del Festival.
In allegato le slide realizzate per l'occasione
Bibliografia:
[1] La realizzazione di una bottiglia di Klein a partire da due nastri di Mobius, con il filmato di Numberphile, nel quale Cliff Stoll, appassionato di bottiglie di Klein, mostra come si può realizzare: https://arbitrarilyclose.com/2020/04/17/mathartchallenge-day-33-mobius-strip-klein-bottle/
[2] I pantaloni topologici: https://youtu.be/dGi1ibYQWFk?si=pW2gPNnU6uej3vDz
[3] Il teorema della palla pelosa spiegato da Raffaella Mulas con la sua matematica danzante: https://youtu.be/Eeki_8Hvm5E?si=mo4DJ1XFOMLqOPCw
[4] Ben Orlin, Math with bad drawings – Illuminating the ideas that shape our reality, Black Dog & Leventhal Publishers, New York
[5] dall’articolo di Oggiscienza del 28 gennaio 2019, “Sbrogliare il DNA con la teoria dei nodi” di Luisa Alessio https://oggiscienza.it/2019/01/28/teoria-dei-nodi-dna/index.html
[6] dal blog Matetango di Annalisa Santi, la spiegazione dei nodi borromei: http://annalisasanti.blogspot.com/2018/10/dallo-stemma-dei-borromeo-alla-teoria.html#:~:text=Il%20%22nodo%20borromeo%22%20si%20presta,come%20Corpo%2C%20Mente%20e%20Psiche.
[7] video sulla vita di Maryam Mirzakhani realizzato in occasione di #peopleformath2023 https://youtu.be/euZ_vbHMHK4?si=gFH_08MaMby6jgZt
[8] Johann Sebastian Bach, Canone 1 a 2 https://youtu.be/Y0_DeHSTLHU?si=0j0YM-v_Mg_Mr68n
“Il merlo, il merlo nella luce”
(poesia gaussiana)
Benvenuti all’edizione numero 171 del Carnevale della matematica, dal tema “matematica fantasiosa”! È la prima volta che ospito il Carnevale e, devo ammetterlo, sono un po’ emozionata!
Il 171 si fattorizza 3x3x19: Dioniso, come da tradizione, ha inviato la sua cellula melodica, caratterizzata da un salto di sesta minore, come se il merlo volesse farci riflettere sull’ossimorica qualità di una luce oscura.
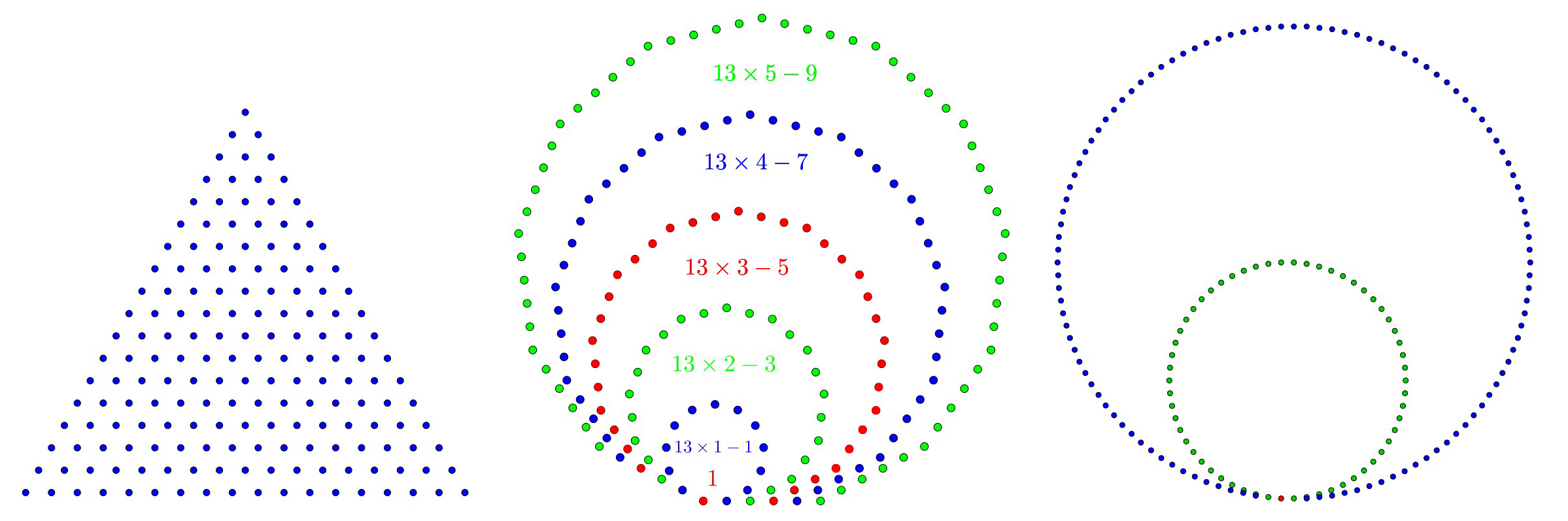
Oltre a essere un gioco di azione e avventura sviluppato da Betagames Group, 171 è un numero difettivo, visto che la somma dei suoi divisori è 89<171. Oltre a essere un numero palindromo nel sistema numerico decimale e nel sistema di numerazione posizionale a base 7 (333), è un numero di Harshad, cioè è divisibile per la somma delle sue cifre. È parte di ben 7 terne pitagoriche, ma sempre come cateto, ed è il diciottesimo numero triangolare, il sesto numero 13-gonale e il terzo numero 58-gonale:
171 è anche il trentaseiesimo numero fortunato, che si ottiene con un crivello simile a quello di Eratostene:
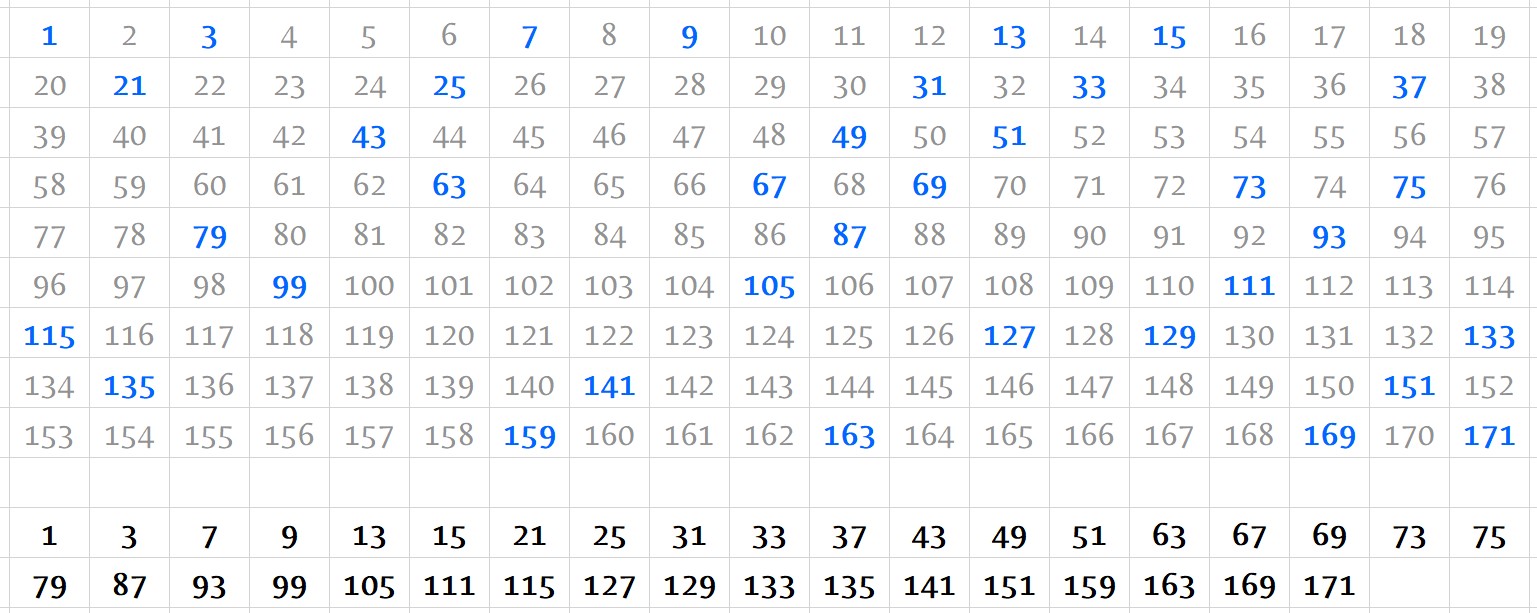
Si tiene l’1 e si tolgono tutti i secondi numeri, ovvero tutti i numeri pari. Il primo numero che si incontra a questo punto è il 3, perciò si contano due numeri e si esclude il terzo rimasto, il 5, e si procede così con 11, 17… fino a 167, nel caso della griglia che ho proposto. Oltre a 1 e 3, ora abbiamo il 7, perciò contiamo 7 numeri (sempre a partire dall’1) ed escludiamo il settimo, dal 19 fino al 165. Ora incontriamo il 9 e procediamo allo stesso modo cancellando 27, 57, 91, 121 e 153. Procedendo con la stessa regola fino a quando possibile, otteniamo la sequenza indicata.
Questi sono i contributi del carnevale:
Roberto Zanasi prosegue la rivisitazione della Divina Commedia in chiave scientifica con Inferno, Canto XIX, dove si parla di inversione di gravità e di Richard Gere poco vestito.
Dioniso continua ad esplorare il libro I paradossi di Zenone di Vincenzo Fano, che è stato uno dei punti di riferimento per il lavoro di ricerca per il suo libro, Il mistero della discesa infinita. In questa seconda parte, I contributi di Aristotele al paradosso della dicotomia, riporta una sintesi delle considerazioni di Fano relative alle interpretazioni aristoteliche del paradosso della dicotomia. In Guida veloce in città: vantaggi e svantaggi, Dioniso segnala una puntata di Radio3 Scienza, “Andavo a 30 all’ora…”, riassumendo i vantaggi e gli svantaggi in una tabellina, che potrebbe essere estremamente utile a scuola quando si parla di sicurezza stradale, applicazione della cinematica all’educazione civica.
Leonardo Petrillo propone un post dal suo blog Scienza e Musica, di carattere puramente divulgativo, adatto anche a un lettore abbastanza a digiuno di fisica e matematica, focalizzato nell’illustrare un importante modello classico della conduzione elettrica: il modello di Drude (introdotto nel 1900). Nella parte conclusiva dell’articolo, è presente un breve cenno inerente ad una rilevante verifica relativamente recente (2006) del suddetto modello, da parte di un duo di scienziati tedeschi.
Annalisa Santi ha rispolverato un post di qualche anno fa: dopo il 171 fortunato, sappiamo che in matematica si parla di Numeri Felici, Amici, Socievoli e di Numeri Fidanzati (e ci sono persino i “promessi sposi” 48 e 75), ma Ci sono i Numeri dell’Amore? Per trovare i Numeri dell’Amore è necessario uscire dalla visione matematica ed entrare in quella esoterica. E qui non si pretende certo di definire verità dimostrabili ma di sfruttare, secondo criteri assolutamente indimostrabili e soggettivi, la costanza dei numeri come dato rassicurante nel regno fluttuante dell’amore.
Piotr R. Silverbrahms, a nome dei Rudi Matematici, ha inondato la mia casella di posta elettronica di gentilezza e informazioni, spiegandomi come destreggiarmi in questo nuovo mondo. Il primo contributo è un PM, ovvero un “Paraphernalia Mathematica”, un articolo che tratta di argomenti generali – interessanti e curiosi – di matematica. È la rubrica storica della ben nota e-zine “Rudi Mathematici” (su questo sito, il loro logo è stato ospitato per 14 anni), ed è curata in persona dal fondatore, Rudy D’Alembert. Nel caso specifico, l’articolo fa parte di una piccola serie, chiamata “oltre Platone”, con evidente riferimento a superare i vincoli dei solidi platonici. È la seconda puntata della serie, e il titolo di questo episodio è Ricomincio da tre, un omaggio a Massimo Troisi e un riferimento al fatto che, pur essendo alla seconda puntata, si ricomincia a parlare di triangoli.
Il secondo contributo è un Q&D, ovvero un “Quick and dirty”, una sorta di problema dall’esposizione assai breve e dalla soluzione veloce, anche se il “dirty” specifica che magari, la soluzione, tanto veloce non è. Curve colorate parla di curve chiuse che si incrociano.
Da una rubrica all’altra, arriviamo a quello che, secondo i Rudi, è un “post istituzionale”. Oltre alla famosa e-zine, i Rudi Matematici curano una rubrica sul mensile “Le Scienze”, nella quale propongono un problema: il blog consente al gruppo di mantenere aperto il dialogo con i lettori, che hanno voglia di confrontarsi con il problema proposto e di suggerire le proprie soluzioni. L’ultimo numero di “Le Scienze”, quello di agosto, era il 660 e Il problema di agosto (660) – Mezzogiorno in comune, un problema di percorsi, anzi, di incroci.
Con poca fiducia di riuscire a rispettare i tempi (e chi segue la e-zine sa il perché), i Rudi Matematici disperavano di riuscire a pubblicare altro, ma alla fine è arrivato il 12 settembre 1900: Buon compleanno Haskell!. In questo compleanno, viene davvero celebrata la fantasia, visto che si parte dalle definizioni di Euclide e, percorrendo un sacco di antiche strade romane, si finisce nel bel mezzo della logica combinatoria.
Mauro Merlotti, autore del celebre Zibaldone Scientifico, propone due post: nel primo si parla di curve ad ampiezza costante, cioè di figure che, come il cerchio, hanno la stessa larghezza in tutte le direzioni. Abbiamo bisogno di un po’ di fantasia per capire che se le posizioniamo tra due rette parallele, possiamo farle ruotare mantenendo sempre le rette tangenti alla figura e alla stessa distanza tra loro! Il secondo è dedicato alla pizza al taglio e, dopo aver illustrato diversi modi (non convenzionali) di spartirsi una pizza, Mauro regala un po’ di pizza anche al teorema di Pitagora!
Maurizio Codogno conferma la sua fama di scrittore prolifico e ci regala una lunga serie di quizzini: quadrati alternati, molto semplice, e Vela, facile, ma funestato da una serie di errori; trapezio rettangolo, problemino geometrico facile e dall’1 al 5, una facile somma (se si sa come prenderlo); scegli la scatola è un po’ più complicato rispetto ai precedenti e ha a che fare con i codici a correzione di errore; numeri paladini ha una parte facile e una che richiede qualche conto in più, mentre numeri basici richiede un po’ di conti; il terzo maggior fattore è una semplice (?) applicazione di proprietà di fattorizzazione, primi somma e differenza di primi è molto facile; somme di numeri dispari non primi non è uno scioglilingua ma un quizzino abbastanza semplice, anche se richiede qualche conto, come pure insiemi sum-free; Doubleback Alley non è difficile, ma Maurizio ha trovato divertente ambientarlo; il sistema MIU arriva direttamente dal celebre Gödel, Escher, Bach.
Noto per le sue recensioni anche al di fuori del circuito matematico, durante l’estate Maurizio ha letto Il mistero della discesa infinita di Flavio Ubaldini, un bel romanzo “matematico” di cui si è parlato sopra; L’infinito, di Claudio Ternullo e Vincenzo Fano, che merita la fatica di affrontarne una lettura non semplice; Argomentare di Paolo Artuso, che contiene un utile ripasso della logica. Di Joseph Mazur, Maurizio ha letto Storia del tempo, ma ritiene che gli altri libri di questo autore siano migliori; con Algoritmi, monaci e mercanti di Giorgio Ausiello, si può scoprire come, nonostante tutto, nei mille anni del Medioevo anche in Europa si sia fatta matematica: poca, utilitarista, ma comunque matematica. La traduzione inglese di Arithmetical, Geometrical and Combinatorial Puzzles from Japan di Tadao Kitazawa non è il massimo, ma è interessante vedere giochi per nulla simili ai nostri soliti; Trigonometry – A very short introduction di Glen van Brummelen permette di indagare la trigonometria vista dal contesto della matematica e infine The Britannica Guide to Algebra and Trigonometry, edito da William L. Hosch, è sconsigliato, a meno di non avere curiosità storica su come questi due campi della matematica siano nati e cresciuti.
Per la serie povera matematica, troviamo Mai fidarsi dei fisici che scrivono di matematica, sulle affermazioni un po’ peculiari di Michio Kaku sulle geometrie non euclidee; Come non usare gli Invalsi ci mette in guardia: gli Invalsi mostrano differenze tra varie categorie di studenti, ma se non si specifica come sono misurati i dati, si parla sul nulla. Parlare di Invalsi porta necessariamente a domandarsi: Invalsi: Chi è che non sa leggere e far di conto? E la risposta di Maurizio è la stessa di molti di noi: i giornalisti… Scuole aperte (ma volontariamente) offre un punto di vista diverso sulle vacanze scolastiche estive, visto che segnalare il numero di settimane di sospensione delle lezioni non è statisticamente corretto. Con il post Il senatore Borghi (Aquilini) e il riscaldamento che non ci sarebbe, Maurizio commenta che il senatore Borghi scrive bene e così nasconde le proprie fallacie a proposito del riscaldamento climatico. Il 250% in meno ha attirato l’attenzione di Lucio Malan, che sa fare i conti, ma confonde l’ignoranza con la faziosità, mentre Com’è difficile spiegare ci racconta come a volte la matematica possa fare comodo per confondere un po’ le acque e arrampicarsi sugli specchi.
Per la serie matematica light, Ci sono solo sette numeri la cui radice cubica è uguale alla somma delle loro cifre è una curiosità senza reale importanza; Dati veri ma presentati male riporta la spiegazione di Giulio Betti in merito al grafico sul calo del ghiaccio artico, che è corretto ma fuorviante; Perché non fidarsi delle AI generative, parte N, ci ricorda che a una AI possiamo chiedere tante cose, ma se proviamo a farle fare un po’ di matematica sbaglia peggio di uno studente incapace.
I contributi di Maddmaths! sono come sempre numerosi e variegati:
Sulla cresta dell’onda: intervista con Roberta Bianchini, vincitrice del Premio SIMAI 2023
Roberta Bianchini è ricercatrice all’Istituto per Applicazioni del Calcolo “Mauro Picone” IAC-CNR di Roma. Nel corso del Convegno Biennale SIMAI 2023, svoltosi a Matera, ha ricevuto il Premio Biennale SIMAI 2023 “Fausto Saleri”, per la sua attività di ricerca nella matematica applicata. Il premio è rivolto a ricercatori e ricercatrici under-35. Dopo la premiazione, l’ha intervistata Marco Menale.
Conferenza pubblica di Eduardo Sáenz de Cabezón – Il video integrale
Durante il XXII Congresso UMI che si è tenuto a Pisa dal 4 al 9 settembre scorso, il famoso divulgatore matematico Eduardo Sáenz de Cabezón ha tenuto una conferenza (in inglese) dal titolo molto interessante: How to speak about mathematics to a broad audience, ora disponibile su YouTube.
Archimede 2/2023: speciale valutazione
È uscito il numero 2/2023 della rivista Archimede che è un numero speciale dedicato alla Valutazione. Vi proponiamo il sommario del direttore Roberto Natalini: “Nella continua riflessione sull’insegnamento e sull’organizzazione scolastica, un ruolo spesso trascurato è quello della valutazione. Eppure, senza valutazione è difficile capire se l’azione didattica sia stata efficace, come sia possibile migliorarla e soprattutto non renderla sempre più personalizzata. Per queste ragioni questo numero di Archimede è dedicato proprio alla valutazione, con tre contributi autorevoli e abbastanza complementari tra di loro, per ribadire la complessità della tematica. Apriamo con un articolo di Ketty Savioli, che ci presenta la valutazione “per” l’apprendimento nella scuola primaria (l’articolo è liberamente scaricabile sul sito Mondadori). Segue un articolo molto ben documentato di Rossella Garuti e Nicoletta Nolli su come funzionano e l’impatto che hanno avuto le prove INVALSI somministrate con il computer (Computer based test, CBT). Completa questa rassegna una riflessione di Roberto Ricci, presidente dell’INVALSI, sull’analisi degli apprendimenti in matematica che emerge dalle prove standardizzate. La splendida copertina e il fumetto sono dedicati alla figlia di Vito Volterra, Luisa, e aprono una breve trilogia di Alessandro Bilotta e Dario Grillotti sul matematico fondatore del Cnr che ci accompagnerà per tutto il 2023, un’appedice indispensabile alla loro graphic novel La funzione del mondo – Una storia di Vito Volterra.”
Recenti progressi su un altro problema di Erdős
I problemi posti da Erdős non finiscono mai. Recentemente c’è stato un notevole progresso su un una sua vecchia congettura sulla “densità” degli insiemi di numeri interi. Per saperne di più e capire meglio di cosa si tratta lasciamo la parola al nostro Alessandro Zaccagnini.
Riuscirà la matematica a battere il gerrymandering?
Continuiamo a parlare di gerrymandering, ovvero la pratica fraudolenta che consiste nel formare distretti elettorali in maniera partigiana, in compagnia di Nicola Apollonio.
Un incontro con László Lovász
László Lovász è un matematico ungherese e un Professore Emerito all’Università Eötvös Loránd di Budapest. È stato Presidente dell’Unione Matematica Internazionale ed è stato Presidente dell’Accademia delle Scienze Ungherese. È stato anche uno dei principali collaboratori di Paul Erdős. Raffaella Mulas lo ha intervistato nel giugno 2023, durante una visita all’Alfréd Rényi Institute of Mathematics a Budapest.
Materiali didattici sui mercati finanziari
Pubblichiamo del materiale didattico proposto in un sito web dalla Prof.ssa Rosaria Trisolino, sull’educazione finanziaria che speriamo possa essere utile al lavoro di classe nelle scuole superiori. Precede il riferimento al sito una breve introduzione della docente.
Matematica a fumetti: un nuovo librino di MaddMaths!
Negli ultimi anni sono stati pubblicati tanti fumetti a tema matematica. Con questo nuovo librino di MaddMaths! vi proponiamo una schedatura abbastanza completa di alcune opere recenti appartenenti a questa categoria. L’autrice è Gulsin Celik, studentessa dell’Università di Perugia.
Tre proposte per l’insegnamento della matematica nella scuola
Riprendiamo la discussione sul cambiamento dell’insegnamento della matematica nella scuola proponendovi alcune riflessioni e tre proposte di Giovanni Righini, professore ordinario di Ricerca Operativa presso l’Università degli Studi di Milano, da sempre attivo anche nell’ambito della didattica della matematica.
Eventi:
A Camerino torna Comunicamat – Comunicare la Matematica 2023
Comunicamat 5 – la quinta edizione del congresso “Comunicare la matematica” – ritorna con la stessa formula degli ultimi anni da mercoledì 4 a venerdì 6 ottobre 2023: 3 pomeriggi a distanza, dedicati a interventi sulla comunicazione e la divulgazione della matematica.
Incontri con la matematica n. 37 – dal 10 al 12 novembre 2023 a Castel San Pietro
Ritorna Incontri con la Matematica n.37, il tradizionale Convegno di Castel San Pietro Terme per insegnanti di Matematica, che quest’anno si svolgerà in presenza da venerdì 10 a domenica 12 novembre 2023.
Letture matematiche
“oltre Marie”: come superare gli stereotipi di genere nella scienza
Il 6 settembre esce in libreria e online “Oltre Marie”, un libro di Nastassja Cipriani e Edwige Pezzulli dedicato alle prospettive di genere in ambito scientifico. Ce ne parla Chiara de Fabritiis (Coordinatrice del Comitato Pari Opportunità dell’UMI).
Rivoluzioni matematiche: il Teorema di Eulero sui grafi
Con il numero di settembre de Le Scienze troverete in allegato il dodicesimo dei venti volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al Teorema di Eulero sui grafi ed è a cura di Alberto Saracco.
Rivoluzioni matematiche: il Teorema dei quattro colori
Con il numero di agosto de Le Scienze troverete in allegato l’undicesimo dei venti volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al Teorema dei quattro colori ed è a cura di Donatella Iacono e Sabina Milella.
Storia sconosciuta di Évariste Galois, Fabrizio Luccio e Linda Pagli
Brevi consigli per letture matematiche. “Storia sconosciuta di Évariste Galois – matematico e rivoluzionario” di Fabrizio Luccio e Linda Pagli.
L’arte della statistica, David Spiegelhalter
Brevi consigli per letture matematiche. “L’arte della statistica – Cosa ci insegnano i dati” di David Spiegelhalter, consigliato da Marco Menale.
Letture estive consigliate dalla redazione di MaddMaths!
L’estate è spesso tempo di letture ed è sempre comodo avere una lista di libri tra cui poter scegliere. Ovviamente, dati i nostri interessi, queste letture avranno uno sfondo o una motivazione matematica, a volte non troppo stretta, ma sempre presente. Altri consigli li trovate nella nostra rubrica Letture matematiche, che potete trovare a questo link. E poi non smettete dopo l’estate!
La lente matematica di Marco Menale
I criteri di Bradford Hill
I criteri di Bradoford Hill sono utilizzati negli studi statistici randomizzati per riconoscere rapporti di causalità tra grandezze. Perché correlazione non è causalità.
I modelli multiscala
Possiamo descrivere l’evoluzione di un fenomeno a più livelli. Come una lente, ci avviciniamo e ci allontaniamo per vedere dettagli e particolari. È l’approccio dei modelli multiscala. Ce ne parla Marco Menale.
Dinamica delle opinioni: i modelli cinetici
La matematica aiuta a comprendere la dinamica delle opinioni. Dalla loro diffusione, fino a persuasione e polarizzazione. Diversi modelli cinetici sono stati sviluppati negli ultimi anni. Ce ne parla Marco Menale.
È ora di dare il mio piccolo contributo a questa ricca selezione di matematica.
Ho scelto la matematica fantasiosa, perché è la matematica con la quale mi sono confrontata nel corso dell’estate. Dal 2016, l’estate è il momento per me, e per altri insegnanti della mia scuola, per dedicarsi alla progettazione dei laboratori che verranno proposti nel corso dell’imminente edizione del Festival di BergamoScienza (siamo alla sua XXI edizione e si svolgerà nella prima metà di ottobre). Il Festival ha una particolarità che lo rende unico: oltre ad offrire conferenze e incontri con famosi premi Nobel, invita le scuole a mettere a disposizione i propri alunni perché diventino divulgatori scientifici e si facciano carico di far conoscere la scienza ai bambini delle scuole degli ordini inferiori (e, a volte, ai loro coetanei). Da laureati in matematica, abbiamo sempre scelto questa come oggetto dei nostri laboratori, e direi che, negli anni, la nostra scelta si è rivelata vincente! Quest’anno abbiamo scelto la topologia e, nel corso dell’estate, mi sono dedicata… all’uncinetto! Ho realizzato nastri di Mobius e bottiglie di Klein all’uncinetto seguendo due diversi metodi, ho realizzato tori in stoffa e all’uncinetto e, infine, ho cucito dei simpatici pantaloni, seguendo il suggerimento del filmato Topology riddles, al quale sono approdata mentre cercavo materiali sull’argomento. Nel filmato (davvero bello!) si parla di questi pantaloni realizzati da due matematiche della Cornell University, Tara Holm e Lila Greco, e ho deciso di realizzarli. Sui miei pantaloni ho pubblicato anch’io due video: uno short, in cui presento il funzionamento dei pantaloni, e un video più lungo nel quale descrivo (abbastanza nel dettaglio) la realizzazione dei pantaloni, perché qualcun altro possa provare a farlo. La cosa più interessante dell’intero procedimento, a parte i miei errori da sarta dilettante, è che spendere tempo per realizzare queste creazioni mi ha permesso di riflettere sulle proprietà topologiche di questi oggetti, a un livello di consapevolezza che non sarebbe stato possibile in nessun altro modo.
Un ultimo spunto, invece, non ha nulla a che fare con la topologia, ma con i numeri figurati con i quali si è aperto questo Carnevale: in realtà, la riflessione è avvenuta in estate, è nata da un dolce che mi piace preparare, ha coinvolto mio papà, e, come sempre quando si parla con lui, i tubi!
Questo è quanto…
Direi che la rassegna offre matematica per tutti i gusti. Ci si ritrova a ottobre!
La scelta della topologia per la nostra ottava partecipazione al Festival di BergamoScienza mi ha obbligata a fare i conti con questa parte della matematica che non ho mai amato particolarmente.
Eppure... un certo fascino l'aveva! Il nastro di Mobius, ad esempio, mi ha sempre affascinata: prendete una striscia di carta lunga circa 20 cm, alta 3 cm e incollatene gli estremi dopo aver fatto fare una torsione di 180° a un capo. Le caratteristiche di questo nuovo anello sono davvero particolari: se aveste incollato i due estremi della striscia senza aver realizzato la torsione, ne sarebbe uscito un piccolo cilindro, con due bordi e due superfici, quella interna e quella esterna. Il nastro di Mobius, invece, ha un solo bordo e una sola superficie, caratteristica che si può verificare empiricamente, usando una penna e, appoggiata la punta della penna in un punto dell'anello, si scopre che lo si può percorrere in tutta la sua lunghezza, tornando al punto di partenza.


C'è un altro modo per verificare che il bordo è unico: realizzare un nastro di Mobius all'uncinetto con il metodo indicato da Kathy Ceceri, che dà suggerimenti per realizzare un braccialetto. Quello delle foto è qualcosa di più di un braccialetto, visto che ha una massa di 1 kg, essendo realizzato con del filato molto grosso.
Lavorare all'uncinetto per realizzare oggetti topologici mi ha permesso di capire meglio queste superfici così particolari, a partire dal semplice toro (quello che i matematici chiamano toro, ma che il resto del mondo chiama ciambella!). Ho realizzato due diversi tori, uno all'uncinetto e uno, gigante, di stoffa. Sono completamente diversi, e non solo per la tecnica utilizzata: quello a uncinetto ha davvero la forma di una ciambella, con il punto basso che contrasta il punto alto esterno e crea quindi l'arrotondamento, mentre quella di stoffa è stata realizzata con un rettangolo di stoffa, ovvero matematicamente. In questo caso, la struttura non è rigidamente circolare, ma la forma varia a seconda di come viene preso il cuscino.


Ho realizzato, infine, alcune bottiglie di Klein, sempre all'uncinetto, completamente diverse tra loro. Dapprima mi sono imbattuta nel blog Arachne's Loom e grazie allo schema di Ruth, sono riuscita a realizzare un paio di bottiglie davvero simpatiche, che ho provveduto a imbottire di ovatta.
Le altre bottiglie di Klein sono state realizzate in modo diverso: ho unito due nastri di Mobius lungo il loro unico bordo per ottenere una superficie senza bordi, ma ho commesso un errore durante l'operazione. Pur consapevole che i due nastri dovevano avere chiralità opposta, non mi sono resa conto di averli realizzati con la stessa chiralità e ho dovuto scucire una parte del lavoro fatto. Poco importa... ho potuto concludere il percorso con una riflessione didattica, seguendo le fasi che avevano accompagnato la mia presa di consapevolezza.


Lo spunto per la realizzazione è nato da questa MathArt Challenge e da un video di Numberphile.
A mia mamma piacciono tantissimo le rose di pesche: un po’ di pasta sfoglia (si compra in rotolo, già pronta!), qualche pesca, un paio di cucchiai di marmellata di albicocche e via in forno!
Per il suo compleanno, non potevano mancare…

Ne avevo fatte in quantità e ne sono avanzate 7. Le ho disposte su un piatto, nel modo più “economico” (in termini di spazio) possibile. È la pratica a indicare la strada, ma anche la matematica ci dà una mano:
«Chiunque deve disporre lattine di fagioli in un ampio spazio, può contare su un teorema matematico, noto come Teorema di Thue, secondo il quale la disposizione esagonale permette di raggiungere la massima densità possibile. Pertanto, ancora una volta, come spesso accade con i quesiti matematici, la soluzione migliore risulta essere fondata su una delle strutture più semplici e meglio conosciute.» (R. Eastaway, J. Wyndham, Matematica dietro le quinte, edizioni Dedalo).
Le mie non erano lattine, ma piccoli muffin di pesche, dalla forma tondeggiante, come quelle delle lattine!
Mio papà vede le rose sul piatto. Dice che gli ricordano la Tenaris… strano! Mio papà ha passato quasi tutta la sua carriera lavorativa alla Tenaris e qualsiasi cosa gliela ricorda. Ma questa volta ha ragione: la Tenaris produce tubi e, quando vengono stoccati, sono disposti in modo da occupare il minor spazio possibile, quindi seguendo una struttura esagonale (come quella delle lattine di fagioli!).
«Se il fascio di tubi era più grande, mi pare diventassero 19.»
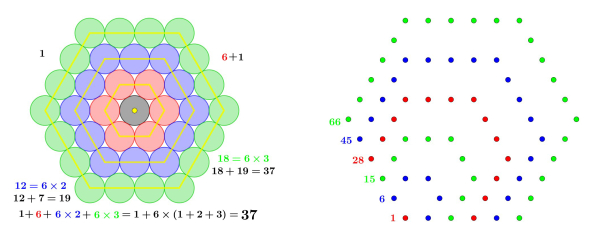
Il successivo numero esagonale è 19, ma sono numeri esagonali particolari, detti centrati. Così la disposizione dà la sequenza: 1, 7, 19, 37, 61, …
La si può costruire in questo modo: il primo numero è 1, poi si aggiunge 6, ovvero 6x1. L’esagono successivo ha i lati con 3 punti ciascuno, i vertici più il punto medio, perciò possiamo dire che l’esagono successivo avrà perimetro 12, in altre parole 6x2. Quello dopo ancora avrà 18 punti, cioè 6x3… e via così. Quindi, all’ennesimo esagono, avremo: 1+6(1+2+…+n-1), se consideriamo come primo esagono quello degenere e ridotto a un punto solo.
Erroneamente, avevo pensato ai numeri esagonali, ma i veri numeri esagonali sono quelli rappresentati nella figura a destra e la sequenza è diversa: 1, 6, 15, 28, 45, 66, …. Come si può notare, crescono più lentamente e danno luogo a un disegno diverso. Non solo: hanno una formula diversa! Io me la sono costruita e se vogliamo arrivare a 66, otteniamo:
1+(6x1-1)+(6x2-3)+(6x3-5)+(6x4-7)+(6x5-9)=1+6(1+2+3+4+5)-(1+3+5+7+9)=66