Visualizza articoli per tag: didattica
È la fisica, bellezza!
Pubblicato a maggio di quest’anno, «È la fisica, bellezza!», edito da Edizioni Dedalo nella collana scienzaFACILE, è l’ultima fatica di Federico Benuzzi. Docente di matematica e fisica in un liceo di Bologna, giocoliere che con i suoi spettacoli diverte e fa pensare, Benuzzi è un divulgatore a tempo pieno. Questo libro è frutto di un lavoro cominciato molto prima della pubblicazione, con una serie di video – richiamati poi nel corso della narrazione – condivisi sui social: è facile immaginarlo mentre cammina in montagna da solo, costruisce un discorso nella sua testa e poi accende la fotocamera, senza nulla lasciare all’improvvisazione.
La consapevolezza dichiarata in apertura che «la fisica è un punto di vista privilegiato per osservare il mondo» è diventata la sfida di Federico per sé stesso: quella di essere divertente e narrativo, ma al tempo stesso rigoroso, quella di avere uno stile divulgativo nel raccontarci quello che per lui è «mestiere, senso, vita». Nella doppia copertina che caratterizza gli ultimi libri pubblicati in questa nuova collana della Dedalo, sono riportati i temi principali: Didattica, Cambiamenti climatici, Supereroi. Il fulcro centrale, attorno al quale si sviluppa il discorso, è la didattica, anche se la narrazione ha come obiettivo la trattazione dei cambiamenti climatici, che non è solo la conclusione del percorso, ma il tema che permea il libro. In tutto questo, i supereroi planano con leggerezza a metà percorso.
Il libro è diviso in cinque sezioni: la prima tratta della fisica quotidiana, e l’inizio, in leggerezza, mostra una normale mattinata al risveglio, quando ci confrontiamo con il mondo, applicando inconsapevolmente concetti fisici. Il primo Federico Benuzzi che incontriamo, quindi, è il docente, che spiega le parti principali della meccanica: si comincia con le leve, si procede con l’equilibrio, si passa alla caduta dei gravi e infine ci si concentra sul calore e sul galleggiamento, cominciando la marcia di avvicinamento ai cambiamenti climatici.
La seconda sezione è dedicata alla fisica dei giochi, non solo perché la fisica tira fuori il bambino che è in noi, ma anche perché fin da piccoli impariamo attraverso il gioco. Così troviamo il principio di conservazione dell’energia spiegato con un picchio ballerino con una piuma in testa, il secondo principio della termodinamica viene introdotto con un papero bevitore che fa impazzire Homer Simpson, il ping phon ci permette di indagare la legge di Bernoulli e di capire come un aereo possa volare, il radiometro di Crookes ci fa parlare della termodinamica ancora una volta, mentre la giostra diventa una metafora della rotazione terrestre.
La terza sezione è la fisica dei fisici, ovvero la fisica seria e difficile che si studia all’università e qui ho toccato con mano lo splendido equilibrio realizzato da Benuzzi con questo libro: se da un lato il peso della mia ignoranza mi trascinava verso il basso, impedendomi di interpretare correttamente la quotidianità con gli occhi del fisico (mi sono laureata in matematica), la spinta archimedea data dal fascino delle grandi vette, mostrate con sapienza in questa sezione, mi ha permesso di elevarmi un po’. Benuzzi guida sapientemente il lettore attraverso i meandri della relatività, con il paradosso dei gemelli e il GPS, racconta la fissione e la fusione nucleare, esplora la meccanica quantistica e parla di indeterminazione, torna di nuovo sulla relatività con quella generale e conclude con l’entanglement. Il tutto condito con metafore illuminate e illuminanti che ci permettono di cogliere l’essenza di una fisica così difficile, pur non potendo raccontare la verità dell’oggetto senza evitare forzature, «a riprova che la divulgazione non è sufficiente per capire una disciplina».
La quarta sezione è la fisica del fantastico che, come un cavallo di Troia, permette di conquistare il lettore con il fascino dei supereroi e della fantascienza: troviamo l’energia con Superman, la conservazione della quantità di moto con l’Uomo Ragno, l’attrito con Flash, i buchi neri nella fantascienza e la conclusione con un pot-pourri di errori distribuiti nei vari film.
L’ultima sezione è la fisica del clima: nella breve introduzione, Federico Benuzzi si assicura che sia chiara la distinzione tra meteo e clima, ci mette in guardia dai bias cognitivi che in qualche modo possono alterare la nostra percezione della realtà e ci parla dei modelli matematici. A differenza delle sezioni precedenti, nelle quali ogni singolo capitolo si concludeva con la proposta di una domanda al lettore e la risposta offerta tramite un video, in questo caso la domanda fa da apertura al capitolo successivo, in un crescendo che si conclude con un invito a non inventare scuse e a cercare un modo per attivarsi. Così come David Quammen, citato proprio in chiusura, con il libro Spillover diventa la cassandra della pandemia di Covid-19, anche Benuzzi, considerate le ultime alluvioni nei pressi di Bologna, può essere considerato un profeta. In realtà, tutto nasce dall’osservatorio privilegiato della fisica: se si riesce ad evitare di nascondersi dietro i bias cognitivi, non si può che diventare dei facili profeti di sventura.
La condivisione di consapevolezza che Federico Benuzzi fa con questo libro illumina il nostro percorso, realizzando gli obiettivi che si era posto nell’introduzione. Il libro è rigoroso, ma si mantiene leggero grazie al senso dell’umorismo dell’autore, è divulgativo, ma può rivelare la sua utilità anche in ambito didattico. Se già si conosce Federico Benuzzi, non si può che sentire la sua voce che ci racconta la fisica: questa impressione è enfatizzata dal doppio linguaggio del libro, grazie alla presenza dei QR code ai quali i tipi di Dedalo ci hanno ormai abituato, con riferimenti esterni che aiutano ad approfondire, con sottolineature che non appesantiscono la narrazione. Questo testo aiuta ad apprezzare la fisica, a capirla meglio, e a coglierla nel mondo attorno a noi, allenandoci all’utilizzo del metodo scientifico, abituandoci a porci delle domande e a cercare sapientemente delle risposte.
L'esame che... sorprende
La quarta (e ultima, per la commissione di cui ho fatto parte) giornata di prove orali è stata in qualche modo caratterizzata dalla scoperta dell’arte, perché, considerata la mia abissale ignoranza in materia, non potevo che restare sorpresa dal coinvolgimento della matematica.
Il primo documento era un’immagine che contrapponeva comunismo e capitalismo: ho trovato un articolo di Pietro Greco, pubblicato per Il Bo live a maggio 2018, intitolato Marx, il matematico che non ti aspetti. Anche se poi, nel corso dell’articolo, leggiamo che Marx non può essere definito un matematico di «primaria grandezza», di fatto è stato l’autore dei Manoscritti matematici, pubblicati solo recentemente, ai quali ha lavorato per tutta la vita. Con questo testo si mostra «capace di penetrare i fondamenti della scienza dei numeri» e ha due obiettivi: il primo era di «fondare l’economia su solide basi matematiche», mentre il secondo era di «fondare il calcolo differenziale su solide basi concettuali», mostrando così di non voler relegare la matematica al ruolo di ancella dell’economia, ma di riconoscerne «il valore culturale in sé».
Il secondo e il quarto documento hanno avuto a che fare, entrambi, con l’arte. Il secondo documento era uno dei quadri di De Chirico della serie Piazze d’Italia, nello specifico era il quadro Presente e passato. Il primo link che ho visitato parlava, in realtà, di Paolo Uccello che nel Quattrocento rappresentava atmosfere surreali, attraverso una distorsione della prospettiva. De Chirico ha trovato, in Paolo Uccello, una fonte di ispirazione: come esponente della Pittura metafisica, visto che «aspira a superare i limiti del visibile e del reale», attraverso uno spazio ordinato, con scene nitidissime, fatte da oggetti e forme riconoscibili e collocati in uno spazio «delimitato dalle forme geometriche». È stato solo in un secondo momento che ho trovato l’opera Nostalgia dell’infinito, datata 1913, «caratterizzata da una forte enfasi dell’aspetto geometrico che mette in evidenza angoli e spigoli presenti, i quali arrivano a trasmettere all’osservatore, intento nella ricerca di un’interpretazione personale dell’opera stessa, un senso di distacco». Infatti, essendo l’infinito «non descrivibile tramite forme e linee, che lo ingabbierebbero inevitabilmente», con questa rappresentazione De Chirico regala una sensazione di amarezza e rammarico: la nostalgia, appunto! E qui, il collegamento è davvero semplice, visto che l’analisi, oggetto di studio del quinto anno, è pervasa dall’infinito.
Il quarto documento è stato Il volto della guerra di Salvador Dalì e ho trovato un articolo davvero interessante di Silvia Benvenuti, pubblicato su MaddMaths!, Genio e sregolatezza: le passioni matematiche di Salvador Dalì. L’autrice esordisce dicendo «di voler sostenere che la matematica può essere, oltre che un valido supporto tecnico per gli artisti, anche un eccezionale stimolo creativo». La citazione di Dalì, riportata subito dopo, pare sostenere proprio questa tesi: «Devi, soprattutto da giovane, usare la geometria come guida alla simmetria nella composizione delle tue opere. So che i pittori più o meno romantici sostengono che queste impalcature matematiche uccidono l’ispirazione dell’artista, dandogli troppo su cui pensare e riflettere. Non esitare un attimo a rispondere loro prontamente che, al contrario, è proprio per non aver da pensare e riflettere su certe cose, che tu le usi.» I bozzetti preparatori mostrano proprio l’importanza di fissare alcune proporzioni, ma visto che si tratta di un grande artista, Dalì non si limita alla sezione aurea, dominio di tutti, va ben oltre. Troviamo, quindi, la topologia nella Persistenza della memoria, la quarta dimensione in Corpus Hypercubicus, e poi la teoria delle catastrofi. Dalì «è stato profondamente affascinato dalla matematica durante tutta la sua vita, e le sue opere riflettono in modo molto profondo questa passione», che, grazie ai suoi studi e alle amicizie matematiche, conosceva bene.
Chiudo questa rassegna di diciotto collegamenti un po’ fuori dagli schemi con una citazione di Albert Camus, tratta da Il mito di Sisifo: «L’absurde dépend autant de l’homme que du monde. Il est pour le moment leur seul lien» (traduzione di Google: L’assurdo dipende tanto dall’uomo quanto dal mondo. Per il momento è il loro unico legame). Per cercare di farmi un’idea, ho setacciato il web (come al solito): «In questa opera Camus negando qualsivoglia valore a un significato trascendente alla vita e al mondo, riconosce come assurda l’esistenza: senza un significato l’esistenza è irrazionale ed estranea a noi stessi. Resta dunque il suicidio», che però non risolve il problema, e non resta altra soluzione se non la “sopportazione”. In un primo momento, ho pensato alla dimostrazione per assurdo, ma mi è parso il collegamento citato all’inizio di questo percorso della resistenza partigiana con la resistenza elettrica, perciò ho cercato di andare oltre. L’idea del suicidio mi ha portato alla vicenda di Alan Turing, del quale, proprio pochi giorni fa, è stato celebrato il settantesimo anniversario della morte. Per celebrare l’avvenimento, Il Post ha proposto un articolo sul grande genio, protagonista della decodifica dei messaggi di Enigma durante la Seconda guerra mondiale, ma anche autore di un importante articolo del 1950, nel quale si pone un’importante questione: «Le macchine possono pensare?». Il test che porta il suo nome è diventato un punto di riferimento per chi si occupa di intelligenza artificiale ed è un problema quanto mai attuale, soprattutto per noi insegnanti che siamo chiamati a distinguere l’operato dei nostri alunni dall’opera di ChatGPT. Se non abbiamo grandi speranze in tal senso, stando a un articolo di Nature del luglio scorso, non ci resta altro da fare che investire le nostre energie su altro: ad esempio, a far nascere una passione…
Terza giornata di prove orali: L'esame che amerei
L'esame che amerei
La giornata di oggi è stata dominata dai grafici e, devo riconoscerlo, sono uno strumento effettivamente semplice ed evitano ai candidati collegamenti fantasiosi che suonano un po’ come un’arrampicata libera sugli specchi. Il primo grafico è collegato alla celebre frase di Nietzsche “Dio è morto” e rappresenta la distribuzione delle religioni nel mondo. Personalmente, mi sarebbe piaciuto sentir parlare della dimostrazione dell’esistenza di Dio di Gödel, o forse si sarebbe potuta aprire una riflessione, visto l’impazzare di ChatGPT, a partire dall’articolo, ormai datato, di MaddMaths! E questa prova ontologica dell’esistenza di dio? nel quale si racconta che Christoph Benzmüller dell’Università di Berlino e Bruno Woltzenlogel Paleo dell’Università di Vienna hanno verificato, con theorem provers, la prova ontologica, che di fatto è un esercizio di logica modale. Questa verifica «offre un ulteriore spunto al tentativo di formalizzare mediante linguaggi meccanici i metodi e le strategie del ragionamento matematico».
Anche il secondo argomento proposto aveva a che fare con dei grafici: in questo caso, si trattava della concentrazione della ricchezza in Italia e nel mondo, e i due grafici accompagnavano un piccolo estratto de I malavoglia di Giovanni Verga. Il grafico è stato riportato, nel dicembre 2017, sul quotidiano Avvenire: si riferisce al periodo 1995/2013 ed evidenzia l’aumento delle diseguaglianze sociali, secondo la ricerca di Salvatore Morelli, dell’Unità di studi sulle diseguaglianze dell’Università di New York, Paolo Acciari del ministero dell’economia, e Facundo Alvaredo, della Paris School of Economics.
Il terzo documento ha aperto una strada più interessante: si parla di Futurismo e l’opera presentata è Il dinamismo dell’automobile di Luigi Russolo, mentre l’articolo è stato pubblicato su MaddMaths! e porta la firma di Roberto Natalini. Nel 1940 Marinetti ha scritto il Manifesto della “Matematica futurista”, con la collaborazione del matematico Marcello Puma, e ha acquisito «la sintesi delle nuove matematiche discusse nei primi venticinque anni del Novecento, rivalutando i principi della probabilità, della casualità, del caos e la teoria dei giochi». All’inizio del XX secolo, la comparsa della tecnologia ha generato un cambiamento nell’arte, il Futurismo, ma ha generato un cambiamento anche nella matematica, che diventa «una matematica di guerra», mostrandosi come una «forza terribile» che «può dare un aiuto incomparabile». Siamo alla fine degli anni Venti e nasce l’Istituto per le Applicazione del Calcolo: il lavoro di Mauro Picone, del quale l’istituto porta il nome, permette il passaggio da un universo matematico a priori (quello ipotizzato da Galileo Galilei) a un universo da matematizzare attraverso i modelli.
L’ultimo documento della mattinata è stato scelto per lingua e letteratura spagnola: si parla della dittatura franchista e non può mancare il riferimento al libro di Chiara Valerio La matematica è politica, presentato da Il Sole 24 ore, dove si parla della matematica come di uno degli strumenti più equi nell’esercizio della democrazia. Ma per quanto sia equo, non riesce a evitare il paradosso, presentato da Marco Menale dalle pagine di MaddMaths! Si tratta del teorema di Kenneth Joseph Arrow, pubblicato nel 1957, che ci obbliga a notare che «l’unico sistema decisionale democratico sarebbe la dittatura». La conclusione, inevitabile, di Marco Menale è un po’ amara: «Ogni sistema di scelta maggioritario è in realtà un gioco non banale nel senso matematico, in cui la soluzione potrebbe non essere la migliore possibile, ma solo la meno sgradita ai più.»
Seconda giornata di prove orali: L'esame che vorrei
Quarta giornata di prove orali: L'esame che... sorprende
L'esame che vorrei
Il secondo giorno di prove orali dell’Esame di Stato non è stato meno ricco di spunti del primo.
Al primo candidato è stata proposta la raccolta di novelle Vita dei campi di Giovanni Verga: non ho trovato collegamenti tra Verga e la matematica (il che non esclude che ci siano), ma Verga viene sempre associato a Charles Dickens (e in effetti anche il candidato ha virato subito dopo sulla letteratura inglese). Nella ricerca di collegamenti tra Dickens e la matematica, mi sono imbattuta in un articolo di Brittany Carlson, dell’Università della California, che paragona il blocco dello scrittore all’ansia per la matematica, che spesso si esprime nel guardare impotenti un problema, senza riuscire a trovare un approccio. Nonostante la sua amicizia con Charles Babbage e Ada Lovelace, Dickens non aveva una buona opinione della matematica: nutriva un certo sospetto nei confronti di questa disciplina, soprattutto per l’uso che ne era stato fatto nelle statistiche, che avevano portato a deumanizzare e depersonalizzare i meno abbienti, appiattendo la situazione: la sua riprovazione è rivolta alle New Poor Laws del 1834, ma ha da ridire anche sull’educazione matematica, visto che non accettava che fosse insegnata, nel XIX secolo, usando la memorizzazione. Nella mia ricerca, ho trovato anche un articolo pubblicato sul numero 268 di Le Scienze, nel dicembre 1990, e riproposto nel 2012: è intitolato Il Teorema di Natale di Fermat ed è stato pubblicato nella rubrica L’angolo matematico di Ian Stewart. La lettura è davvero divertente: si tratta di un Canto di Natale modificato, con un Mister Stooge (=fantoccio) come protagonista (al posto di Scrooge=Tirchio), che incontra il Fantasma dei Teoremi del passato, il Fantasma delle Intuizioni future e il Fantasma delle Dimostrazioni presenti. Costellato da una serie di curiosità matematiche, a partire dai fattoriali e dai frattali, fino al “moduloscopio” che modifica i numeri, accarezza la Congettura di Fermat (nel 1990 non era ancora l’Ultimo Teorema), fino ad arrivare a Minkowski, alla relatività einsteiniana e alla “geometria dei numeri”.
Il secondo candidato si è visto proporre il romanzo Jane Eyre, di Charlotte Bronte, nel quale i temi sono l’amore, l’indipendenza e la figura della donna in epoca vittoriana. Ho trovato un articolo comparso sul numero 9 di Prisma, nel luglio 2019, scritto da Paola Magrone e Ana Millán Gasca, autrici del libro I bambini e il pensiero scientifico, che ha per protagonista Mary Everest Boole, una donna in epoca vittoriana. Moglie di George Boole e nipote di George Everest, «fece della ricerca della verità il filo conduttore della sua vita». Avrebbe potuto studiare matematica a Cambridge, ma, come sentì dire dal padre: «Che cosa può fare una ragazza studiando matematica?». È di fatto costretta a formarsi autonomamente, dimostrando una grande determinazione. Il marito dà un grande contributo al suo percorso, tributandole molta stima, come mostrato dalla lettera scritta ad Augustus de Morgan: «Non c’è assolutamente nessuna persona [in Irlanda] con cui io discuta di logica eccetto mia moglie». L’obiettivo di Mary Everest Boole era di formare i bambini al pensiero scientifico per avere adulti migliori, mostrando le difficoltà della scienza per farla amare, consapevole che una semplificazione eccessiva avrebbe annoiato i bambini, smorzandone la passione.
Il terzo documento è stato preso dal sito Our World in data e si tratta di una serie di tre grafici, proposti dagli economisti Branko Milanovic e Christoph Lakner, che mostra la storia della disuguaglianza economica globale. «Ciò che più conta per stabilire quanto tu sia sano, ricco e istruito, non è chi sei, ma dove sei», è dichiarato in apertura dall’autore dell’articolo Max Roser. I grafici mostrano una situazione di povertà nel 1800, che evolve in una grande disparità nel 1975, fino ad arrivare al 2015, quando l’estrema povertà è crollata come mai prima d’ora.
Il quarto collegamento è stato davvero inaspettato: si parla di letteratura spagnola, che non conosco molto, e protagonista è l’opera di Rafael Alberti. Prima ho trovato la poesia Alla divina proporzione, contenuta nella raccolta Poesie dell’esilio e dell’attesa, probabilmente scaturita dalla lettura della Divina proportione di Luca Pacioli del 1509. Si tratta di un sonetto che, come viene ribadito nel blog Literary, è la «forma poetica rinascimentale simbolo per eccellenza di perfezione metrica lucida e ragionata su parametri matematici non solo nel computo sillabico dell’endecasillabo, ma anche nello schema prosodico in seno a ogni verso». La cosa simpatica è che, letta nella lingua originale, presenta in apertura di strofa “A ti”, che crea un’assonanza con phi, il simbolo della sezione aurea. Cercando ulteriori conferme, sono approdata al blog di Marco Fulvio Barozzi, Popinga, che propone El ángel de los números, dalla raccolta Sobre los angeles del 1928, «in cui affiorano i ricordi di scolaro affascinato dal freddo suono del gesso sulla lavagna e dall’azione del cancellino sulle parole e sui numeri».
La mattinata si è davvero chiusa in bellezza con il documento che rimandava al celebre Ritratto di Dorian Gray di Oscar Wilde. Complice la citazione presente nella prova di matematica dell’Esame di Stato del liceo scientifico («Le forme create dal matematico, come quelle create dal pittore o dal poeta, devono essere belle: le idee, come i colori o le parole, devono legarsi armoniosamente. La bellezza è il requisito fondamentale: al mondo non c’è posto perenne per la matematica brutta!»), ho subito pensato al matematico Godfrey H. Hardy. Cercando sul web, mi sono imbattuta nel blog Robiland, che riporta una descrizione del matematico, stralciata dal libro di Robert Kanigel L’uomo che vide l’infinito, pubblicato nel 2003 per Rizzoli. In apertura del quarto capitolo, dedicato ad Hardy, Kanigel scrive: «Era oggetto di studio sull’eterna giovinezza. Un giorno della primavera del 1901, Hardy portò l’amico Lytton Strachey nel prato privato dietro il Trinity College, cui aveva accesso in quanto fellow del college, per una partita a bocce. “È il genio matematico per eccellenza” scrisse Strachey a sua madre “e ha l’aspetto di un bambino di tre anni.” Persino dopo aver superato i trent’anni, Hardy si vedeva spesso rifiutare la birra e almeno una volta, mentre pranzava con altri docenti del Trinity, venne scambiato per uno studente.» Direi che non potrebbe esserci esempio migliore, soprattutto perché L’apologia di un matematico (citata appunto nella seconda prova di matematica) permette una chiusura (di questo articolo) provocatoria: «La matematica greca è “perenne”, ancora più della letteratura greca. Archimede sarà ricordato quando Eschilo sarà dimenticato, perché le lingue muoiono ma le idee matematiche no. “Immortalità” forse è una parola ingenua, ma un matematico ha più probabilità di chiunque altro di raggiungere quello che questa parola designa.»
Prima giornata di prove orali: L'esame che farei
Terza giornata di prove orali: L'esame che amerei
L'esame che farei
Ogni volta che mi trovo ad assistere alla prova orale dell’Esame di Stato, succede la stessa cosa: quando si propone al candidato il documento che dovrebbe essere lo spunto del percorso pluridisciplinare, ogni insegnante ha chiaro in mente ciò che vorrebbe sentirsi dire per la propria disciplina. Quando, come me quest’anno, sei un commissario esterno nominato per matematica e informatica in un liceo linguistico, non hai grandi aspettative: i ragazzi possono fare quei collegamenti che sono stati abituati a fare e so che, messo di fronte alla scelta, l’insegnante di matematica in genere dà la precedenza ai contenuti disciplinari, in altre parole agli studi di funzione, e il candidato difficilmente si lancerà in collegamenti di spessore che non ha avuto modo di cogliere nel corso dell’anno. Ciò che intendo è che il collegamento resistenza partigiana – resistenza elettrica capita con una certa frequenza, anche se, in questo caso, declinato in ambito matematico. Perciò, nel momento in cui comincia la prova del candidato di turno, mi diverto a cercare quei collegamenti che mi piacerebbe sentirmi raccontare, spesso imparando un sacco di cose nuove nel frattempo, e creandomi l’opportunità, nel caso di difficoltà del candidato, di proporre un argomento in tema.
Il primo documento di oggi aveva a che fare con la Rivoluzione russa: il primo suggerimento di Google mi rimandava a Perel’man e alla congettura di Poincaré, ma l’ho ritenuto un po’ forzato, avendo in comune solo la nazionalità. Mi è piaciuta, invece, la storia di Igor Tamm, premio Nobel per la fisica nel 1958, raccontata da Pisani nelle pagine di MaddMaths! Già il titolo conquista: Igor Tamm e il calcolo che… salva la vita. Pisani racconta che, proprio durante la Rivoluzione russa, il fisico insegnava in Ucraina e, aggirandosi per un villaggio in cerca di cibo, un giorno si è imbattuto in un gruppo di banditi. Il capo della banda, una volta saputa la sua professione, gli ha chiesto di dargli «una stima dell’errore che si commette troncando uno sviluppo in serie di Mac Laurin all’n-mo termine». E ha aggiunto: «Fallo e sarai libero, fallisci e ti sparo». Fortunatamente Tamm non ha sbagliato!
Il secondo documento è stato più semplice: il protagonista era Nietzsche, ritratto da Munch, perciò ho googlato “Nietzsche e matematica” e mi sono imbattuta in un interessante articolo di Paolo Caressa, pubblicato sul numero di febbraio 2021 della rivista Prisma, Il teorema dell’eterno ritorno. «Il suo argomento per l’eterno ritorno è matematicamente sensato e si può ricondurre al fatto che, se f: X → Y è una funzione fra gli insiemi X e Y, con X infinito e Y finito, allora f non può essere biunivoca, cioè non può far corrispondere ciascun elemento di X a un solo elemento di Y», dove X è l’insieme degli infiniti istanti, mentre Y è l’insieme degli elementi di cui consta il mondo (ed è per forza un insieme finito). Anziché parlare di funzioni biunivoche, però, mi sono accontentata di fare riferimento alla circonferenza che rappresenta l’eterno ritorno, chiedendo se la circonferenza fosse una funzione…
La terza proposta era l’immagine di una trincea e richiamava, quindi, la Prima guerra mondiale. Devo dire che, in questo caso, ho trovato abbastanza semplice il collegamento, avendo parlato del ruolo degli scienziati tra le due guerre mondiali proprio in una serie di lezioni di educazione civica, proposte alla mia ultima quinta. Ho provato comunque a googlare e ho ritrovato l’articolo di Pietro Nastasi Un matematico alla grande guerra: Mauro Picone. Nell’articolo si parla dei calcoli per ricostruire delle tavole di tiro adeguate, visto che il lancio di granate avveniva in montagna, oltre alle enormi possibilità di calcolo della calcolatrice Brunswiga (e noi che pensiamo sempre e solo a Turing contro Enigma!), ma si parlava soprattutto del fatto che Mauro Picone è stato il fondatore dell’Istituto per le Applicazioni del Calcolo, che oggi porta, appunto, il suo nome. È un peccato che questa storia non sia stata raccontata agli studenti…
Il quarto argomento aveva a che fare con gli Organi dello Stato e in questo caso il riferimento immediato, almeno per quanto mi riguarda, era al libro di Chiara Valerio La matematica è politica. Il secondo riferimento, invece, ha a che fare con il fascismo: si tratta di Vito Volterra, matematico impegnato in politica, è stato senatore a partire dal 1905, ha contribuito alla Fondazione della SIPS, la Società Italiana per il Progresso delle Scienze, ma soprattutto ha rifiutato di prestare il giuramento di fedeltà al fascismo. La sua storia è ben raccontata nella graphic novel La funzione del mondo, che racconta la sua vita e la nascita della modellizzazione.
L’ultimo collegamento mi ha messo un po’ in difficoltà: si trattava di una citazione tratta da Notre-Dame de Paris di Victor Hugo che, per un caso fortuito, sto ascoltando in auto durante il viaggio per raggiungere la sede d’esame (160 km al giorno sono tanti…). Ho setacciato il web, ma non ho trovato nulla che collegasse l’opera del grande scrittore alla matematica. Mi sono imbattuta in un testo dell’Università degli Studi di Firenze, ma non sono riuscita a scaricarlo, perciò ho rimandato la ricerca. Rientrata a casa, sono stata in grado di aprire il pdf, e di scoprire che Hugo non aveva grande simpatia per la matematica, ma mi sono imbattuta anche in una versione pdf del romanzo. Una rapida ricerca mi ha permesso di verificare che la matematica viene citata solo due volte: «Quella zingara che sapete, quella che viene tutti i giorni a danzare sul sagrato, nonostante il divieto ufficiale! Ha una capra indemoniata con le corna del diavolo, che legge, scrive, conosce la matematica come Picatrix, e che basterebbe a far impiccare tutti gli zingari.» La seconda non è migliore, visto che Gringoire dice di aver «calcolato matematicamente la resistenza di quella castità alla seconda potenza». Inoltre, Victor Hugo non recupera nemmeno citando tre volte Pitagora: prima lo mette insieme a Nicolas Flamel e Zoroastro, poi lo indica come filosofo, e infine facendo dire a Jean du Moulin: «sarò un vero Pitagora di scienza e di virtù».
L’avventura tra letteratura e matematica per oggi si chiude qui, ma spero che domani le pagine di Gian Italo Bischi dedicate a Matematica e letteratura possano riservarmi citazioni più ottimistiche di quella di George Orwell (da “1984”): «Un bel giorno il Partito avrebbe proclamato che due più due fa cinque, e voi avreste dovuto crederci.»
Seconda giornata di prove orali: L'esame che vorrei
Verso il futuro
Durante tutto il processo di analisi dei dati, ci siamo resi conto di ciò che avremmo dovuto cambiare, in parte per semplificare il nostro lavoro e in parte per rendere ancora più attendibile la nostra indagine statistica, evitando ambiguità:
- prima di diffondere il sondaggio, potrebbe essere utile farlo compilare ad alcune persone, per valutare la chiarezza delle domande e poter, quindi, procedere con eventuali correzioni;
- formulare delle domande chiuse, semplici, chiare e senza una dubbia interpretazione per evitare errori da parte di chi deve compilare il sondaggio; ridurre il più possibile le risposte aperte per rendere più facile l’analisi dei dati;
- nel caso dell’impiego, inserire delle opzioni di risposta che consentano di ricondurre facilmente la professione alle categorie indicate dall’ISTAT;
- una domanda che abbia per risposta “spesso” o “qualche volta” risulta poco oggettiva: dovremmo precisare quanto è “spesso” dal nostro punto di vista (tutti i giorni? Più volte al giorno?).
Queste riflessioni si riveleranno particolarmente utili nel momento in cui procederemo alla stesura di un nuovo questionario, avente per oggetto la matematica nella quotidianità.
IL NUOVO QUESTIONARIO
Nell’ottica di mettere a frutto quanto imparato con questa indagine e con l’obiettivo di realizzare un nuovo questionario (che però verrà somministrato e analizzato da un’altra classe), ci siamo concentrati sulla presenza della matematica nella nostra vita quotidiana. Nel proporre il questionario non abbiamo potuto non tenere conto di alcuni aspetti legati anche all’ambito lavorativo, perché riteniamo che in qualche modo questo possa influenzare l’uso che se ne fa nel resto della giornata. È più probabile che ricorra alla matematica per la soluzione di problemi quotidiani un docente di matematica, ad esempio, rispetto a qualcuno il cui lavoro non ne prevede una grande applicazione. Per la formulazione delle domande, e soprattutto delle scelte multiple, abbiamo riflettuto sulle varie azioni e sui singoli momenti della giornata, per poter capire quanto la matematica sia parte della nostra vita. Abbiamo analizzato anche le diverse branche della matematica per capire quali potessero essere le loro applicazioni, chiedendo aiuto ad altre persone per arricchire la casistica, in modo anche da avere un’idea di quanto la gente possa essere consapevole delle applicazioni quotidiane.
Per le prime domande, ci siamo volute soffermare su due informazioni personali che abbiamo ritenuto importanti, ovvero il grado di istruzione e la fascia d’età, per poter valutare l’impiego della matematica in funzione del proprio titolo di studio. Per i quesiti successivi, ci siamo concentrate su richieste generali che ci aiuteranno a comprendere quanto la matematica sia riconosciuta dalle persone. La prima domanda è una versione quotidiana di quella proposta alla fine del precedente questionario: al posto di «Pensa che potrebbe lavorare senza matematica?», abbiamo proposto «Pensa che la sua vita sarebbe uguale se non ci fosse la matematica?», mentre la domanda successiva chiede di quantificare l’utilizzo della matematica nella quotidianità.
«Che cosa applica della matematica nel suo lavoro?» è diventata: «In quali attività utilizza di più la matematica?» e abbiamo proposto alcune risposte, collegando l’argomento matematico a un esempio tratto dalla quotidianità. Per trovare le possibili risposte a questa domanda e chiarire i dubbi che ci erano sorti, abbiamo chiesto ai nostri genitori e a conoscenti in quali attività ritenevano che questa disciplina fosse fondamentale: valutare le offerte al supermercato, gestire le finanze personali, modificare una ricetta per adeguarla al numero di persone usando le proporzioni… Tra le alternative possibili abbiamo messo anche i viaggi e lo sport, pensando ai fusi orari, al cambio monetario e alle combinazioni delle squadre durante i tornei.
Abbiamo ritenuto fosse il caso di chiedere con quale frequenza venga usata la calcolatrice per risolvere semplici problemi aritmetici, pensando alle ricette o alla suddivisione del conto in pizzeria, per riuscire a cogliere quanta dimestichezza abbiano le persone con la matematica.
Quella più bella, a nostro modo di vedere, è quella riguardante le differenti competenze matematiche a seconda del luogo in cui si vive: siamo consapevoli che esista una matematica diversa a seconda del contesto in cui si vive, basta confrontare tra loro una tribù indigena e un tipico abitante di New York e ci piacerebbe vedere quale potrebbe essere la risposta a questa domanda.
Ci sono anche tante altre domande, ma non è il caso di rovinarvi la sorpresa…
Conoscenze adeguate?
La domanda numero 6 del questionario ha a che fare con il bagaglio di conoscenze fornito dalla scuola: «La scuola che ha frequentato le ha fornito un bagaglio di conoscenze matematiche adeguato rispetto a quello che deve fare?». Le risposte a disposizione erano cinque:
- Non uso la matematica nel mio lavoro
- Per la matematica che uso, bastavano le elementari!
- Le conoscenze che ho NON sono adeguate: avrei dovuto fare un'altra scuola
- Le conoscenze che ho NON sono adeguate: avrei dovuto studiare di più
- Le conoscenze che ho sono adeguate
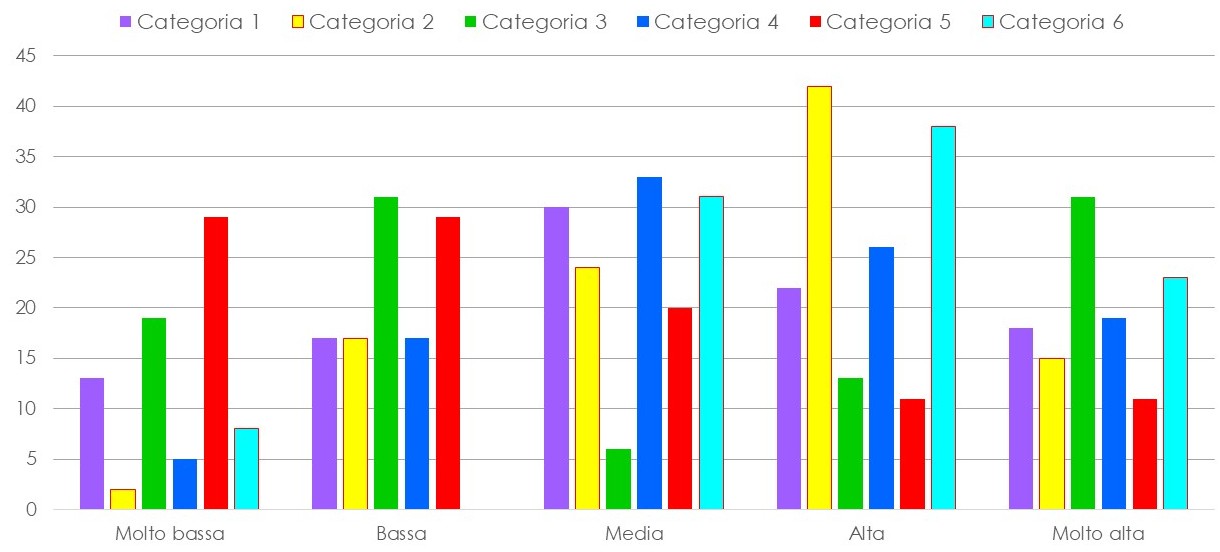
A queste 5 risposte è stato assegnato un punteggio da 1 a 5 a partire dalla prima, e poi è stata fatta la media per ricavare il grafico seguente.
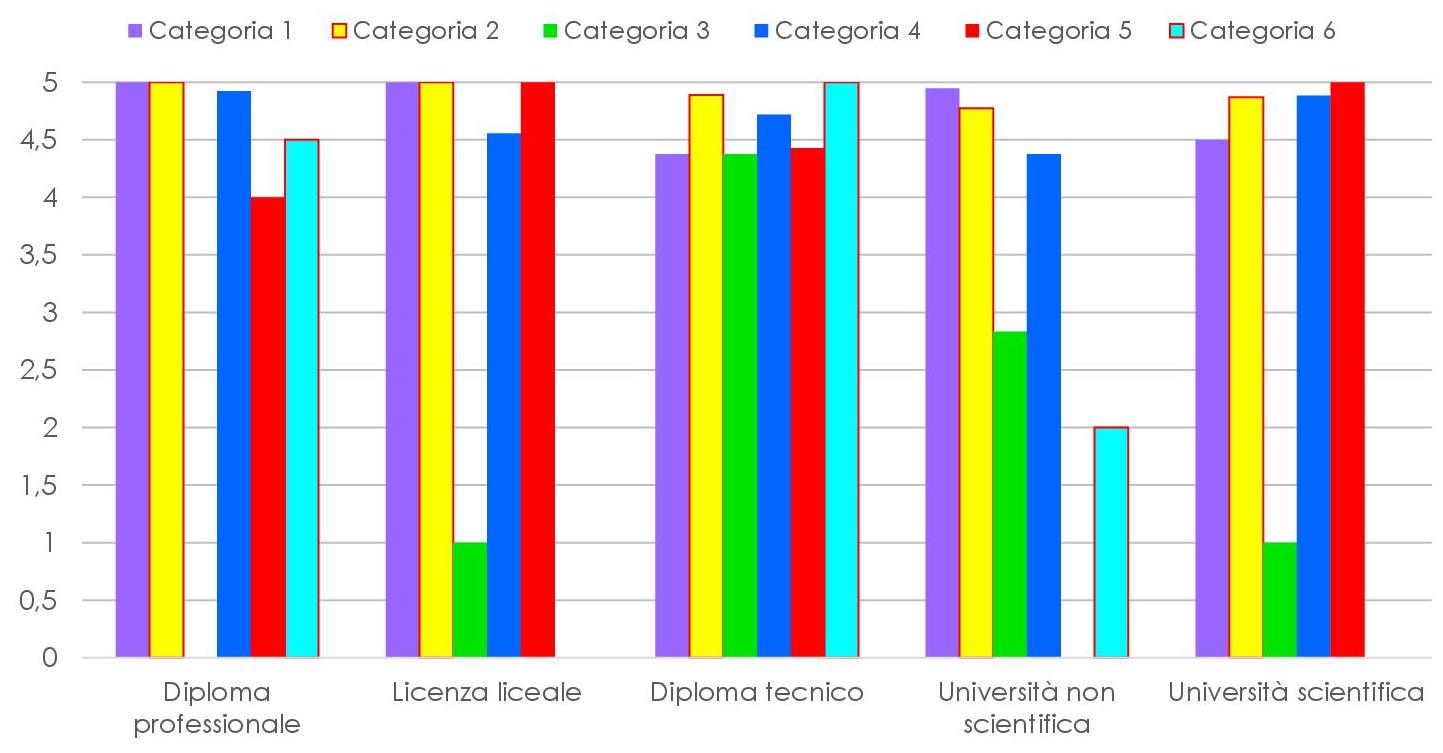
Cerchiamo di interpretarlo dando rilevanza al titolo di studio, riportato in ascissa, mentre i colori riportano l’attenzione sulle categorie. Prima di addentrarci nella descrizione, facciamo alcune precisazioni:
- il commento che segue non vuole essere un giudizio sulla scuola
- come evidenziato nel primo paragrafo, alcune professioni hanno visto un cambio di titolo di studio
- il livello di adeguatezza è percepito, non giudicato obiettivamente
- il percorso professionale scelto, come evidenziato nel paragrafo precedente, è stato fortemente influenzato dal proprio rapporto con la matematica
Analizziamo i risultati, usando due diversi raggruppamenti: prima consideriamo il livello scolastico e poi la categoria.
- Diploma professionale: coloro che hanno risposto al questionario si riconoscono una preparazione matematica adeguata al percorso scelto. Questo potrebbe rispecchiare la realtà delle scuole professionali, dove si addestrano gli studenti a svolgere lavori più che altro pratici, che non richiedono grandi competenze matematiche.
- Licenza liceale: spicca la colonna della terza categoria: si tratta di un’unica risposta, data da un’educatrice, che dichiara di non usare la matematica nel proprio lavoro. Al netto di questa risposta, possiamo dire che la licenza liceale dà competenze matematiche adeguate.
- Diploma tecnico: gli istituti tecnici forniscono conoscenze matematiche adeguate al lavoro per la maggior parte dei propri studenti. Questo potrebbe restituirci il quadro di una scuola che istruisce i propri studenti con competenze matematiche specifiche per il lavoro che dovranno affrontare.
- Università non scientifiche: sembra che le categorie 3 e 6 siano quelle più problematiche: per la categoria 3, le lauree non scientifiche corrispondono a sei educatrici, che hanno risposto come segue: due hanno dichiarato di avere conoscenze matematiche adeguate, una ha risposto di non usare la matematica nella sua professione e tre hanno dichiarato di usare la matematica elementare. Per la categoria 6, si tratta di un’operaia agricola, che dichiara sufficiente la matematica elementare per il suo lavoro.
Se consideriamo il risultato nel suo complesso, possiamo notare che la maggior parte dei laureati sostiene di possedere conoscenze matematiche adeguate al mondo del lavoro, mentre per gli altri, vale il fatto che il percorso scolastico non dà rilevanza alla matematica, che effettivamente non sempre viene usata sul fronte professionale. - Università scientifica: sembra che le conoscenze siano adeguate, tranne che per la categoria 3: si tratta di un’educatrice che ha dichiarato di non usare la matematica nel suo lavoro. Per il resto non ci sono grandi sorprese: è forse scontato ritenere che le facoltà scientifiche preparino gli studenti in maniera adeguata dal punto di vista matematico, ma è bello vederlo confermato dal nostro campione.
Concentrandoci sui colori, ovvero sulle singole categorie, possiamo avere un diverso punto di vista:
- Categoria 1: il primo gruppo comprende avvocati, dirigenti e imprenditori. I ruoli dirigenziali richiedono competenze matematiche, che coinvolgono il processo decisionale, l’analisi dei dati e la lettura dei grafici, mentre per quanto riguarda gli avvocati, è altro ad avere più peso. Il grafico ci dice che chi appartiene a questa categoria ritiene di avere competenze matematiche adeguate.
- Categoria 2: si tratta di consulenti, ingegneri, medici e commercialisti e il grafico evidenzia che tutti coloro che hanno risposto al questionario ritengono di avere competenze matematiche adeguate.
- Categoria 3: al nostro questionario hanno risposto principalmente educatrici e agenti di commercio. In entrambi i casi, si tratta di professioni basate più che altro su competenze relazionali, perciò le competenze matematiche non sono molto richieste o basta la matematica elementare.
- Categoria 4: gli impiegati che hanno risposto al nostro questionario si riconoscono competenze matematiche adeguate.
- Categoria 5: a parte il caso dell’operaia agricola richiamata sopra, a questa categoria appartengono diplomati che per la maggior parte dichiarano di avere competenze matematiche adeguate.
- Categoria 6: si parla di artigiani e operai specializzati, che dichiarano di avere competenze matematiche adeguate.
Concludi con le Prospettive future
Il rapporto con la matematica
Nella stesura del questionario, abbiamo ritenuto importante indagare anche il rapporto dei partecipanti con la matematica e, suddividendo le loro risposte in base al grado di istruzione, abbiamo potuto trarre alcune conclusioni che, per quanto limitate al campione esaminato, sono interessanti e permettono alcune riflessioni di più ampio respiro.
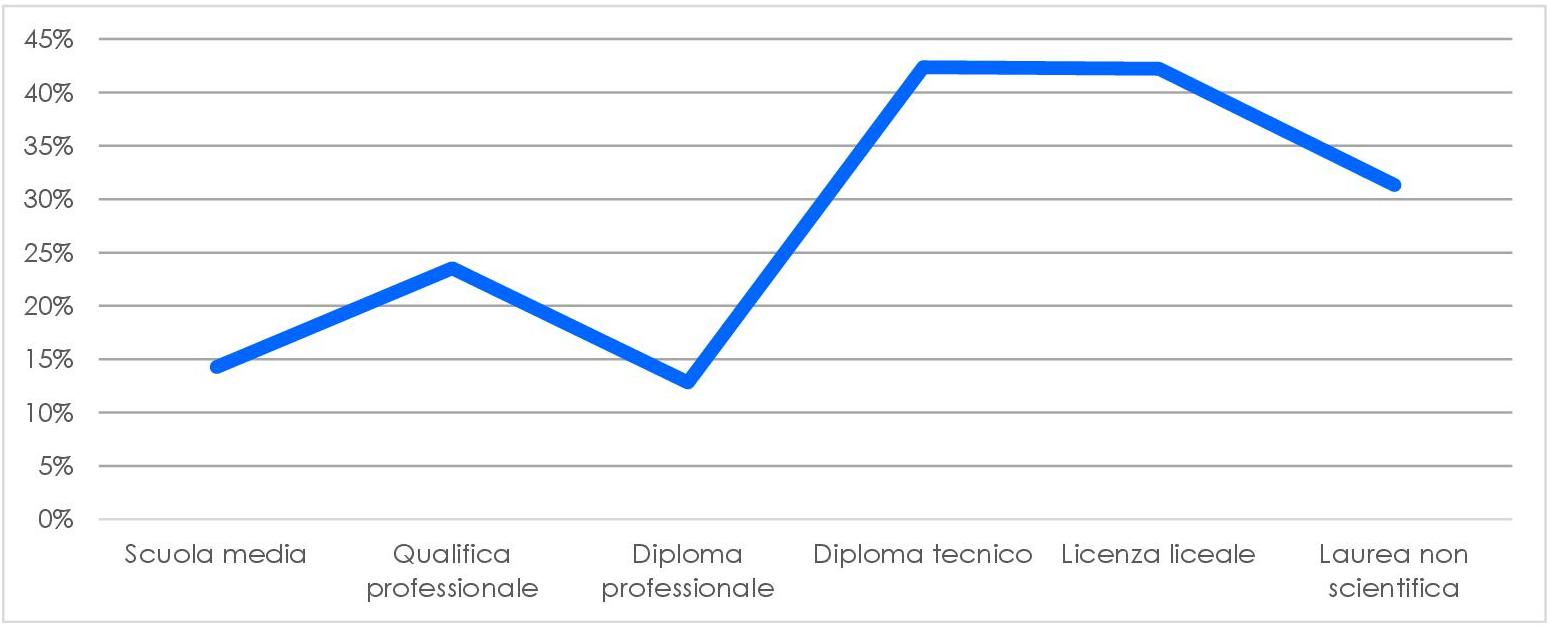
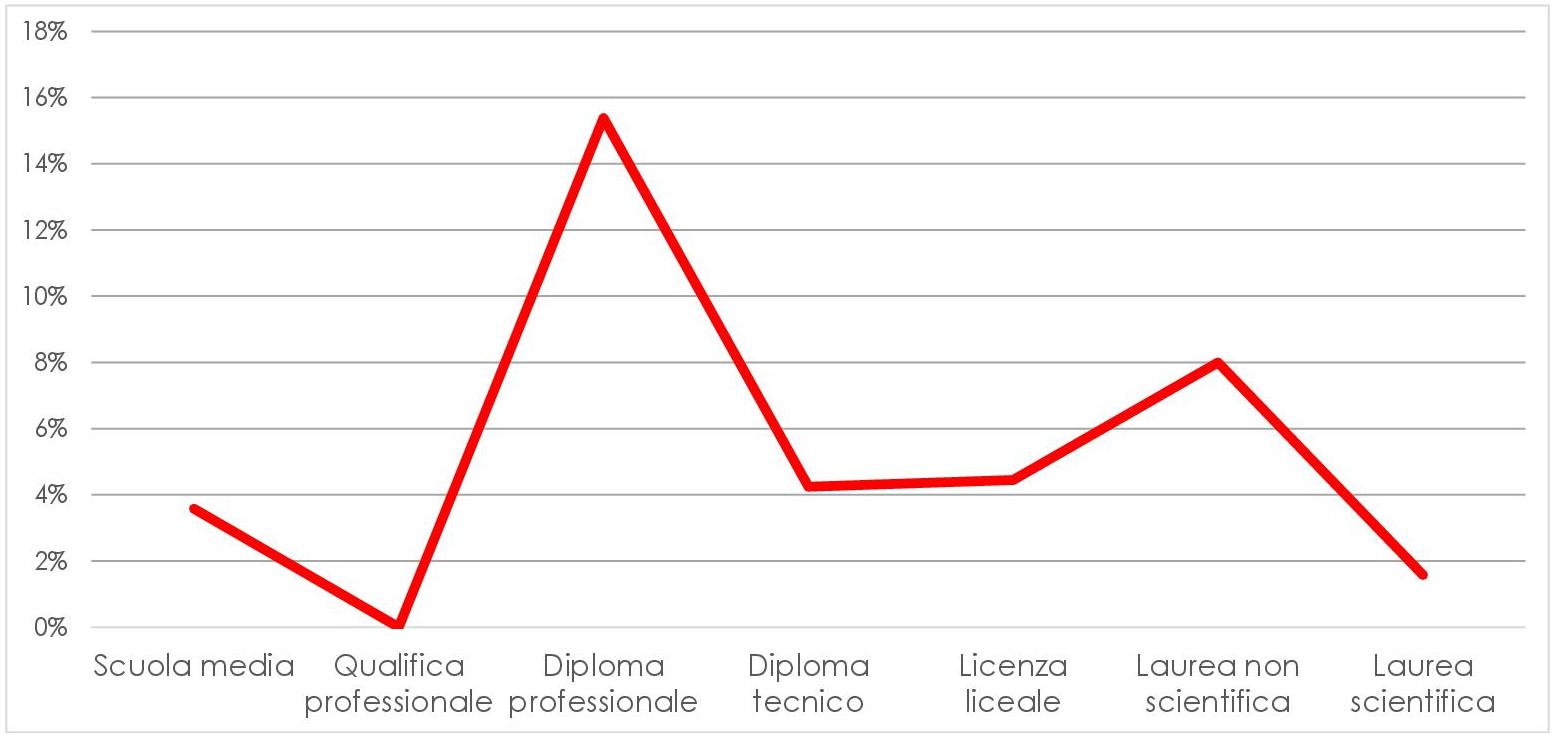
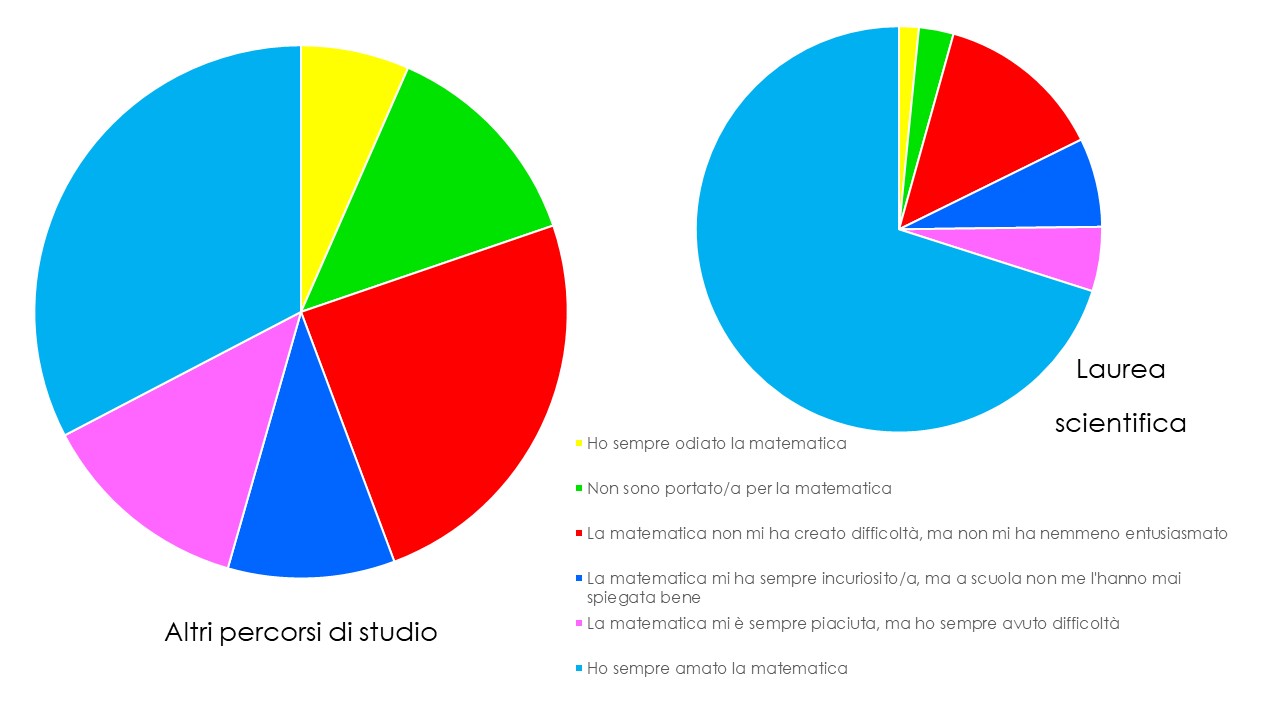
I due grafici precedenti si riferiscono all’amore (in blu) e all’odio per la matematica: tra i nostri intervistati, chi ha scelto di non proseguire gli studi dopo la scuola secondaria di primo grado ha avuto maggiori difficoltà in matematica e, in alcuni casi, ha sviluppato un sentimento negativo per la disciplina. Sorprendentemente, sulla totalità del campione solo il 5% ha dichiarato di odiare la matematica, mentre quasi la metà ha ammesso di averla sempre amata e molti hanno affermato di esserne stati affascinati o incuriositi. Questo ci ha portato a interrogarci sulle risposte raccolte e abbiamo dedotto che le risposte sono arrivate, di preferenza, da chi già aveva un sentimento positivo per la matematica: a parte i nostri contatti diretti, scelti tra i nostri genitori e gli amici dei nostri genitori, che hanno scelto di rispondere perché gliel’abbiamo chiesto noi, gli altri intervistati non sono stati scelti tra gli utenti dei social in generale, ma tra quelli che hanno già un rapporto positivo con la materia. Infatti, il questionario è stato condiviso dagli appassionati di matematica sui gruppi a tema matematico. Per questo motivo, per quanto il risultato possa essere più variegato quando si considerano altri percorsi di studio, rispetto alla laurea scientifica, anche in questo caso il nostro risultato non è attendibile: presenta una visione forse troppo rosea della realtà!
Non sorprende che chi ha conseguito una laurea scientifica abbia avuto un rapporto positivo con la matematica lungo il percorso, visto che il 60% degli intervistati ha dichiarato di essere stato influenzato nelle proprie scelte (scolastiche e lavorative) dal rapporto che ha avuto con la matematica. È per questo motivo che dal grafico che segue abbiamo dovuto escludere i laureati in materie scientifiche: l’elevata percentuale di amore per la matematica (70%) falsava la scala del grafico, appiattendolo, e rendendo, quindi, più difficile vedere le differenze tra le risposte dei singoli gruppi.
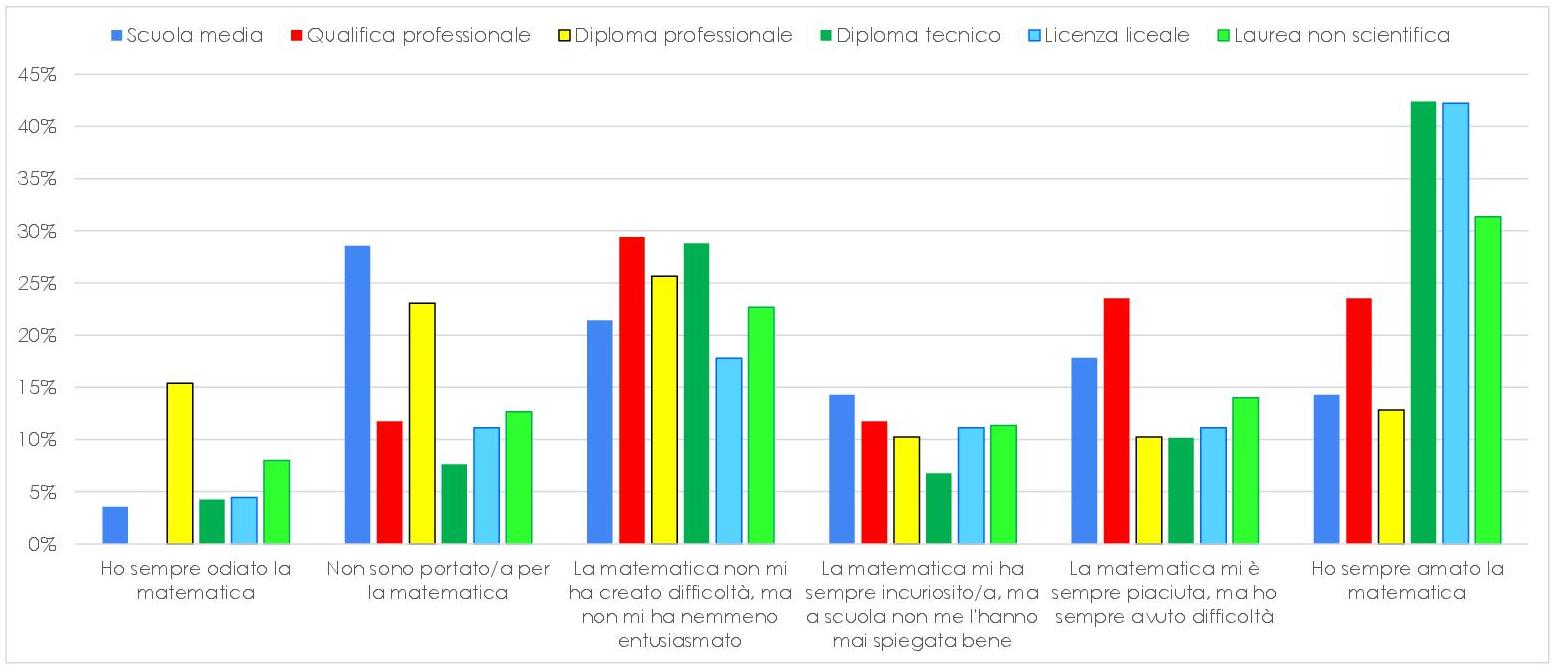
I SENTIMENTI DEI DOCENTI
Visto che tra i partecipanti all’indagine c’è un numero importante di insegnanti con laurea scientifica (86 questionari, corrispondenti al 13% degli intervistati), abbiamo deciso di analizzare in particolare il rapporto che essi hanno dichiarato di avere con la matematica e oltre ad aver raccolto 63 dichiarazioni di amore incondizionato per la materia, «Ho sempre amato la matematica», le risposte sono state un po’ più articolate, come se le possibilità concesse dal questionario non fossero adeguate ad esprimere la complessità del sentimento generato dalla matematica.
Oltre a quelli che hanno scelto più opzioni tra quelle proposte, qualcuno ha aggiunto particolari personali, a dimostrazione del fatto che la matematica genera sentimenti che coinvolgono il vissuto e che riconoscono addirittura una data all’inizio di questo amore: «Ho iniziato ad amare la matematica alle superiori grazie alla mia insegnante che ho avuto per tutti i cinque anni», «Ho iniziato ad amare la matematica dopo un'illuminazione ricevuta in seconda Liceo Scientifico», «Quando andavo a scuola non la amavo seppur non abbia mai avuto difficoltà. Poi qualcosa è cambiato!». Un altro commento rimanda a un rapporto con la matematica che non può che essere la traduzione di un rapporto con le persone, soprattutto alla primaria: «Ho sempre amato la matematica, ma me l'ha insegnata veramente bene solo la maestra; poi, un pochino, la professoressa delle medie; poi il nulla...», o come dichiarato da persone con altro titolo di studio: «La matematica mi piaceva, ma la professoressa era odiosa e quindi pure la matematica!». Per qualcuno questo amore ha rischiato di finire con l’esperienza universitaria: «Non mi ha entusiasmato lo studio universitario, tranne qualche esame, perché troppo teorico e nozionistico. Preferivo l'approccio più problematico, ragionato e applicativo del liceo scientifico», anche se abbiamo trovato un ingegnere che ha riportato un’esperienza opposta: «Ho scoperto la bellezza della matematica all’università. Fino alle superiori non mi è mai stata spiegata con passione da professori il cui unico obbiettivo era completare superficialmente il programma scolastico senza alcun amore per la professione dell’insegnante». Qualcuno, infine, dichiara un amore tardivo: «La matematica mi ha sempre affascinato e mi è sempre risultata piuttosto facile a scuola, però l’ho sempre studiata più per dovere che per passione finché ero studente».
Analizzando le risposte al nostro questionario, non è stato possibile individuare una professione con un vero odio per la matematica: in 34 questionari abbiamo registrato la risposta «Ho sempre odiato la matematica» e in 58 «Non sono portato/a per la matematica», ma non c’è una professione più presente di altre. Due sole sono le professioni che, in qualche modo, spiccano per una maggiore frequenza: quella degli impiegati (19 risposte in totale) e quella degli insegnanti (20 risposte). Questo non è sufficiente per dire che le due categorie sono "responsabili" di un sentimento particolarmente negativo per la disciplina, perché le due categorie spiccano anche nel sentimento opposto: semplicemente, siccome è elevato il numero di impiegati e di insegnanti intervistati, non possono che spiccare.
Tra le più belle risposte, non possiamo non segnalare quella di un’insegnante di religione di più di sessant’anni: «Subisco il fascino della matematica, riconosco che va avvicinata con creatività, penso che ci avvicini all'Infinito, ma so anche di non essere capace di inoltrarmi nella sua conoscenza». E questo solleva un importante tema, che ritorna più volte nelle risposte: non è l'odio il sentimento che ha raccolto il maggior numero di risposte, ma la sensazione di non essere portati per la matematica, il senso di inadeguatezza, o forse un facile alibi.
I SENTIMENTI DIVISI PER CATEGORIE PROFESSIONALI
Utilizzando la divisione per categorie di lavoratori come nel precedente paragrafo, abbiamo suddiviso le risposte in merito ai sentimenti della matematica.
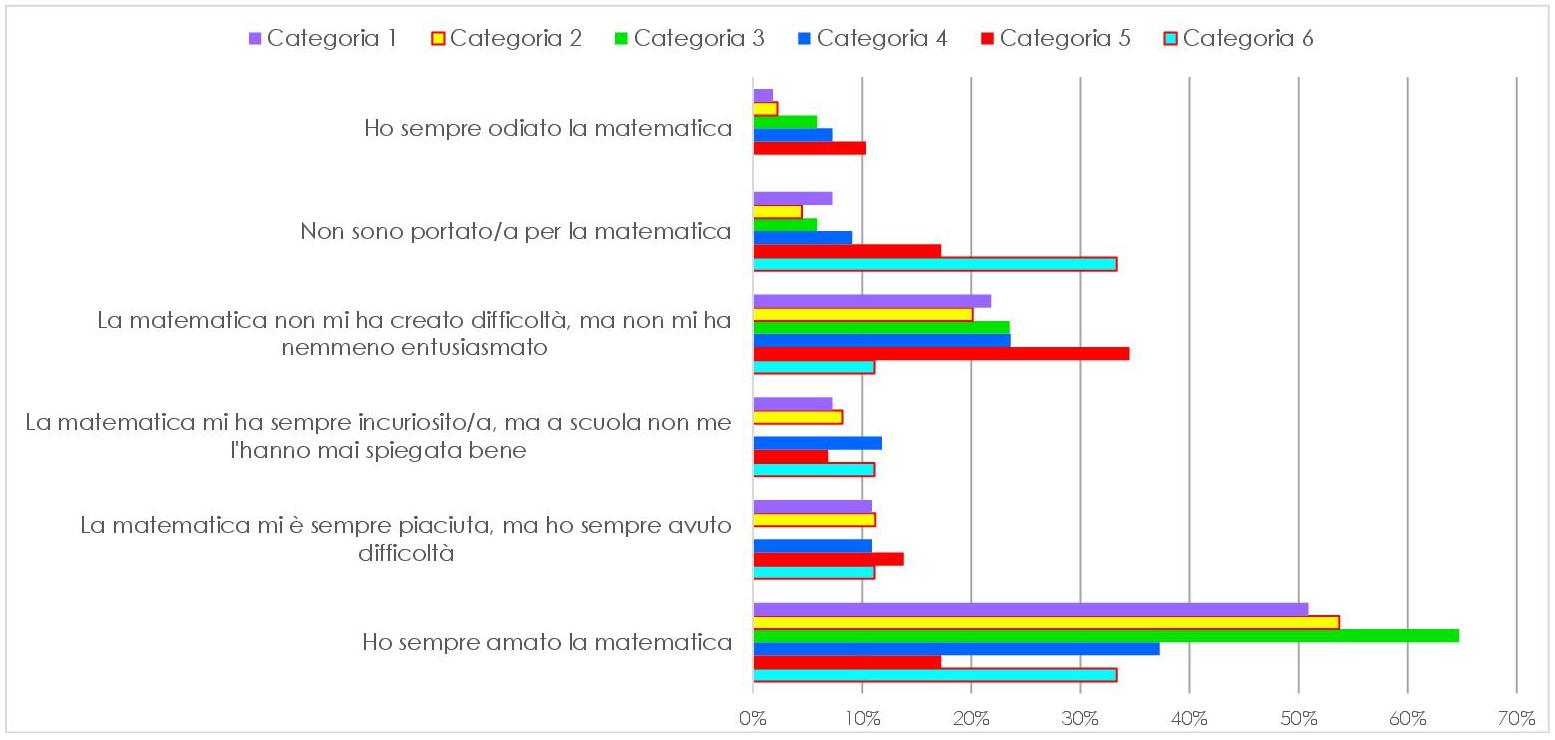
Quanto evidenziato dal grafico dà un’ulteriore conferma a quanto affermato precedentemente e, al tempo stesso, mostra come il riconoscimento dell’applicazione della matematica nelle proprie mansioni vada di pari passo con i sentimenti positivi che si possono nutrire per la disciplina. In alcune professioni, si sono rilevati risultati contraddittori in merito all’utilizzo della matematica, perché pur facendo lo stesso lavoro qualcuno ne ha riconosciuto la presenza e l’utilità, a fronte di altri che hanno dichiarato, quasi con spavalderia, di poterne fare a meno.
Prosegui con Conoscenze adeguate?
Matematica e mondo del lavoro
Per capire quanto la matematica sia presente nel mondo del lavoro, è stato necessario procedere con un raggruppamento delle professioni in alcune categorie, secondo la Nomenclatura e classificazione delle Unità Professionali dell’ISTAT, escludendo quelle risposte che non ci hanno fornito una risposta precisa o utile ai fini del sondaggio in questione come:
- pensionati, disoccupati e studenti: non è stato possibile associare loro una professione;
- liberi professionisti: si inseriscono in un ambito lavorativo molto vario e generico, difficile da classificare;
- insegnanti: l’insegnamento abbraccia molteplici e diverse discipline e spesso non è specificato il grado di scuola. Inoltre, l'elevato numero di questionari avrebbe falsato l'esito dell'indagine.
Le categorie risultanti sono sei:
- Categoria 1: legislatori, imprenditori e alta dirigenza (avvocati, direttori, dirigenti, manager, imprenditori, responsabili) Il primo grande gruppo, secondo l’ISTAT, «comprende le professioni che richiedono un livello di conoscenza necessario a definire e implementare strategie di indirizzo e regolazione in ambito politico, istituzionale ed economico, anche avvalendosi di contributi specialistici».
In questa categoria, abbiamo raccolto 55 questionari e tra di essi solo 9 dichiarano di poter svolgere il proprio lavoro senza la matematica. La maggior parte di chi ha risposto ritiene che la matematica faciliti il proprio lavoro, soprattutto gli imprenditori (74%), che sono gli unici a non aver risposto di poter fare a meno della matematica.
- Categoria 2: professioni intellettuali, scientifiche e di elevata specializzazione (data scientist, ingegneri, consulenti, architetti, psicologi, bibliotecari, ricercatori, informatici, infermieri, farmacisti, commerciali, commercialisti, medici e fiscalisti). «Il secondo grande gruppo comprende le professioni che richiedono un elevato livello di conoscenza teorica per analizzare e rappresentare, in ambiti disciplinari specifici, situazioni e problemi complessi, definire le possibili soluzioni e assumere le relative decisioni. I loro compiti consistono nell’arricchire le conoscenze esistenti.»
In questa categoria, abbiamo raccolto 134 questionari e tra di essi abbiamo la maggioranza assoluta della risposta «il mio lavoro non esisterebbe senza matematica». Anche osservando il grafico più dettagliato, possiamo concludere che tutte le professioni necessitano della matematica.
- Categoria 3: professioni tecniche (geometri, educatrici, agenti commerciali e un pilota di linea). «Il terzo grande gruppo comprende le professioni che richiedono conoscenze tecnico-disciplinari per selezionare e applicare operativamente protocolli e procedure definiti e predeterminati in attività di produzione o servizio. I loro compiti consistono nel coadiuvare gli specialisti in ambito scientifico, sanitario, umanistico, economico», sociale e produttivo.
In questa categoria, abbiamo raccolto 17 questionari, ma la maggior parte (11) è stata compilata da educatori, falsando quindi il risultato. Geometri, agenti di commercio e piloti non avrebbero un lavoro senza la matematica. Se analizziamo anche gli argomenti in gioco, scopriamo che gli educatori usano solo nozioni di calcolo aritmetico, mentre gli altri professionisti – i geometri in particolare – fanno uso non solo di grafici, ma anche di teoremi di geometria.
- Categoria 4: professioni esecutive nel lavoro d’ufficio (impiegati). La quarta categoria «comprende le professioni che svolgono il lavoro d’ufficio con funzioni non direttive. I loro compiti consistono nell’acquisire, trattare, archiviare e trasmettere informazioni […] e nella verifica e corretta applicazione di procedure».
In questa categoria, abbiamo raccolto 110 questionari e a parte 8 risposte, tutte le altre riconoscono la matematica come fondamentale nel proprio lavoro. Come indicato dall’ISTAT, le attività svolte consistono nell’amministrazione del personale, nel gestire la circolazione del denaro, nell’effettuare calcoli e rendicontazioni statistiche, e, per questo motivo, la maggior parte degli impiegati non può che riconoscere che senza matematica non avrebbe un lavoro.
Questa categoria, per la quale abbiamo realizzato un unico grafico visto che comprende un’unica figura professionale anche se dalle attività diversificate, rappresenta circa un sesto dei questionari analizzati: non è un caso, visto che le figure indagate lavorano nel settore terziario, che è uno dei settori più sviluppati in Italia.
- Categoria 5: professioni qualificate nelle attività commerciali e nei servizi (hair-stylist, pasticceri, commesse e commercianti). «Il quinto grande gruppo classifica le professioni che assistono i clienti negli esercizi commerciali, forniscono servizi di ricezione e di ristorazione, servizi ricreativi e di supporto alle famiglie, di cura della persona, di mantenimento dell’ordine pubblico, di protezione delle persone e della proprietà».
In questa categoria, abbiamo raccolto 29 questionari, dei quali 10 tra le casalinghe, che dichiarano, in buona parte, di poter fare a meno della matematica, o di poterlo fare con un po’ di fatica. Per i commercianti, le commesse, e l’unico pasticcere intervistato, la matematica è presente e davvero importante per il lavoro.
- Categoria 6: artigiani, operai specializzati e agricoltori (falegnami e operai). «Il sesto grande gruppo comprende le professioni che utilizzano l’esperienza e applicano la conoscenza tecnico-pratica dei materiali».
Tra i 9 questionari raccolti ci sono 8 operai e un falegname: per gli operai metalmeccanici la matematica è importante, come pure per il falegname, mentre tra gli altri operai due affermano di poter fare a meno della matematica.
Tra le risposte che ci sono pervenute, c’erano anche tre poliziotti, che abbiamo inserito nella categoria 5, perché sarebbe stato poco significativo considerarli nella loro categoria di appartenenza (la 9); non abbiamo trovato nessuno né per la categoria 7 né per la 8, anche se alcuni elementi – pochi – avrebbero potuto essere inseriti in queste. Abbiamo preferito ridurre tutto a sei categorie per rendere più facile lo studio.
Osservando i dati raccolti, ci rendiamo conto ora che la nostra indagine avrebbe dovuto cominciare dalla scelta degli intervistati: avremmo dovuto puntare ad avere lo stesso numero di elementi in tutte le categorie, ma la verità è che tutto è cominciato come una piccola indagine tra i nostri conoscenti e mai avremmo pensato di dover analizzare tanti questionari. Fin dall'inizio abbiamo riconosciuto che il nostro campione non è statisticamente rappresentativo, ma a noi è bastato per gettare uno sguardo sul mondo del lavoro e sul ruolo della matematica al suo interno.
QUALE MATEMATICA?
Calcolo aritmetico, algebra, calcolo delle probabilità e statistica, lettura dei grafici, teoremi di geometria e trigonometria, analisi e logica sono le parti della matematica più usate nelle varie professioni e, come è evidente dal grafico, ogni professionista necessita di matematica, per poter svolgere al meglio la propria mansione.
Come era prevedibile, il calcolo aritmetico è quello più usato da tutte le categorie: è indispensabile, non solo in termini di addizioni e sottrazioni. Tendiamo a classificare come “banale” calcolo aritmetico tutta quella matematica che ci pare semplice, ma sappiamo che anche il calcolo di una percentuale, per quanto comporti la soluzione di una semplice proporzione, non è così scontato. La lettura di grafici diventa determinante nell’ambito decisionale, come dimostrato dalle risposte delle categorie dirigenziali, mentre l’uso dei teoremi di geometria non è limitato alla categoria degli ingegneri e dei geometri, perché anche il falegname può averne bisogno.
Tra le risposte, ci ha colpito molto quella di una data scientist: "calcolo aritmetico, statistica, lettura di grafici, trigonometria (una sola volta, ma fu determinante)". Questa risposta ci ha fatto riflettere: nessuno di noi può sapere cosa sarà utile, di ciò che studiamo oggi, nel mondo del lavoro, ma tutto potrebbe essere utile, o addirittura necessario, "determinante". Non abbiamo ancora le idee chiare sulle nostre scelte lavorative, ma in ogni caso, nemmeno questa data scientist avrebbe potuto immaginare che avrebbe avuto bisogno della trigonometria!
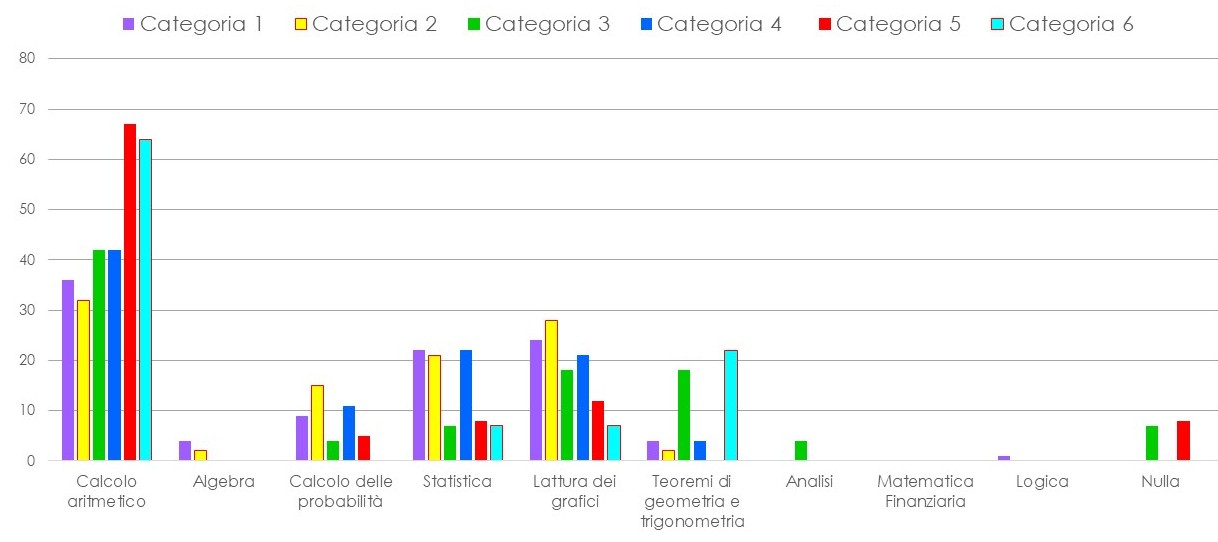
In conclusione, possiamo affermare che nonostante l’utilizzo delle diverse parti della matematica fatto dalle diverse professioni sia abbastanza diversificato e sia specifico, a volte, per alcune mansioni, tutte le professioni fanno uso di matematica.
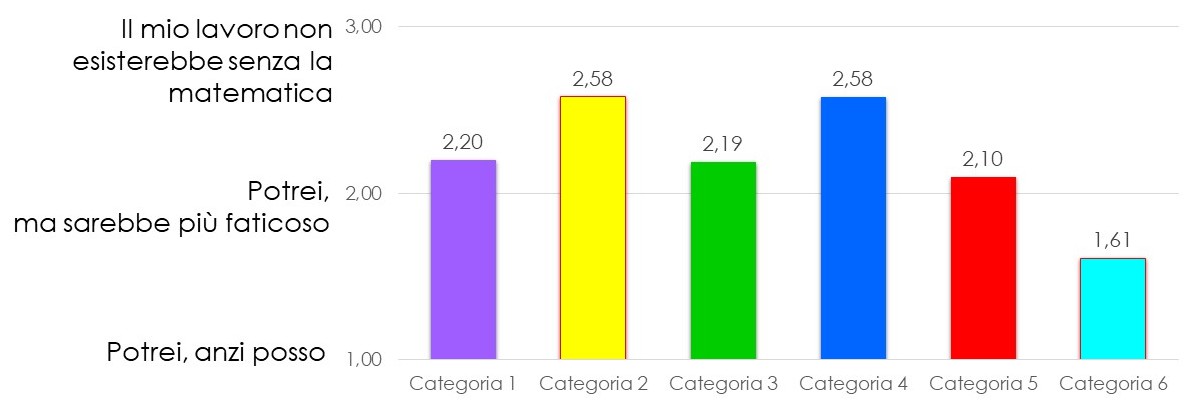
QUANTO È IMPORTANTE LA MATEMATICA NEL MONDO DEL LAVORO?
Per analizzare l’importanza della matematica nel mondo del lavoro, facciamo riferimento alla domanda 8 e facciamo una media dei valori assegnati da ogni intervistato. Riportati i risultati in un grafico, possiamo notare come la categoria 5, formata da 29 persone che compiono lavori pratici, sia quella che dà meno importanza alla matematica, facendone un utilizzo, per certi aspetti, più limitato. Per quanto riguarda la categoria 3, secondo risultato partendo dal basso, abbiamo già riconosciuto che la mescolanza delle professioni tecniche ha generato dei risultati un po’ bizzarri.
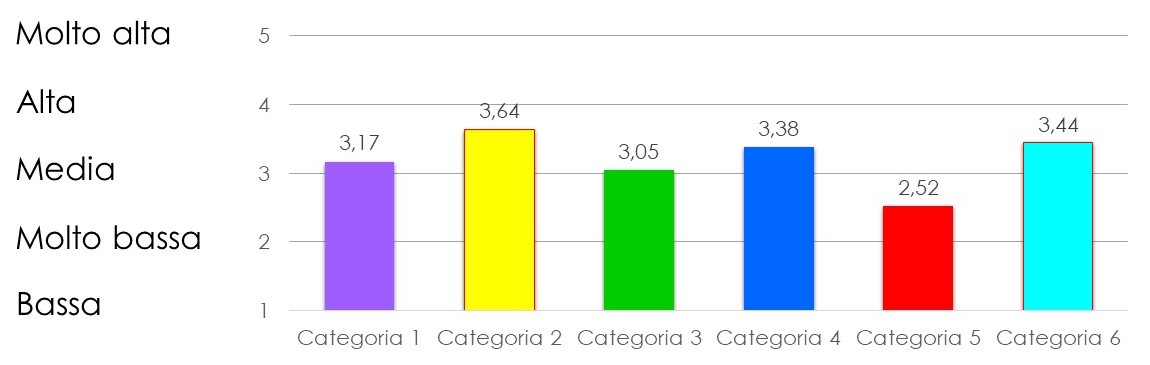
Rispetto alle domande analizzate in precedenza, possiamo rilevare una certa coerenza, tranne che per le categorie con il più basso numero di questionari: in questo caso, anche una singola risposta può incidere significativamente sui risultati medi.
Dall’analisi dei dati, possiamo dedurre che:
- La matematica è presente in tutti gli ambiti lavorativi;
- Gli strumenti matematici utilizzati sono condivisi da tutte le categorie, visto che solo alcuni settori particolari usufruiscono di metodologie logico-matematiche più settoriali;
- Chi potrebbe fare a meno della matematica si ritroverebbe con un lavoro più pesante e faticoso
- Abbiamo anche notato alcune incongruenze: in alcuni casi, pur svolgendo la stessa identica professione, è stato segnalato un uso diverso della matematica: a seconda della formazione della persona in questione (ad esempio: al livello dirigenziale si può accedere sia con una laurea scientifica che con una laurea non scientifica) è stata riconosciuta una presenza o un'assenza di matematica. In altre parole, parafrasando una celebre citazione: la matematica è negli occhi di chi guarda.
Prosegui con Il rapporto con la matematica
Profilo dei partecipanti
FONTI
In base al modo in cui i partecipanti hanno avuto accesso al questionario, possiamo distinguere tre categorie:
- 3AS: i partecipanti sono stati contattati personalmente dagli alunni della classe o dall’insegnante, tramite WhatsApp
- Social: i partecipanti hanno avuto accesso al link condiviso sui social (Instagram e Facebook)
- Contatti di contatti: chi ha ricevuto il questionario dagli alunni della classe ha poi contribuito a diffondere ulteriormente il questionario, inviandolo ai propri contatti
La maggior parte delle risposte (313) ci è pervenuta tramite nostri contatti diretti; le restanti risposte si suddividono quasi equamente tra social (172) e conoscenti dei nostri contatti (189).
È necessario, quindi, fare un paio di premesse:
- La nostra inesperienza nel porre le domande, combinata con l’accesso al questionario tramite i social, ha generato alcuni malintesi e alcune risposte sono, quindi, assenti o vaghe
- «Per essere attendibile, un campione deve essere rappresentativo della popolazione, ossia deve riprodurre su scala ridotta gli stessi dati rilevati per l’intera popolazione»[1]. È evidente che il nostro campione non può essere considerato rappresentativo della popolazione, visto come sono state raccolte le risposte. Evidenzieremo meglio la cosa proseguendo e confrontando i nostri dati con quelli rilevati dall’ISTAT.
GENERE ED ETÀ
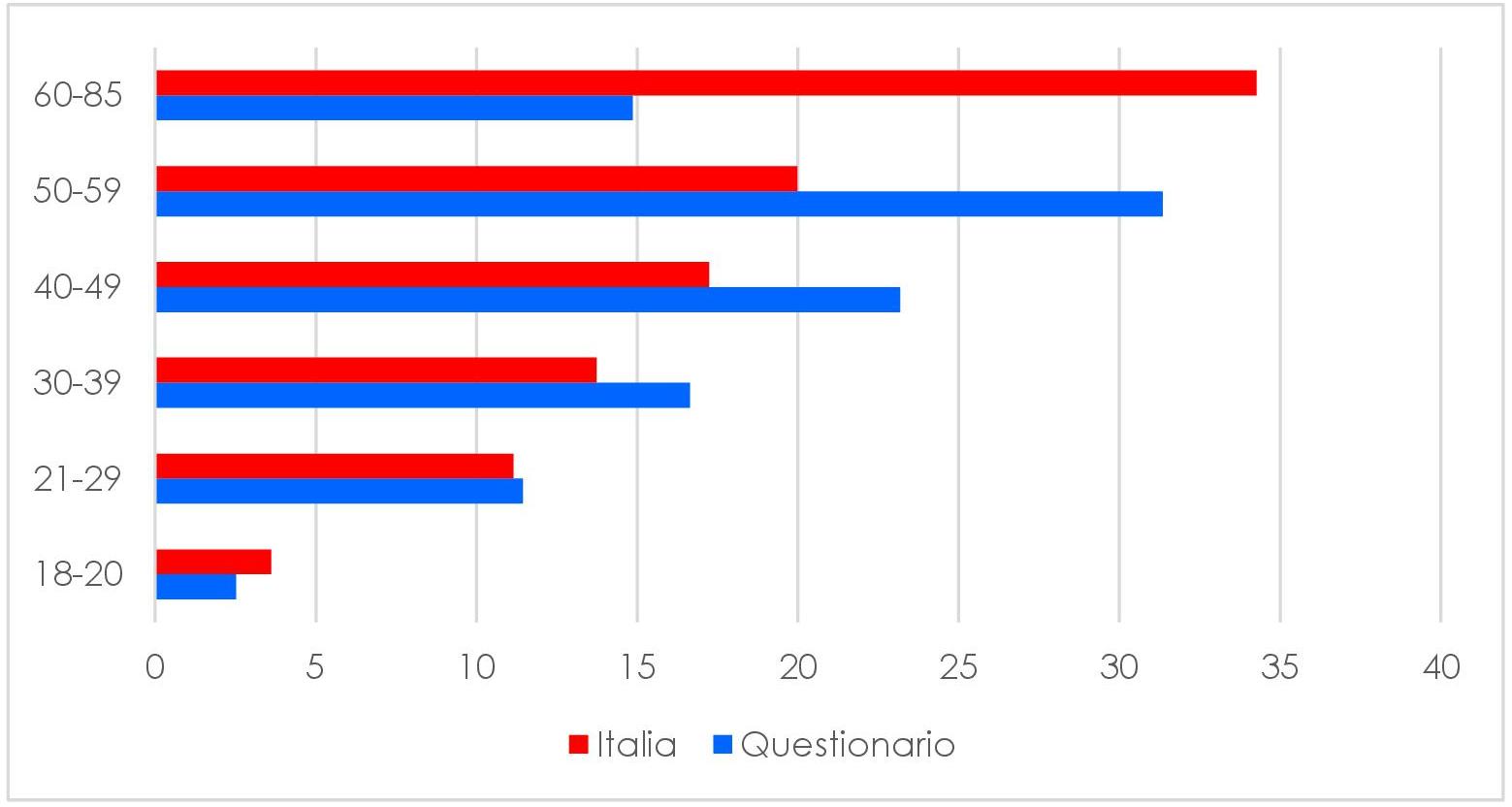
Analizzando le risposte (674 in totale), abbiamo cercato di ricostruire il profilo di coloro che hanno partecipato al sondaggio, focalizzandoci sul genere, l’età e il grado di istruzione. Il 59% dei partecipanti era costituito da donne e le età sono indicate nel grafico seguente e suddivise in base al genere:
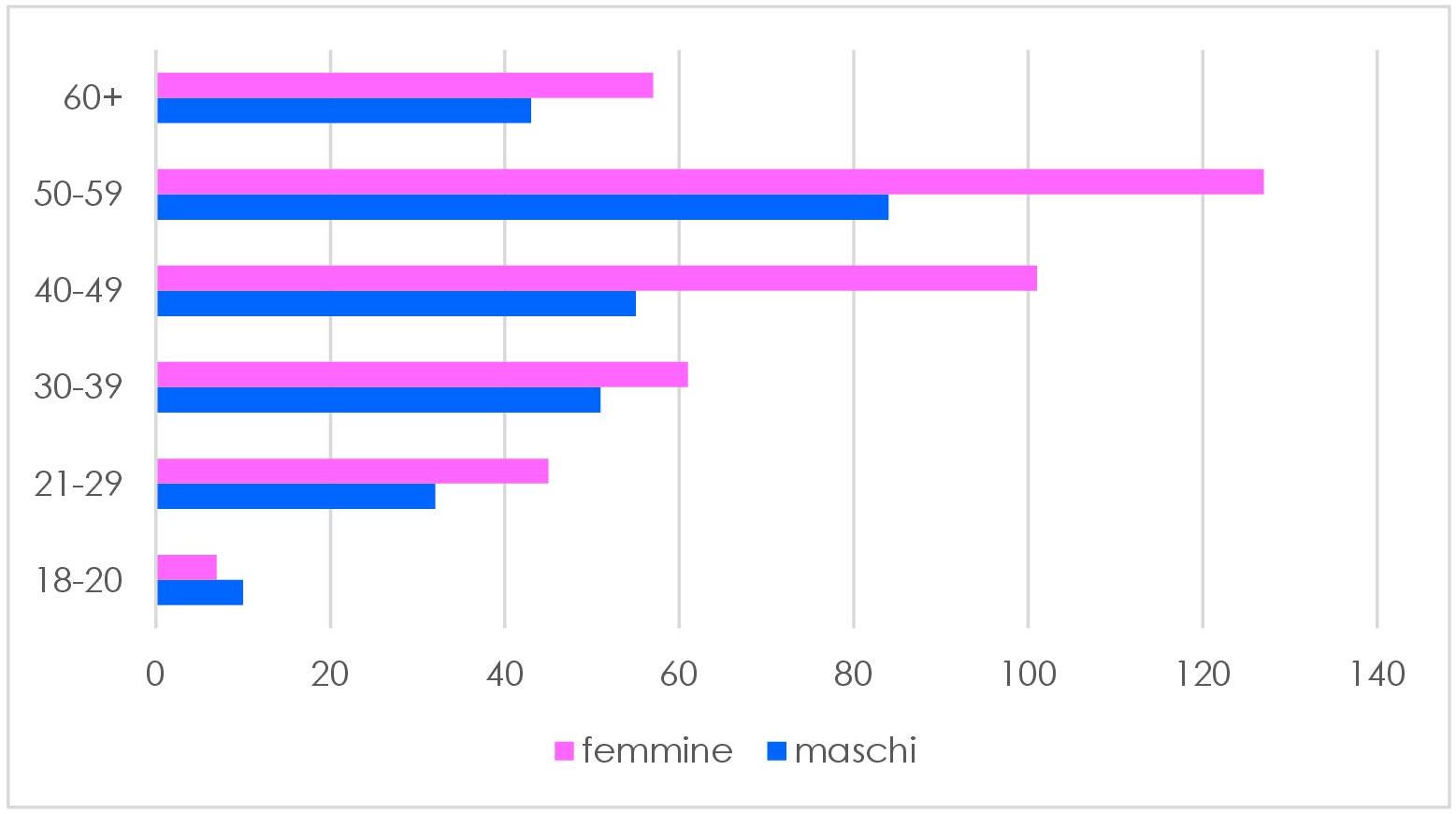
È importante riconoscere che la fascia di età 18-20 è la meno significativa, visto che hanno partecipato solo 18 persone (meno del 3%). Inoltre, visto che, per la maggior parte, i partecipanti sono ancora impegnati nella formazione, abbiamo deciso di non inserire i loro dati nei grafici successivi. La fascia più nutrita è quella dell’età compresa tra i 50 e i 59 anni (31%), nella quale è presente ancora una maggioranza femminile (127 risposte contro 84). La seconda fascia più numerosa è quella 40-49 (23%), mentre le altre tre fasce, oltre ad essere equamente distribuite per genere, hanno raccolto più o meno lo stesso numero di risposte.
Per verificare quanto il campione fosse poco rappresentativo della popolazione italiana, almeno in termini di età, abbiamo confrontato i dati dei nostri intervistati con quelli riferiti alla popolazione residente al 1° gennaio in Italia[2].
Soffermandoci anche solo sulla percentuale dei maschi e delle femmine,
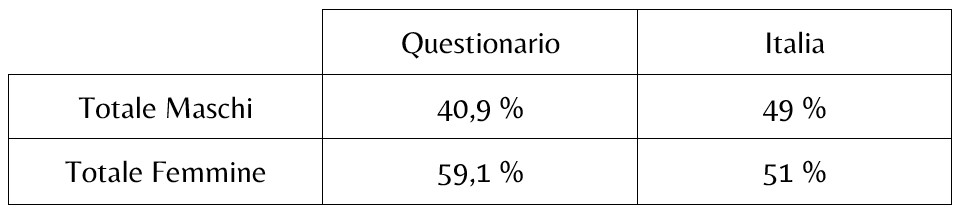
possiamo notare come la suddivisione per genere del nostro questionario non rispetti la suddivisione della popolazione italiana, dai 18 agli 85 anni.
Se allarghiamo lo sguardo e consideriamo la suddivisione per età, vediamo parecchie incongruenze, ma prima è necessario precisare che la fascia di età più alta non era stata da noi definita, indicandola semplicemente come “60 e più”. Ripensando al campione intervistato, al fatto cioè che l’età più alta è quella dei nostri nonni e che oltre una certa età è più raro che accedano ai social (e quindi al questionario), abbiamo considerato come tetto gli 85 anni.
Già solo la suddivisione per età, quindi, ci restituisce il profilo di un campione che non può essere considerato rappresentativo della popolazione italiana.
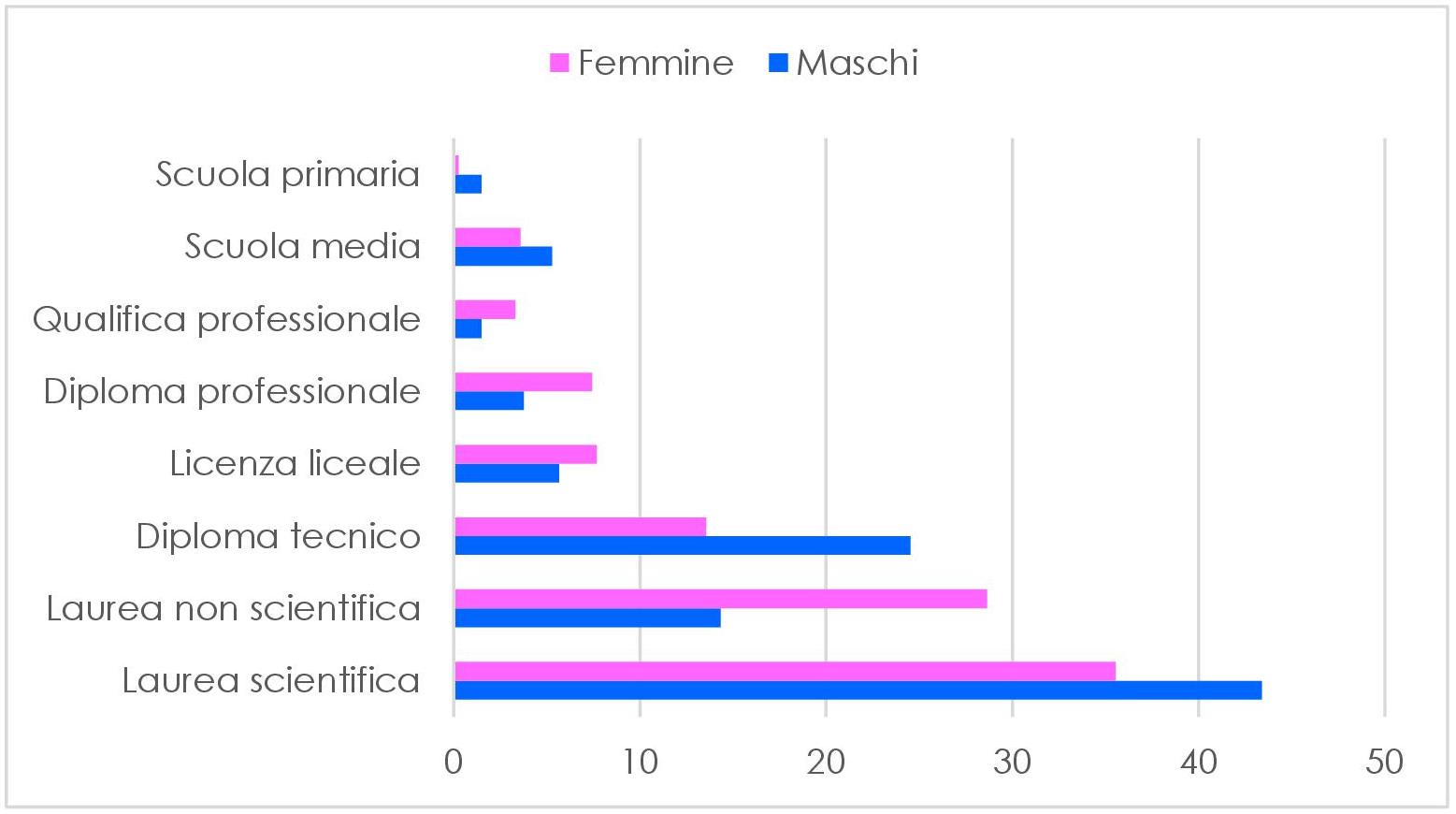
TITOLO DI STUDIO:
Dai grafici suddivisi per titolo di studio, possiamo notare una netta superiorità dei laureati, seguiti dai diplomati in materie tecniche. Possiamo notare che il numero delle licenze liceali è inferiore al numero dei diplomi tecnici, ma questo può essere dovuto al fatto che, mediamente, chi sceglie di frequentare un liceo prosegue con gli studi universitari, mentre è più probabile che un diplomato all’istituto tecnico chiuda il proprio percorso di studi dopo il diploma. Pochi sono i votanti che hanno interrotto il proprio percorso scolastico prima della scuola secondaria di secondo grado e, in genere, hanno superato i 60 anni di età, ma questo può essere dovuto al diverso obbligo scolastico: sebbene dal 1948 fosse stato imposto un ciclo di istruzione della durata di minimo otto anni, spesso la maggior parte dei bambini finiva solo la scuola primaria, nonostante le medie fossero obbligatorie. Si iniziò a frequentare obbligatoriamente la scuola media solo dal 1963, cioè per la fascia d’età che oggi è al di sotto dei 70 anni. Man mano che ci si avvicina alle fasce d’età più giovani, il grado di istruzione si innalza, grazie all’obbligo scolastico portato a 16 anni nel 2006[3]. È aumentato, inoltre, il numero di laureati, a seguito del decreto del 1999 con il quale vennero riformati i corsi di studio universitari, creando la laurea triennale e quella specialistica, e alcune professioni hanno visto un cambio di titolo di studio, basti pensare alla formazione infermieristica che, fino al 1995, è avvenuta nelle scuole regionali ed è diventato successivamente universitaria.
Quanto detto non vede differenze sostanziali nei generi, anche se i diplomi risultano essere distribuiti in maniera più omogenea tra le donne, e per gli uomini si tratta soprattutto di diplomi tecnici.
Infine, per ogni titolo di studio, abbiamo calcolato la percentuale di distribuzione in base al genere e abbiamo rilevato che:
- La scuola primaria, la scuola media, il diploma tecnico e le lauree scientifiche vedono una maggioranza maschile
- I restanti livelli di istruzione vedono una maggioranza femminile
Sembra quasi che l’ambito scientifico e tecnico siano un dominio maschile, stando al nostro campione!
[1] Bergamini, Barozzi, Trifone, Algebra.blu 1 con Statistica, Zanichelli, ISBN 9788808998828, capitolo a Introduzione alla statistica, p.a3
[2] http://dati.istat.it/Index.aspx?QueryId=42869#
[3] https://it.wikipedia.org/wiki/Storia_dell%27istruzione_in_Italia#La_scuola_nell'Italia_repubblicana
Prosegui con Matematica e mondo del lavoro
© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy





