Visualizza articoli per tag: tassellazioni

Alla ricerca di ispirazione per il Carnevale della Matematica, con il tema “matematica estiva” lanciato da Maurizio Codogno, faccio scorrere le foto della scorsa estate e realizzo che le foto di prati verdi e boschi rigogliosi che costellano in genere le mie estati (sono un’appassionata di camminate in montagna) si alternano a foto di bottiglie di Klein colorate realizzate all’uncinetto, di pantaloni molto ampi e altre amenità legate alla topologia. Dal 2016 ad oggi, le mie estati sono state arricchite dalla preparazione dei laboratori per il Festival di BergamoScienza, che si tiene ad ottobre, e, quindi, so che anche quest’anno la mia matematica estiva sarà ricca di prospettiva, visto che il mio cellulare già esplode di fotografie inerenti disegni prospettici, illusioni ottiche, anamorfosi, carte geografiche e tanto altro.

Vorrei concentrarmi, però, in questo caso, sulla matematica in montagna: il mio occhio ormai allenato (ossessionato, direbbe qualcuno) è abituato a individuare la matematica ovunque, e, mentre sono impegnata a raggiungere la meta del giorno, la mente vaga e cerca la matematica nella natura.

Comincio con gli straordinari giochi di luce che sul finire dell’estate interessano le due montagne (sacre, per gli antichi Camuni) che si fronteggiano nella Media Valle Camonica, il Pizzo Badile, protagonista al mattino, e la Concarena, che si ammanta di luce al tramonto. I raggi di luce, che all’Equinozio proiettano l’ombra delle montagne nel cielo, si mostrano come semirette con un’origine comune.

Quando si cammina in montagna, uno dei problemi con i quali ci si confronta di più è quello della pendenza: sono in bilico tra una terza e una quarta liceo scientifico e realizzo che quella che abbiamo visto fino a questo momento come pendenza della retta (ed esplorato in lungo e in largo anche con la cinematica e i diagrammi dei moti unidimensionali), ora diventerà la tangente dell’angolo formato dalla retta con l’asse delle ascisse, visto che cominceremo ad aggirarci tra i meandri della goniometria. La pendenza ha un ruolo determinante nella scelta di una camminata in montagna, perché non conta solo il dislivello che si deve colmare per raggiungere la meta, ma anche lo sviluppo del percorso. Diciamo che la pendenza è forse l’aspetto matematico più bistrattato durante le camminate di gruppo: il tratto che per chi ha allenamento e abitudine alla fatica è in genere un falso-piano, per chi è affaticato diventa una salita ripidissima.

«… chi va in montagna mi capisce al volo: una di quelle volte che ti sei alzato la mattina presto, stai sudando ormai da ore come un becco, sotto lo zaino, verso il rifugio che è là… son tre ore che è là… perché li spostano! Ci ho messo anni a capirlo: lo fanno per il tuo bene ma li spostano, chiaro!» [dal monologo teatrale di Marco Paolini Il racconto del Vajont]

Camminare in montagna aiuta a mettere le cose in prospettiva, per questo l’attività ha degli innegabili benefici psicologici, ma fa anche vedere le cose da un’altra prospettiva: «Tu sei là che ti domandi chi è che te l’ha fatta fare tutta ‘sta fatica, ti casca l’occhio indietro un attimo, e capisci da solo che valeva la pena di fare tutta la fatica del mondo per arrivare là, in quel momento li, perché giù, il fondo valle da dove sei partito, è già coperto di nuvole, ma tu ormai sei sopra. È limpido sopra. A trecentosessanta gradi hai le montagne, le crode, (…) che ti par di poterci volar sopra come un rapace» [Marco Paolini] Infine, la prospettiva cambia la nostra percezione delle altezze:

La seconda foto è stata scattata dal fondo valle, mentre la prima è stata scattata dal Bivacco Adamone, che si trova a un’altitudine di 1456 m. La percezione che si ha dal fondo valle delle altitudini è ben diversa dalla realtà: il Pizzo Badile ha un’altitudine di 2435 m, mentre la conca del Tredenus che lo circonda possiede parecchie cime, tutte più alte, ad esempio: Cima del Dosso (2785 m), Cima Meridionale (2796 m), Corno delle Pile (2805 m). Ecco spiegati gli inganni della prospettiva e, forse, anche il motivo per cui tendiamo a stimare la meta più vicina di quanto non sia.

Lungo il cammino, fra la vegetazione possiamo riconoscere delle felci: costituiscono un ottimo esempio di frattali, dei quali prima di BergamoScienza 2018 e della costruzione del grande triangolo di Sierpinski avevo un’idea molto vaga. Secondo la definizione di Wikipedia, «un frattale è un oggetto geometrico dotato di omotetia interna: si ripete nella sua forma allo stesso modo su scale diverse, e dunque ingrandendo una qualunque sua parte si ottiene una figura simile all’originale». Infatti, anche se concentriamo la nostra attenzione su un piccolo rametto di felce, questo potrebbe essere, nella giusta scala, la felce più grande dalla quale è stato preso.

Se abbiamo la fortuna di andare in montagna dopo una nottata di pioggia, oltre a poter apprezzare maggiormente il panorama, che è più limpido, potremmo anche imbatterci in una lumaca che attraversa il sentiero. Ma la spirale sul suo guscio è logaritmica o archimedea? La spirale archimedea mantiene costante la distanza tra due spire successive, mentre per la logaritmica questa distanza cresce secondo una progressione geometrica. Mi sono portata a casa la domanda e ho cercato, nei giorni successivi, una risposta. L’ho trovata nel blog Base 5 di Gianfranco Bo, il quale ipotizza anche una risposta sul motivo per cui la spirale della chiocciola sia logaritmica: la chiave potrebbe essere nella necessità del mantenimento della forma durante la crescita, ma per un approfondimento non resta che dare un’occhiata al suo lavoro.

Ritroviamo il lavoro di Gianfranco Bo anche nel post I fiori di Fibonacci del blog Sanoma. In effetti, ammirare i fiori, in montagna o altrove, rimanda sempre alla successione di Fibonacci, la sequenza di numeri che comincia con la coppia di 1 e prosegue autogenerandosi: il terzo numero è la somma dei primi due (2) e così ogni numero è la somma dei due che lo precedono, facendoci ottenere 1 1 2 3 5 8 13 21 34 55 89… Nel mio collage di foto compare del Semprevivo dei tetti, esempio matematico classico come possiamo vedere in questa mostra fotografica organizzata dall’Università di Pisa, il fiore del Ginepro, la minuartia austriaca, per me ottimo esempio di pentagono regolare, la genzianella primaverile, che spicca per il suo colore, la primula comune, che possiamo trovare anche senza bisogno di salire ad alta quota, il papavero alpino retico, la macchia di colore che spunta tra le rocce, e infine la mitica stella alpina.

Se durante la camminata raggiungiamo un laghetto, come nel caso del Lago Smeraldo in Val di Non o del lago d’Aviolo in Valle Camonica, si può osservare la simmetria assiale all’opera. La bellezza, in questo caso, è duplicata, grazie all’armonia delle forme e ai colori, che ci restituiscono il sapore di un lago incontaminato.

Anche i corsi d’acqua regalano grandi soddisfazioni matematiche: ogni volta che mi affaccio sulla Valle Adamé e vedo il serpeggiare del torrente Poia, che di anno in anno scava sempre di più il suo percorso creando nuove anse, non posso che ricordare la presenza nascosta del pi greco. Il matematico Hans-Henrik Stolum, in un lavoro pubblicato su Science nel 1996, ha mostrato che se si divide la lunghezza effettiva di un fiume, dalla sorgente alla foce, per la sua lunghezza in linea d’aria, si ottiene, approssimativamente, pi greco. Sul sito Matematica Russell, curato dal dipartimento di matematica e fisica dell’omonimo liceo di Roma in collaborazione con gli studenti, troviamo una precisazione: «Questo rapporto, però, non è una legge, infatti il rapporto di pi greco si trova più comunemente in quei fiumi che scorrono attraverso pianure che hanno un dislivello molto tenue.» Il torrente Poia ha, appunto, le caratteristiche necessarie.

Il penultimo tassello di questa camminata in montagna rimanda alle tassellazioni (che per quanto mi riguarda assocerò sempre alla prima esperienza con i laboratori di BergamoScienza): questo ultimo tratto del sentiero che porta al Lago della Vacca, realizzato con il granito dell’Adamello, ricorda in qualche modo una tassellazione. È un tratto pianeggiante, durante il quale si può ammirare il panorama, senza essere sovrastati dalla fatica.

L’ultimo passo, però, è quello più goloso: ormai raggiunta la meta, si può accedere al Rifugio, per riposare, riscaldarsi con un bel tè caldo e mangiare una fetta di torta. La mente, ormai allenata a trovare la matematica ovunque, non può che ritrovare la scodella di Galileo tra le tipiche scodelle dei rifugi, e chiedere di avere un settore circolare abbastanza ampio, quando sceglie la torta che preferisce.

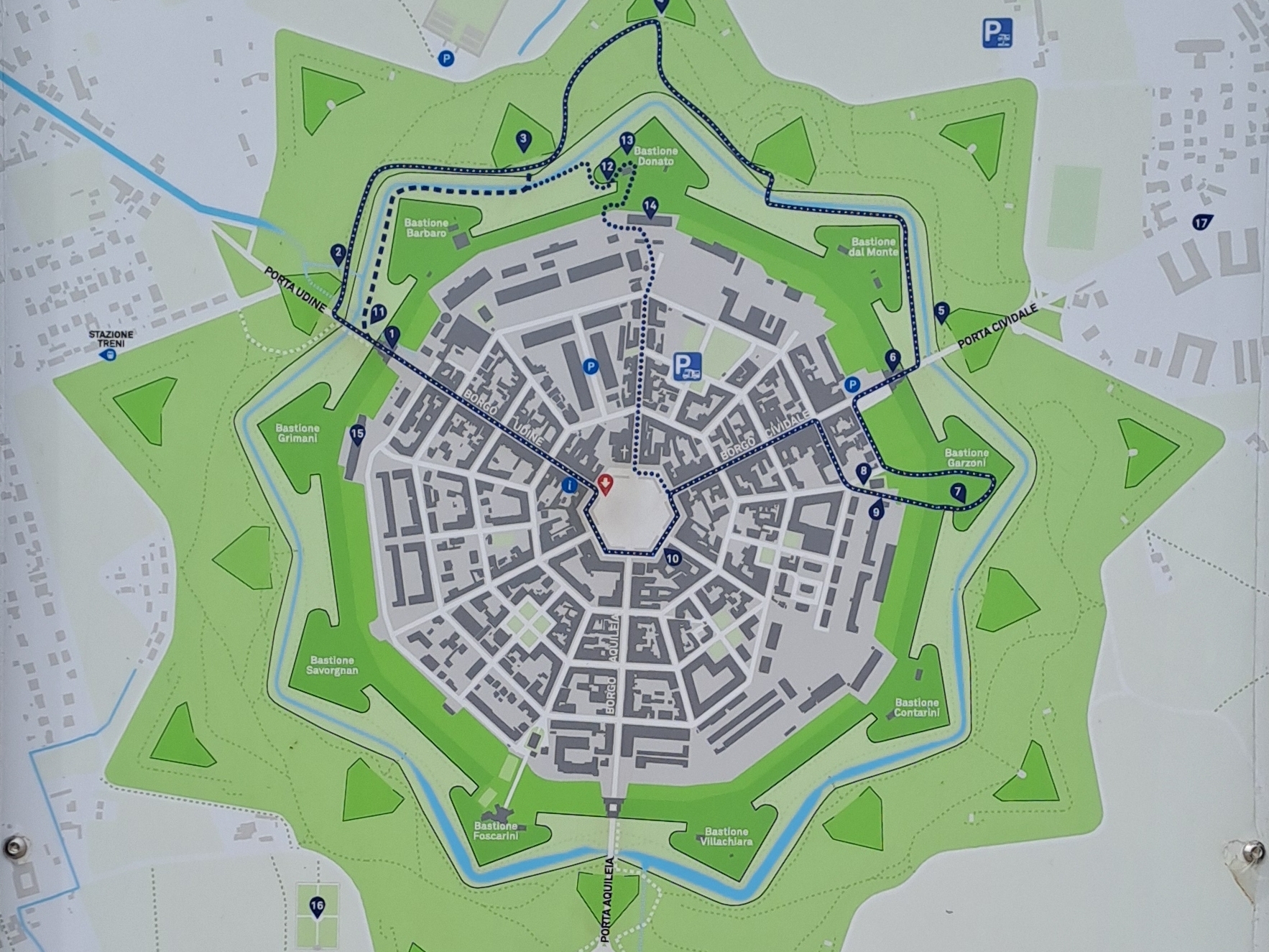
Mi piace organizzare viaggi per le mie classi, perché mi piace mostrare la matematica attorno a noi, nella realtà. Quando scelgo una meta, comincio, quindi, dalla matematica o dalla fisica, perché visitando una città si è immersi, consapevolmente, nell’arte e nella storia, ma si dimentica la componente scientifica, meno visibile, o forse visibile solo per gli occhi più allenati. L’ultima scelta è stata Trieste, ma, durante il viaggio di andata, abbiamo scelto di fermarci prima a Palmanova, la città-fortezza, con la sua stella a nove punte e il suo lato di 400 m che garantiva la possibilità per i cannoni della città di gestire la difesa, mentre il muro inclinato smorzava la potenza dei cannoni nemici, come è stato spiegato nel video di Geopop. Le strutture difensive della città ci hanno regalato degli scorci piacevoli, visto il cielo sereno, che mostrava un bel contrasto con il verde della vegetazione primaverile.

Al centro della città c’è una piazza esagonale, centro proprio della ragnatela, costituita dalle vie che partono a raggio e che si sviluppano in poligoni regolari concentrici. Nelle mura si aprono tre porte e le strade che passano attraverso esse si incontrano nel centro della piazza formando angoli di 120°, in una manifestazione di simmetria che diventa bellezza.

La seconda sosta è stata il Santuario Mariano del Monte Grisa, che domina la città di Trieste e permette, quindi, di vedere la città dall’alto, in un assaggio di ciò che ci aspetta. La struttura in cemento armato è tipica dell’architettura brutalista, che si è sviluppata in Inghilterra negli anni Cinquanta del secolo scorso. Il triangolo è la struttura modulare che si ripete sempre uguale, ma è un triangolo isoscele particolare, con la base uguale all’altezza, ovvero inscrivibile in un quadrato e con un lato obliquo che ha misura pari a metà del lato moltiplicato per radice di 5. Il triangolo ha una forte valenza simbolica per la fede cristiana, richiamando la trascendenza e la Trinità, ma in questo caso va oltre, ricordando la struttura di un alveare e proponendo una A, facilmente visibile, e una M (che ho faticato a far cogliere ai miei alunni), che sono le iniziali di Ave Maria, la celebre preghiera cattolica.

All’interno del Santuario ci sono due chiese, una sopra l’altra e passare da quella superiore a quella inferiore fa sentire schiacciati: come quella superiore fa sentire lo slancio verso l’alto, quella inferiore fa sentire il peso della gravità, e realizza l’intento dell’ingegnere Antonio Guacci, visto che sembra davvero di trovarsi nella stiva di una nave.

Giunti in città, nonostante il maltempo, abbiamo fatto un breve percorso per entrare in contatto con l’anima letteraria della città, quella più nota, quella presente negli antichi caffè letterari e nelle statue di Joyce, Saba, D’Annunzio e Svevo. Visto che il nostro albergo era nel quartiere teresiano, la nostra prima tappa è stato il Canal Grande, dove abbiamo incontrato James Joyce. Su questo canale si affacciano il Tempio Serbo-Ortodosso di San Spiridione e la Chiesa di Sant’Antonio Nuovo, come esempio dell’anima poliedrica della città, che non è solo il punto di incontro di tradizioni diverse - la Slovenia, l’Italia e l’Austria - ma è anche l’incrocio di religioni diverse. Il passo successivo è stato la statua di Umberto Saba, in via Dante Alighieri: il povero poeta è stato privato della pipa, spesso rubata, ma anche del bastone, ma è stato facile immaginarlo percorrere le strade cittadine mentre si dirigeva verso la sua libreria, esempio di ciò che hanno vissuto gli ebrei con le leggi razziali.

Inoltrarsi nella città ha significato anche raggiunge la sua anima più antica, con il Teatro romano, che con la sua apertura semicircolare e i suoi gradoni non può che richiamare la matematica! Piazza della Borsa, il “secondo salotto buono cittadino”, ci ha accolto con la sua eleganza (anche se a me il timpano con l’orologio del Palazzo della camera di commercio ha ricordato l’orologio di Hill Valley in Ritorno al Futuro) e Gabriele D’Annunzio non poteva che starsene elegantemente seduto su una panchina (questa statua è stata ribattezzata la “statua della discordia”). L’ultimo luogo della giornata è stato Piazza Unità d’Italia, con la sua Fontana dei quattro continenti sormontata dalla statua alata che rappresenta la città di Trieste. La Fontana è un simbolo della rinascita della città, visto che era stata spostata per consentire il discorso del Duce, che annunciava la promulgazione delle leggi razziali, ed è stata rimessa al suo posto solo in tempi recenti: è stato facile farsi portare indietro nel tempo, pur cercando di sostituire quel ricordo amaro con quello del presidente Luigi Einaudi, che il 4 novembre del 1954, insieme al sindaco della città, ha aperto i festeggiamenti per il ritorno di Trieste all’Italia.

Il suo ritorno alla normalità in tempi così recenti ha ricordato a tutti che Trieste è la città che è solo da poco tempo e che le ferite che ha subito durante la Seconda guerra mondiale forse non sono ancora del tutto rimarginate. La sosta al Santuario Mariano ci aveva permesso di cogliere questa sofferenza, perché non è possibile visitare il santuario senza ricordarne la nascita, con la risposta di Mons. Santin allo Stato maggiore tedesco: «Si stanno avvicinando da due parti gli eserciti. Resistere per farsi ammazzare e per distruggere Trieste? Questa città è la porta d’Europa centrale; perché distruggerla senza alcun scopo? Non è una città germanica; voi, tedeschi, pensate a difendere quelle. Questa è una città italiana, e gli italiani non avrebbero mai dimenticato.» (27 aprile 1945) Dopo aver individuato tutti i palazzi che si affacciano sulla Piazza, dopo aver raccontato della torre campanaria e dei due mori Micheze e Jacheze, e averli sentiti scandire il trascorrere del tempo, abbiamo volto lo sguardo al mare, il quarto lato della piazza, a significare l’apertura della città al mondo.

L’Immaginario Scientifico è stato il punto focale del secondo giorno di visita, visto che l’intero viaggio è stato costruito attorno alla disponibilità del museo: la visita è andata ben oltre le aspettative di noi insegnanti, visto che al termine della mattinata è stato difficile allontanare i ragazzi, che si sono mostrati coinvolti e incuriositi, entusiasti delle attività, delusi da quella che è sembrata una permanenza troppo breve. Durante la visita, abbiamo affrontato il percorso sull’energia con un laboratorio che ha permesso di focalizzare l’attenzione sulle energie rinnovabili, realizzando l’elettrolisi e studiando il funzionamento dei pannelli fotovoltaici, variandone l’inclinazione e la distanza rispetto alla fonte di luce e calore, e attraverso l’inserimento di filtri colorati.

La seconda parte del percorso ha visto come protagonisti i vari exhibit che hanno permesso ai ragazzi di toccare con mano la scienza, di sperimentarla in prima persona, esplorando e divertendosi. La prima parte del percorso ha permesso a tutti di cogliere la centralità della scienza nella città di Trieste, a partire dalla figura di Paolo Budinich, che insieme ad Abdus Salam, fondò a Trieste il Centro internazionale di fisica teorica. Con la prima mappa, topologica, i ragazzi hanno potuto vedere i collegamenti tra i vari scienziati, il loro ruolo nel Sistema Trieste, la presenza di un esiguo numero di donne, ma l’importanza della ricerca scientifica in questa città, visto che se la media in Italia è di 5 ricercatori ogni 1000 persone, a Trieste è di 37. Il piano superiore della struttura ha permesso di esplorare la matematica con il gioco: tassellazioni e puzzle, serie di Fibonacci, cubi di binomi e quadrati di trinomi, simmetrie con la simpatica scrittura allo specchio, la camera oscura, le illusioni ottiche… insomma, così tanta matematica da lasciare inebriati!

La meta successiva, nel pomeriggio, è stata la Grotta Gigante: la grotta non è solo magnificenza e bellezza indescrivibile, ma anche laboratorio scientifico, come ci ricordano i due pendoli centrali, usati per le rilevazioni sismiche.

La giornata si è conclusa con un ulteriore giro in città: ci siamo fatti lasciare alla Cattedrale di San Giusto, in cui il rosone centrale ha rimandato alla matematica (ovviamente!), ma ha anche evidenziato la mancanza di simmetria della struttura. Una mancanza presente anche all’interno, visto che le colonne che separano le navate sono spaziate in modo diverso ai due lati dell’altare. I ragazzi hanno notato questa rottura della simmetria, evidenziandola come mancanza di bellezza!

Dopo la salita al castello per vedere da vicino i due automi originali, Micheze e Jacheze,

siamo ridiscesi lungo la strada antistante la cattedrale, verificando la distanza in passi dall’Arco di Riccardo. Ci siamo soffermati sul nome dell’arco, ma la mancanza di simmetria (successiva alla sua costruzione) è stata poco notata: i ragazzi cominciavano a scalpitare, assaporando il momento di libertà che abbiamo concesso loro dopo aver raggiunto l’inetto triestino, Italo Svevo.

L’ultimo giorno di visita è stato un’oscillazione tra presente e passato, avendo scelto di lasciare ampio spazio ad entrambe le anime della città: abbiamo visitato l’Area Science Park di Padriciano, all’origine un campo profughi, dove i ricercatori Alessandro e Pietro, insieme allo studente della magistrale di fisica Nicolò, ci hanno guidato alla scoperta dei lavori che vengono svolti all’interno dei laboratori dell’INFN. Dopo averci parlato della fisica delle particelle e averci tratteggiato il quadro storico, estendendo il discorso fino al CERN, hanno permesso ai nostri studenti di capire cosa significhi studiare le particelle, anche attraverso il confronto tra le strumentazioni in uso nel passato e quelle più moderne. In una sala riunioni, gli studenti hanno poi potuto fare domande, in un piccolo percorso di orientamento.

La seconda parte della mattinata ha avuto per protagonista il Monumento Nazionale delle Foibe di Basovizza. Lo storico che ci ha accompagnato in questo percorso ha fatto in modo che potessimo cogliere nei particolari la storia più recente della città, a partire dalla fine della Prima guerra mondiale fino ai giorni nostri. Il passato delle foibe è un passato che è ancora presente, se pensiamo anche solo a quanto ci ha raccontato lo storico della sua esperienza: quando fa la guida a Basovizza viene etichettato come fascista e quando si ritrova a fare la guida alla Risiera di San Sabba viene etichettato come comunista. La riflessione che è stata sollecitata è andata ben oltre i luoghi visitati e il tempo studiato, mentre il monumento, con le sue linee scarne ed essenziali, ha richiamato le macchine della fisica che avevamo visto in piazza a Palmanova: in quel caso erano servite per costruire le fortificazioni della città, in questo sono state utilizzate per calarsi all’interno della foiba a carpirne i segreti. Questa comunicazione tra interno della foiba e mondo esterno è stata bloccata da un coperchio che, con la sua fissità e la ruggine, dà l’idea di un evento fermo nel tempo, lontano ma al tempo stesso vicino.

La visita alla città di Trieste ci ha permesso di notare come il linguaggio della matematica, astratto e simbolico, possa essere lo strumento ideale per comunicare attraverso i simboli, basti pensare al Santuario Mariano del monte Grisa. Il rigore della matematica, inoltre, può diventare espressione di regolarità e bellezza, presente in Piazza Unità d'Italia, è stata manifestazione di eleganza e maestosità, mentre la sua assenza, come nella Cattedrale di San Giusto, ha segnalato una mancanza di armonia. Mi ha colpito il fatto che Trieste sia nominata soprattutto come città letteraria, mentre la sua essenza è, ancora una volta, più articolata e poliedrica di quanto sia possibile cogliere con un primo sguardo: Trieste è una città scientifica, e spesso il turista medio coglie “solo” la bellezza artistica, senza rendersi conto che l’arte sceglie la matematica per enfatizzare certi aspetti. Federica Manzon, nella guida di Trieste del Touring Club, scrive: «A scuola ci insegnavano le poesie di Rilke che a Duino inseguiva l’Angelo del Tempo, poi Svevo ovviamente e ci portavano in visita alla libreria antiquaria del poeta [Saba]. Nei caffè non mancavano mai le presentazioni di qualche autore cittadino, meglio se poco noto nella nazione. Così una generazione dopo l’altra è cresciuta nel culto della città di carta e la letteratura è considerata patrimonio del Dna triestino: un mito tutto rivolto al passato, un culto dei morti poco celebrati in vita. Passa invece del tutto sotto silenzio la presenza in città di uno degli avamposti scientifici più importanti al mondo.» Così Trieste, connubio di tradizioni (Slovenia, Austria, Italia), incontro di religioni, diventa anche culla delle “due culture”, l’anima umanistica e quella scientifica, che ognuno di noi porta dentro di sé, ne sia consapevole oppure no.

Durante la costruzione del percorso di visita ho letto dell’impegno di Abdus Salam, quello che Pietro Greco definisce il pakistano visionario, che «propose di allestire un centro dove formare alla fisica teorica i giovani più valenti dei paesi in via di sviluppo. Non solo per il valore culturale intrinseco di una simile iniziativa, ma anche perché la scienza è il motore dello sviluppo economico. E la scienza di base è il primum movens della scienza. In altri termini – questo era il pensiero di Abdus Salam, in controtendenza rispetto a molto analisti – i paesi in via di sviluppo non possono fare a meno di eccellere anche nelle scienze più astratte se vogliono recuperare il gap economico che li separa dai paesi più avanzati.». Ci è stato fatto notare come l’eccellenza di Trieste sia diversa dall’eccellenza americana: per accedere alle grandi università statunitensi, devi dimostrare di essere all’altezza, mentre Trieste apre le proprie porte a chi questo sapere lo vuole costruire, per portarlo poi nel proprio paese di origine, per permettere anche ai paesi meno fortunati di costruirsi un futuro.

Fotografie realizzate durante il viaggio di istruzione a Trieste, il 17, 18 e 19 aprile 2024, con le classi 3AS e 3ES.