Sistemi lineari novembre 2023 - 2
Verifica di matematica, classe seconda liceo scientifico.
Argomento: sistemi lineari e geometria euclidea. Verifica di recupero per assenti.
Durata: 70 minuti.
Sistemi lineari novembre 2023
Verifica di matematica, classe seconda liceo scientifico.
Argomento: sistemi lineari e geometria euclidea.
Durata: 110 minuti.
Sbagliando si impara
«Sbagliando si impara. Storie di geni che non si sono arresi» è stato pubblicato dalla casa editrice White Star nel 2022 nella collana National Geographic Kids. Gli autori sono Max Temporelli e Barbara Gozzi: Temporelli è fisico divulgatore, dal 2017 è autore e voce del celebre podcast F***ing Genius, è autore del libro «F***ing Genius» per HarperCollins Italia (2020), di «Innovatori» per Hoepli (2015) e di «Noi siamo tecnologia» per Mondadori (2021), a dimostrazione del fatto che il tema dei geni e delle invenzioni è proprio nei suoi geni. Barbara Gozzi è socia dell’agenzia di storytelling Book on a Tree, senior editor, ghostwriter e autrice di «La maledizione di Bloody Mary» con Fabbri (2021). Le illustrazioni sono di Agnese Innocente, vincitrice del Premio Andersen per il miglior libro a fumetti del 2021, con il libro «Girotondo», scritto con Sergio Rossi.
Il titolo e il sottotitolo ci raccontano già molto del contenuto del libro, svelandoci il valore pedagogico dell’errore e l’importanza di non arrendersi. I protagonisti sono dieci inventori, alcuni meno noti di altri, ma riconoscibili grazie alla celebrità delle loro invenzioni. La rassegna comincia con Thomas Alva Edison e la lampadina, si procede con Jan Ernst Mazeliger, che ha permesso di realizzare calzature in modo industriale, Guglielmo Marconi e le telecomunicazioni, Wilson Greatbatch con il pacemaker, James Dyson con l’omonimo aspirapolvere, Margarete Steiff e l’orsetto Teddy, Stephanie Louise Kwolek inventrice del kevlar, Charles Goodyear con il procedimento della vulcanizzazione, Percy Spencer con il microonde e John Stith Pemberton con la famosissima Coca Cola. Questi otto uomini e due donne hanno realizzato qualcosa di unico, che ha lasciato un segno, ma le loro storie sono costellate di errori: ci imbattiamo subito nei 1999 modi di non fare una lampadina scovati da Edison, che viene però presto superato dai 5126 prototipi di James Dyson, che ha speso 15 anni per realizzare un aspirapolvere. Questo perseverare per sostenere un’intuizione, nonostante gli errori, può portare lontano, può aprire nuove strade, può portare a risultati diversi da quelli che ci si aspettava, come la Coca Cola, la vulcanizzazione e il kevlar, nati da errori casuali. Ma non sarebbe possibile ottenere un risultato, se non ci fossero la passione e la determinazione, ingredienti fondamentali per reggere 15 anni di tentativi. I dieci geni ci dimostrano che per arrivare al successo è necessario andare controcorrente, allenarsi a combattere lo status quo, non ascoltare chi dice che è inutile ciò che stiamo facendo.
Dopo una breve pagina introduttiva di carattere biografico, le invenzioni vengono presentate attraverso un paio di tavole di fumetti, per poi affrontare i dettagli dell’invenzione in un altro paio di pagine, dove campeggia una citazione del genio o un commento al suo lavoro. La conclusione, in poche righe di stampatello maiuscolo, sottolinea quale sia stata la rilevanza dell’errore in quella storia particolare. Le illustrazioni sono una parte centrale del libro: aiutano anche i più piccoli (il libro è pensato per bambini dagli 8 anni) a visualizzare le invenzioni, e l’approccio, pur semplificando i contenuti, permette di cogliere pienamente l’unicità e la straordinarietà di questi dieci “geni che non si sono arresi”.
Doctor Newtron
«Doctor Newtron, la scienza nel fumetto» è una recentissima pubblicazione di Feltrinelli Comics. L’autore è Dario Bressanini: docente di chimica presso l’Università degli Studi dell’Insubria a Como, noto divulgatore scientifico, conosciuto come “l’amichevole chimico di quartiere”, ha scritto numerosi libri di carattere divulgativo a partire dal 2009, come «OGM tra leggende e realtà» (2009) e «Le bugie nel carrello» (2013), dedicati alla disinformazione alimentare, «La scienza della pasticceria» (2014), «La scienza della carne» (2016), «La scienza delle verdure» (2019), «La scienza delle pulizie» (2022) e l’ultimissimo «Fa bene o fa male?» (2023). Ha scritto anche «Contro natura», in collaborazione con Beatrice Mautino, (2015) e un libro di matematica con Toni Toniato, «I giochi matematici di fra’ Luca Pacioli» (2011).
«Doctor Newtron» è a metà tra una graphic novel e un saggio scientifico: «Questo libro […] mostra come la scienza nel mondo reale si è intersecata con il mondo dei fumetti dei supereroi, come l’ha influenzato, come è cambiata la rappresentazione della scienza e degli scienziati nell’universo delle nuvolette.» Da un lato gli eventi della vita reale determinano un aumento della presenza della scienza tra le pagine dei fumetti, dall’altro, l’aumentata esposizione dei ragazzi alla scienza attraverso i fumetti potrebbe aver «giocato un ruolo importante nell’immaginario di tutti quei bambini e quelle bambine che sono stati ammaliati da eroi ed eroine in calzamaglia colorata». Dario Bressanini si dice «abbastanza convinto» che una parte dei dottorati in più nelle materie scientifiche sia dipesa dall’aumentato interesse dei fumetti nei confronti della scienza. Una sorta di circolo virtuoso, nel quale lo stesso autore è rimasto coinvolto. Coniugando, quindi, le due passioni, Bressanini ripercorre la storia della scienza attraverso le vicende di Tom Ernea Taylor, meglio noto come il supereroe Doctor Newtron: Taylor è praticamente l’alter ego dell’autore, perché oltre a rivivere in parte la sua vita, ha un superpotere chimico, visto che può trasformare gli elementi (un alchimista moderno!) ed è la guida di questo viaggio, «come Dante con Virgilio». «Se è vero che, tranne il Dottor Newtron, nessun supereroe della Golden Age era uno scienziato», è ancora più vero che nessun supereroe della Golden Age è stato ideato da un chimico. Nel compiere questa impresa (unica nel suo genere!), Bressanini è stato aiutato e spinto dal fumettista Tito Faraci: «con non pochi timori e pieno di soggezione, ho iniziato la stesura dei soggetti, sempre sotto lo sguardo attento di Tito.» Nel testo ritroviamo, principalmente, le illustrazioni di Luca Bertelè, ma ci sono anche Biagio Leone, Giuseppe Gho e Maurizio Rosenzweig.
Le prime parole dell’introduzione, oltre ad avere un sapore autobiografico, contengono il resto del libro: «In molte vicende c’è un prima e c’è un dopo, e un evento epocale preciso e facilmente individuabile a fare da spartiacque». Le storie del Dottor Newtron sono la chiave di volta per focalizzare l’attenzione su questi singoli eventi, che hanno cambiato il corso della storia, sia quella reale che quelle dei fumetti. Il primo evento è l’esplosione della bomba atomica, che «cambiò drasticamente le sorti della Seconda guerra mondiale, ma anche la percezione che la società aveva della scienza e degli scienziati», dato che dall’immagine di scienziato svagato, con le boccacce di Einstein, si è passati a scienziati più realistici e reali, come Robert Oppenheimer, con una scienza che da «ricerca intellettuale» con un valore astratto, diventa qualcosa che «fornisce meraviglie, conoscenza, cultura, ma anche supremazia militare, tecnologica ed economica.». Il secondo evento è il lancio dello Sputnik, da cui scaturirà la corsa allo spazio e quindi un rinnovato interesse per la scienza, che diventa ancora una volta campo di scontro, diciamo così, all’interno della guerra fredda, esattamente come lo era stata durante la Seconda guerra mondiale.
Altro tema trattato è quello della censura: la guerra intrapresa dallo psichiatra Fredric Werham contro i fumetti, responsabili, a suo dire, di alcuni episodi di cronaca nera che coinvolgevano minorenni, aveva portato all’introduzione del Comics Code negli Stati Uniti. Questo «ebbe conseguenze devastanti», ma «paradossalmente, il Comics Code contribuì a iniettare più scienza e fantascienza nei fumetti», visto che la scienza era «un argomento ben visto dalla società». In Italia, la censura si spingeva fino a rimaneggiare le storie originali, ridisegnandone anche le vignette, per ridimensionare la violenza, modificare il linguaggio ritenuto non appropriato e, in caso, vestire con abiti meno sconvenienti le donne.
Il grande lavoro di studio di Bressanini è riconoscibile, per gli amanti dei fumetti, nello stile, che replica, a seconda dell’epoca in cui è ambientato il fumetto, proprio quello del periodo. È lo stesso Bressanini a raccontarci di aver «attinto a piene mani dai fumetti dell’epoca» e questo lavoro di “copiatura” è, al tempo stesso, un gioco, un omaggio ai grandi fumettisti e una strategia «per rendere più plausibile il falso storico» (e se non l’avesse dichiarato apertamente, forse ci saremmo cascati!). Le conoscenze dei fumetti sono arricchite dalla grande preparazione scientifica di Bressanini: nelle vignette, ritroviamo Feynman e Fermi, insieme a spiegazioni scientifiche che accompagnano gli eventi del fumetto.
Quello proposto da Bressanini è un percorso triplice: storico, scientifico e di costume (in tutti i sensi, visto che si fa riferimento a supereroi mascherati!). Le storie a fumetti aiutano a colpire meglio l’immaginario e a lasciare un segno nella nostra memoria, mentre i saggi di Bressanini permettono di focalizzare l’attenzione su ciò che, eventualmente, è sfuggito nella lettura del fumetto, sono una sottolineatura. Il fatto che Bressanini sfrutti due linguaggi diversi è una ricchezza: il libro può appassionare sia gli amanti dei fumetti, che i “soliti lettori” dell’amichevole chimico di quartiere, che lo ritrovano nell’”apparato testuale” che supporta i fumetti. Io credo che, con questo libro, Bressanini abbia superato sé stesso, forse perché traspare ancora meglio la sua passione, per la scienza e per i fumetti, forse perché, con la scelta di condividere anche l’«evento epocale» che ha sconvolto la sua vita, permette ai suoi lettori di conoscerlo ancora meglio e di sentirlo più vicino.
213 - 29 ottobre 2023
La matematica come esercizio di libertà
Nel blog di Sanoma Italia (azienda che racchiude importanti agenzie editoriali), è comparso un articolo scritto da Gianfranco Bo, autore del blog BASE Cinque, sempre molto ricco di spunti, di problemi da risolvere e di giochi matematici (più volte citato in questa newsletter). Gianfranco Bo è stato un docente di matematica e scienze alle medie e, in questo articolo, ci parla della libertà della matematica, attraverso, come esplicita il titolo stesso, alcuni problemi. L’inizio è dato da una citazione di Cantor: «L’essenza della matematica sta proprio nella sua libertà» e, parlandoci della libertà della matematica, Gianfranco Bo ci parla proprio della sua essenza. Un’essenza a volte difficile da comunicare, perché «il modo in cui si presenta la Matematica è molto diverso dal modo in cui si fa Matematica». Per riuscire a risolvere un problema nuovo, dobbiamo cercare un piano d’azione il più possibile personale, non lasciarci scoraggiare dagli errori e dai numerosi tentativi necessari, avere l’umiltà di chiedere aiuto o di collaborare con gli altri per giungere a una soluzione, combattere i blocchi mentali con i quali ci auto-limitiamo, e modificare i problemi che ci vengono proposti, fino a inventare qualcosa di nuovo. Prima di affrontarne la lettura, però, ricordiamo, con le parole di Gianfranco Bo, che «La parte più avventurosa, e più essenziale, della Matematica non è raccontata in nessun libro di testo, dalla scuola secondaria all’università: si impara strada facendo.»
Libertà e collaborazione a BergamoScienza
Realizzando i nostri laboratori per il Festival di BergamoScienza, abbiamo avuto modo di confrontarci con la libertà della matematica e anche con la necessità della collaborazione. In particolare, durante l’ultimo tratto di strada, con la preparazione della nostra Conferenza senza bordi, abbiamo potuto ridere con la matematica, lasciandoci coinvolgere e scoprendo anche nuove cose. Per quanto ci sia un po’ di rimpianto per non aver registrato quanto realizzato, ci siamo resi conto da subito che sarebbe stato davvero difficile rendere sia lo spirito con il quale abbiamo partecipato noi sia la reazione del pubblico presente in sala. Abbiamo realizzato la conferenza grazie alla collaborazione dei protagonisti che, nell’articolo, sono nominati come Prof# e Alunn#: abbiamo costruito insieme la scaletta, sulla base di quanto era stato esplorato nei mesi di progettazione dei laboratori, e ogni intervento è stato costruito sulla base del carattere e dello stile dei partecipanti. Questa numerosità di ruoli e queste differenze inevitabili tra i singoli protagonisti, sia nell’approccio alla topologia che nel modo di fare, hanno portato alla realizzazione di qualcosa di unico.
La speranza è che questo modo di affrontare la topologia, attraverso la risata e la presentazione di molti oggetti dal grande impatto (come il grande toro o la verifica della relazione di Eulero con solidi fatti di Polydron colorati), abbia lasciato un segno nella memoria dei presenti. La consapevolezza che le immagini riescono a incidersi meglio nella memoria è quella che guida il canale YouTube Mathematical Visual Proofs, che presenta, in questo caso, cinque classiche dimostrazioni senza parole: la somma di n numeri naturali, la scomposizione della differenza di quadrati, la somma dei numeri dispari, la dimostrazione del teorema di Pitagora e la serie infinita delle potenze positive di 1/2. La forza di questo canale non è data solo dal fatto che le immagini rendono più facile la memorizzazione, ma anche dalla citazione delle fonti, elencate e descritte sotto il video. Allo stesso livello anche il video legato alle tangenti di pi/8 e 3pi/8 (ovvero 22,5° e 67,5°), che è difficile tenere a mente e per le quali è sempre necessario ricorrere alle tavole goniometriche. Il canale LKLogic, invece, propone uno short con un trucchetto per calcolare in fretta il quadrato di un numero: per chi conosce il calcolo letterale e i prodotti notevoli è evidente che si usa il quadrato di binomio, ma è sempre bello vedere come la matematica compare sui social, in forma di trucchetti o semplificazioni per aiutare gli studenti nel calcolo.
Matematica e Web
Il 19 ottobre si è tenuto a Brescia, organizzato dalla Mathesis, il convegno “Dalla ricerca alla pratica: come è cambiata la didattica della matematica”. Invitata come autrice di un sito, ho scelto di parlare di Matematica e web: sfide e stimoli. Ho fornito la mia mappa personale di siti, blog, canali YouTube, podcast, persone, con le quali sono entrata in contatto negli ultimi anni (gli stessi che di fatto costellano le mie newsletter), e che mi hanno permesso di approfondire e far crescere sia la mia passione che la mia cultura matematica. Può sembrare che io l’abbia presa un po’ alla larga, visto che ho descritto il mio percorso, a partire dalla laurea in matematica, ma il motivo è presto detto: mi sono laureata un paio di mesi dopo la nascita di Google e ripercorrere la nascita (e la crescita) del web è stato importante per collocare, in qualche modo, la mia scelta di realizzare un sito, in un periodo in cui non era ancora una scelta così scontata. Probabilmente sembra di sentir parlare della preistoria visto che, attualmente, ci confrontiamo con ChatGPT e con l’intelligenza artificiale. Pochi giorni prima del convegno, ho avuto modo di ascoltare un webinar del prof. Domingo Paola, che ha parlato dell’utilizzo dell’intelligenza artificiale per l’insegnamento e per l’apprendimento della matematica. Interessante la citazione riportata all’interno di un articolo per MaddMaths! scritto a marzo: «[…] gli esseri umani disimpareranno l’arte di ricordare e dovranno sempre più affidarsi alla tua invenzione per richiamare le cose che sanno e quindi non saranno più autonomi nel disporre delle proprie conoscenze […] I discorsi, poi, una volta scritti, verranno letti da chiunque, senza che nessuno li possa spiegare […], così, invece di diventare più colta, la gente diverrà più ignorante e, nel contempo, presuntuosa». La citazione non fa riferimento all’intelligenza artificiale, visto che è presa dal Fedro di Platone: si parla, in questo caso, della scrittura, che si contrappone alla cultura orale diffusa fino a quel momento. Dopo aver portato a termine anche il corso Zanichelli L’Intelligenza Artificiale in classe ed aver provato a usare ChatGPT per realizzare piccoli compiti, ho scelto, durante una lezione di fisica in terza liceo scientifico, di proporre a ChatGPT uno dei primi esercizi del mio libro di testo sulla conservazione della quantità di moto. Ne sono nate riflessioni interessanti anche sul modo di gestire le interrogazioni e, in particolare, la fatica degli alunni nel gestire l’ansia quando non sanno rispondere alle domande proposte. Chiamati a dare un voto all’interrogazione di ChatGPT, i ragazzi non hanno potuto che riconoscerne l’inadeguatezza, e gli hanno dato una sonora insufficienza!
A caccia di voti
Mi pare particolarmente interessante la proposta alternativa alle classiche interrogazioni offerta da questo articolo di MaddMaths! La proposta è di Claudia Zampolini, insegnante di matematica e fisica presso il liceo scientifico “Galeazzo Alessi” di Perugia. Mi è già capitato di dire che il modo di interrogare di un insegnante rimanda all’idea della disciplina che l’insegnante stesso si porta dentro, e credo che questa proposta di Claudia Zampolini ci mostri l’importanza di valutare non sulla base di una fotografia, scattata in un unico momento, durante la tipica interrogazione, ma sulla base di un filmato, che registra il percorso fatto, e che permette, quindi, all’insegnante di registrare anche i tentativi e gli errori, i progressi e le difficoltà affrontate nell’apprendimento. Il docente può assistere come spettatore a questo percorso, tenere presente la tenacia e la determinazione dell’alunno nel raggiungere i propri obiettivi, incoraggiare e usare la valutazione per indirizzare il futuro, come indicato dal testo di Cristiano Corsini La valutazione che educa. «Queste esperienze sono nate con l’intento di ridurre lo stress degli studenti», ci ricorda Claudia Zampolini in chiusura, ma credo che potrebbe essere un’occasione per ridurre anche lo stress del docente.
A cosa serve la matematica
Il XXII Congresso dell’Unione Matematica Italiana si è svolto a Pisa dal 4 al 9 settembre scorsi, e ha visto al suo interno anche la realizzazione di un laboratorio pratico di comunicazione della matematica. In tale occasione, è stato possibile assistere all’intervento di Eduardo Saenz de Cabezon Irigaray, docente presso l’Università di La Rloja (in Spagna), Come parlare di matematica a un vasto pubblico. Eduardo Saenz è fondatore del canale YouTube Derivando, che conta 1,44 milioni di iscritti ed è online dal 2015. È del 20 settembre il video sul Teorema di Napoleone, che suggerisco (soprattutto se in classe avete già avuto occasione di parlare di omotetie): per quanto i video siano in spagnolo, per noi italiani risultano comunque facili da seguire e da comprendere, e la simpatia dell’autore rende tutto più leggero. Ho realizzato che mi ero già imbattuta nel matematico, in particolare nel suo intervento realizzato per TED nell’ottobre del 2014, A cosa serve la matematica. Di fronte alla terribile domanda che spesso gli insegnanti si sentono rivolgere (e non solo dai propri alunni), Eduardo Saenz non reagisce attaccando, dicendo cioè che la matematica ha un senso in sé e per sé, o difendendosi, e dichiarando che la matematica è alla base di tutto, ma, consapevole che entrambe le risposte sono vere, sottolinea che «Tutto quello che rende scienza la scienza è il rigore matematico». Da bravo comunicatore, Eduardo Saenz è riuscito a rendere immortale l’affermazione “Un teorema è per sempre” e il video, che nella tradizione TED ha anche la sua accurata traduzione in italiano, ci permette di gustarci tutte le motivazioni da lui usate per dimostrare la sua asserzione.
Halloween e matematica
Grazie a MathVisualProofs, possiamo rappresentare un fantasmino con Geogebra, usando le equazioni indicate, mentre Vihart ci parla delle lucine colorate: con lo stile che la contraddistingue, Victoria parla dei colori legati ad Halloween e, mostrando la sua fila di lucine colorate a forma di ragno con i colori verde, arancio e melanzana, ci fa vedere come il numero 3 sia il minimo per dare l’idea di un inseguimento lungo la fila di luci (con due soli colori avremmo invece, semplicemente, un’alternanza). A Natale possiamo invece associare quattro colori e, senza dubbio, 4 è il numero del Natale, come 3 è quello di Halloween! L’ultimo regalo legato a Halloween viene dal profilo Instagram Scienzalcubo, che realizza un fantasmino usando un becher, un cucchiaino di bicarbonato, un po’ di olio e qualche goccia di aceto: questo con la matematica non si sarebbe potuto realizzare!
Buona matematica! Ci sentiamo tra TRE settimane!
Daniela
PS: Immagine dal Post del 16 settembre
Moto rettilineo uniforme ottobre 2023
Verifica di fisica, classe seconda liceo scientifico.
Argomento: velocità.
Durata: 60 minuti.
Retta e piano cartesiano ottobre 2023
Verifica di matematica, classe terza liceo scientifico.
Argomento: piano cartesiano e retta.
Durata: 110 minuti.
Matematica e Web: sfide e stimoli
Intervento al convegno Mathesis di Brescia, “Dalla ricerca alla pratica: come è cambiata la didattica della matematica”, del 19 ottobre 2023
L’intento di questo intervento è quello di parlare del ruolo che può avere il Web nella nostra didattica. È, quindi, necessario che io faccia una breve storia del Web, anche se sarà una storia un po’ egocentrica, visto che è costruita “attorno a me”. Pare, da questa foto [la foto della mia laurea, mentre stringo la mano al mitico prof. Degiovanni!],

che parta un po’ da lontano, ma non spaventatevi! È il 6 novembre del 1998, il giorno della mia laurea! Quello stesso giorno, dopo la proclamazione, sono passata in segreteria per alcune carte e ho trovato questo:

Complice il fatto che un impiego come insegnante sembrava lontanissimo, ho deciso, seduta stante, di iscrivermi a un corso biennale di perfezionamento in didattica della matematica (era venerdì, e il corso cominciava il lunedì successivo), forse per paura di perdere il mio status di studente, o per paura di crescere. La verità è che questo corso mi ha dato grandissimi stimoli e una tale ricchezza che, a distanza di 25 anni, posso ancora attingere a quanto fatto.
Nel 1998 eravamo quasi tutti digiuni di Web e, tra le materie, c’era anche informatica. Ricordo ancora la lezione nel laboratorio: la prima ricerca online sul motore di ricerca Virgilio, un po’ più noto all’epoca rispetto a Google, nato da poche settimane.
Tutti i dispositivi collegati in rete, insieme agli apparati necessari per l’interconnessione, costituiscono Internet, abbreviazione di “internetworking”, un termine che risale alla Seconda guerra mondiale e che ha a che fare con le comunicazioni radio. Come spesso capita con i grandi progressi, anche Internet è nata in tempo di guerra, durante la guerra fredda per la precisione: gli Stati Uniti d’America, negli anni Sessanta, erano alla ricerca di un nuovo sistema di difesa e di controspionaggio e Internet costituiva una facilitazione nelle comunicazioni.
Come tutti sappiamo, al CERN, sul finire degli anni Ottanta, c’era invece il problema della gestione delle informazioni: i fisici avevano bisogno di condividere i dati e Tim Berners-Lee propose una rete globale di documenti HTML. Robert Caillau, che creò il logo WWW World Wide Web, supportò entusiasticamente l’idea di Berners-Lee e creò il primo browser per Mac. Il CERN non mostrò, però, un grande entusiasmo per il loro progetto, anzi: dichiarò che si trattava di un uso improprio delle risorse e che, non rispondendo ai fini del CERN, non aveva senso spendervi del denaro. Fu così che nel 1992 Tim Berners-Lee si trasferì al MIT. Ad aprile del 1993, il CERN concesse l’uso del Web a chiunque, gratuitamente e nel 1995 gli utenti connessi erano ormai 18.000.000. Il 1995 è l’anno della nascita di quei giganti di Amazon e Ebay e, nel 2004, Tim O’Reilly parla della fine del Web statico e della nascita del Web 2.0, che vede un ruolo attivo dell’utente. Per realizzare i primi siti web, era necessaria la padronanza dell’HTML, ma ad un certo punto, chiunque, anche senza una preparazione tecnica adeguata, poteva realizzare il proprio blog e, quindi, contribuire a modellare il Web. Non solo…
Tra il 1997 e il 2000 è attivo il primo social, SIXDEGREES, ispirato alla teoria dello scrittore ungherese Frigyes Karinthy formulata in un racconto del 1929, secondo la quale ogni persona può raggiungere chiunque nel mondo con non più di sei passaggi, ovvero di cinque persone come tramite. Con i suoi 3,5 milioni di utenti, il primo social è un po’ piccolino, ma, rispetto ad oggi, sono pochi anche gli utenti della rete. Nel 2003 fa la sua comparsa Linkedin, che conta 930 milioni di utenti, nel 2004 Facebook, che ora conta 3 miliardi di utenti, e nel 2006 Twitter, con 1,3 miliardi di utenti e un logo che ricorda i simboli matematici per gli insiemi numerici.
Nel 1998, all’epoca del corso biennale, il Web era un grande ipertesto, qualcosa di più ricco e complesso di un libro, insomma, potenzialmente motivante e stimolante per gli alunni.

Questo è l’estratto di un documento scaricato da internet e stampato il 26 novembre del 1998 (o ra purtroppo irreperibile).
Il corso biennale non aveva solo l’obiettivo di darci strumenti all’avanguardia per entrare in classe, ma anche di farci riflettere sulla necessità di uno spessore culturale. La prof.ssa Maria Paola Negri (all’epoca docente di filosofia, storia e scienze dell’educazione presso l’Università Cattolica del Sacro Cuore) ha scelto di citare Einstein, che, nominando il filosofo scozzese David Hume e il fisico e filosofo austriaco Ernst Mach, ricordava come le idee nascano dai terreni più strani, purché siano fertili: «A chi mi chiede quando per la prima volta pensai alla teoria della relatività, rispondo: leggendo le opere di Hume e Mach.»
Tra le materie del corso c’era anche una riflessione sull’apprendimento, guidata dal prof. Alessandro Antonietti, attualmente preside della facoltà di Psicologia dell’Università Cattolica di Milano. Egli stimolò la riflessione di noi insegnanti sulla matematica, ci invitò a pensare che cosa questa materia rappresentasse per noi e compilammo, quindi, la nostra personale mappa della matematica: dopo aver scritto su un foglio “matematica” al centro, attorno scrivemmo tutte quelle cose che nella nostra mente si collegavano ad essa. E scoprimmo che per noi la matematica non era davvero solo una questione di numeri: gli alunni possono vederci numeri e operazioni, magari emozioni (in genere negative!), ma noi ci possiamo vedere estetica e arte, cogliamo le relazioni, e la vediamo ovunque, anche in contesti apparentemente lontani.
Il web, ad esempio, trabocca di matematica, perché funziona grazie alla matematica, ma anche perché sono numerosissimi i contenuti di matematica che possiamo trovare. Da Salvatore Aranzulla, al blog Mathone, (del centro studi A. Manzoni), attualmente ci sono parecchi elenchi di siti e basta cercare “esercizi matematica” per ottenere, in meno di mezzo secondo, oltre 15.000.000 di risultati. Ed è lo stesso risultato a cui possono accedere i nostri alunni… La situazione è cambiata completamente nel 2020, sia a livello di quantità di contenuti, sia a livello di didattica: la rivoluzione che abbiamo portato avanti, consapevolmente o meno, nelle nostre aule virtuali (più probabilmente nel salotto di casa nostra) ha cambiato tante cose e le tre icone delle principali piattaforme usate da tutti noi con la DAD non hanno certo bisogno di essere presentate.
Anche per questo, il panorama era completamente diverso nel 2006: sembra quasi di parlare della preistoria…
Dopo un corso di aggiornamento a scuola, durante il quale ci era stata presentata una piattaforma grazie alla quale condividere materiali e documenti con i ragazzi, rendendomi conto dell’impossibilità, per la mia scuola, di realizzare questa cosa così futuristica, decido, insieme a mio marito e su suggerimento di un’amica, di dare vita a un mio sito internet, con il quale, appunto, condividere materiali.
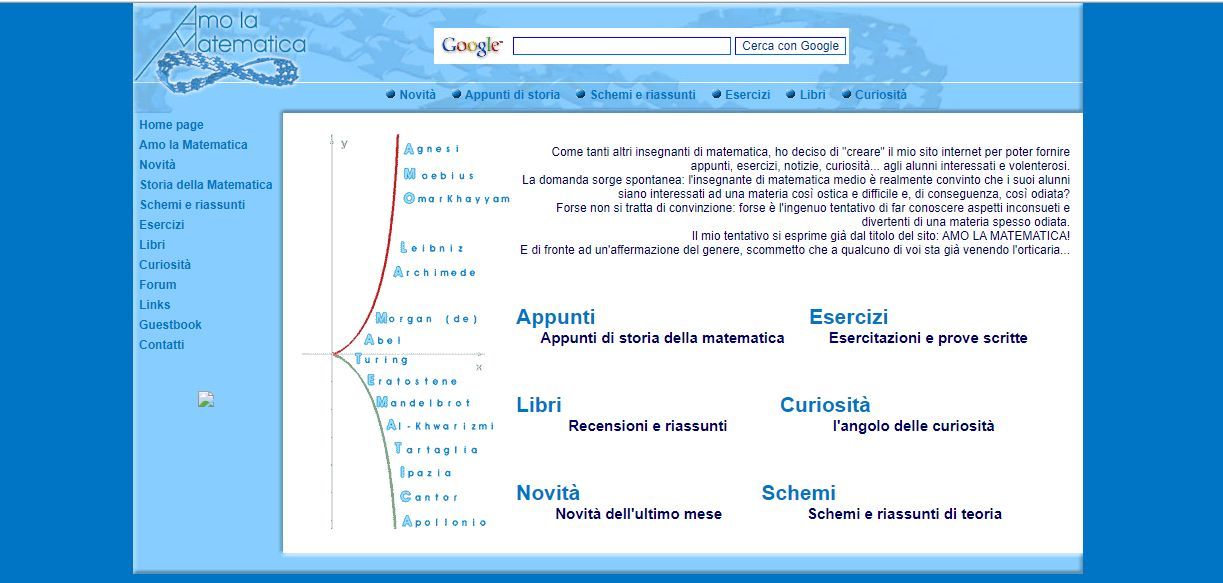
Ad agosto del 2006, il mio sito comincia il suo percorso e due sono i miei obiettivi:
- Condividere materiali con gli alunni, come appunti e schemi, verifiche ed esercizi
- Condividere cultura, attraverso recensioni di libri e curiosità
All’epoca non erano molti i siti di matematica, anzi: non erano molti i siti in generale! Ma anche gli alunni non avevano grandi possibilità tecnologiche: i miei alunni andavano in biblioteca per poter accedere al sito o per scaricare la posta elettronica, e facevano stampare le verifiche ai genitori in ufficio. Nel giugno del 2007 il primo iPhone è stato lanciato sul mercato e a partire dal 2010, questo strumento ha raggiunto anche i nostri studenti (a volte prima ancora di diventare di nostra proprietà!).
Ho deciso di presentarvi la mia personale rassegna di contenuti, che va ben al di là degli esercizi di matematica che si possono trovare online. Immaginando che ognuno di voi, a seconda dell’indirizzo in cui insegna, abbia la propria sitografia, in merito a contenuti scolastici, quello di cui voglio parlare oggi va al di là dei contenuti scolastici. Va ad incidere, appunto, sulla cultura matematica.
Comincio dall’inizio, ovvero dal febbraio del 1999, con Francesca Ortenzio, Piero Fabbri e Rodolfo Clerico, meglio noti come i Rudi Mathematici. Da febbraio del 1999 i tre amici, che lavorano totalmente a distanza, visto che abitano lontani tra loro, si occupano della pubblicazione di questa rivista elettronica, che con il proprio nome richiama i Ludi mathematici di Leon Battista Alberti e il soprannome di Rodolfo Clerico, Rudy. Il logo stesso della rivista trasuda cultura: il disegno è di Maurits Cornelis Escher e la scritta è una citazione di Pierre de Fermat e del suo celebre “Ultimo teorema”. La rivista arriva in circa 3000 caselle di posta elettronica ogni mese, tutt’altro che puntuale, ma accompagnata da una simpatica mail. Da qualche anno ha ampliato i propri orizzonti con una rubrica sul blog di Le Scienze e sulla rivista Le Scienze.
Procedo con Maurizio Codogno, che ha aperto il suo blog Notiziole di .mau. a settembre del 2001. Maurizio (che ha una voce Wikipedia tutta per lui, scritta in dialetto milanese!) è un informatico e il suo blog è una vera miniera, dato che scrive tantissimo: commenta le notizie, recensisce libri, propone giochi matematici, e, come in un diario, ci racconta ciò che fa (è così che ho scoperto di averlo incontrato nel corso dell’ultimo Festival della Fotografia che si è tenuto a Capo di Ponte). L’ultimo post è dedicato alla parabola che aiuta a fare le moltiplicazioni, scoperta al Mathematikum, il museo di Gieben.
Maurizio Codogno è anche l’ideatore e l’anima del Carnevale della matematica. Il carnevale è attivo dal 14 maggio 2008 e viene ospitato sul sito di uno dei partecipanti il 14 di ogni mese (così anche i Rudi sono obbligati ad essere puntuali!). A parte la pausa estiva, il Carnevale non si è mai interrotto ed è alla sua 172^ edizione (ospitata da Maurizio Codogno). Il carnevale ha alcune particolarità: si tratta di un gruppo di divulgatori che sceglie di pubblicare un articolo (ma spesso più di uno) attorno al tema proposto da chi ospita il carnevale. Ogni Carnevale si apre con una cellula melodica, musicata da Flavio Ubaldini, in arte Dionisoo, e scritta da Marco Fulvio Barozzi, in arte Popinga, che ha ideato la celebre poesia gaussiana: fattorizzando i numeri composti e associando a ogni numero primo un verso, è possibile ottenere una poesia.
A fine marzo 2009 fa la sua comparsa MaddMaths!, un enorme contenitore riempito da numerosi divulgatori. Nella slide ho riportato la foto di Roberto Natalini, ideatore del progetto, matematico e Direttore dell’IAC-CNR (Istituto per le Applicazioni del Calcolo “Mauro Picone”), Stefano Pisani, matematico e uno degli autori del sito satirico Lercio, Alberto Saracco, docente dell’università di Parma e “matematico prestato alla Disney”, e Marco Menale, autore della rubrica La lente matematica.
Spin off di MaddMaths! sono due podcast: il primo, Le maschere del Carnevale Matematico, è realizzato periodicamente da Fabio Quartieri, studente di matematica a Bologna, arrivato ormai al suo undicesimo episodio. Si tratta di interviste a “docenti, ricercatori, matematici che vogliono raccontare la matematica per renderla più accessibile a tutti”. È un raccoglitore di esperienze, ma soprattutto di passione.
Iheart, invece, è una serie di cinque podcast, nei quali Alfio Quarteroni racconta la matematica che ha permesso di realizzare un modello del cuore e di studiarlo meglio. Scopriamo così matematici che parlano di cardiologia e cardiologi che parlano di matematica.
Mr Palomar è un altro dei blog storici: deve il suo nome alla passione di Paolo Alessandrini per Italo Calvino. Paolo è attivo anche su YouTube e è uno scrittore molto prolifico: ha cominciato con Matematica Rock, dedicandolo alla sua passione, la musica, ha proseguito con Bestiario matematico, e l'ultimo, in ordine di tempo, è Matematica in campo, dedicato al calcio.
Taxi 1729 è una società che si occupa di comunicazione scientifica. Attivi dal 2014 con 1251 eventi all’attivo (come dichiarato sul loro sito), che spaziano tra video divulgativi, live streaming, talk spettacolo, momenti di formazione, esposizioni interattive. Gioco d’azzardo, economia e sostenibilità sono i temi che vengono affrontati. Taxi 1729 è un chiaro riferimento a Srinivasa Ramanujan, il famoso matematico indiano. Durante la sua collaborazione con Godfrey Harold Hardy, agli inizi del Novecento, ricoverato in ospedale, ha ricevuto la visita di Hardy, che non era molto abile nella chiacchiera leggera, perciò gli ha parlato di un taxi che aveva come numero 1729. E ha commentato: “Che numero insulso!” Ramanujan ha, invece, ribadito che si tratta del più piccolo intero esprimibile come somma di due cubi, ovvero 10 e 9, 12 e 1.
Victoria Hart: se vi siete imbattuti nei suoi video, non potete averli dimenticati! Sono uno più bello dell’altro: io l’ho conosciuta attraverso i suoi video sui frattali, tutti accompagnati da una chiacchiera infaticabile, mentre disegna e accompagna il disegno matematico con il canto, perché lei è una “mathmusician”, una matmusicista. Figlia di due matematici, ha scoperto la sua passione a 13 anni e ha scelto di coltivarla in modo davvero originale.
Nel 2011, Google commissionò la creazione di 100 canali YouTube per aumentare il traffico sulla piattaforma, che aveva acquistato nel 2006 (e che era nata nel 2005). Per la matematica venne coinvolto Brady Haran e lui scelse di raccogliere la sfida. Per il nome, scelse di proposito di evitare il termine matematica, per minimizzare il riferimento alla scuola, ma la scelta cadde su un termine che richiama l’amore per i numeri, un canale “filonumerico” potremmo dire, Numberphile. Ci sono video di tutti i tipi, da Cédric Villani che parla delle medaglie Fields, a Tadashi Tokieda che fa vedere un cerchio che passa attraverso un buco quadrato, che ha la diagonale minore del diametro del cerchio, o Cliff Stoll che parla delle sue mille bottiglie di Klein nascoste nel seminterrato di casa sua. E c’è pure un video bellissimo, dedicato a pi greco, lungo, ovviamente, 6 minuti e 28 (un chiaro rimando a 2pi), con il quale gli autori mostrano la realizzazione di un miglio di pi greco, con un milione di cifre di pi greco.
Il MATH-segnale è un canale assolutamente da seguire: Davide Calza e Riccardo Moschetti hanno una preparazione fuori dal comune, una grande simpatia e un’abilità grafica che rendono molto facile seguire anche i contenuti più complessi. Ci sono alcuni video che sono imperdibili, come i due dedicati ai grafi, uno per giocare a guardie e ladri e l’altro per trattare la divisibilità in un modo diverso dal solito. Poi ci sono i video realizzati sulla spinta di scoperte recenti, come la nuova dimostrazione del Teorema di Pitagora ad opera delle due studentesse statunitensi: Davide e Riccardo hanno spiegato con chiarezza e senza risparmiarci alcun passaggio, in modo da guidarci sani e salvi alla meta.
Non potevo non concludere con Ilaria Fanelli, autrice del canale IlariaF Math: il suo entusiasmo e la sua passione sono trascinanti, perché con le sue idee Ilaria coinvolge un sacco di persone, non lavora da sola. Così abbiamo gli shorts “Che cosa è per te la matematica?”, che ha realizzato durante Strambinaria, ma che di fatto aveva già cominciato a coltivare tempo fa, quando apriva le sue serate, intervistando divulgatori matematici e non solo, proprio con questa domanda. Troviamo la risposta dei Rudi Mathematici, quella della matematica Roberta Fulci, redattrice e conduttrice di Radio3Scienza, finalista del premio Science Book of the Year con “Il male detto”, quella entusiasta di Federico Benuzzi, e, ultima in ordine di tempo, la risposta meno entusiasta di Federica Gerini, laureata in Biologia della Conservazione, che lavora nell’ambito della comunicazione per Musei e associazioni di protezione della Natura: ha definito la matematica un incubo! Altro grande lavoro di Ilaria, che è un vero catalizzatore di passione, è la sfida #peopleformath Ci sono già state due edizioni e l’elenco dei matematici raccontati dai vari divulgatori sta diventando importante. Ma Ilaria lavora anche parecchio alla divulgazione: sul suo canale si trovano video per giocare e video per approfondire, come la serie dedicata a Dante e la matematica.
Nel post Che cos'è Maddmaths! possiamo leggere: «La matematica è un po’ la bestia nera di tutti gli studenti e non ha una buona reputazione presso il cittadino medio, nonostante gli sforzi, spesso eroici, di alcuni insegnanti validi e preparati che cercano di presentare questa materia in un modo più vivo e attraente. [...] Per questo, a partire dal 2008, nell’ambito delle iniziative della SIMAI (Società Italiana di Matematica Applicata e Industriale) abbiamo cercato di immaginare un percorso che contribuisse a cambiare questo stato di cose, perché crediamo che la matematica sia oggi una delle risorse principali della tanto decantata innovazione tecnologica e per questo sia necessario rimuovere i pregiudizi esistenti contro questa disciplina.»
Ilaria Fanelli dichiara, nella sua home: «Le motivazioni che mi hanno spinto sono molteplici: in primis la volontà di mostrare il lato curioso e affascinante della matematica agli appassionati e ai non addetti ai lavori, offrire agli insegnanti spunti didattici e divulgativi da utilizzare nelle proprie classi e creare una community di persone che possano collaborare tra loro anche a distanza.»
La mia homepage, all’inizio di questa avventura, riportava questo messaggio di benvenuto: «Come tanti altri insegnanti di matematica, ho deciso di “creare” il mio sito internet per poter fornire appunti, esercizi, notizie, curiosità… agli alunni interessati e volenterosi. La domanda sorge spontanea: l’insegnante di matematica medio è realmente convinto che i suoi alunni siano interessati ad una materia così ostica e difficile e, di conseguenza, così odiata? Forse non si tratta di convinzione: forse è l’ingenuo tentativo di far conoscere aspetti inconsueti e divertenti di una materia spesso odiata. Il mio tentativo si esprime già dal titolo del sito: AMO LA MATEMATICA! E di fronte ad un’affermazione del genere, scommetto che a qualcuno di voi sta già venendo l’orticaria…»
Il titolo del sito, negli anni, mi ha regalato piacevoli siparietti: quando fornisco il mio indirizzo email, Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo., do il via a commenti di tutti i tipi, dal (purtroppo) tipico “Ho sempre odiato la matematica” al più simpatico “Mi è sempre piaciuta, ma poi ho preso altre strade”. Ma anche quando mi viene raccontato l’odio per la matematica, è un sentimento venato di rimpianto, che potrebbe essere ben espresso dalle parole di Mickaël Launay (che campeggiano ora nella mia homepage): «Non la amiamo, eppure ci piacerebbe amarla».
C’è da dire che, da quando esiste, il mio sito ha obbligato i miei studenti a dire, almeno una volta, “Amo la matematica”, oppure, per usare un’espressione dialettale (tipica sia del dialetto bresciano che di quello bergamasco – per onorare le capitali della cultura 2023): “Amò la matematica?!”, che non è il passato remoto del verbo amare, ma “Ancora la matematica?!”, come a dire: Ci hai stancato! Ne abbiamo abbastanza!
Energia ottobre 2023
Verifica di fisica, classe terza liceo scientifico.
Argomento: lavoro ed energia.
Durata: 70 minuti.
Verifica di recupero per assenti svolta il 17 ottobre
Conferenza senza bordi
Conferenza senza bordi: Topologia è…
Pc collegato al proiettore, sullo schermo è aperto un file Power Point con una bella copertina: sullo sfondo immagini di topologia, in evidenza la scritta: “Conferenza senza bordi: Topologia è…” e la data.
Il tavolo con il pc è invaso da oggetti topologici
Sale sul palco la Prof1:
Prof1: Buonasera a tutti e benvenuti! Siamo qui, questa sera, per parlarvi di topologia, l’argomento dei nostri laboratori di BergamoScienza. Purtroppo, hanno chiesto a me di parlarvene, ma io all’Università non ho sostenuto l’esame di topologia. Perciò (la diapositiva successiva recita: “Grazie per l’attenzione!”), vi saluto e vi ringrazio per aver partecipato.
Scende dal palco e se ne va.
Il palco resta vuoto.
Attimo di silenzio.
Dubbi.
Perplessità.
La Prof2, alzandosi dalla prima fila, prende la parola:
Prof2: Scusate! Temo che ci sia stato un piccolo malinteso con la Prof1. Non erano questi i patti…
Proverò a dire qualcosa io della topologia, anche se ne ho un pessimo ricordo dall’università: il professore mi ha bocciato per due anni consecutivi a tutte le sessioni e non ho imparato nulla. Ci provo!
La Prof2 sale sul palco, mentre qualcuno si avvicina al pc e cambia la presentazione, inserendo una nuova chiavetta:
Comincerei dallo spiegarvi cosa significa “conferenza senza bordi”. La topologia è una parte un po’ originale della matematica, tanto che viene chiamata “geometria del foglio di gomma”. Io comincerei con questi due anelli: dal posto non li vedete molto bene, perciò, inviterei qualcuno di voi sul palco a darmi una mano (Prof2 chiama Alunn01, prende dal tavolo la striscia di carta e gliela passa, poi confabula con Alunn01, fingendo di spiegare cosa deve fare). Prendete una striscia di carta: se incollate gli estremi tra di loro, ottenete un cilindro e, come potete vedere (Alunn01 mostra la cosa avvicinando i due estremi) ha una superficie interna e una esterna. Adesso, incolliamolo facendo fare una torsione di 180° a uno dei due estremi (Alunn01, intanto, collega con la cucitrice i due estremi): quello che otteniamo è un nastro di Mobius, un nastro che NON ha un dentro e un fuori, perché ha un’unica superficie. Ora prendiamo una seconda striscia e realizziamone un altro, ruotando l’estremo in senso opposto (Alunn01 procede e vengono mostrati i due nastri. Prof2 prende dal tavolo due fogli bianchi) Se prendo due fogli bianchi qualsiasi, di forma rettangolare, riconosciamo tutti che hanno quattro lati [1]: se li uniamo lungo un lato, entrambi i fogli perdono un lato, ma se uniamo due nastri di Mobius… beh! Ogni nastro di Mobius ha un solo lato quindi se io unisco due nastri lungo l’unico lato che hanno… ottengo una bottiglia di Klein che è una bottiglia speciale, visto che non ha bordi, non ha dentro e fuori e non si può riempire. Ecco il motivo per cui questa sarà una conferenza senza bordi, perché non ci sarà qualcuno che parla e qualcuno che ascolta, ma chiunque potrà intervenire, se ha qualche curiosità o se vuole dire qualcosa sulla topologia.
Entra Alunn02 e prende la parola:
Alunn02: Direi che è ora di mostrare realmente come si svolgerà questa conferenza e cos’è la topologia. Comincerei con una sfilata del Topo-outfit, la linea di moda alla quale abbiamo lavorato quest’anno: Alunn03, tocca a te!
Alunn03 entra con i pantaloni, sul lato arancio, un toro rosso in testa e il nastro di Mobius enorme a tracolla, una bottiglia di Klein all’uncinetto in una mano come una borsetta e al polso un nastro di Mobius come bracciale
Alunn02: Come vedete, Alunn03 indossa degli originalissimi pantaloni topologici. Ma in cosa consiste la loro originalità? Non solo nel colore, non certo nella forma (Alunn03 allarga i pantaloni per mostrarne la grandezza), ma nel fatto che, se io chiedo a Alunn03 di mettere a rovescio i pantaloni, lo può fare anche in pubblico, perché non ha bisogno di toglierli! Prego, Alunn03! [2]
Alunn03 procede a rovesciare i pantaloni mentre Alunn02 lo accompagna: A molti di voi sarà capitato di macchiare i pantaloni e di non avere la possibilità di cambiarli. Questa potrebbe essere la soluzione! Mettendoli a rovescio, anche la macchia verrà nascosta! Come vedete, si tratta di un capo molto originale, realizzato con una, anzi due stoffe morbide ed elastiche, in modo che possa essere indossato da chiunque. Certo, per poter rovesciare i pantaloni bisogna essere un po’ elastici e…
Entra Prof3, con dei libri sotto il braccio, vestito come un professore serio. Interrompe Alunn02 e comincia a parlare:
Prof3: Non è possibile! Ma voi davvero pensate di poter parlare di topologia in questo modo? Andatevene, per favore (e caccia i due dal palco), qui la gente vuole ascoltare qualcosa di serio. Sarà meglio che prenda in mano io la situazione. Buonasera, mi presento: sono Prof3, ex studente del Celeri, e laureando in fisica delle interazioni fondamentali all’Università degli studi di Padova. (si avvicina a pc per mettere una chiavetta e far partire una presentazione e anche chi aveva la postazione a pc si allontana preoccupato). La nobile branca della topologia serve per capire i segreti del nostro universo, dalle cose più grandi come gli astri e le galassie alle cose più piccole come le particelle subatomiche. Prendiamo due buchi neri, oggetti così pesanti che la loro gravità attrae a sé qualsiasi cosa, perfino la luce. Se sono abbastanza vicini, finiranno per fondersi in un solo grande buco nero. Ed ecco che finalmente la forma che volgarmente hanno chiamato “pantaloni” ora ha un significato scientifico importante! Ma non è finita qua: se leggiamo questa figura al contrario, il modello standard, e volendo anche le teorie più recenti e straordinarie come la teoria delle stringhe, ci dicono che questa figura rappresenta una particella che a un certo punto si divide in due particelle più piccole. E questi fenomeni servono non solo alla fisica, ma alla medicina, all’ingegneria e a tutte le scienze! E potrei andare avanti con altri mille esempi, come lo spin delle particelle paragonato al nastro di Moebius, oppure…
Mentre Prof3 sta concludendo, entra Alunn04, portando un vassoio, sul quale sono presenti una tazza, una teiera e una ciambella. Alunn04 prima offre la tazza vuota a Prof3 (che si ferma perplesso in mezzo a una frase) e poi comincia a versare del liquido nella ciambella, al che Prof3 la ferma: [mentre avviene questo scambio, chi era a pc torna in postazione e fa partire la slide successiva della prima presentazione]
Prof3: Ma cosa stai facendo?
Alunn04: Beh, voi topologi non dite forse che una tazza e una ciambella sono la stessa cosa? Stavo versando il tè nella ciambella e le stavo dando la tazza da mangiare…
Entra allegra Alunn05 portando con sé una palla pelosa:
Alunn05: Se si parla dell’umorismo dei topologi, allora tocca a me! Sono qui per parlarvi del teorema della palla pelosa, dimostrato dal matematico olandese Brouwer nel 1912! (nel frattempo, Prof3 se ne va mostrando esasperazione e Alunn04 abbandona il palco) «Il teorema ci dice che, se abbiamo una palla pelosa come questa, non è possibile pettinarla in modo continuo in una stessa direzione, senza che ci siano peli che vanno nella direzione sbagliata o punti non pettinati come questo punto qua. Questo teorema […] può essere applicato anche al nostro pianeta, infatti possiamo considerare, anziché la direzione dei peli, la direzione del vento e il teorema in questo caso ci dice che sulla Terra esiste sempre un punto, come questo qua, in cui non c’è minimamente vento.» [3]
Entra, chiaramente infastidito, il Prof4, vestito da serioso professore e prende la parola:
Prof4: Ma non è possibile! Non si può parlare della matematica in questo modo, come se si trattasse di una barzelletta da raccontare! (Caccia Alunn05dal palco) Innanzi tutto, scusa collega (rivolgendosi alla Prof2), mi pare che tu sia stata un po’ imprecisa su quella cosa del “senza bordi” (sarcasticamente). Forse è bene che chiarisca il concetto per il nostro pubblico. Ho giusto predisposto un paio di slide in proposito... (fa un cenno e subito vengono proiettate le foto delle dispense di topologia, in cui viene “descritto” come ottenere cilindro, nastro di Möbius, toro e bottiglia di Klein a partire da un quadrato). Partiamo considerando un quadrato, o un rettangolo, tanto sono spazi topologici omeomorfi. Come si evince chiaramente dalle immagini mostrate, è possibile quozientare il quadrato chiuso, ovvero [0,1]×[0,1], mediante relazioni di equivalenza opportunamente definite, per ottenere altri spazi topologici: ad esempio, se definiamo la relazione di equivalenza ρ mediante la partizione formata, per ogni punto Y di un lato verticale, dalle coppie {Y,Y^'}, con Y' simmetrico di Y rispetto all’asse di simmetria verticale, e dai singleton {X} per ogni altro punto X del quadrato, lo spazio quoziente [0,1]^2/ρ è omeomorfo al cilindro, cioè S^1×[0,1]. Il cilindro non risolve tuttavia la questione del togliere i bordi, dato che ha frontiera omeomorfa all’unione di due circonferenze distinte, come neppure il nastro di Möbius, dove il bordo è evidentemente omeomorfo a S^1 (sguardo di rimprovero alla Prof2)... se però consideriamo la naturale relazione di equivalenza che identifica anche i lati orizzontali, ciascuno percorso nel verso positivo, allora il quoziente che si ottiene è chiaramente omeomorfo a un toro, cioè al prodotto cartesiano della 1-sfera con se stessa, che ha frontiera topologica vuota, anche senza scomodare la bottiglia di Klein, che pure in effetti è un quoziente del quadrato, mediante la relazione...
Alunn01, dal posto, alza la mano e, togliendogli la parola, esclama: Io non ho capito niente, me lo può rispiegare?
Si alza dal pubblico la Prof5 e cerca di risolvere la questione
Prof5: Prof4, se non è un problema, provo io. (Rivolgendosi al pubblico) Prendiamo un rettangolo (o un quadrato, visto che per la topologia sono la stessa cosa) e ripieghiamolo su sé stesso. (procede a realizzare davvero quanto dichiarato, con un foglio rettangolare) Come vedete, otteniamo un cilindro. Ora ripieghiamolo di nuovo e facciamo combaciare i due estremi: quello che otteniamo è un toro, quello che i non matematici chiamano ciambella. (prendendo in mano un mega-toro realizzato con la stoffa) Eccone qui una versione in stoffa, un po’ più grande per rendere l’idea! In ogni caso, avrete notato che da un foglio con quattro bordi, siamo passati a un oggetto che non ha alcun bordo!
Prof4: (impaziente) Va bene… immagino che forse così possa essere chiaro, per un pubblico non esperto.
Prof5: Volevo concludere raccontando che recentemente è stato dimostrato un risultato di topologia molto importante, che era stato enunciato nel 1977, perciò ci sono voluti quasi cinquant’anni e…
Interviene Alunn06, timidamente, salendo sul palco con in mano il nastro di Moebius che è una riproduzione all’uncinetto del celebre nastro di Escher:
Alunn06: Mi scusi, Prof5, credo che ora tocchi a me, visto che lei sta parlando da un po’. (Rivolgendosi al pubblico) Vorrei mostrarvi questo bellissimo nastro di Mobius, realizzato a uncinetto seguendo il disegno di Escher, che tutti, credo, conosciamo (alle spalle compare l’immagine del dipinto di Escher). La cosa interessante di questo nastro è che non è il classico nastro di Moebius: se notate, è arrotolato su sé stesso ben due volte e…
Entra, prepotentemente, Alunn07:
Alunn07: Ma cosa c’entra adesso il liceo artistico? Stiamo parlando di matematica e tirate fuori queste cose artistiche. Io direi che è ora di cominciare a fare i seri. Sapete, i matematici vedono sé stessi come dei poeti sognatori, mentre gli scienziati usano la matematica come uno strumento, utile per ottenere un risultato. La verità è che hanno ragione tutti! Pensiamo alla teoria dei nodi, che è una branca della topologia: questa parte è nata per risolvere un problema scientifico. Prima della scoperta degli atomi, alcuni scienziati, tra i quali Lord Kelvin, credevano che la materia, chiamata etere, fosse fatta di nodi e garbugli. Quindi, hanno cominciato a classificare i singoli nodi (alle spalle compare l’immagine della tavola dei nodi), per poi rendersi conto che non era un modello adeguato. Allora hanno perso interesse, conquistati dalla nuova teoria degli atomi, che era effettivamente quella corretta. I matematici, però, persone un po’ strane come avrete capito, trovarono nei nodi un simpatico passatempo e continuarono a sviluppare questa teoria, che sembrava non avere alcuna utilità. [4] La scienza, inaspettatamente, ad un certo punto ha avuto bisogno di questa teoria, perché… perché… forse è meglio che lasci la parola alla Prof6, docente di scienze del nostro istituto, che potrà spiegarci cosa intendo. (Invita a salire sul palco la Prof6).
La Prof6 sale sul palco e comincia a parlare:
Prof6: Se ci venisse chiesto di disegnare il DNA molti di noi disegnerebbero una scala a chiocciola, la famosa doppia elica. Gruppi alternati di fosfati e di zuccheri sono il corrimano della scala, mentre le coppie delle quattro basi complementari, adenina, timina e citosina, guanina, formano i gradini della scala.
La struttura di basi si chiama struttura primaria, la doppia elica, invece, struttura secondaria.
La lunghezza del DNA si misura in termini di coppie di basi: il DNA umano è lungo circa 3 miliardi di coppie, quello del batterio più comune, l'Escherichia Coli, solo 4,4 milioni di basi.
Nel 1981 grazie ad una tecnica chiamata elettroforesi si giunse alla conclusione che la lunga molecola del DNA ha anche una struttura terziaria, che consiste in un ulteriore avvitamento nello spazio, un po’ come il filo della cornetta del telefono che dopo un lungo utilizzo, assume una struttura super-inanellata, aggrovigliandosi su sé stesso. Quindi il DNA, nel nucleo della cellula, si trova tutto aggrovigliato e compattato in uno spazio piccolissimo e, in alcuni casi, addirittura sotto forma di anello. In queste condizioni, può capitare che si formino nodi, pieghe e intrecci che hanno ripercussioni anche molto negative sulla funzionalità della cellula. (Al lato del palco si mettono Alunn04 e Alunn05: Alunn04 si siede sull’angolo del palco e Alunn05 prima prende le due trecce e le avvolge a elica, poi le compatta creando una specie di chignon. Prof6 fa un cenno affermativo) Infatti, durante la replicazione e la trascrizione, la doppia elica si deve aprire per permettere l’accesso agli enzimi. Separare due semi-eliche che sono super inanellate, talvolta addirittura formando uno o più nodi, è un problema molto complesso oltre che molto interessante. (A questo punto Alunn05 disfa una treccia ad Alunn04, poi cerca di pettinarla, ma sembra che trovi davvero un sacco di nodi… è peggio di una palla pelosa!) Esistono degli enzimi in grado di sciogliere gli eventuali nodi del DNA e riportare la doppia elica a una configurazione più stabile, questi enzimi sono chiamati topoisomerasi. Ed è proprio qui che entra in gioco la teoria dei nodi; infatti, grazie ad essa e alla topologia si possono creare dei modelli con cui validare o smentire ipotesi su come funzionano le topoisomerasi. [5]
Al termine della presentazione della Prof6, interviene Alunn06:
Alunn06: Mi scusi, professoressa, posso aggiungere una cosa? Vorrei dire che i nodi non sono proprietà solo della scienza, ma anche dell’arte. A me, parlando di nodi, vengono in mente gli anelli di Borromeo (sullo sfondo si apre l’immagine di un nodo borromeo): sono «un esempio di link con tre componenti, ciascuna delle quali è un nodo banale (cioè un anello semplice) e “link borromeo” (più erroneamente ma comunemente detto “nodo borromeo”) deve il suo nome proprio al simbolo araldico fatto risalire alla persona di Federico Borromeo, cardinale e arcivescovo di Milano, che lo scelse appunto come suo emblema, simbolo della dinastia borromea e, data la sua religiosità, i tre anelli potrebbero rappresentare anche la trinità cristiana.» [6] Realizzarlo è molto semplice: basta prendere due anelli disgiunti e poi legarli con un terzo anello (prende due anelli già realizzati e li collega grazie al terzo anello, una striscia di carta fissata con la cucitrice) È così bello che è stato scelto come logo dall’Unione Matematica Internazionale.
Dal pubblico si alza Alunn08:
Alunn08: Be’, se si vuole parlare di nodi nell’arte, direi che tocca a me… Anzi: tocca a Leonardo da Vinci! Forse può sembrarvi strano questo riferimento al genio di Leonardo in una conferenza sulla topologia, ma si tratta, appunto, di un genio e possiamo trovare qualche traccia di topologia anche nelle sue opere. La mostra che abbiamo presentato ai ragazzi durante il Festival è stata arricchita dalla cornice della biblioteca: con le finestre chiuse, in penombra o con l'illuminazione artificiale, abbiamo ricreato una bolla fuori dal tempo, sia per preservare i libri ivi conservati, sia per poter ricreare un percorso che si sviluppa attraverso i secoli.
Artista, inventore, scienziato… non è così facile definire Leonardo da Vinci, non possiamo incasellarlo o mettergli un’etichetta. Nato nel 1452, Leonardo fa il suo ingresso nella bottega di Andrea del Verrocchio da adolescente: il Verrocchio è un grande artista, ma anche un grande maestro, capace di insegnare ai propri allievi l’uso delle più diverse tecniche pittoriche dell’epoca. Secondo la leggenda, Verrocchio rimase così impressionato dal talento di Leonardo da rinunciare alla pittura per il resto della sua vita, sconfitto dal confronto con l'allievo.
Leonardo si definiva un “homo sanza lettere”: aveva un padre notaio, ma si era rifiutato di seguire le sue orme ed era stato il nonno probabilmente a trovargli il posto presso la bottega del Verrocchio. La sua curiosità insaziabile lo porta a studiare, tanto da costruirsi, nel corso della sua vita, una biblioteca importantissima. Lo sappiamo grazie ai suoi appunti, agli elenchi che abbiamo ritrovato sparsi tra i vari codici. Anche i suoi disegni degli animali sono il suo modo di capire il mondo, capire come si muovono, come sono fatti. Leonardo è un intreccio di scienza e arte: usa la scienza per esprimere meglio la sua arte, usa l’arte per capire la scienza.
Espressione dei suoi pensieri e dei suoi studi sono i suoi famosi codici: si tratta di disegni, schemi tecnici, annotazioni personali, battute di spirito, il tutto annotato con la sua scrittura speculare, orientata da destra a sinistra. Si tratta di migliaia di fogli di diverso formato e ne sono giunti fino a noi circa 8000, ovvero 1/3 di quanto ha realmente scritto. Leonardo avrebbe voluto riordinarli e classificarli, ma non riuscì mai. Alla sua morte li lasciò a Francesco Melzi, uno dei suoi allievi più cari, che li riportò a Milano nel 1523. Ma alla morte di Melzi, gli appunti furono in parte regalati, in parte venduti, in parte rubati.
A noi interessano dei particolari di questi codici: gli intrecci, i nodi vinciani! Sono intrecci che sembrano realizzati come scarabocchi per passare il tempo, gli stessi che tutti facciamo quando siamo annoiati, ma possono essere intrecci che costituiscono uno studio preparatorio per altre opere, oppure schemi per le sue famose macchine, oppure ancora decorazioni delle sue opere più famose (compare l’immagine della Dama con l’Ermellino, con l’ingrandimento di un particolare, un fregio del vestito che riporta, appunto, un intreccio). Tra le sue opere spiccano anche i labirinti, amati dai nobili, per i quali costituivano un passatempo.
Leonardo è vissuto a cavallo tra 1400 e 1500, mentre la nascita della topologia si attesta intorno al 1735, perciò lascerei la parola a Alunn09.
Alunn09: Grazie! Direi che è il momento di parlare della nascita della topologia, con l’opera di Eulero dedicata ai sette ponti di Konigsberg…
Al sentir nominare i ponti di Konigsberg, gli animatori di Grafo-mania presenti in sala salgono sul palco: Alunn10, Alunn11, Alunn03, Alunn12 e Alunn13
Alunn03: Se si parla di ponti di Konigsberg, le persone più adatte per parlarne siamo noi, visto che gestiamo il laboratorio di BergamoScienza dedicato a questa bellissima città. Dovete sapere che a Konigsberg ci sono sette ponti e, nella prima metà del 1700, gli abitanti, la domenica pomeriggio, amavano passeggiare su di essi, cercando un modo per passare su ogni ponte una volta sola, ma percorrendoli tutti. Per spiegarvi come fare, abbiamo deciso di rappresentare fisicamente la situazione. La città è divisa in quattro parti dal fiume Pregel e qui ci sono quattro animatori che possono rappresentarle e possiamo prendere questi nastri (sono stati predisposti dei nastri sul tavolo) per realizzare i ponti. Questi due (indicando Alunn12 e Alunn13) sono le due isole, mentre gli altri due sono le sponde del fiume. La prima isola è collegata ad ognuna delle sponde da due ponti (prende quattro nastri e li dispone in modo che colleghino l’isola alle rive), la seconda isola è collegata ad ogni sponda da un ponte (fa la stessa cosa con altri due nastri) e infine le due isole sono collegate tra loro da un ultimo ponte (ed ecco collocato l’ultimo nastro). Vediamo se c’è un volontario tra il pubblico per aiutarci con questa dimostrazione (sale sul palco Alunn14). Chiediamo a Alunn14 di attraversare tutti i ponti una sola volta: ogni volta che passerà sul ponte, lasceremo cadere il nastro corrispondente a mostrare che quel tratto di strada non si può ripercorrere.
Alunn14 fa un paio di tentativi, si chiama sul palco anche un altro elemento del pubblico (completamente ignaro) perché faccia il proprio tentativo, ma alla fine Alunn08 reagisce con impazienza:
Alunn08: Direi che il nostro pubblico ha capito benissimo come funziona. Se vogliono sapere qual è la soluzione, non hanno altra scelta che partecipare ai laboratori: a proposito, domenica pomeriggio avete l’ultima occasione per farlo. I laboratori si svolgono a scuola dalle 14.00 alle 17.30. Vi aspettiamo! (dopodiché fa cenno ad Alunn09 perché riprenda da dove è stato interrotto)
Alunn09: Grazie! Prima di essere interrotta, stavo dicendo che la nascita della topologia è evidenziata dall’opera di Eulero…
Prof4: (lanciandosi sul palco!) Ora, parlando di Eulero, non si può certamente tralasciare di citare la caratteristica di Eulero di uno spazio topologico! Ho giusto preparato delle slide per l’occasione... (la Prof5 lo interrompe subito)
Prof5: Sì, però cerchiamo di renderla un po’ più semplice di prima, che ne dici? Ti va di aiutarmi?
Prof4: Intendi con un esercizio pratico?
Prof5: Esattamente! Quando si parla di risultati matematici, spesso quelli più notevoli ci svelano regolarità inaspettate della realtà: uno di questi è indubbiamente la relazione di Eulero per i poliedri. Per farvi sperimentare quanto diciamo in maniera diretta, ora vi distribuiamo alcuni poliedri, che, come vedete, sono di vari tipi, e vi invitiamo, collaborando anche con i vicini, a fare questo semplice conteggio: contate il numero dei vertici del poliedro, sottraete il numero degli spigoli (lati), e sommate il numero delle facce... (alcuni alunni presenti prendono dei poliedri realizzati con il Polydron e li distribuiscono tra i presenti)
Pare proprio che si ottenga sempre 2.
Alunn05: (protestando vivacemente) Assolutamente no! Il mio ha dato come risultato zero!
Prof5: (lanciando uno sguardo di conferma a Prof4): Hai ragione! Ma tu non hai in mano un poliedro qualsiasi. Portalo qui! (Alunn05 sale sul palco, portando con sé un “poliedro toroidale”) Come vedete questo è diverso dai poliedri precedenti (nel frattempo mostra al pubblico in una mano il poliedro toroidale e nell’altra un cubo e un tetraedro). Perché è diverso dagli altri due?
Alunn05: (con entusiasmo) Perché è giallo!
Prof5: (infastidito): Direi che il colore non è così significativo. Qual è la differenza? Pensateci bene!
Alunn05: (dopo averci riflettuto un po’) Ha un buco!
Prof5: Proprio così: in effetti, si potrebbe dimostrare che il calcolo “vertici – spigoli + facce” della relazione di Eulero è influenzato dalla presenza di buchi. Sorprendente, no? Ora direi che possiamo lasciare di nuovo la parola a Alunn09 (invita Alunn09 a riprendere posto sul palco)
Alunn09: Grazie! (timidamente. E poi, rivolgendosi al pubblico) Eccoci ri-ritrovati! Direi che possiamo andare avanti con il nostro percorso, allora. L’ultima protagonista della nostra mostra è Maryam Mirzakhani. Nata a Teheran nel 1977, Maryam, fin da piccola, amava inventare storie e immaginava ragazzine che compivano grandi imprese. Leggeva parecchio, ma pare non amasse molto la matematica, e non mostrava di possedere un talento particolare. La sua insegnante di matematica del primo anno non vede in lei alcun talento e Maryam si convince di non essere molto brava. La prima persona che riesce a far nascere in Maryam l’interesse per la matematica è il fratello maggiore, che le racconta la storia di Friedrich Gauss e della formula per sommare i numeri naturali. Maryam comincia a intuire che la matematica potrebbe essere più interessante di quanto le era parsa fino a quel momento. A undici anni, conosce Roya Beheshti Zavareh, che ora è docente di matematica alla Washington University. Compagne di classe anche alle superiori, sentono parlare delle Olimpiadi internazionali di Informatica e decidono di partecipare, ma devono chiedere l'intervento della Preside del loro istituto, perché le competizioni sono chiuse alle donne. La prima partecipazione è nel 1994 a Hong Kong, dove Maryam vince la medaglia d’oro con un punteggio di 40 su 42, mentre nel 1995, in Canada, ottiene uno strabiliante punteggio pieno di 42 su 42. A quanto dice, la partecipazione alle Olimpiadi le ha mostrato la bellezza della matematica. Prova forti emozioni, e se in un primo momento la considerava una sfida, poi comincia a divertirsi e le piace l’opportunità che le viene data di pensare ai problemi di matematica. La bravura acquisita le apre le porte di Harvard, dove si ritrova Curtis McMullen come advisor, uno dei matematici più importanti del mondo. Conclude il dottorato nel 2004 e con la sua tesi dimostra una congettura aperta da anni. Nel 2008 si sposa con Jan Vondrak, e nel 2011 dà alla luce Anahita. Nel 2009 approda a Stanford e comincia la sua collaborazione con Alex Eskin, dell'Università di Chicago. La loro collaborazione li porta a raggiungere vette inesplorate, ma li obbliga anche a confrontarsi con le difficoltà: per due anni spendono lavoro e fatica e, nonostante la carenza di progressi, Maryam si mantiene positiva, grazie alla sua stabilità mentale e alla fiducia in sé stessa. Per raggiungere la cima, Maryam e Alex sono dovuti tornare al punto di partenza e, con pazienza, sperimentare un nuovo approccio per concludere il percorso. [7] Della matematica di Maryam, però, non sono in grado di parlare e ci dirà qualcosa la Prof2, alla quale cedo la parola prima che mi interrompa!
Prof2: Maryam è appassionata alla matematica delle superfici: qual è la distanza minore tra due punti? Sappiamo che nel piano è una linea retta. Su una sfera, è un arco della circonferenza massima. E su una ciambella? O su una ciambella con molti buchi? Nessuno conosceva le risposte. Se cammino in linea retta su una sfera, torno al punto di partenza. E anche su quello che i matematici chiamano un toro (e il resto del mondo chiama ciambella), se scelgo adeguatamente il mio percorso, posso tornare al punto di partenza. Ma potrei anche trovare un cammino infinito, che continua senza mai incontrare di nuovo sé stesso. Ce ne sono tanti che soddisfano questa caratteristica e sono tutti diversi tra loro: immaginiamo una formichina che si muove sulla superficie di questo salvag… ehm, toro! (presenta il percorso usando un salvagente e un nastro colorato, che viene avvolto attorno al toro) Potrebbe continuare all’infinito senza mai tornare al punto di partenza. Maryam non ha paura di mettersi alla prova per trovare una risposta e con Alex Eskin riesce a dimostrare il teorema noto come “Teorema della bacchetta magica”, perché risolve problemi che gli scienziati stavano affrontando da anni. Porta un cambiamento poderoso, nella matematica e non solo. Grazie ad esso, gli astronauti possono programmare percorsi più sicuri per le loro astronavi, i meteorologi possono predire il tempo più velocemente e con maggiore accuratezza, i ricercatori possono capire come si diffonde un’epidemia. Sono stati sufficientemente chiara Alunn09?
Alunn09: Sì, grazie! Maryam è stata la prima donna ad essere insignita della Medaglia Fields, nel 2014, e quando ha ricevuto la mail da parte della presidentessa dell’Unione Matematica, che la informava del conferimento del premio, Maryam, pensando si trattasse di uno scherzo, ha eliminato il messaggio.
Purtroppo, quando le è stato conferito il premio, Maryam era già sofferente per un cancro al seno ed è mancata nel 2017, a soli quarant’anni. La sua opera le è sopravvissuta ed è stato grande il segno che ha lasciato nella matematica.
Penso che sia ora di chiudere questo nostro percorso che è stato storico, artistico, matematico e costellato di leggende e teoremi strani. Forse siamo riusciti a convincervi che la topologia non è così male. Prof1, che dice? Le piace un po’ di più ora?
Prof1: Direi che mi avete convinta! Potrei persino pensare di realizzarci un’edizione di BergamoScienza!
Alunn07 (correndo verso il palco): c’è un’ultima cosa… [8]
Realizzato con il contributo di Carolina Bergamini, Chiara Bertoni, Luca Campagnoni, Asia Corna, Francesco Mognetti, e dei ragazzi che hanno partecipato ai laboratori di Topo-Scienza realizzati presso il nostro istituto, per partecipare al festival di BergamoScienza. L’articolo è la trascrizione (quasi) fedele della conferenza presentata al pubblico mercoledì 11 ottobre, nella Sala degli Affreschi dell’Accademia Tadini. Grazie al curatore dott. Marco Albertario per l’ospitalità e per le idee, sparse qua e là, grazie alle quali è stata realizzata la mostra presentata nel corso del Festival.
In allegato le slide realizzate per l'occasione
Bibliografia:
[1] La realizzazione di una bottiglia di Klein a partire da due nastri di Mobius, con il filmato di Numberphile, nel quale Cliff Stoll, appassionato di bottiglie di Klein, mostra come si può realizzare: https://arbitrarilyclose.com/2020/04/17/mathartchallenge-day-33-mobius-strip-klein-bottle/
[2] I pantaloni topologici: https://youtu.be/dGi1ibYQWFk?si=pW2gPNnU6uej3vDz
[3] Il teorema della palla pelosa spiegato da Raffaella Mulas con la sua matematica danzante: https://youtu.be/Eeki_8Hvm5E?si=mo4DJ1XFOMLqOPCw
[4] Ben Orlin, Math with bad drawings – Illuminating the ideas that shape our reality, Black Dog & Leventhal Publishers, New York
[5] dall’articolo di Oggiscienza del 28 gennaio 2019, “Sbrogliare il DNA con la teoria dei nodi” di Luisa Alessio https://oggiscienza.it/2019/01/28/teoria-dei-nodi-dna/index.html
[6] dal blog Matetango di Annalisa Santi, la spiegazione dei nodi borromei: http://annalisasanti.blogspot.com/2018/10/dallo-stemma-dei-borromeo-alla-teoria.html#:~:text=Il%20%22nodo%20borromeo%22%20si%20presta,come%20Corpo%2C%20Mente%20e%20Psiche.
[7] video sulla vita di Maryam Mirzakhani realizzato in occasione di #peopleformath2023 https://youtu.be/euZ_vbHMHK4?si=gFH_08MaMby6jgZt
[8] Johann Sebastian Bach, Canone 1 a 2 https://youtu.be/Y0_DeHSTLHU?si=0j0YM-v_Mg_Mr68n
© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy





