Matematici di profilo
«Matematici di profilo» è stato pubblicato nel novembre del 2021 dalla Casa Editrice Sole24 ore e l’autore è Umberto Bottazzini, uno dei maggiori esperti internazionali nell’ambito della storia e dei fondamenti della matematica. Nel 2006 ha vinto il Premio Pitagora per la divulgazione matematica e nel 2015 l'Albert Leon Whiteman Prize, il riconoscimento per la storia della matematica bandito dall’American Mathematical Society, «per le sue numerose opere in Storia della Matematica, in particolare sulla nascita della Matematica moderna in Italia e sullo sviluppo dell'Analisi nel XIX e inizio XX secolo».
Le 48 brevi biografie di questo libro «provengono da articoli apparsi nel corso degli anni nelle pagine de Il Sole 24 Ore-Domenica»: riorganizzate in ordine cronologico, rielaborate e liberate dai «riferimenti occasionali alle circostanze che hanno motivato gli articoli originali», costituiscono una storia della matematica discreta, ovvero fatta da una successione di punti distinti (i matematici), uniti da incontri e circostanze. Come nel gioco dei puntini della Settimana Enigmistica, il lettore riesce a individuare il disegno finale solo procedendo nella lettura, e il quadro restituisce ai suoi occhi una storia della matematica in versione semplificata, ma ricca di dettagli. «Questo libro non si rivolge agli specialisti», dichiara Bottazzini in apertura e ha come obiettivo il superamento dell’«idea che i matematici siano esseri bizzarri e stravaganti». Tra le pagine ritroviamo «uomini e donne che vivono immersi nelle temperie del loro tempo, protagonisti nel corso dei secoli della grande avventura della matematica», che hanno dimostrato «di possedere straordinarie capacità di invenzione, immaginazione e fantasia». I profili contengono notizie biografiche scevre di dettagli, visto che, ad esempio, gli anni di nascita e di morte sono riportati in un elenco alla fine del libro: si tratta, soprattutto di biografie matematiche, che mostrano come la vita dei protagonisti sia intessuta di matematica e, al tempo stesso, come la storia della matematica sia ricca di vita. Ogni profilo inizia con un evento importante, quello che ha spinto l’autore a scegliere il matematico per questa rassegna, in cui spesso, il protagonista è un altro matematico, che, con la sua autorevolezza, mostra l’importanza del lavoro svolto. Come in un ritratto pittorico, Bottazzini, con sapienti pennellate di parole, condensa in poche righe il lavoro svolto, la sua importanza nel percorso storico, mentre i legami con i precedenti e i successivi ci permettono di cogliere come nessun matematico sia un’isola, e quanto quegli incontri siano stati determinanti per costruire il nuovo percorso. Ogni capitolo è dedicato a un matematico o a una matematica, solo occasionalmente a una coppia di matematici, che non possono essere separati perché troppo presenti l’uno nella vita dell’altro.
La rassegna non poteva che aprirsi con Pitagora e la dimostrazione matematica, Euclide, autore di «uno dei testi più influenti nell’intera storia dell’umanità», e Archimede, che ha legato il proprio nome alle basi della matematica. Con un salto di quattordici secoli, si arriva a Fibonacci, che porta in Europa la sapienza orientale, a Piero della Francesca, con il suo Trattato d’Abaco, a Luca Pacioli con la Summa, fino a Cardano, «una delle figure più straordinarie e controverse del Rinascimento», il cui nome non può essere separato da quello di Tartaglia. Galileo non poteva che essere tra i protagonisti, con il suo lavoro sull’infinito, le «“meraviglie”», le «“fantasticherie” e [i] paradossi», mentre Torricelli e Cavalieri arrivano nella parte finale del suo percorso. Cartesio apre la strada a una nuova matematica, mentre Fermat, «genio universale» e «matematico dilettante», con Pascal contribuisce alla nascita della probabilità. Leibniz e Newton condividono «la gloria dell’invenzione del calcolo infinitesimale», mentre i Bernoulli, oltre ai grandi contributi matematici, partecipano alla nascita di «uno dei più grandi matematici della storia», il prolifico Eulero. Maria Gaetana Agnesi ha lasciato un segno nella storia della matematica con le sue «Istituzioni analitiche ad uso della gioventù italiana» e con la sua versiera, mentre Girolamo Saccheri, nel voler liberare Euclide dai suoi nei, contribuirà alla nascita delle geometrie non euclidee. Lagrange, “nuovo Newton” per i contemporanei, è «uno dei più grandi matematici di sempre», mentre Laplace contribuisce a dare visibilità al teorema di Bayes; l’insegnamento di Cauchy «“era una nube oscura, illuminata talvolta da lampi di genio”», come scrive il contemporaneo Menabrea. Sophie Germain, seconda donna della rassegna, condivide il capitolo con Maryam Mirzakhani: entrambe eccezionali e vittime di una morte prematura, ma la vicenda della Germain, con la necessità di fingersi uomo per poter studiare matematica, non può che ricordare un romanzo. Abel e Galois sono accomunati dalla gioventù e dalla loro capacità di lasciare un segno indelebile nella matematica, contribuendo alla nascita di una nuova branca, l’uno con le funzioni ellittiche, l’altro con i gruppi. Gauss, Bolyai e Lobačevskij sono uniti dal quinto postulato di Euclide e dalla nascita delle geometrie non euclidee, mentre Riemann non poteva mancare nella rassegna, essendo stato «un grande matematico, senza dubbio il più profondo e geniale dell’epoca e tra i più grandi della storia». Dedekind, è stato una «sorgente inesauribile di idee e una fonte continua di ispirazione», Cantor ha legato il proprio nome all’infinito, e Boole «ha segnato la nascita della moderna logica matematica». Visto il periodo, Bottazzini dedica un intermezzo ai matematici del Risorgimento, citando in particolare Luigi Cremona, Enrico Betti e Francesco Brioschi, e procede poi con Sofya Kovalevski, che sentiva che il suo destino era «“servire la verità, cioè la scienza, e tracciare la strada per le donne perché ciò significa servire la giustizia”». Poincaré abbraccia con la sua opera «non solo la matematica ma i più diversi campi della fisica», tanto da essere stato candidato tre volte al Nobel, mentre Ricci Curbastro e Levi-Civita, forse meno noti, ci hanno regalato, secondo Einstein, «“un meraviglioso esempio di come la matematica ha fornito lo strumento teorico per una teoria della fisica”». La rassegna italiana procede con Volterra, «un gigante, che ha dominato il panorama della matematica e della scienza non solo italiana nei primi trent’anni del secolo scorso», Enriques, «uno dei maestri della “scuola italiana” di geometria algebrica», e Castelnuovo, che «ha imposto i geometri italiani sulla scena matematica internazionale». Ramanujan non può che essere ricordato insieme a Hardy, mentre Hilbert porta con sé i celebri ventitré problemi che hanno contribuito a dare forma alla matematica successiva. Brouwer parla di matematica “intuizionista”, mentre le lezioni di Emmy Noether «divennero un punto di riferimento per i giovani matematici in Germania e all’estero». Gödel ha ottenuto «fondamentali risultati che hanno segnato lo sviluppo della moderna logica matematica», von Neumann ha contribuito all’«organizzazione funzionale alla quale si ispirano ancora oggi le macchine», e Wiener ha imparato da Hardy che «“la matematica era non solo una materia che si poteva studiare ma anche discutere e vivere”». Il secondo intermezzo è dedicato alla matematica tra le due guerre, con la lungimiranza della fondazione Rockefeller che darà luogo a «un programma di emergenza per far fronte alla emigrazione degli scienziati ebrei». Durante e dopo la guerra, troviamo Turing, pioniere dell’Intelligenza Artificiale, e de Finetti, con la concezione soggettivistica della probabilità; De Giorgi è ricordato per il suo appassionato impegno civile e per aver dimostrato il diciannovesimo problema di Hilbert, contemporaneamente a Nash, vincitore, con Nirenberg, del Premio Abel nel 2015. L’anno dopo il premio è andato a Wiles, colui che ha dimostrato l’ultimo teorema di Fermat, e che è uno dei due matematici ancora viventi di questa rassegna. L’altro è Perel’man, legato a Poincaré per merito della topologia, protagonista dell’incomprensibile rifiuto della medaglia Fields e del premio del Clay Institute.
Ogni matematico di questa rassegna apre la strada al successivo e, al tempo stesso, deve la propria grandezza a chi l’ha preceduto.
Il libro è poco impegnativo, ma ricco di spunti e curiosità interessanti, e offre l’opportunità di sentire la vera voce dei matematici, viste le numerose citazioni.
Leggi dei gas marzo 2024
Verifica di fisica, classe terza liceo scientifico
Argomento: leggi dei gas ideali e teoria cinetica
Durata: 60 minuti
Ultima lezione a Gottinga
«Ultima lezione a Gottinga» è stato pubblicato nel 2009 da 001 Edizioni, ma ha fatto la sua comparsa l’anno precedente durante il Festival della Matematica, dove è stato esposto in versione gigante sui muri dell’Auditorium di Roma. L’autore è Davide Osenda, un informatico appassionato di acquerelli che, quando era studente universitario, si è ritrovato per la prima volta fra le mani il libro Gödel, Escher e Bach di Douglas Hofstadter. Lo ha trovato «disorganico, ipnotico e mirabile», ma questa incredibile opera ha generato in lui il desiderio di presentare in maniera diversa proprio il tema dell’infinito. È così che prende piede la scelta di realizzare questo fumetto ad acquerelli, e di ambientarlo a Gottinga nel corso della Seconda guerra mondiale, probabilmente nel 1933. Il protagonista della prima parte è il professor Fiz, che, presentendo probabilmente la fine della sua epoca, visto che sono cominciati i rastrellamenti nazisti, tiene la sua ultima lezione di matematica in università. È una lezione un po’ particolare, visto che il professore non ha un pubblico, o almeno così crede: infatti, nascosto tra i banchi, si trova Alkuin Winkler. I nomi dei due protagonisti sono davvero ben studiati: ci regalano un’immagine di serietà e leggerezza, e non posso non citare, al riguardo, quanto hanno scritto i Rudi Mathematici nella recensione comparsa nel numero 131 della loro rivista (dicembre 2009). Per quanto riguarda il prof. Fiz, scrivono: «si può certo immaginare che il nome discenda dalla facile assonanza con il sistema FZ, quello di Fraenkel Zermelo: un nome visceralmente matematico». Mentre «il suo ultimo e imprevisto discepolo è invece già commistione tra passato e futuro, tra numeri e America. Ha il nome di Alcuino, precursore della matematica medievale e ricreativa, e il cognome dell’attore che interpreta Fonzie. Perché la matematica sa essere spettacolo».
Alkuin assiste in silenzio a questa lezione e, quando il professore decide di allontanarsi, si palesa, chiedendo che l’argomento venga concluso: a quel punto la matematica non è più un monologo con la lavagna, ma un dialogo che coinvolge anche altri strumenti, come le carte da gioco. «Il mio tempo, ormai, è venuto.» dichiara il professore alla fine, prima di stringere la mano ad Alkuin, augurandogli una vita piena: «Se la sua passione per la matematica non appassirà, avrà tempo per approfondire queste discipline pure e lontane…» Mentre il professore si avvia in silenzio verso il suo triste destino, Alkuin si perde nel mondo colorato della matematica e, dopo essere stato accompagnato al confine dai partigiani, riesce a fuggire. Lo ritroviamo a Princeton nel 1963, l’anno di uscita della dimostrazione di Cohen, la parola finale all’ipotesi del continuo di Cantor.
Il racconto si snoda attraverso gli infiniti, partendo dall’inizio, visitando l’albergo infinito di Hilbert, mostrandoci il percorso di Cantor fino all’intervento di Gödel. La lezione è bellissima e particolarmente ispirata: mostra un docente alla ricerca delle parole giuste, delle metafore più illuminanti, dà l’idea di come i matematici riescano a perdersi nel proprio mondo anche quando attorno a loro il resto del mondo sta crollando. E la stessa cosa succede, in un secondo momento, ad Alkuin, che nel momento della sua fuga, quando è costretto ad una lunga attesa in una cascina abbandonata, trova rifugio nella matematica. L’immagine della matematica come rifugio e fuga dalle brutture del mondo è forse il dipinto più bello tra gli acquerelli proposti da Osenda.
Durante la lezione del professor Fiz, Osenda si serve di acquerelli particolarmente colorati per illustrare il mondo della matematica. Pur scrivendo su una lavagna nera, il professore crea un mondo nuovo ricco di colori e calore che conquista Alkuin, e fa da contraltare alla persecuzione nazista che è monocolore. Questo particolare grafico è sottolineato da Piergiorgio Odifreddi nella sua introduzione intitolata «Era una notte buia e tempestosa», dove parla di «chiaroscuro infernale del nazismo» contrapposto «alla luminosità paradisiaca della matematica». La notte buia è quella in cui il professore viene arrestato, la notte buia è quella che sta attraversando Gottinga, quella che viene raccontata da Odifreddi facendo riferimento alle amare parole di Hilbert: «Non c’è più nessuna matematica a Gottinga!». Richiamando la nostra attenzione sulla matematica, Odifreddi riconosce come le illustrazioni riescano «a far intravedere con gli occhi del corpo ciò che si può vedere compiutamente solo con gli occhi della mente: la complessità del problema del continuo». La benedizione matematica di Odifreddi è seguita dalla benedizione grafica di Andrea Plazzi, laureato in matematica, ma editor nel campo dei fumetti e noto per la sua consulenza per le opere di Leo Ortolani, autore di Rat-Man. Andrea Plazzi riparte dall’inizio, con il libro da cui ha avuto origine l’ispirazione di Davide Osenda: «Gottinga colpisce per il coraggio e la sicurezza con cui l’autore tratta – in e con un linguaggio visivo – temi e argomenti concettuali e intrinsecamente astratti, che non si prestano a facili visualizzazioni». Più avanti, sottolineando la padronanza mostrata da Osenda, Plazzi ricorda che questo fumetto «non è né un libro di divulgazione scientifica né un manuale illustrato; narra una storia e lo fa con umanità profonda, che accompagna sempre il lettore».
Da quanto leggiamo nelle due prefazioni, sembra che questo fumetto dovesse essere solo l’inizio di una lunga vicenda in tre parti, ma purtroppo non ha avuto seguito. Non solo: è difficile reperire questo testo, visto che non è disponibile nemmeno negli store online. Mi è stato possibile leggerlo solo grazie alla rete bibliotecaria.
Circonferenza febbraio 2024
Verifica di matematica, classe terza liceo scientifico
Argomento: circonferenza
Durata: 120 minuti
A Pisa con Galileo - A Cambridge con Newton
«A Pisa con Galileo» e «A Cambridge con Newton» sono stati pubblicati dalla Casa Editrice Dedalo a ottobre 2023, nella collana Scienza in viaggio, che «racconta le intuizioni e le scoperte dei più grandi scienziati attraverso un viaggio nei luoghi in cui hanno vissuto». L’autrice Silvia Merialdo è laureata in fisica nucleare e ha avuto esperienze di ricerca nel Regno Unito e in Germania; è redattrice di testi di fisica per la scuola presso la casa editrice Zanichelli, ma scrive anche guide turistiche, come quella dedicata a Genova, la sua città, e quella sul trekking sull’Appennino con i bambini, e con questo libro coniuga le due passioni, descrivendo luoghi turistici e spiegando scoperte scientifiche. Entrambi i libri sono arricchiti dalle illustrazioni di Gaia Aloisio ed Emanuela Carbonara, che hanno collaborato anche al libro Un viaggio nella relatività di Federico Benuzzi.
Protagonista dei due percorsi è Andrea, una ragazzina che, grazie alla zia Paola, insegnante all’Università di Pisa presso la facoltà di ingegneria aerospaziale, ha modo di esplorare nuovi luoghi: il primo viaggio, a Pisa, è fatto proprio per raggiungere la zia, mentre il secondo, a Cambridge, è effettuato per accompagnare la zia che deve tenere una serie di lezioni. In entrambi i casi, Andrea ha come compagni di viaggio dei coetanei: nel primo caso si tratta dell’appassionato di fotografia Luca, figlio di un amico dei genitori, e nel secondo caso è Ravi, dedito al canottaggio, figlio di un’amica della zia. I due libri hanno la stessa struttura: dedicati al pubblico dei bambini della primaria, sono un misto di scienza e turismo e le illustrazioni che accompagnano la narrazione hanno il compito di mostrare i luoghi descritti e gli esperimenti raccontati. Nel percorso si inseriscono anche alcuni esperimenti che i giovani lettori possono svolgere con l’aiuto di un adulto, mentre i termini più complessi vengono evidenziati in grassetto e raccolti in un piccolo glossario molto esaustivo.
Nel caso di Galileo Galilei, «Andrea scopre l’universo» (come recita il sottotitolo). Incontra Galilei sulla Torre di Pisa, in un momento di malessere causato dalle vertigini. Dopo la torre, Andrea e Galileo si incontrano di nuovo al Camposanto, dove vengono descritti il pendolo e la passione per la Divina Commedia, poi al Palazzo della Sapienza, dove si parla di caduta dei gravi, e alla Torre del Cantone, dove l’invenzione del telescopio domina la scena. Le vicende legate al processo non potevano che essere raccontate all’interno del Battistero, mentre il metodo scientifico viene descritto con un diagramma di flusso all’interno della Cittadella Galileiana, la «ludoteca scientifica dove si possono fare esperimenti».
Insieme a Newton, «Andrea scopre la gravità», dopo che una mela le è caduta in testa nel cortile dell’Università. Dalla legge di gravitazione universale, che porta al confronto tra la mela alla Luna, all’ottica con i pericolosi esperimenti dello scienziato, dall’arcobaleno e dai prismi, con due esperimenti dedicati all’ottica, fino ad arrivare al calcolo differenziale, che l’autrice riesce a descrivere con semplicità, grazie al celebre Ponte Matematico al Queen’s College, non manca nulla. Si parla anche dei difficili rapporti di Newton con i contemporanei, delle comete e delle maree, vengono spiegati sperimentalmente i tre principi della dinamica – al terzo viene dedicato anche un esperimento – e dopo aver parlato del lavoro alla Zecca, il percorso si chiude davanti al melo.
In entrambi i casi, i due scienziati vengono descritti a tutto tondo e non può non colpire il carattere litigioso e un po’ burbero di Newton. Semplici, ma completi, chiari e simpatici, i due racconti contribuiscono ad avvicinare alla scienza i giovani lettori, mentre le illustrazioni movimentano la narrazione e consentono di memorizzare meglio i singoli passaggi. La curiosità e l’impazienza della piccola Andrea rappresentano i piccoli lettori, che possono trovare, in questi due libri, un’occasione per imparare divertendosi.
Calcolo delle probabilità febbraio 2024
Verifica di matematica, classe seconda liceo scientifico, recupero per assenti
Argomento: calcolo delle probabilità
Durata: 60 minuti
218 - 18 febbraio 2024
Carnevale della matematica
Il Carnevale della matematica di febbraio, il numero 175, è stato ospitato dai Rudi Matematici sul Blog di Le Scienze. Lo stile è davvero inconfondibile e il tema, “La matematica dei numeri tondi, o arrotondata, o degli anniversari”, non è stato scelto a caso: in questo mese, infatti, i Rudi Matematici celebrano due numeri tondi, 25 e 300 (che sono più che mai presenti a mo’ di messaggio subliminale nelle immagini del post), che rappresentano i 25 anni della più celebre e-zine della rete e il 300° numero appena uscito. Ricevo la celebre rivista, «fondata nell’altro millennio», da quando ho cominciato a bazzicare internet (diciamo che la ricevo da almeno vent’anni) e ogni volta che ricevo la mail che mi avvisa dell’uscita, mi ritrovo a sorridere grazie allo stile elegante con cui viene raccontata qualsiasi cosa. Dovete provare a leggere questo carnevale per capire cosa intendo, così scoprirete anche che, visto che i contributi vengono presentati in ordine di ricezione, per una volta non sono finita ultima. Il mio contributo è arrivato una manciata di ore prima della scadenza, perché ho concesso tempi più lunghi del dovuto ai miei alunni di terza per completare l’analisi dei questionari pervenuti per l’indagine statistica riguardante la presenza della matematica nel mondo del lavoro. Oltre a voler sapere quanto sia presente la matematica nei singoli lavori, obiettivo dell’indagine era quello di indagare i sentimenti nei confronti della matematica e di capire se il percorso scolastico fornisca buone basi per affrontare il mondo del lavoro. Dopo aver definito gli obiettivi, predisposto il questionario, diffuso il link per la compilazione, i ragazzi hanno analizzato i questionari raccolti in un file Excel, lavorando in piccoli gruppi e hanno poi presentato i propri risultati al resto della classe, in un lavoro che non è stato conteggiato solo per educazione civica, ma anche come orientamento al mondo del lavoro. Dal punto di vista didattico, l’esperienza ha avuto un grandissimo valore, visto che i ragazzi si sono trovati vittime di alcuni bias cognitivi, hanno dovuto imparare a confrontarsi e collaborare, e hanno capito che se si lascia il comando ad Excel, ci si potrebbe ritrovare grafici che dicono il contrario di ciò che affermano i dati raccolti. È capitato, infatti, che qualcuno travisasse il risultato proprio per colpa del grafico scelto, sicuramente piacevole esteticamente, ma poco chiaro quando si trattava di farne una lettura adeguata. Nell’analisi dei dati sono state notate alcune incongruenze: in alcuni casi, pur svolgendo la stessa identica professione, è stato segnalato un uso diverso della matematica: a seconda della formazione della persona in questione (ad esempio: al livello dirigenziale si può accedere sia con una laurea scientifica che con una laurea non scientifica) è stata riconosciuta una presenza o un’assenza di matematica. In altre parole, parafrasando una celebre citazione: la matematica è negli occhi di chi guarda.
Educazione civica
Ho cominciato a trattare il calcolo delle probabilità in seconda a gennaio, sovrapponendolo in questo modo alle ultime fasi del capitolo dedicato ai radicali. Avendo svolto il grosso del lavoro sui radicali prima delle vacanze di Natale, gennaio è diventato un modo per ripassare le operazioni con i radicali e gli strumenti dell’algebra di primo grado acquisiti nell’anno precedente e dove i radicali sono presenti come coefficienti. Questa ultima parte sui radicali, per quanto irrinunciabile, viene in genere percepita come noiosa, perciò ho deciso di presentarla in un modo un po’ originale, e di gestire il recupero attraverso giochi cooperativi, lasciando poi spazio a un paio d’ore a settimana al calcolo delle probabilità. Oltre al calcolo vero e proprio, l’argomento viene usato come tema di educazione civica, visto che viene affrontata, in primis, l’azzardopatia, e poi si vede l’applicazione nelle aule di tribunale, nelle scelte in ambito medico e nelle decisioni che ogni giorno compiamo in condizioni di incertezza. Il lavoro è stato arricchito dai contenuti delle letture di cui ho parlato nelle ultime newsletter, come Fate il nostro gioco di Diego Rizzuto e Paolo Canova, La legge del perdente di Federico Benuzzi, il Teorema di Bayes scritto da Roberto Natalini per la collana di Le Scienze, e Calcolo delle probabilità del prof. Francesco Daddi, che offre un’ampissima casistica di esercizi già svolti, rivelandosi un ottimo strumento per gli insegnanti, oltre che per gli studenti.
Anche in terza ci sarà modo di affrontare l’educazione civica, grazie alla termodinamica. Per ora, avendo cominciato la teoria cinetica dei gas e avendo fatto riferimento alla celebre curva di Gauss, ho proposto agli studenti la descrizione della curva effettuata da Federico Benuzzi, con il video Gaussiana, tra culturisti e clima. Federico ha la capacità di spiegare le cose con leggerezza, e di offrire, quindi, l’occasione per un momento di evasione.
Nuova Lettera Matematica
È uscito il quarto numero della Nuova Lettera Matematica e nel suo editoriale Renato Betti parla di curiosità come molla per raggiungere la conoscenza, introducendoci al tema della rivista, che contiene un mix di didattica e contenuti disciplinari. Gli articoli sono ricchi di illustrazioni e corredati da un’ampia bibliografia, e il numero si chiude con la nuova rubrica dei Rudi matematici e con alcuni suggerimenti di lettura. L’articolo che mi ha colpito in particolare è quello dedicato al progetto spagnolo Innovamat, che viene presentato da Albert Vilalta Riera, professore della Facoltà di Scienze dell’educazione della Universitat Autonoma de Barcelona, che esordisce ricordandoci come la matematica venga spesso percepita «come un ramo della conoscenza freddo, astratto e difficile, praticamente inaccessibile eccetto a pochi privilegiati», tanto da causare spesso una “ansia da matematica”. Secondo quanto leggiamo nell’articolo, «I problemi sono per l’attività matematica come le montagne per l’alpinismo […] Una sfida in attesa di essere superata». Il decalogo proposto può offrire numerosi spunti, visto che esordisce con una esortazione ad amare la matematica e prosegue invitando a proporre «attività di suolo basso, tetto alto e pareti grandi», dove il suolo basso indica che «non ci sono barriere in ingresso», il tetto alto permette di volare in alto e le pareti grandi suggeriscono che «non c’è un’unica strada stretta per risolvere il problema». L’ultimo comandamento suggerisce di fare «in modo che tutte le allieve e gli allievi abbiano i loro momenti di gloria matematica», perché «dobbiamo tenere sempre presente che, con le nostre decisioni, condizioniamo questi momenti di gioia». In altre parole, facciamo in modo di diffondere l’amore per la matematica.
Matematica benaugurale
In occasione della cerimonia di inaugurazione dell’anno accademico dell’Università degli Studi di Bari Aldo Moro, martedì 6 febbraio Sandra Lucente ha tenuto un intervento, seguendo il tema del “senso del limite”. È possibile leggere il suo intervento, riportato su MaddMaths!, o ascoltarla direttamente su YouTube, gustandosi fino in fondo il suo modo di presentare una matematica che si esprime attraverso gli oggetti. Il racconto si snoda attraverso i secoli, fino ad arrivare ai giorni nostri e contiene un po’ l’eco del racconto in forma di dialogo presentato in Quanti? Tanti!, il suo ultimo libro. Infatti, il percorso si apre con Euclide, per passare poi ad Aristotele, fare un salto fino a Galileo Galilei e raggiungere infine Georg Cantor, nel tentativo di confrontare e di misurare per comprendere. La partenza è con la frase di Euclide «l’intero è maggiore della parte», mentre Aristotele dice che «il tutto è maggiore della somma delle parti», Galileo Galilei va oltre dicendo che «c’è un tutto non maggiore della sua parte», mentre Georg Cantor conclude con «negli insiemi infiniti l’intero è equipotente ad una sua parte propria»: con i suoi discorsi sull’infinito, Cantor scompagina le carte, ma al tempo stesso ci regala un nuovo paradiso. Con l’ingresso nel Novecento «persino i matematici hanno imparato a rispondere alle domande con la parola “dipende”», che ritroviamo nelle geometrie non euclidee e nella topologia, mentre anche Calvino sembra schierarsi dalla parte di Aristotele quando in una lettera d’amore alla moglie scrive «“io credo che noi due a e b se siamo insieme non valiamo solo la somma a+b ma una quantità maggiore di a+b”». La conclusione è che «Ogni parte è essenziale per l’intero» e viene scandito più volte, nell’ultima parte del discorso, perché sia chiaro, perché si sedimenti dentro l’ascoltatore, perché «è il paradigma con cui dovremmo vivere questo nuovo tempo» e succede esattamente come nel segmento: se togliamo uno degli infiniti punti, non abbiamo più un segmento!
Tornando a Euclide
Abitando a 40 km di distanza dalla scuola in cui insegno, passo una frazione importante della mia giornata in auto. Ho imparato ad arricchire questi momenti con l’audiolettura dei classici. Ho ripreso in mano I pilastri della Terra di Ken Follett, letto quasi una trentina di anni fa e vi ho ritrovato, con stupore, Euclide. Uno dei protagonisti dice di aver scoperto Euclide e, per quanto uno dei suoi interlocutori riconosca che «Un uomo guadagna sempre se comprende qualcosa!», lui si trova in difficoltà nel tentativo di far capire l’importanza di quanto ha appreso: «Ora che capisco i principi della geometria posso trovare soluzioni per problemi nuovi che sconcertavano il mio patrigno». Ciò che lo sconcerta di più è il metodo di Euclide, che, a partire dai cinque assiomi, «deduce tutto il resto per mezzo della logica».
Elogio della matematica
L’elogio della matematica di Enrico Bucci, comparso su Il foglio il 29 gennaio scorso, è il naturale proseguimento di una riflessione scaturita da un confronto sui social, in seguito alla condivisione del lavoro fatto dai miei alunni sull’indagine statistica. Per necessità di sintesi, sui social ho condiviso solo l’incipit dell’articolo, nel quale era presente la frase del medico dal quale è scaturita, poi, la mia idea di svolgere un’indagine statistica. Uno dei miei contatti ha ribadito in un commento che davvero la matematica non serve a nulla, ma, ha proseguito: «potrebbe servirti per essere libero di scegliere che vita fare in futuro». Si tratta del collega che gestisce il profilo @uselessmaths, che porta già nella scelta del nome la sua convinzione. Enrico Bucci parte dalla stessa base e conclude ribadendo un passaggio importante e cioè che per motivare davvero gli alunni, dovremmo disabituarli «al perenne suono della domanda “a che serve”, per educarli invece a quello della domanda “perché”». L’importanza della matematica si esprime nel fatto che è il linguaggio con il quale si esprime la nostra mente ed è l’unico modo per condividere senza rischiare ambiguità: «La conoscenza della matematica è direttamente proporzionale alla nostra capacità di formulare, esaminare e comunicare questa forma di pensiero di cui costituisce il linguaggio più appropriato».
Per concludere, ricordo che: «Ogni anno, in occasione di questa giornata, l’IMU organizza un concorso interattivo aperto a tutti, e per il 2024 si tratterà della Math Remix – 2024 creative challenge, una sfida atta a vedere la matematica nel nostro ordinario, a riconoscere schemi in quello che vediamo tutti i giorni e immortalarli in un’istantanea.» C’è tempo fino al 4 marzo e tutte le informazioni si possono trovare sul sito di MaddMaths!
Buona matematica e buon cammino! Ci sentiamo tra TRE settimane!
Daniela
PS: Traduzione della vignetta: “Ok, Calvin, controlliamo i tuoi compiti di matematica.” “Non facciamolo e diciamo di averlo fatto.” “La tua insegnante dice che hai bisogno di spendere più tempo sugli esercizi. Siediti.” “Più tempo?! Ho già speso dieci interi minuti! Dieci minuti! Sprecati! Giù per lo scarico!” “Qui hai scritto 8+4=7. Lo sai che non è giusto.” “E va bene, ho sbagliato di un po’. Fammi causa.” “Non puoi aggiungere cose e ritrovarti con meno di quello che avevi in partenza!” “Certo che posso! È un paese libero! Ho i miei diritti!”
Probabilità ed educazione civica
Il calcolo delle probabilità è parte integrante del programma di matematica del liceo scientifico: dopo un primo approccio in seconda, con un cenno al Teorema di Bayes, si procede, in quarta, con un approfondimento, grazie ai nuovi strumenti offerti dal calcolo combinatorio e ad una maggiore capacità di astrazione.
Il calcolo delle probabilità è anche estremamente utile per affrontare un percorso di educazione civica e il collegamento più immediato ha a che fare con l’azzardopatia, anche se, in generale, la probabilità ci offre un modo di interpretare la realtà, entrando nelle aule di tribunale, negli ospedali e nelle decisioni che prendiamo ogni giorno.
Ho cominciato il percorso con i miei alunni di seconda sfruttando il lavoro di Taxi1729, una società di consulenza, formazione e comunicazione scientifica, il cui lavoro, come recita l’homepage, ha «un unico filo conduttore: la decisione umana». Il primo video, Gratta e vinci: compulsivi per legge, mostra fin da subito che ci sono studio e pianificazione dietro la forza del gioco d’azzardo.

«Nel 1997, in una relazione alla Camera dei deputati sull’andamento dei Gratta e Vinci, il Ministro delle Finanze Visco si dichiara soddisfatto degli ultimi incassi ottenuti per lo Stato e fa una lista dei punti di forza di questo gioco, su cui investire negli anni successivi». I punti di forza sono l’intimità, data dal sentirsi protagonista del gioco, l’illusione della vincita, perché come lascia capire la pubblicità è facile vincere, le piccole vincite, visto che un biglietto su quattro è vincente, e le quasi vincite, che generano frustrazione, ma fanno anche venir voglia di riprovarci subito. Anche i mass media sono complici di questi incassi dello Stato, perché ogni volta che c’è una grande vincita, questa viene enfatizzata, invogliando gli spettatori a diventare giocatori, a tentare la fortuna. Anche se siamo consapevoli che le probabilità di vincita sono molto basse, il fatto che qualcuno vinca ogni tanto ci porta a illuderci di poter essere, un giorno, uno dei fortunati vincitori.

Insegno a Lovere, sul Lago d’Iseo, e sono a pochi minuti di auto da Rovetta (in provincia di Bergamo) dove «è stato centrato il 6 dei record al SuperEnalotto!» il 16 febbraio del 2023. Il giorno dopo, Paolo Canova e Diego Rizzuto di Taxi1729 hanno pubblicato il video Qui vinti 371 milioni di euro! proprio per parlare della vincita. Quando ho fatto il percorso con la seconda dell’anno scorso, la vincita è stata realizzata proprio il giorno che i miei alunni affrontavano la verifica scritta sull’argomento e il giorno della consegna ho mostrato il video. Come ricorda Diego verso la fine, quel 16 febbraio ha coinciso con «il 21° Bradbury day, ovvero il ventunesimo anniversario (a proposito di improbabilità) della improbabilissima vittoria olimpica del pattinatore australiano Steven Bradbury», vincitore della prima medaglia d’oro australiana alle Olimpiadi invernali.

La vittoria è stata così inaspettata per tutti che “doing a Bradbury” in Australia è diventato un modo di dire che indica «un successo clamoroso e altamente insperato». Allo stesso livello si pone quanto successo a Randy Johnson, che ha colpito un colombo lanciando una palla durante una partita di baseball, il 24 marzo 2001. Anche questo evento è altamente improbabile, e consapevolmente Randy ha usato l’unicità di quanto successo per farne il suo logo, ora che esercita la professione di fotografo.
Nel percorso sulla probabilità è per me estremamente importante sottolineare come il nostro intuito non sempre ci aiuti ad affrontare le situazioni: spesso ci porta fuori strada, spingendoci a valutare erroneamente la probabilità di un evento. Ho continuato il percorso, quindi, parlando del paradosso di Monty Hall, che poi non è altro che un’applicazione del teorema di Bayes. Ho cominciato con un piccolo estratto del film 21, nel momento in cui il professore Mickey Rosa capisce che l’allievo del MIT Ben Campbell potrebbe essere un ottimo acquisto per la squadra che sta addestrando a vincere ai tavoli del Blackjack. Il professore offre a Ben «l’occasione di beccarsi un credito extra», parlando di quello che lui chiama «il problema del conduttore di quiz televisivo»: «Ben, diciamo che stai giocando in televisione e hai la possibilità di scegliere fra tre porte diverse, intesi? Dunque: dietro una delle porte c’è un’auto nuova, dietro le altre due: capre!» Sul sito Mathigon si può procedere con una simulazione del gioco e io lo faccio in classe, offrendo alla classe anche l’occasione di ripassare un po’ l’inglese. Una volta che è stata effettuata la scelta, il presentatore apre una delle porte non scelte e dietro la quale c’è, ovviamente, una capra. A questo punto del gioco, è più conveniente tenere la prima scelta o cambiare porta? Ben non ha dubbi e dà la risposta giusta, ma a me piace procedere leggendo la descrizione che ne fa Christopher, il protagonista del libro di Mark Haddon Lo strano caso del cane ucciso a mezzanotte, perché offre anche l’occasione di riflettere su come funzioni la matematica: «Il signor Jeavons disse che mi piaceva la matematica perché mi faceva sentire al sicuro. Disse che mi piaceva perché la matematica serve a risolvere i problemi, poi aggiunse che questi problemi erano difficili e interessanti, ma che alla fine c’era sempre una risposta chiara e diretta per tutto. Ciò che intendeva era che la matematica non è come la vita perché nella vita non esistono risposte chiare e dirette. So che era questo che voleva dire perché è quello che ha detto. Perché il signor Jeavons non capisce i numeri». Per questo motivo, il capitolo 101 del libro (ovvero il 26°) è dedicato al paradosso di Monty Hall, che viene esplorato nel dettaglio, insieme alla vicenda di Marilyn vos Savant, che aveva spiegato il problema dalle pagine della rivista americana «Parade». La sua risposta giusta le è costata un forte attacco, visto che molti scrissero alla rivista contestando la sua risposta: «Il 92% delle lettere sostenevano che si era sbagliata, e molte provenivano da matematici e scienziati». Roberto Natalini, dalle pagine del libro Teorema di Bayes, ci ricorda che «persino il famoso matematico Paul Erdős pensava inizialmente che la soluzione proposta da Selvin e vos Savant fosse sbagliata» (Steve Selvin è lo statistico che risolse il problema per la prima volta nel 1975, e il fatto che lui non sia stato attaccato pesantemente come la vos Savant mi spinge a pensare che parte dell’attacco sia imputabile a una questione di genere).

Per continuare a lavorare sui bias cognitivi legati alla probabilità, chiedo ai miei alunni di mettersi in gioco con il test proposto da Paolo Canova e Diego Rizzuto nel libro Fate il nostro gioco: ci sono 10 eventi diversi e gli alunni devono metterli in ordine, dal più probabile al meno probabile. Non è certo facile procedere senza calcoli e senza ricerche in rete, usando solo l’intuito: «Nei numerosi incontri che abbiamo fatto in giro per l’Italia, nessuno ha mai indovinato l’ordine giusto. Un po’ perché di alcune di queste cose sappiamo poco o niente, dunque facciamo fatica a stabilirne la probabilità, un po’ perché è molto difficile sottrarsi all’influenza delle speranze, delle paure, delle esperienze passate, dell’amplificazione mediatica o al nostro naturale istinto di accordarci alle opinioni altrui», dichiarano i due autori.
Parlando di nuovo del SuperEnalotto, non posso non dare ascolto ad un’altra voce autorevole nel campo dell’azzardopatia, Federico Benuzzi, docente, giocoliere, attore, autore del libro La legge del perdente e autore e protagonista dello spettacolo teatrale L’azzardo del giocoliere, di cui il video A cosa serve la matematica? Il SuperEnalotto non è che un estratto.

In modo molto coinvolgente, Federico Benuzzi descrive la vittoria al SuperEnalotto come la scelta di una carta, precedentemente firmata, in un mazzo con 600 milioni abbondanti di carte. Immaginando di mettere in fila tutte le carte, in un serpentone di 311 km, che si snoda da Bologna al casinò di Locarno, «camminate accanto al mazzo e quando finalmente siete paghi, vi fermate, vi chinate, ne pescate una e se è quella che avete scelto avete vinto 130 milioni di euro». Nonostante l’improbabilità che questo avvenga, «il fatturato del gioco d’azzardo, in Italia, è circa 90 miliardi l’anno! Quasi l’8% del PIL! […] Si stima che gli italiani spendano, in gioco d’azzardo, il 10% di quello che spendono come privati!»
In questa passeggiata tra le probabilità, mi piace fare riferimento a storie che in qualche modo possano restare impresse e che aiutino, quindi, a collocare meglio quanto dico dal punto di vista matematico. Per questo motivo, non può mancare Roy Sullivan, del quale ho sentito parlare per la prima volta quando ho visto online la conferenza di Paolo Canova e Diego Rizzuto al Salone del libro nel 2013. L’ho ritrovato, ovviamente, anche tra le pagine del loro libro, nel capitolo dedicato agli eventi improbabili, come «manifestazione empirica che l’improbabilità esiste e vive insieme a noi».

Roy Sullivan è un guardiaparco, che, nell’arco della sua vita, è stato colpito sette volte da un fulmine, a dimostrazione del fatto che anche ciò che indichiamo come «praticamente impossibile» potrebbe verificarsi. Nel corso della conferenza, la vicenda di Roy Sullivan è presentata per rispondere all’obiezione di chi potrebbe riconoscere che per quanto la vittoria al SuperEnalotto sia «praticamente impossibile», è fuor di dubbio che qualcuno, ogni tanto, vince! Diego e Paolo citano la legge dei numeri grandi, per sottolineare che anche se la probabilità di vincere, per il singolo, è molto bassa, quando ci sono molte persone che giocano, la probabilità che, all’interno della popolazione, qualcuno vinca potrebbe essere anche molto alta. In altre parole, se in un gruppo di cinque persone lanciamo un dado a sei facce e ognuno di noi scommette su una faccia diversa, la probabilità che qualcuno di noi riesca a vincere è molto alta (5/6), mentre la probabilità del singolo non è cambiata (1/6).
Torno poi alle fasi iniziali della conferenza e lascio che Diego e Paolo raccontino l’incredibile vicenda del processo di O.J. Simpson, ripresa anche da Paolo Caressa in un articolo pubblicato su Prisma, La probabilità condizionata del Reverendo. La vicenda è quella del processo che ha fermato gli USA quando, il 3 ottobre 1995, stava per essere emanato il verdetto: O.J. Simpson era accusato di aver ucciso la ex moglie, Nicole Brown Simpson, ma alla fine del processo verrà giudicato “Not guilty!”, non colpevole. L’accusa aveva dimostrato la presenza di violenze domestiche durante il loro matrimonio, sposando la tesi secondo la quale, essendo un uomo violento, era molto probabile che fosse lui il responsabile della morte della ex moglie. La difesa, gestita dal cosiddetto Dream Team, ovvero il gruppo di avvocati migliore sulla piazza, aveva quindi proceduto con il calcolo delle probabilità, studiando le cifre dell’anno precedente: su 4 milioni di donne picchiate dal partner, “solo” 1600 erano state uccise, ovvero lo 0,04%, quindi era estremamente improbabile che O.J. Simpson fosse il responsabile della morte della ex moglie. Un dream team per l’accusa, con almeno un matematico, avrebbe forse potuto ribaltare il verdetto: c’è un errore macroscopico alla base del ragionamento, perché l’insieme di riferimento, ovvero l’insieme dei casi possibili, non può essere quello delle donne picchiate dal partner. Alla luce di quanto successo, l’insieme di riferimento deve essere quello delle donne che hanno subito violenza domestica E che sono state uccise. A questo punto, con questo nuovo insieme al denominatore costituito da 1800 donne, la probabilità diventa 1600/1800, ovvero dell’89%. Il Reverendo Bayes avrebbe potuto aiutare gli avvocati a fare realmente giustizia.

In classe, è stato necessario anche dedicare un po’ di tempo al calcolo, esplorando la teoria della probabilità attraverso alcuni esercizi, per capire ancora meglio i problemi che ci eravamo posti. Ho usato il libro del prof. Daddi Calcolo delle probabilità come supporto, ma ho avuto modo di utilizzare anche gli esempi proposti da Roberto Natalini nel suo libro Teorema di Bayes, pubblicato nella Collana di Le Scienze. Ci siamo divertiti con Il problema dei gattini, dove «una gatta ha partorito due gattini di cui almeno uno è maschio. Qual è la probabilità che anche l’altro sia maschio»?, che è indicato come un paradosso. Poi non ho potuto non parlare del problema dei test diagnostici e, seguendo le orme di Roberto Natalini, ne ho presentata una soluzione elementare, sottolineando come «la probabilità per una persona malata di essere positiva è diversa dalla probabilità per una persona positiva di essere malata».
In conclusione, sono tornata sul gioco d’azzardo con il video di Taxi1729 Il caso si fa bello.

Questa volta in scena ci sono Diego Rizzuto e Olmo Morandi: tutto comincia al casinò di Montecarlo, il 18 agosto del 1913, quando le persone che si trovarono davanti al tavolo della roulette videro uscire 19 neri consecutivi. Su cosa avreste puntato per il ventesimo lancio? Avreste fatto come i presenti e vi sareste giocati anche le scarpe? «La forza di un’anomalia come questa è capace di indurre in tentazione chiunque, persino i più scettici», dichiarano Paolo e Diego nel libro, e nel video sentiamo una fastidiosa vocina che continua a ripetere «Il rosso è più probabile!» Ma il rosso si negò ancora e i neri consecutivi arrivarono a 26. Il motivo per cui avremmo puntato sul rosso è legato all’idea errata di caso che abbiamo in testa: secondo gli psicologi Daniel Kahneman e Amos Tversky «tutti noi abbiamo in testa delle regole estetiche che il caso deve rispettare per potersi dire tale!». L’equità, l’alternanza e il disordine appartengono a quei bias cognitivi di cui siamo tutti vittime, in qualche modo, come dimostrato da Steve Jobs, che, con l’opzione shuffle dell’iPod «decise di correre ai ripari e di creare una riproduzione casuale non “veramente casuale”, ma che apparisse tale ai clienti».
Queste regole estetiche sono così radicate che trovano terreno fertile anche nel gioco del Lotto, con i numeri ritardatari, che sono riportati anche nel sito ufficiale del gioco del Lotto (quelli seguenti sono comparsi il 16 febbraio 2024):

Tendiamo a vedere una dipendenza tra i singoli eventi, ma non tutti gli eventi sono collegati tra loro, e sicuramente non sono collegate tra loro le estrazioni del Lotto. Il Lotto non ha memoria, come la moneta, come i dadi, come la roulette!
Dopo aver cercato di scardinare i bias cognitivi legati alla probabilità a suon di matematica, ho concluso il percorso riprendendo in mano l’articolo (già citato) di Paolo Caressa per parlare di un’altra vicenda giudiziaria complicata dal calcolo (errato) della probabilità, quella «dell’inglese Sally Clark, condannata nel 1999 per aver soffocato entrambi i figli: il giudice aveva stimato troppo improbabile che tutti e due fossero morti in culla, dato che la probabilità che un bimbo muoia di questa orribile sindrome era stimata 1 su 8543». Se noi consideriamo indipendenti tra loro le due morti, come ha fatto il pediatra interpellato, la probabilità, già bassa, di un singolo evento, diventa ancora più bassa quando si considerano i due eventi insieme, «poco più di un milionesimo per cento!» Bisogna aspettare il 2001 per avere l’intervento della Royal Statistical Society, che screditò l’ipotesi del pediatra: «la probabilità della morte in culla di un bambino è ben più alta se un suo fratello ha pure subito questa terribile sorte». Sally Clark venne scagionata nel 2003, ma la sua vita era ormai stata rovinata. Non ha avuto la fortuna di avere dalla sua parte il Dream Team di O.J. Simpson…
Fatto in questo modo, il percorso ha permesso di guardare in faccia i nostri bias cognitivi, dare alla teoria delle probabilità una parvenza umana attraverso il racconto di numerosi aneddoti, impedire che venisse percepito come mero calcolo, mostrare, ancora una volta, che la matematica è ovunque e che per l’educazione civica è una vera fonte di ispirazione!
Verso il futuro
Durante tutto il processo di analisi dei dati, ci siamo resi conto di ciò che avremmo dovuto cambiare, in parte per semplificare il nostro lavoro e in parte per rendere ancora più attendibile la nostra indagine statistica, evitando ambiguità:
- prima di diffondere il sondaggio, potrebbe essere utile farlo compilare ad alcune persone, per valutare la chiarezza delle domande e poter, quindi, procedere con eventuali correzioni;
- formulare delle domande chiuse, semplici, chiare e senza una dubbia interpretazione per evitare errori da parte di chi deve compilare il sondaggio; ridurre il più possibile le risposte aperte per rendere più facile l’analisi dei dati;
- nel caso dell’impiego, inserire delle opzioni di risposta che consentano di ricondurre facilmente la professione alle categorie indicate dall’ISTAT;
- una domanda che abbia per risposta “spesso” o “qualche volta” risulta poco oggettiva: dovremmo precisare quanto è “spesso” dal nostro punto di vista (tutti i giorni? Più volte al giorno?).
Queste riflessioni si riveleranno particolarmente utili nel momento in cui procederemo alla stesura di un nuovo questionario, avente per oggetto la matematica nella quotidianità.
IL NUOVO QUESTIONARIO
Nell’ottica di mettere a frutto quanto imparato con questa indagine e con l’obiettivo di realizzare un nuovo questionario (che però verrà somministrato e analizzato da un’altra classe), ci siamo concentrati sulla presenza della matematica nella nostra vita quotidiana. Nel proporre il questionario non abbiamo potuto non tenere conto di alcuni aspetti legati anche all’ambito lavorativo, perché riteniamo che in qualche modo questo possa influenzare l’uso che se ne fa nel resto della giornata. È più probabile che ricorra alla matematica per la soluzione di problemi quotidiani un docente di matematica, ad esempio, rispetto a qualcuno il cui lavoro non ne prevede una grande applicazione. Per la formulazione delle domande, e soprattutto delle scelte multiple, abbiamo riflettuto sulle varie azioni e sui singoli momenti della giornata, per poter capire quanto la matematica sia parte della nostra vita. Abbiamo analizzato anche le diverse branche della matematica per capire quali potessero essere le loro applicazioni, chiedendo aiuto ad altre persone per arricchire la casistica, in modo anche da avere un’idea di quanto la gente possa essere consapevole delle applicazioni quotidiane.
Per le prime domande, ci siamo volute soffermare su due informazioni personali che abbiamo ritenuto importanti, ovvero il grado di istruzione e la fascia d’età, per poter valutare l’impiego della matematica in funzione del proprio titolo di studio. Per i quesiti successivi, ci siamo concentrate su richieste generali che ci aiuteranno a comprendere quanto la matematica sia riconosciuta dalle persone. La prima domanda è una versione quotidiana di quella proposta alla fine del precedente questionario: al posto di «Pensa che potrebbe lavorare senza matematica?», abbiamo proposto «Pensa che la sua vita sarebbe uguale se non ci fosse la matematica?», mentre la domanda successiva chiede di quantificare l’utilizzo della matematica nella quotidianità.
«Che cosa applica della matematica nel suo lavoro?» è diventata: «In quali attività utilizza di più la matematica?» e abbiamo proposto alcune risposte, collegando l’argomento matematico a un esempio tratto dalla quotidianità. Per trovare le possibili risposte a questa domanda e chiarire i dubbi che ci erano sorti, abbiamo chiesto ai nostri genitori e a conoscenti in quali attività ritenevano che questa disciplina fosse fondamentale: valutare le offerte al supermercato, gestire le finanze personali, modificare una ricetta per adeguarla al numero di persone usando le proporzioni… Tra le alternative possibili abbiamo messo anche i viaggi e lo sport, pensando ai fusi orari, al cambio monetario e alle combinazioni delle squadre durante i tornei.
Abbiamo ritenuto fosse il caso di chiedere con quale frequenza venga usata la calcolatrice per risolvere semplici problemi aritmetici, pensando alle ricette o alla suddivisione del conto in pizzeria, per riuscire a cogliere quanta dimestichezza abbiano le persone con la matematica.
Quella più bella, a nostro modo di vedere, è quella riguardante le differenti competenze matematiche a seconda del luogo in cui si vive: siamo consapevoli che esista una matematica diversa a seconda del contesto in cui si vive, basta confrontare tra loro una tribù indigena e un tipico abitante di New York e ci piacerebbe vedere quale potrebbe essere la risposta a questa domanda.
Ci sono anche tante altre domande, ma non è il caso di rovinarvi la sorpresa…
Conoscenze adeguate?
La domanda numero 6 del questionario ha a che fare con il bagaglio di conoscenze fornito dalla scuola: «La scuola che ha frequentato le ha fornito un bagaglio di conoscenze matematiche adeguato rispetto a quello che deve fare?». Le risposte a disposizione erano cinque:
- Non uso la matematica nel mio lavoro
- Per la matematica che uso, bastavano le elementari!
- Le conoscenze che ho NON sono adeguate: avrei dovuto fare un'altra scuola
- Le conoscenze che ho NON sono adeguate: avrei dovuto studiare di più
- Le conoscenze che ho sono adeguate
A queste 5 risposte è stato assegnato un punteggio da 1 a 5 a partire dalla prima, e poi è stata fatta la media per ricavare il grafico seguente.
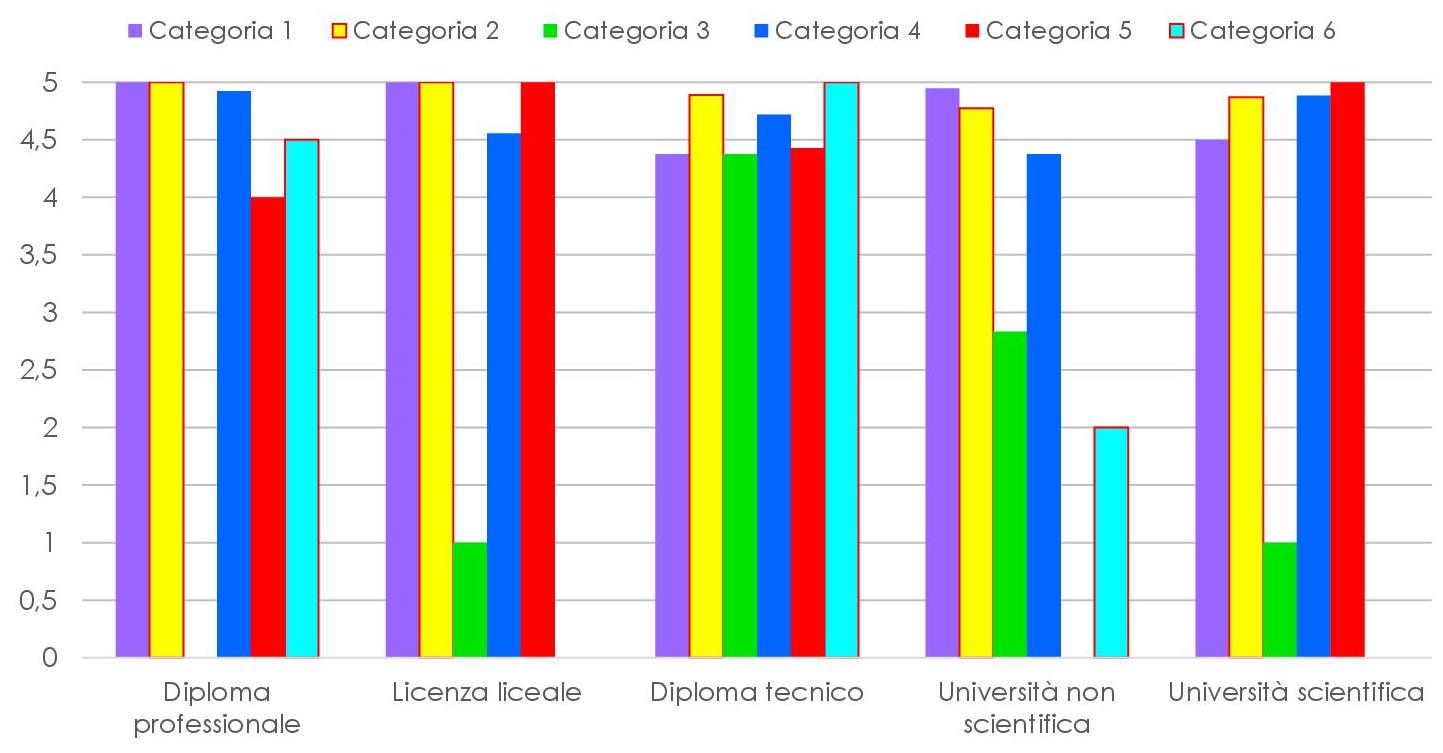
Cerchiamo di interpretarlo dando rilevanza al titolo di studio, riportato in ascissa, mentre i colori riportano l’attenzione sulle categorie. Prima di addentrarci nella descrizione, facciamo alcune precisazioni:
- il commento che segue non vuole essere un giudizio sulla scuola
- come evidenziato nel primo paragrafo, alcune professioni hanno visto un cambio di titolo di studio
- il livello di adeguatezza è percepito, non giudicato obiettivamente
- il percorso professionale scelto, come evidenziato nel paragrafo precedente, è stato fortemente influenzato dal proprio rapporto con la matematica
Analizziamo i risultati, usando due diversi raggruppamenti: prima consideriamo il livello scolastico e poi la categoria.
- Diploma professionale: coloro che hanno risposto al questionario si riconoscono una preparazione matematica adeguata al percorso scelto. Questo potrebbe rispecchiare la realtà delle scuole professionali, dove si addestrano gli studenti a svolgere lavori più che altro pratici, che non richiedono grandi competenze matematiche.
- Licenza liceale: spicca la colonna della terza categoria: si tratta di un’unica risposta, data da un’educatrice, che dichiara di non usare la matematica nel proprio lavoro. Al netto di questa risposta, possiamo dire che la licenza liceale dà competenze matematiche adeguate.
- Diploma tecnico: gli istituti tecnici forniscono conoscenze matematiche adeguate al lavoro per la maggior parte dei propri studenti. Questo potrebbe restituirci il quadro di una scuola che istruisce i propri studenti con competenze matematiche specifiche per il lavoro che dovranno affrontare.
- Università non scientifiche: sembra che le categorie 3 e 6 siano quelle più problematiche: per la categoria 3, le lauree non scientifiche corrispondono a sei educatrici, che hanno risposto come segue: due hanno dichiarato di avere conoscenze matematiche adeguate, una ha risposto di non usare la matematica nella sua professione e tre hanno dichiarato di usare la matematica elementare. Per la categoria 6, si tratta di un’operaia agricola, che dichiara sufficiente la matematica elementare per il suo lavoro.
Se consideriamo il risultato nel suo complesso, possiamo notare che la maggior parte dei laureati sostiene di possedere conoscenze matematiche adeguate al mondo del lavoro, mentre per gli altri, vale il fatto che il percorso scolastico non dà rilevanza alla matematica, che effettivamente non sempre viene usata sul fronte professionale. - Università scientifica: sembra che le conoscenze siano adeguate, tranne che per la categoria 3: si tratta di un’educatrice che ha dichiarato di non usare la matematica nel suo lavoro. Per il resto non ci sono grandi sorprese: è forse scontato ritenere che le facoltà scientifiche preparino gli studenti in maniera adeguata dal punto di vista matematico, ma è bello vederlo confermato dal nostro campione.
Concentrandoci sui colori, ovvero sulle singole categorie, possiamo avere un diverso punto di vista:
- Categoria 1: il primo gruppo comprende avvocati, dirigenti e imprenditori. I ruoli dirigenziali richiedono competenze matematiche, che coinvolgono il processo decisionale, l’analisi dei dati e la lettura dei grafici, mentre per quanto riguarda gli avvocati, è altro ad avere più peso. Il grafico ci dice che chi appartiene a questa categoria ritiene di avere competenze matematiche adeguate.
- Categoria 2: si tratta di consulenti, ingegneri, medici e commercialisti e il grafico evidenzia che tutti coloro che hanno risposto al questionario ritengono di avere competenze matematiche adeguate.
- Categoria 3: al nostro questionario hanno risposto principalmente educatrici e agenti di commercio. In entrambi i casi, si tratta di professioni basate più che altro su competenze relazionali, perciò le competenze matematiche non sono molto richieste o basta la matematica elementare.
- Categoria 4: gli impiegati che hanno risposto al nostro questionario si riconoscono competenze matematiche adeguate.
- Categoria 5: a parte il caso dell’operaia agricola richiamata sopra, a questa categoria appartengono diplomati che per la maggior parte dichiarano di avere competenze matematiche adeguate.
- Categoria 6: si parla di artigiani e operai specializzati, che dichiarano di avere competenze matematiche adeguate.
Concludi con le Prospettive future
© 2020 Amolamatematica di Daniela Molinari - Concept & Design AVX Srl
Note Legali e Informativa sulla privacy