Verifica di matematica, classe seconda liceo scientifico.
Argomento: relazioni e funzioni.

Durata: 60 minuti.

Riflessioni didattiche…
Alcune newsletter si scrivono da sole, a causa di un’elevata esposizione alla matematica, e questa potrebbe essere una di quelle. La sovraesposizione è presto spiegata: l’inizio dell’anno scolastico, con la corsa alla preparazione delle prime lezioni potrebbe già costituire un primo passo. Quest’anno mi ritrovo con una seconda e una terza scientifico, che porto avanti dopo averle accolte in prima: nonostante il percorso continui con facce già viste, la riflessione didattica sui miei metodi non ha mai fine. Durante l’estate, complice il libro di Cristiano Corsini La valutazione che educa, ho affrontato questo tema, che mi ha sempre coinvolto tantissimo. Ho ritrovato gli appunti della scuola di perfezionamento in didattica della matematica, alla quale mi sono iscritta all’indomani della laurea, e ho riletto la tesina realizzata al termine del percorso e fatta con il professore di psicologia dell’apprendimento. In quel lavoro, ho parlato della valutazione come di un «trampolino di lancio per raggiungere nuovi obiettivi», perché mentre l’insegnante usa i risultati raccolti per orientare le tappe successive, lo studente può lasciarsi prendere dall’ansia, accrescere la propria autostima o ricevere nuova forza per proseguire. Insomma, la valutazione ha il potere di generare continui cambi di direzione, sia nel lavoro di insegnamento del docente, che nel percorso di apprendimento dello studente, legando indissolubilmente questi due aspetti, che non sono altro che due facce di una stessa medaglia. 

Che cos’è la matematica?
La valutazione ha a che fare anche con il contenuto, in particolare cambia in funzione del percorso fatto dall’insegnante e delle riflessioni sulla sua disciplina. Non è quindi un caso che Ilaria del canale IlariaF Math abbia approfittato di Folle di scienza, il Festival dei divulgatori che si è svolto ai primi di settembre a Strambino, per raccogliere un po’ di risposte alla sua domanda preferita: Che cos’è per te la matematica? Fino ad ora abbiamo le risposte di Stefano Bertacchi, ricercatore nell’ambito delle biotecnologie industriali, che parla della matematica come di uno strumento molto potente per fare previsioni (se seguite Ilaria sui social, potreste già aver visto la risposta) e quella di Federico Benuzzi, insegnante e giocoliere, che ne parla come di un linguaggio stupendo, necessario per poter descrivere ciò che ci circonda. 

W il carnevale!
La seconda causa di sovraesposizione potrebbe essere la mia prima partecipazione al Carnevale della matematica, che ho ospitato sul mio sito. Ho accettato di far parte di questo gruppo di divulgatori della matematica non senza un certo imbarazzo, visto che parliamo di Roberto Zanasi, autore del blog Gli studenti di oggi, La scuola dal punto di vista di un prof di matematica, Flavio Ubaldini, ovvero Dioniso, autore del blog Pitagora e dintorni e di Il mistero del suono senza numero e di Il mistero della discesa infinita, Leonardo Petrillo, autore del blog Scienza e musica, Annalisa Santi, autrice del blog Matetango, i tre Rudi Matematici, noti per l’omonima e-zine e per i loro post sul blog di Le scienze, Mauro Merlotti, autore del blog Zibaldone Scientifico, Maurizio Codogno, prolifico scrittore e ideatore del Carnevale, autore del blog Notiziole di .mau., ma anche di alcuni libri che ho recensito in passato, come Matematica in pausa caffè e Chiamatemi pi greco, e il sito Maddmaths!, che con le sue numerose rubriche arricchisce il web dal 2009. Dietro le quinte ci sono anche altri divulgatori e il fatto che si sia al numero 171 lascia intuire una storia ricchissima, che infatti è cominciata il 14 maggio 2008. Tra gli autori storici del Carnevale non si può non citare Marco Fulvio Barozzi, del blog Popinga, autore della poesia gaussiana citata in ogni carnevale, sulla quale Dioniso crea la cellula melodica.
Il Carnevale della Matematica e la mia newsletter hanno la stessa finalità, con la differenza che gli articoli citati nel Carnevale sono scritti dai divulgatori coinvolti. Visto che la prima parte riguarda il numero del carnevale, mi sono lasciata guidare da Wikipedia, e ho scoperto alcune delle proprietà che ho riportato all’inizio: essendo 171 un numero triangolare, 13-gonale e 58-gonale, ho deciso di lasciare la parola alle immagini realizzate con Geogebra e questo mi ha portato a familiarizzare ancora meglio con i numeri figurati e a rispolverare una riflessione fatta durante l’estate, che riguarda l’impacchettamento delle sfere (o dei tubi), e delle rose di pesche, e quindi i numeri esagonali (che sono di due tipi diversi!). Il tutto è nato da un simpatico dialogo con mio papà, in occasione del compleanno di mia mamma. 

Topologia: passione e fantasia!
La grande esposizione alla matematica, però, come ho già avuto modo di raccontare nello scorso numero della newsletter, riguarda la partecipazione all’imminente Festival di BergamoScienza e, quindi, lo studio della topologia, da diversi punti di vista. Ho già parlato dei pantaloni speciali, ma ho continuato ad esplorare le proprietà matematiche delle superfici topologiche grazie all’uncinetto (ed è da questo che ho deciso di scegliere come tema per il Carnevale “matematica fantasiosa”). Di fantasia, per progettare i laboratori di BergamoScienza, ce ne vuole davvero un bel po’, come abbiamo scoperto da 7 anni a questa parte (visto che questa è la nostra ottava partecipazione al Festival) e come scoprono (a proprie spese) ogni anno i nostri animatori. È necessario mettersi in gioco per produrre idee che possano coinvolgere i ragazzi delle medie o della scuola primaria e per spiegare qualcosa a chi ha meno conoscenze matematiche di noi, è necessario confrontarsi con la propria visione della matematica, e andare oltre quello che ci viene presentato a scuola. Quest’anno, il confronto è stato ancora più acceso, visto l’argomento: gli animatori ne sono stati conquistati! Il 30 settembre e il 1° ottobre vi aspettiamo sul Sentierone a Bergamo per la Scuola in Piazza e poi nei nostri laboratori fino al 15 ottobre. I laboratori sono due: Grafo-mania, dove i grafi vengono esplorati con Geogebra, e Topo-Lab, dedicato agli intrecci vinciani e ai labirinti.
Sapendo del mio lavoro sulla topologia, alcuni contatti mi hanno segnalato la notizia, pubblicata proprio il primo giorno di scuola su Scientific American, della soluzione di un problema di matematica “vecchio” cinquant’anni (le virgolette sono d’obbligo, visto che è quasi mio coscritto). Il problema riguarda la lunghezza minima di una striscia di Mobius, posto nel 1977 da Halpern e Weaver, e risolto da Richard Evan Schwartz. Conquistato dall’argomento grazie a un libro, Schwartz ha trovato che per realizzare un nastro di Mobius bisogna rispettare il rapporto di √3, ovvero se la striscia è larga 1 cm non può essere più corta di √3 cm. L’articolo di Rachel Crowell offre un’ottima panoramica sul lavoro del matematico: Schwartz ha dedicato parecchie energie a questo problema, che avrebbe potuto risolvere già tre anni fa, se non fosse stato per un errore. Ma nel momento in cui ha trovato la soluzione, si è dedicato notte e giorno alla stesura del lavoro. Gli altri matematici citati lodano il coraggio di Schwartz e la sua rara visione della geometria, che gli hanno permesso di ottenere un risultato che sembrava estremamente sfuggente. 

Canali matematici
Nel 2011, Google ha commissionato la creazione di cento canali YouTube per aumentare il traffico. Madonna era tra questi, e la cosa non dovrebbe certo stupire, ma ciò che potrebbe lasciare senza parole è che tra i canali commissionati c’era anche Numberphile, che attualmente può contare su 4.35 milioni di iscritti e che nel 2014 ha creato un secondo canale, Numberphile2. Il canale si occupa di contenuti matematici, in modo molto leggero e simpatico, come dimostra il miglio di cifre del pi greco, realizzato nel 2014, sulla pista di atterraggio di un aereo, dove hanno messo in fila un milione di cifre del celebre numero.
Navigando in rete alla ricerca di idee, mi sono imbattuta (per l’ennesima volta) nel bellissimo canale di ViHart: in questo caso si trattava della serie doodling in math class, nella puntata dedicata ai nodi. La sua parlantina spedita (che rende difficile capire tutte le parole), i suoi bellissimi disegni e la sua energia fanno venire voglia di prendere carta e penna e imitarla. Sapete che anche gli intrecci di Leonardo, di cui i nostri ragazzi parleranno durante la mostra, sono delle specie di doodling e infatti compaiono a margine dei suoi appunti? 

Eventi
La sovraesposizione alla matematica continuerà anche nelle prossime settimane e non solo per BergamoScienza: si comincia con ComunicaMat, il Festival dedicato alla comunicazione della matematica, organizzato dall’Università di Camerino, che si svolgerà dal 4 al 6 ottobre. Tra i relatori Taxi 1729, Lorella Carimali, Franco Ghione (autore di Tau Topologo), Ilaria Fanelli, Paolo Alessandrini, e tanti altri. Alla sua quinta edizione, il convegno avviene on-line ed è ancora possibile iscriversi.
Se abitate nei dintorni di Brescia e avete l’opportunità di ottenere un permesso per assentarvi da scuola, il 19 ottobre ci sarà il Convegno della Mathesis bresciana “Dalla ricerca alla pratica: come è cambiata la didattica della matematica”. Tra i relatori, ci sarò anch’io, con “Matematica e internet: sfide e stimoli”. Le iscrizioni sono aperte fino al 1° ottobre. 

Buona matematica! Ci sentiamo tra TRE settimane!
Daniela 

PS: Come la newsletter “si è scritta da sola”, anche la vignetta mi ha raggiunta da sola, visto che l’ho ricevuta ieri dal prof. Marzocchi dell’Università Cattolica di Brescia. La striscia di Calvin e Hobbes ha per protagonista Calvin, un bambino di sei anni, che ha per «migliore amico, Hobbes, una tigre di peluche che soltanto lui vede come una tigre vivente, antropomorfa e parlante». La traduzione della striscia è la seguente: «Oh bene, un test vero o falso! Finalmente, un po’ di chiarezza! Ogni frase è pura, dolce verità o vile e spregevole bugia! Una o l’altra! Niente in mezzo!»

“Il merlo, il merlo nella luce”
(poesia gaussiana)

Benvenuti all’edizione numero 171 del Carnevale della matematica, dal tema “matematica fantasiosa”! È la prima volta che ospito il Carnevale e, devo ammetterlo, sono un po’ emozionata!

Il 171 si fattorizza 3x3x19: Dioniso, come da tradizione, ha inviato la sua cellula melodica, caratterizzata da un salto di sesta minore, come se il merlo volesse farci riflettere sull’ossimorica qualità di una luce oscura.

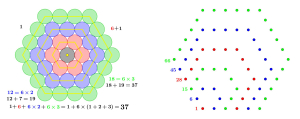
Oltre a essere un gioco di azione e avventura sviluppato da Betagames Group, 171 è un numero difettivo, visto che la somma dei suoi divisori è 89<171. Oltre a essere un numero palindromo nel sistema numerico decimale e nel sistema di numerazione posizionale a base 7 (333), è un numero di Harshad, cioè è divisibile per la somma delle sue cifre. È parte di ben 7 terne pitagoriche, ma sempre come cateto, ed è il diciottesimo numero triangolare, il sesto numero 13-gonale e il terzo numero 58-gonale:

171 è anche il trentaseiesimo numero fortunato, che si ottiene con un crivello simile a quello di Eratostene:

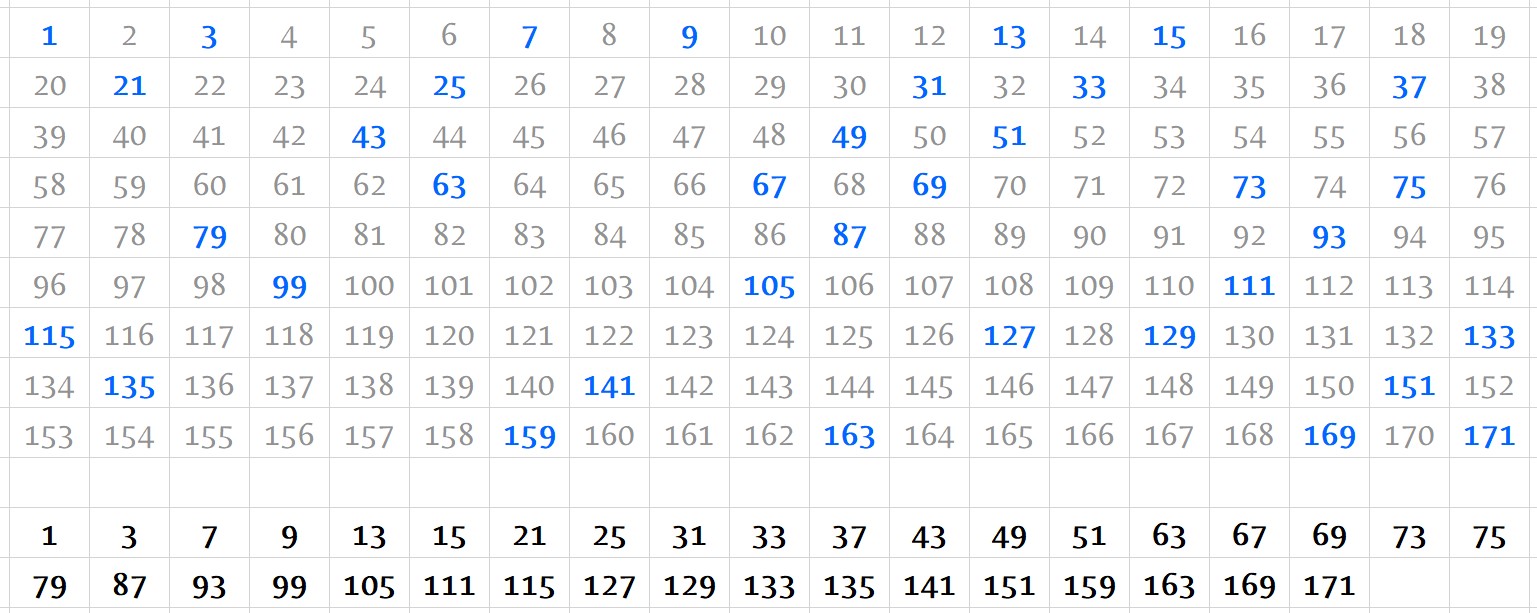
Si tiene l’1 e si tolgono tutti i secondi numeri, ovvero tutti i numeri pari. Il primo numero che si incontra a questo punto è il 3, perciò si contano due numeri e si esclude il terzo rimasto, il 5, e si procede così con 11, 17… fino a 167, nel caso della griglia che ho proposto. Oltre a 1 e 3, ora abbiamo il 7, perciò contiamo 7 numeri (sempre a partire dall’1) ed escludiamo il settimo, dal 19 fino al 165. Ora incontriamo il 9 e procediamo allo stesso modo cancellando 27, 57, 91, 121 e 153. Procedendo con la stessa regola fino a quando possibile, otteniamo la sequenza indicata.

Questi sono i contributi del carnevale:
Roberto Zanasi prosegue la rivisitazione della Divina Commedia in chiave scientifica con Inferno, Canto XIX, dove si parla di inversione di gravità e di Richard Gere poco vestito. 

Dioniso continua ad esplorare il libro I paradossi di Zenone di Vincenzo Fano, che è stato uno dei punti di riferimento per il lavoro di ricerca per il suo libro, Il mistero della discesa infinita. In questa seconda parte, I contributi di Aristotele al paradosso della dicotomia, riporta una sintesi delle considerazioni di Fano relative alle interpretazioni aristoteliche del paradosso della dicotomia. In Guida veloce in città: vantaggi e svantaggi, Dioniso segnala una puntata di Radio3 Scienza, “Andavo a 30 all’ora…”, riassumendo i vantaggi e gli svantaggi in una tabellina, che potrebbe essere estremamente utile a scuola quando si parla di sicurezza stradale, applicazione della cinematica all’educazione civica.

Leonardo Petrillo propone un post dal suo blog Scienza e Musica, di carattere puramente divulgativo, adatto anche a un lettore abbastanza a digiuno di fisica e matematica, focalizzato nell’illustrare un importante modello classico della conduzione elettrica: il modello di Drude (introdotto nel 1900). Nella parte conclusiva dell’articolo, è presente un breve cenno inerente ad una rilevante verifica relativamente recente (2006) del suddetto modello, da parte di un duo di scienziati tedeschi. 

Annalisa Santi ha rispolverato un post di qualche anno fa: dopo il 171 fortunato, sappiamo che in matematica si parla di Numeri Felici, Amici, Socievoli e di Numeri Fidanzati (e ci sono persino i “promessi sposi” 48 e 75), ma Ci sono i Numeri dell’Amore? Per trovare i Numeri dell’Amore è necessario uscire dalla visione matematica ed entrare in quella esoterica. E qui non si pretende certo di definire verità dimostrabili ma di sfruttare, secondo criteri assolutamente indimostrabili e soggettivi, la costanza dei numeri come dato rassicurante nel regno fluttuante dell’amore.

Piotr R. Silverbrahms, a nome dei Rudi Matematici, ha inondato la mia casella di posta elettronica di gentilezza e informazioni, spiegandomi come destreggiarmi in questo nuovo mondo. Il primo contributo è un PM, ovvero un “Paraphernalia Mathematica”, un articolo che tratta di argomenti generali – interessanti e curiosi – di matematica. È la rubrica storica della ben nota e-zine “Rudi Mathematici” (su questo sito, il loro logo è stato ospitato per 14 anni), ed è curata in persona dal fondatore, Rudy D’Alembert. Nel caso specifico, l’articolo fa parte di una piccola serie, chiamata “oltre Platone”, con evidente riferimento a superare i vincoli dei solidi platonici. È la seconda puntata della serie, e il titolo di questo episodio è Ricomincio da tre, un omaggio a Massimo Troisi e un riferimento al fatto che, pur essendo alla seconda puntata, si ricomincia a parlare di triangoli.
Il secondo contributo è un Q&D, ovvero un “Quick and dirty”, una sorta di problema dall’esposizione assai breve e dalla soluzione veloce, anche se il “dirty” specifica che magari, la soluzione, tanto veloce non è. Curve colorate parla di curve chiuse che si incrociano.
Da una rubrica all’altra, arriviamo a quello che, secondo i Rudi, è un “post istituzionale”. Oltre alla famosa e-zine, i Rudi Matematici curano una rubrica sul mensile “Le Scienze”, nella quale propongono un problema: il blog consente al gruppo di mantenere aperto il dialogo con i lettori, che hanno voglia di confrontarsi con il problema proposto e di suggerire le proprie soluzioni. L’ultimo numero di “Le Scienze”, quello di agosto, era il 660 e Il problema di agosto (660) – Mezzogiorno in comune, un problema di percorsi, anzi, di incroci.
Con poca fiducia di riuscire a rispettare i tempi (e chi segue la e-zine sa il perché), i Rudi Matematici disperavano di riuscire a pubblicare altro, ma alla fine è arrivato il 12 settembre 1900: Buon compleanno Haskell!. In questo compleanno, viene davvero celebrata la fantasia, visto che si parte dalle definizioni di Euclide e, percorrendo un sacco di antiche strade romane, si finisce nel bel mezzo della logica combinatoria.

Mauro Merlotti, autore del celebre Zibaldone Scientifico, propone due post: nel primo si parla di curve ad ampiezza costante, cioè di figure che, come il cerchio, hanno la stessa larghezza in tutte le direzioni. Abbiamo bisogno di un po’ di fantasia per capire che se le posizioniamo tra due rette parallele, possiamo farle ruotare mantenendo sempre le rette tangenti alla figura e alla stessa distanza tra loro! Il secondo è dedicato alla pizza al taglio e, dopo aver illustrato diversi modi (non convenzionali) di spartirsi una pizza, Mauro regala un po’ di pizza anche al teorema di Pitagora!

Maurizio Codogno conferma la sua fama di scrittore prolifico e ci regala una lunga serie di quizzini: quadrati alternati, molto semplice, e Vela, facile, ma funestato da una serie di errori; trapezio rettangolo, problemino geometrico facile e dall’1 al 5, una facile somma (se si sa come prenderlo); scegli la scatola è un po’ più complicato rispetto ai precedenti e ha a che fare con i codici a correzione di errore; numeri paladini ha una parte facile e una che richiede qualche conto in più, mentre numeri basici richiede un po’ di conti; il terzo maggior fattore è una semplice (?) applicazione di proprietà di fattorizzazione, primi somma e differenza di primi è molto facile; somme di numeri dispari non primi non è uno scioglilingua ma un quizzino abbastanza semplice, anche se richiede qualche conto, come pure insiemi sum-free; Doubleback Alley non è difficile, ma Maurizio ha trovato divertente ambientarlo; il sistema MIU arriva direttamente dal celebre Gödel, Escher, Bach.
Noto per le sue recensioni anche al di fuori del circuito matematico, durante l’estate Maurizio ha letto Il mistero della discesa infinita di Flavio Ubaldini, un bel romanzo “matematico” di cui si è parlato sopra; L’infinito, di Claudio Ternullo e Vincenzo Fano, che merita la fatica di affrontarne una lettura non semplice; Argomentare di Paolo Artuso, che contiene un utile ripasso della logica. Di Joseph Mazur, Maurizio ha letto Storia del tempo, ma ritiene che gli altri libri di questo autore siano migliori; con Algoritmi, monaci e mercanti di Giorgio Ausiello, si può scoprire come, nonostante tutto, nei mille anni del Medioevo anche in Europa si sia fatta matematica: poca, utilitarista, ma comunque matematica. La traduzione inglese di Arithmetical, Geometrical and Combinatorial Puzzles from Japan di Tadao Kitazawa non è il massimo, ma è interessante vedere giochi per nulla simili ai nostri soliti; Trigonometry – A very short introduction di Glen van Brummelen permette di indagare la trigonometria vista dal contesto della matematica e infine The Britannica Guide to Algebra and Trigonometry, edito da William L. Hosch, è sconsigliato, a meno di non avere curiosità storica su come questi due campi della matematica siano nati e cresciuti.
Per la serie povera matematica, troviamo Mai fidarsi dei fisici che scrivono di matematica, sulle affermazioni un po’ peculiari di Michio Kaku sulle geometrie non euclidee; Come non usare gli Invalsi ci mette in guardia: gli Invalsi mostrano differenze tra varie categorie di studenti, ma se non si specifica come sono misurati i dati, si parla sul nulla. Parlare di Invalsi porta necessariamente a domandarsi: Invalsi: Chi è che non sa leggere e far di conto? E la risposta di Maurizio è la stessa di molti di noi: i giornalisti… Scuole aperte (ma volontariamente) offre un punto di vista diverso sulle vacanze scolastiche estive, visto che segnalare il numero di settimane di sospensione delle lezioni non è statisticamente corretto. Con il post Il senatore Borghi (Aquilini) e il riscaldamento che non ci sarebbe, Maurizio commenta che il senatore Borghi scrive bene e così nasconde le proprie fallacie a proposito del riscaldamento climatico. Il 250% in meno ha attirato l’attenzione di Lucio Malan, che sa fare i conti, ma confonde l’ignoranza con la faziosità, mentre Com’è difficile spiegare ci racconta come a volte la matematica possa fare comodo per confondere un po’ le acque e arrampicarsi sugli specchi.
Per la serie matematica light, Ci sono solo sette numeri la cui radice cubica è uguale alla somma delle loro cifre è una curiosità senza reale importanza; Dati veri ma presentati male riporta la spiegazione di Giulio Betti in merito al grafico sul calo del ghiaccio artico, che è corretto ma fuorviante; Perché non fidarsi delle AI generative, parte N, ci ricorda che a una AI possiamo chiedere tante cose, ma se proviamo a farle fare un po’ di matematica sbaglia peggio di uno studente incapace.

I contributi di Maddmaths! sono come sempre numerosi e variegati:
Sulla cresta dell’onda: intervista con Roberta Bianchini, vincitrice del Premio SIMAI 2023
Roberta Bianchini è ricercatrice all’Istituto per Applicazioni del Calcolo “Mauro Picone” IAC-CNR di Roma. Nel corso del Convegno Biennale SIMAI 2023, svoltosi a Matera, ha ricevuto il Premio Biennale SIMAI 2023 “Fausto Saleri”, per la sua attività di ricerca nella matematica applicata. Il premio è rivolto a ricercatori e ricercatrici under-35. Dopo la premiazione, l’ha intervistata Marco Menale.
Conferenza pubblica di Eduardo Sáenz de Cabezón – Il video integrale
Durante il XXII Congresso UMI che si è tenuto a Pisa dal 4 al 9 settembre scorso, il famoso divulgatore matematico Eduardo Sáenz de Cabezón ha tenuto una conferenza (in inglese) dal titolo molto interessante: How to speak about mathematics to a broad audience, ora disponibile su YouTube.
Archimede 2/2023: speciale valutazione
È uscito il numero 2/2023 della rivista Archimede che è un numero speciale dedicato alla Valutazione. Vi proponiamo il sommario del direttore Roberto Natalini: “Nella continua riflessione sull’insegnamento e sull’organizzazione scolastica, un ruolo spesso trascurato è quello della valutazione. Eppure, senza valutazione è difficile capire se l’azione didattica sia stata efficace, come sia possibile migliorarla e soprattutto non renderla sempre più personalizzata. Per queste ragioni questo numero di Archimede è dedicato proprio alla valutazione, con tre contributi autorevoli e abbastanza complementari tra di loro, per ribadire la complessità della tematica. Apriamo con un articolo di Ketty Savioli, che ci presenta la valutazione “per” l’apprendimento nella scuola primaria (l’articolo è liberamente scaricabile sul sito Mondadori). Segue un articolo molto ben documentato di Rossella Garuti e Nicoletta Nolli su come funzionano e l’impatto che hanno avuto le prove INVALSI somministrate con il computer (Computer based test, CBT). Completa questa rassegna una riflessione di Roberto Ricci, presidente dell’INVALSI, sull’analisi degli apprendimenti in matematica che emerge dalle prove standardizzate. La splendida copertina e il fumetto sono dedicati alla figlia di Vito Volterra, Luisa, e aprono una breve trilogia di Alessandro Bilotta e Dario Grillotti sul matematico fondatore del Cnr che ci accompagnerà per tutto il 2023, un’appedice indispensabile alla loro graphic novel La funzione del mondo – Una storia di Vito Volterra.”
Recenti progressi su un altro problema di Erdős
I problemi posti da Erdős non finiscono mai. Recentemente c’è stato un notevole progresso su un una sua vecchia congettura sulla “densità” degli insiemi di numeri interi. Per saperne di più e capire meglio di cosa si tratta lasciamo la parola al nostro Alessandro Zaccagnini.
Riuscirà la matematica a battere il gerrymandering?
Continuiamo a parlare di gerrymandering, ovvero la pratica fraudolenta che consiste nel formare distretti elettorali in maniera partigiana, in compagnia di Nicola Apollonio.
Un incontro con László Lovász
László Lovász è un matematico ungherese e un Professore Emerito all’Università Eötvös Loránd di Budapest. È stato Presidente dell’Unione Matematica Internazionale ed è stato Presidente dell’Accademia delle Scienze Ungherese. È stato anche uno dei principali collaboratori di Paul Erdős. Raffaella Mulas lo ha intervistato nel giugno 2023, durante una visita all’Alfréd Rényi Institute of Mathematics a Budapest.
Materiali didattici sui mercati finanziari
Pubblichiamo del materiale didattico proposto in un sito web dalla Prof.ssa Rosaria Trisolino, sull’educazione finanziaria che speriamo possa essere utile al lavoro di classe nelle scuole superiori. Precede il riferimento al sito una breve introduzione della docente.
Matematica a fumetti: un nuovo librino di MaddMaths!
Negli ultimi anni sono stati pubblicati tanti fumetti a tema matematica. Con questo nuovo librino di MaddMaths! vi proponiamo una schedatura abbastanza completa di alcune opere recenti appartenenti a questa categoria. L’autrice è Gulsin Celik, studentessa dell’Università di Perugia.
Tre proposte per l’insegnamento della matematica nella scuola
Riprendiamo la discussione sul cambiamento dell’insegnamento della matematica nella scuola proponendovi alcune riflessioni e tre proposte di Giovanni Righini, professore ordinario di Ricerca Operativa presso l’Università degli Studi di Milano, da sempre attivo anche nell’ambito della didattica della matematica.

Eventi:
A Camerino torna Comunicamat – Comunicare la Matematica 2023
Comunicamat 5 – la quinta edizione del congresso “Comunicare la matematica” – ritorna con la stessa formula degli ultimi anni da mercoledì 4 a venerdì 6 ottobre 2023: 3 pomeriggi a distanza, dedicati a interventi sulla comunicazione e la divulgazione della matematica.
Incontri con la matematica n. 37 – dal 10 al 12 novembre 2023 a Castel San Pietro
Ritorna Incontri con la Matematica n.37, il tradizionale Convegno di Castel San Pietro Terme per insegnanti di Matematica, che quest’anno si svolgerà in presenza da venerdì 10 a domenica 12 novembre 2023. 

Letture matematiche
“oltre Marie”: come superare gli stereotipi di genere nella scienza
Il 6 settembre esce in libreria e online “Oltre Marie”, un libro di Nastassja Cipriani e Edwige Pezzulli dedicato alle prospettive di genere in ambito scientifico. Ce ne parla Chiara de Fabritiis (Coordinatrice del Comitato Pari Opportunità dell’UMI).
Rivoluzioni matematiche: il Teorema di Eulero sui grafi
Con il numero di settembre de Le Scienze troverete in allegato il dodicesimo dei venti volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al Teorema di Eulero sui grafi ed è a cura di Alberto Saracco.
Rivoluzioni matematiche: il Teorema dei quattro colori
Con il numero di agosto de Le Scienze troverete in allegato l’undicesimo dei venti volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato al Teorema dei quattro colori ed è a cura di Donatella Iacono e Sabina Milella.
Storia sconosciuta di Évariste Galois, Fabrizio Luccio e Linda Pagli
Brevi consigli per letture matematiche. “Storia sconosciuta di Évariste Galois – matematico e rivoluzionario” di Fabrizio Luccio e Linda Pagli.
L’arte della statistica, David Spiegelhalter
Brevi consigli per letture matematiche. “L’arte della statistica – Cosa ci insegnano i dati” di David Spiegelhalter, consigliato da Marco Menale.
Letture estive consigliate dalla redazione di MaddMaths!
L’estate è spesso tempo di letture ed è sempre comodo avere una lista di libri tra cui poter scegliere. Ovviamente, dati i nostri interessi, queste letture avranno uno sfondo o una motivazione matematica, a volte non troppo stretta, ma sempre presente. Altri consigli li trovate nella nostra rubrica Letture matematiche, che potete trovare a questo link. E poi non smettete dopo l’estate!

La lente matematica di Marco Menale
I criteri di Bradford Hill
I criteri di Bradoford Hill sono utilizzati negli studi statistici randomizzati per riconoscere rapporti di causalità tra grandezze. Perché correlazione non è causalità.
I modelli multiscala
Possiamo descrivere l’evoluzione di un fenomeno a più livelli. Come una lente, ci avviciniamo e ci allontaniamo per vedere dettagli e particolari. È l’approccio dei modelli multiscala. Ce ne parla Marco Menale.
Dinamica delle opinioni: i modelli cinetici
La matematica aiuta a comprendere la dinamica delle opinioni. Dalla loro diffusione, fino a persuasione e polarizzazione. Diversi modelli cinetici sono stati sviluppati negli ultimi anni. Ce ne parla Marco Menale.

È ora di dare il mio piccolo contributo a questa ricca selezione di matematica.
Ho scelto la matematica fantasiosa, perché è la matematica con la quale mi sono confrontata nel corso dell’estate. Dal 2016, l’estate è il momento per me, e per altri insegnanti della mia scuola, per dedicarsi alla progettazione dei laboratori che verranno proposti nel corso dell’imminente edizione del Festival di BergamoScienza (siamo alla sua XXI edizione e si svolgerà nella prima metà di ottobre). Il Festival ha una particolarità che lo rende unico: oltre ad offrire conferenze e incontri con famosi premi Nobel, invita le scuole a mettere a disposizione i propri alunni perché diventino divulgatori scientifici e si facciano carico di far conoscere la scienza ai bambini delle scuole degli ordini inferiori (e, a volte, ai loro coetanei). Da laureati in matematica, abbiamo sempre scelto questa come oggetto dei nostri laboratori, e direi che, negli anni, la nostra scelta si è rivelata vincente! Quest’anno abbiamo scelto la topologia e, nel corso dell’estate, mi sono dedicata… all’uncinetto! Ho realizzato nastri di Mobius e bottiglie di Klein all’uncinetto seguendo due diversi metodi, ho realizzato tori in stoffa e all’uncinetto e, infine, ho cucito dei simpatici pantaloni, seguendo il suggerimento del filmato Topology riddles, al quale sono approdata mentre cercavo materiali sull’argomento. Nel filmato (davvero bello!) si parla di questi pantaloni realizzati da due matematiche della Cornell University, Tara Holm e Lila Greco, e ho deciso di realizzarli. Sui miei pantaloni ho pubblicato anch’io due video: uno short, in cui presento il funzionamento dei pantaloni, e un video più lungo nel quale descrivo (abbastanza nel dettaglio) la realizzazione dei pantaloni, perché qualcun altro possa provare a farlo. La cosa più interessante dell’intero procedimento, a parte i miei errori da sarta dilettante, è che spendere tempo per realizzare queste creazioni mi ha permesso di riflettere sulle proprietà topologiche di questi oggetti, a un livello di consapevolezza che non sarebbe stato possibile in nessun altro modo.
Un ultimo spunto, invece, non ha nulla a che fare con la topologia, ma con i numeri figurati con i quali si è aperto questo Carnevale: in realtà, la riflessione è avvenuta in estate, è nata da un dolce che mi piace preparare, ha coinvolto mio papà, e, come sempre quando si parla con lui, i tubi!

Questo è quanto…
Direi che la rassegna offre matematica per tutti i gusti. Ci si ritrova a ottobre!

La scelta della topologia per la nostra ottava partecipazione al Festival di BergamoScienza mi ha obbligata a fare i conti con questa parte della matematica che non ho mai amato particolarmente.

Eppure... un certo fascino l'aveva! Il nastro di Mobius, ad esempio, mi ha sempre affascinata: prendete una striscia di carta lunga circa 20 cm, alta 3 cm e incollatene gli estremi dopo aver fatto fare una torsione di 180° a un capo. Le caratteristiche di questo nuovo anello sono davvero particolari: se aveste incollato i due estremi della striscia senza aver realizzato la torsione, ne sarebbe uscito un piccolo cilindro, con due bordi e due superfici, quella interna e quella esterna. Il nastro di Mobius, invece, ha un solo bordo e una sola superficie, caratteristica che si può verificare empiricamente, usando una penna e, appoggiata la punta della penna in un punto dell'anello, si scopre che lo si può percorrere in tutta la sua lunghezza, tornando al punto di partenza.

C'è un altro modo per verificare che il bordo è unico: realizzare un nastro di Mobius all'uncinetto con il metodo indicato da Kathy Ceceri, che dà suggerimenti per realizzare un braccialetto. Quello delle foto è qualcosa di più di un braccialetto, visto che ha una massa di 1 kg, essendo realizzato con del filato molto grosso.

Lavorare all'uncinetto per realizzare oggetti topologici mi ha permesso di capire meglio queste superfici così particolari, a partire dal semplice toro (quello che i matematici chiamano toro, ma che il resto del mondo chiama ciambella!). Ho realizzato due diversi tori, uno all'uncinetto e uno, gigante, di stoffa. Sono completamente diversi, e non solo per la tecnica utilizzata: quello a uncinetto ha davvero la forma di una ciambella, con il punto basso che contrasta il punto alto esterno e crea quindi l'arrotondamento, mentre quella di stoffa è stata realizzata con un rettangolo di stoffa, ovvero matematicamente. In questo caso, la struttura non è rigidamente circolare, ma la forma varia a seconda di come viene preso il cuscino.

Ho realizzato, infine, alcune bottiglie di Klein, sempre all'uncinetto, completamente diverse tra loro. Dapprima mi sono imbattuta nel blog Arachne's Loom e grazie allo schema di Ruth, sono riuscita a realizzare un paio di bottiglie davvero simpatiche, che ho provveduto a imbottire di ovatta.

Le altre bottiglie di Klein sono state realizzate in modo diverso: ho unito due nastri di Mobius lungo il loro unico bordo per ottenere una superficie senza bordi, ma ho commesso un errore durante l'operazione. Pur consapevole che i due nastri dovevano avere chiralità opposta, non mi sono resa conto di averli realizzati con la stessa chiralità e ho dovuto scucire una parte del lavoro fatto. Poco importa... ho potuto concludere il percorso con una riflessione didattica, seguendo le fasi che avevano accompagnato la mia presa di consapevolezza. 

Lo spunto per la realizzazione è nato da questa MathArt Challenge e da un video di Numberphile.

A mia mamma piacciono tantissimo le rose di pesche: un po’ di pasta sfoglia (si compra in rotolo, già pronta!), qualche pesca, un paio di cucchiai di marmellata di albicocche e via in forno!
Per il suo compleanno, non potevano mancare…

Ne avevo fatte in quantità e ne sono avanzate 7. Le ho disposte su un piatto, nel modo più “economico” (in termini di spazio) possibile. È la pratica a indicare la strada, ma anche la matematica ci dà una mano:

«Chiunque deve disporre lattine di fagioli in un ampio spazio, può contare su un teorema matematico, noto come Teorema di Thue, secondo il quale la disposizione esagonale permette di raggiungere la massima densità possibile. Pertanto, ancora una volta, come spesso accade con i quesiti matematici, la soluzione migliore risulta essere fondata su una delle strutture più semplici e meglio conosciute.» (R. Eastaway, J. Wyndham, Matematica dietro le quinte, edizioni Dedalo).

Le mie non erano lattine, ma piccoli muffin di pesche, dalla forma tondeggiante, come quelle delle lattine!

Mio papà vede le rose sul piatto. Dice che gli ricordano la Tenaris… strano! Mio papà ha passato quasi tutta la sua carriera lavorativa alla Tenaris e qualsiasi cosa gliela ricorda. Ma questa volta ha ragione: la Tenaris produce tubi e, quando vengono stoccati, sono disposti in modo da occupare il minor spazio possibile, quindi seguendo una struttura esagonale (come quella delle lattine di fagioli!).

«Se il fascio di tubi era più grande, mi pare diventassero 19.»

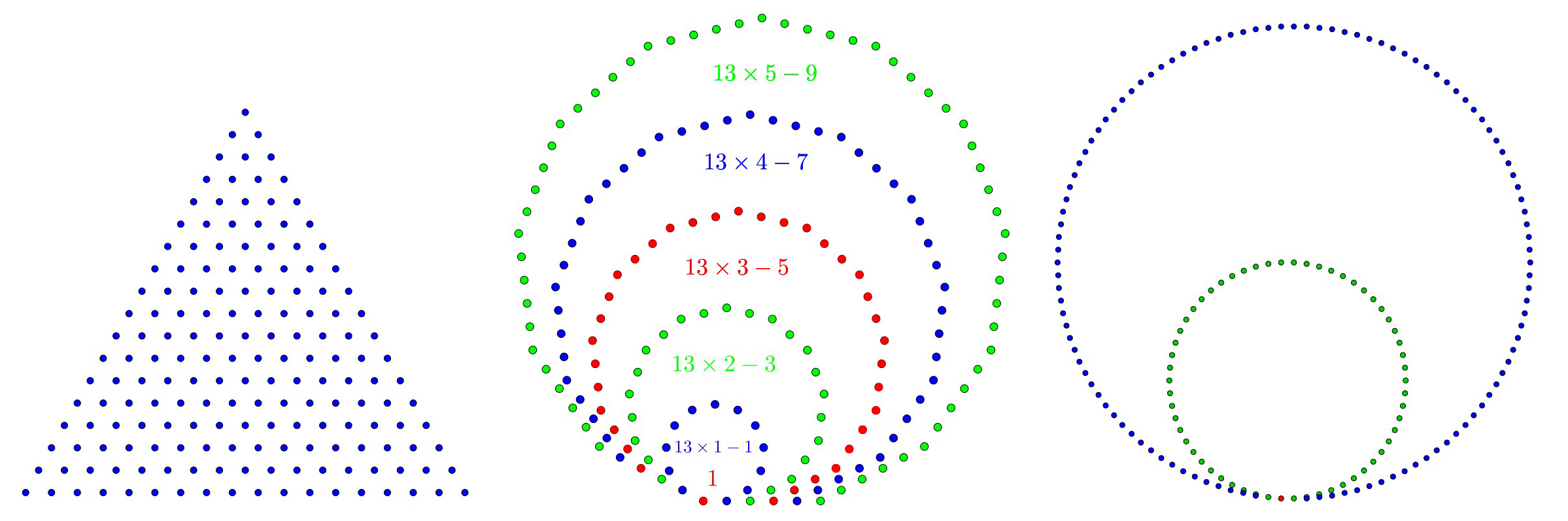
Il successivo numero esagonale è 19, ma sono numeri esagonali particolari, detti centrati. Così la disposizione dà la sequenza: 1, 7, 19, 37, 61, …

La si può costruire in questo modo: il primo numero è 1, poi si aggiunge 6, ovvero 6x1. L’esagono successivo ha i lati con 3 punti ciascuno, i vertici più il punto medio, perciò possiamo dire che l’esagono successivo avrà perimetro 12, in altre parole 6x2. Quello dopo ancora avrà 18 punti, cioè 6x3… e via così. Quindi, all’ennesimo esagono, avremo: 1+6(1+2+…+n-1), se consideriamo come primo esagono quello degenere e ridotto a un punto solo.

Erroneamente, avevo pensato ai numeri esagonali, ma i veri numeri esagonali sono quelli rappresentati nella figura a destra e la sequenza è diversa: 1, 6, 15, 28, 45, 66, …. Come si può notare, crescono più lentamente e danno luogo a un disegno diverso. Non solo: hanno una formula diversa! Io me la sono costruita e se vogliamo arrivare a 66, otteniamo:

1+(6x1-1)+(6x2-3)+(6x3-5)+(6x4-7)+(6x5-9)=1+6(1+2+3+4+5)-(1+3+5+7+9)=66

La riflessione sulla valutazione ha accompagnato il mio percorso fin dall’inizio della mia carriera, forse a causa dei miei trascorsi da studente, tanto che al termine del Corso di Perfezionamento in Didattica della matematica, intrapreso all’indomani della laurea, ho scritto la tesina: «La valutazione in matematica – “Utilizza la valutazione per aiutarti ad insegnare meglio e per aiutare i tuoi studenti ad apprendere meglio”». Il sottotitolo, virgolettato, mi rimanda ad una citazione di cui, però, adesso non so trovare la fonte, ma mi pare riassuma bene anche il libro di Cristiano Corsini, «La valutazione che educa». Ho conosciuto questo libro sui social e ho pensato fosse un buon modo per fare un po’ di aggiornamento nel corso dell’estate. Il mio modo di valutare è sicuramente cambiato molto da quando ho cominciato a insegnare, quasi venticinque anni fa, ma ho realizzato, leggendo le riflessioni di Corsini, che, per quanto certe cose facciano parte di me, del mio modo di fare, da sempre, su altre è importante che lavori ancora.

Per poter incidere positivamente sugli apprendimenti, la valutazione deve avere quattro caratteristiche fondamentali:

• la tempestività, perché solo una comunicazione immediata dei risultati può renderli efficaci ai fini dell’apprendimento
• la chiarezza e la partecipazione, la prima requisito indispensabile per la seconda
• la coerenza tra i criteri valutativi e gli obiettivi
• l’orientamento verso il futuro, perché ogni valutazione diventi un modo per plasmare il futuro

Per quanto abbia sempre considerato necessaria la tempestività (è inammissibile per me somministrare una seconda prova se non ho corretto la prima), non ho mai ritenuto fondamentale la partecipazione degli studenti, anche se l’utilizzo delle rubriche di valutazione nei compiti assegnati su Classroom è sempre stato il mio modo di aiutare i ragazzi ad aver chiaro il mio metro di valutazione e, al tempo stesso, a conformare alle mie richieste con più facilità. Corsini sottolinea più volte questo aspetto: «La valutazione comunica ciò che è importante apprendere, studentesse e studenti tendono ad agire di conseguenza e focalizzano l’apprendimento in modo da rispondere alle domande più frequenti.» D’altra parte, uno dei primi consigli che diamo ai nostri studenti quando si avvicina l’Esame di Stato è quello di ascoltare la prova orale dei loro compagni per avere un’idea di come si svolge, e quante volte durante l’anno scolastico indichiamo il momento delle interrogazioni come occasione preziosa per capire come orientare lo studio?

Mentre leggevo, meditavo e, per aiutare la memoria, sottolineavo, alcuni passaggi hanno creato in qualche modo una risonanza dentro di me, in parte perché ritrovare in parole ciò che penso ha dato maggiore convinzione al mio agire, in parte perché mi ha permesso di cambiare idea sul mio modo di vedere la valutazione. «La valutazione ha il potere di generare conseguenze che possono essere annichilenti o emancipanti», ed è fuor di dubbio che, se valutiamo per riprodurre invece che per trasformare (concetto ripreso in più parti del libro), la nostra rilevazione non potrà essere un aiuto all’emancipazione. Nell’esercizio del nostro potere come docenti, dobbiamo davvero fare attenzione a non mettere al centro del percorso la valutazione, ma il rapporto con i nostri ragazzi: la valutazione deve essere un mezzo, perché il vero fine è lo sviluppo umano del quale abbiamo piena responsabilità.

Come insegnanti, siamo invitati a rinunciare a ogni forma di monarchia (e peggio ancora di tirannia) e a creare spazio per una democrazia partecipativa. Nello Statuto (1998) degli studenti e delle studentesse è scritto che «Lo studente ha diritto a una valutazione trasparente e tempestiva, volta ad attivare un processo di autovalutazione che lo conduca ad individuare i propri punti di forza e di debolezza e a migliorare il proprio rendimento» e se la rilevazione deve guidare l’autovalutazione, lo studente non può che essere parte attiva in questo processo, perché davvero da questo si generi un’emancipazione. Più e più volte Corsini sottolinea come il docente abbia in mano il futuro dei propri studenti: «Per essere formativa la valutazione deve porsi l’obiettivo di dare forma alle attività future», perché mentre tempestività, chiarezza, partecipazione e coerenza sono le caratteristiche della buona valutazione, l’orientamento verso il futuro è ciò che le dà un senso. Nella mia tesina ho parlato della valutazione come di un «trampolino di lancio per raggiungere nuovi obiettivi», perché durante il percorso scolastico, l’insegnante usa la valutazione per guidare le tappe successive, mentre lo studente può lasciarsi prendere dall’ansia, può accrescere la propria autostima, può ricevere nuova forza per affrontare il resto del cammino. Insomma, la valutazione genera continui cambi di direzione sia nel lavoro del docente, sia nel percorso di apprendimento dello studente: insegnamento e apprendimento sono come due facce di una stessa medaglia e non c’è modo di separarle.
Dopo aver elencato tutti gli ostacoli che possono rendere più difficile la valutazione, partendo dal dato di fatto che non può esistere una valutazione oggettiva, Corsini ne dà una definizione, indicandola come misura della distanza tra gli obiettivi del docente e la realtà rilevata nello studente. Citando Dewey (1859-1952), l’autore richiama la necessità di un atteggiamento scientifico, «una qualità che si manifesta in qualsiasi ambito della vita. In negativo, è la libertà dal dominio della routine, del pregiudizio, del dogma, della tradizione acriticamente accettata, del puro egoismo. In positivo, è la volontà di indagare, di esaminare, di discriminare, di trarre conclusioni solo sulla base dell’evidenza, dopo essersi preoccupati di raccogliere tutte le evidenze disponibili.»

L’ultima parte del percorso è dedicata alle prove OCSE, IEA, INVALSI, partendo dal ruolo politico della valutazione, che viene usata in questo caso per misurare l’efficacia di ogni scuola. Aver rinunciato ad una somministrazione campionaria delle prove, estendendole a tutte le scuole del territorio italiano, ha reso le prove inadatte a misurare le competenze, rendendo necessarie (e più snelle per la correzione) le domande a risposta chiusa. Ricordando che una competenza ha sette dimensioni fondamentali (cognitiva, attiva, metacognitiva, emotiva, sociale, situata e dinamica) e che le prove nazionali e internazionali si occupano solo delle dimensioni cognitiva e attiva, l’autore ne mostra il limite, ricordando inoltre che non è possibile giudicare le singole scuole senza tener conto delle iniquità sociali di cui spesso la scuola si fa carico, ma non esita a elencarne anche gli aspetti positivi, come l’aiuto a «confutare empiricamente» lo stereotipo che «vuole le ragazze “naturalmente” meno competenti dei ragazzi in matematica e scienze», riconoscendolo «imputabile al contesto culturale piuttosto che a presunti fattori biologici».
La conclusione è affidata ad esempi e riflessioni inerenti agli strumenti di rilevazione, distinti tra prove oggettive, tradizionali e autentiche, e alle rubriche valutative, fino a chiudere il percorso con la correlazione tra le scelte valutative fatte dal docente e la motivazione. L’ultimo capitolo, riassuntivo, ripercorre le parole chiave del libro, ricordando i «riscontri descrittivi», l’importanza della «comunicazione di indicazioni di miglioramento», il fatto che voto e valutazione non siano sinonimi e che il voto, diverso dalla misurazione, non abbia una sua valenza formativa, ma ricorda anche come sia importante la flessibilità del docente e come la visione meritocratica della valutazione non faccia che generare nuova rigidità.

Confrontandosi con la valutazione nel suo complesso, senza far riferimento alla singola disciplina, l’autore si limita a richiamare la coerenza tra i criteri valutativi e gli obiettivi, ma non sottolinea che la valutazione ha a che fare con il contenuto anche sotto un altro punto di vista, dato che esso dipende anche dall’idea della disciplina che l’insegnante ha sviluppato nel corso del suo cammino. Per il resto, è una lettura necessaria, perché per quanto non si possa condividere tutto ciò che Corsini ha rilevato, è pur vero che una riflessione sulla valutazione è sempre doverosa, visto che essa mette in gioco (e a volte in crisi) il nostro rapporto con gli studenti.

«Non esistono ricette, dunque. Tuttavia, pedagogia e docimologia possono fornire qualche suggerimento utile.»

Verifica di fisica, classe prima liceo scientifico.
Argomento: statica dei solidi e statica dei fluidi

Durata: 120 minuti.

Prova di recupero del debito (settembre)

Verifica di matematica, classe seconda liceo scientifico.
Argomento: operazioni con radicali, equazioni di secondo grado e di grado superiore, sistemi di secondo grado, disequazioni di secondo grado intere e frazionarie, irrazionali e con valori assoluti.

Durata: 120 minuti.

Prova di recupero del debito (settembre)

Verifica di fisica, classe seconda liceo scientifico.
Argomento: cinematica unidimensionale, cinematica del piano e dinamica

Durata: 120 minuti.

Prova di recupero del debito (settembre)

Tempo, creatività e matematica
Il tempo è di difficile definizione: è fuor di dubbio che l’inverno sembri lunghissimo, mentre l’estate si esaurisca in un soffio (soprattutto se la vostra vita ruota attorno alla scuola!), ma non è del tempo come durata quello di cui vorrei parlare: vorrei parlare del tempo necessario a realizzare le cose, il tempo dell’attesa, il tempo impiegato dal lievito per gonfiarsi.
Recentemente Beatrice Mautino, divulgatrice nota sui social come divagatrice, ha guidato una riflessione sul proliferare della divulgazione: «la divulgazione è diventata una cosa anche molto remunerativa […] ma per guadagnare davvero attraverso i social bisogna accettare le regole degli algoritmi che chiedono di avere tanti contenuti (uno o più al giorno), con tempi di fruizione brevi (modello reel)». L’argomento è stato ripreso anche da Dario Bressanini, Ruggero Rollini e tanti altri, che hanno condiviso le proprie esperienze. La pubblicazione frequente genera un abbassamento della qualità e non è difficile intuirne il motivo: per condividere cose di qualità, c’è bisogno di tempo e di creatività e la creatività, appunto, ha i suoi tempi. Parlando di Poincaré in un articolo per Repubblica del 2012, Piergiorgio Odifreddi racconta: «i suoi risultati più famosi, come lui stesso raccontò, gli erano venuti con ispirazioni improvvise: dopo aver bevuto una tazza di caffè, sul predellino di un autobus sul quale stava salendo, passeggiando sulla spiaggia, attraversando la strada... In momenti, cioè, in cui l’inconscio aveva preso le redini del pensiero, dopo che a lungo e consciamente questo si era concentrato sui problemi da risolvere.» A lungo e consciamente, ricorda Odifreddi: la creatività ha bisogno di tempo! 

Tempo di BergamoScienza
Come la chiusura di un anno scolastico, anche la fine dell’estate è tempo di bilanci, e io posso dire di aver speso questa estate a maturare alcune riflessioni sulla topologia: l’abbiamo scelta come argomento per i nostri laboratori di BergamoScienza, ma io non l’ho mai veramente apprezzata a causa di un esame ai tempi dell’università. Abbiamo cominciato il nostro percorso con i futuri animatori, offrendo loro una serie di lezioni propedeutiche in forma di attività o conferenze, a marzo e ad aprile e, al termine dell’anno scolastico, li abbiamo coinvolti in un campus residenziale di tre giorni, durante i quali i ragazzi sono stati invitati a proporre attività e giochi a tema topologico. Questo tempo è servito anche a noi insegnanti per prendere maggiore consapevolezza dei punti cardine che guideranno il nostro percorso. Il Festival si svolge dal 29 settembre al 15 ottobre e questo ci “obbliga” ad un po’ di lavoro estivo: personalmente ho concretizzato la topologia attraverso alcune attività pratiche, unendo la passione per la matematica a quella per l’uncinetto. Tutto è cominciato con una collega che mi ha parlato di una bottiglia di Klein realizzata all’uncinetto: la mia ricerca mi ha fatto accedere a uno schema in Pinterest, ma da questo sono arrivata al blog Arachne’s Loom (la tela del ragno: un arazzo di matematica, musica e arti creative). In uno dei suoi post, Ruth allega lo schema di massima della bottiglia di Klein, ma si lancia anche in alcune riflessioni confrontando lavoro a maglia ed analisi, dichiarando da subito che «Risolvere problemi di analisi, come lavorare a maglia, è un processo meticoloso, e il più piccolo e insignificante errore può rovinare tutto il lavoro successivo. Come lasciar cadere un punto, ad esempio.» Ho ripreso lo schema di Ruth, dopo aver realizzato due bottiglie di Klein, e facendo una descrizione dettagliata di ciò che bisogna fare (sono allegate alla pagina dedicata a BergamoScienza). L’idea era di realizzare un video, ma la registrazione che ho fatto del lavoro non era a fuoco… In realtà, conterei di fare un altro video sulla bottiglia di Klein, ma realizzata in forma più semplice: i due nastri di Mobius necessari sono in preparazione, e li userò come suggerito da quel matto di Cliff Stoll (che a me ricorda un po’ Doc di Ritorno al futuro), che oltre a fare video simpaticissimi, ha anche 1000 bottiglie di Klein sotto la sua casa!
Il mio studio si è reso evidente grazie anche ai pantaloni che ho realizzato, dopo aver visto il filmato Topology riddles, al quale sono approdata mentre cercavo materiali sull’argomento. Nel filmato (davvero bello!) si parla di questi pantaloni realizzati da due matematiche della Cornell University, Tara Holm e Lila Greco, e ho deciso di realizzarli. Ci sono due filmati sull’argomento: nel primo filmato, uno short, presento il funzionamento dei pantaloni, mentre nel secondo descrivo (abbastanza nel dettaglio) la realizzazione dei pantaloni, perché qualcun altro possa provare a farlo. Non sono una sarta professionista, ma una stoffa elastica e una buona macchina da cucire mi hanno fornito un ottimo aiuto, la cosa più interessante, però, è che nel momento in cui spendevo tempo per realizzare queste creazioni, ho avuto modo di riflettere sulle proprietà topologiche di questi oggetti, a un livello di grande consapevolezza, che non sarebbe stato possibile in nessun altro modo. 

Meraviglie di creatività all’orizzonte
Dopo tanto tempo speso in riflessioni (topologiche), la mia creatività è all’apice e mi pare si possa dire lo stesso di tanti miei contatti: Davide e Riccardo del Math-segnale sono “spariti” dal mio radar per un po’, ma ora ne capisco il motivo! Hanno realizzato un bellissimo video, chiaro come sempre e con bellissime animazioni, che ci racconta di una delle tante meraviglie matematiche, la topologia! Dodici: una meraviglia poliedrale è il titolo del video realizzato per partecipare alla terza edizione del Summer of Maths Exposition, organizzato dal canale 3Blue1Brown. La lunghezza del video, il fatto che sia in inglese, e l’argomento stesso (il risultato non è certo banale!) ci obbliga a prenderci del tempo, per poter cogliere fino in fondo la bellezza della matematica e per poter condividere l’entusiasmo che anima Davide e Riccardo!
IlariaF Math ha continuato a proporre contenuti anche durante l’estate ed è riuscita a creare un legame tra le passioni che animano la sua vita: il video che propongo è dedicato al Giappone e, oltre ad essere un resoconto filmato delle sue vacanze, ci regala anche un po’ di matematica, con un simpatico problema di geometria da risolvere, un sangaku. Ho avuto occasione di incontrare Ilaria qui a casa mia nel corso dell’estate e abbiamo avuto modo di parlare un po’ e di confrontarci: è stato un pomeriggio davvero piacevole!
Se si parla di creatività e tempo, non si può non nominare Federico Benuzzi, che approfitta dell’estate per rigenerarsi e per continuare ad allenarsi, dedicando tempo a provare, provare, provare, come ci ricorda in questo video sul senso del suo lavoro e sul senso di spendere tempo per le cose che ci appassionano. Federico ci intrattiene con i suoi approfondimenti sugli argomenti di attualità, come la polemica sull’acqua di Fukushima ad esempio, o con riflessioni, come quella riguardante giornalisti scientifici e divulgatori, che ci racconta anche il suo modo di realizzare video, chiedendo sempre una partecipazione attiva allo spettatore. 

Suggerimenti di lettura
Il primo libro è Il fattore coniglio di Antti Tuomainen, un romanzo che ha come protagonista un matematico attuariale, che legge la vita con le lenti del calcolo delle probabilità e della statistica, perché «fin da bambino avevo capito che la chiave era la matematica. La gente tradiva, i numeri no. Ero circondato dal caos, ma i numeri rappresentavano l’ordine.» La matematica dell’incertezza di Marco Li Calzi ha lo stesso oggetto, ma trattato in forma di saggio: l’autore ha la capacità di rendere accessibile a chiunque la complessità dell’argomento, smontando lo stereotipo secondo il quale la matematica ci può fornire solo certezze. In realtà, la matematica è la nostra arma vincente quando ci troviamo a decidere in condizioni di incertezza e, nella vita di tutti i giorni, decidiamo sempre in condizioni di incertezza! Davide del blog Math is in the air, in occasione dell’uscita del libro, aveva intervistato Marco Li Calzi, ripercorrendo gli argomenti del testo e offrendone così un assaggio ricco di aneddoti e racconti. L’ultima lettura si intitola Slowmath e, purtroppo, non è un libro facile da trovare, visto che non è più in commercio. La rete bibliotecaria mi ha permesso di leggerlo, ma è un peccato che non sia più reperibile, dato che Eugenio Biasin, l’autore, ci mostra con l’esempio il valore del tempo e della creatività in matematica. Il valore del tempo lo percepiamo dalla quantità di recensioni, stimoli e spunti didattici raccolti dall’autore in trent’anni di insegnamento e messi a disposizione di ognuno di noi, un materiale particolarmente ricco per chi si trova all’inizio della propria carriera. La creatività la fa da protagonista e il percorso offertoci da Biasin ci permette di cogliere fino in fondo la bellezza della matematica. 

Buona matematica e buona ripresa delle attività scolastiche! Ci sentiamo tra TRE settimane!

Daniela

PS: la traduzione della vignetta, che probabilmente rispecchia ciò che passa per la testa di molti studenti in questi ultimi giorni di vacanza:
«Sono morta»
«Cosa c’è che non va?»
«Devo leggere questo libro di 280 pagine in tre giorni! Sarà come leggere 70 pagine al giorno! Non posso farcela! Sono morta. Sono morta. Sono davvero morta.»
«Veramente sono 93 pagine al giorno…»
«Ho notato che non mi aiuti mai in matematica quando voglio»
«… virgola tre tre tre tre tre tre tre…»