“Canta, monello”
(poesia gaussiana)

Benvenuti all’edizione numero 178 del Carnevale della matematica!

Come i precedenti, il numero 178 è introdotto dalla consueta CELLULA MELODICA predisposta da Flavio Ubaldini, in arte Dioniso, che l’ha introdotta in questo modo: «Ecco anche la cellula melodica caratterizzata da un impegnativissimo intervallo di quattordicesima maggiore. Pare che il nostro soprano si stia stancando. Dice che vuole essere sostituita da un basso. Vedremo come accontentarla.» 

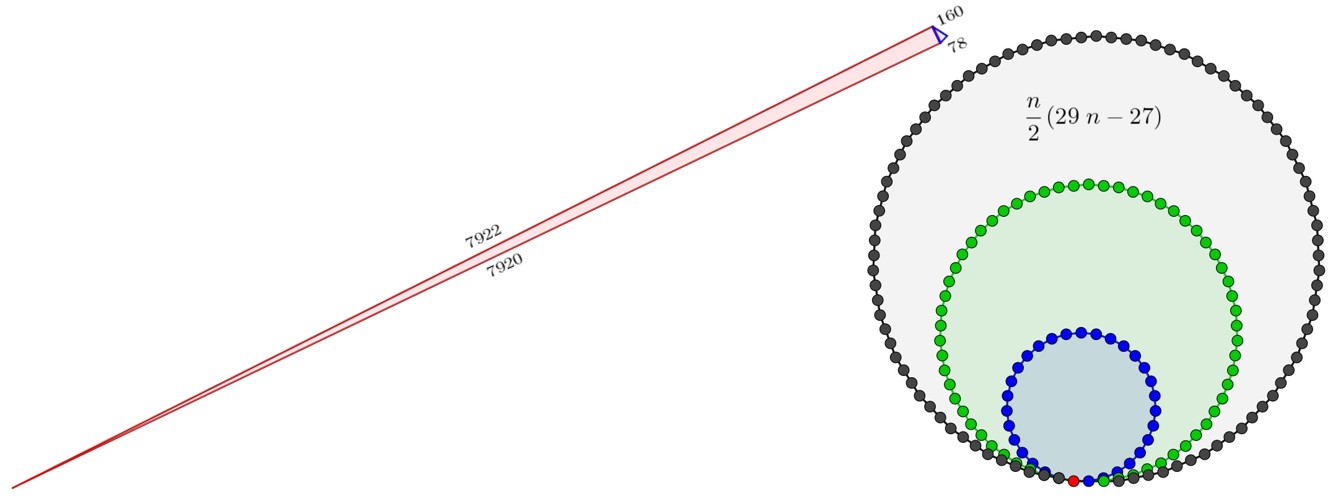
Nonostante la pagina di Wikipedia sia un po’ scarna, al riguardo, devo dire che ricordare le proprietà dei numeri svela sempre qualcosa di interessante. Per cominciare, 178 ha come fattori 2 e 89 – come si vede anche nella cellula – che sono primi di un certo rilievo: 2 è l’unico numero primo pari, oltre ad essere il primo numero primo, e 89 è undicesimo nella successione di Fibonacci ed è un numero primo di Germain, ovvero tale che 2x89+1 sia primo (e infatti il prossimo Carnevale della matematica – spoiler! – sarà primo). Dato che è prodotto di soli due fattori primi, 178 si definisce semiprimo e, come tale, è utile in crittografia, ma è anche omirpimes, ovvero semiprimo non palindromo, anche se è ancora semiprimo quando scritto con le cifre in ordine inverso (871=13x67).
È un numero difettivo, in quanto maggiore della somma dei suoi divisori propri (89 e 2 in questo caso), è il quarto numero 31-gonale, la cui rappresentazione ricorda delle collane di perle e la cui formula ho trovato nel sito MathJoker. 178 è anche cateto minore o ipotenusa in due triangoli rettangoli che, rappresentati, danno una situazione un po’… spinosa!

Il tema di questo 178° Carnevale non poteva che essere “Donne e matematica”: infatti, mentre il Carnevale viene pubblicato il 14 del mese, la scadenza per l’invio dei propri contributi è il 12 e il 12 maggio è, dal 2019, la Giornata Internazionale delle Donne nella Matematica. Grazie a Maryam Mirzakhani, la matematica ha una Festa delle Donne tutta speciale: Maryam è nata il 12 maggio 1977 ed è stata la prima donna ad essere insignita della Medaglia Fields. Dopo la sua morte, avvenuta nel 2017 per un cancro al seno, il 31 luglio 2018, durante il World Meeting for Women in Mathematics, si è deciso di ricordarla con una festa speciale. Come spesso succede in matematica, le giornate speciali offrono un’occasione unica alla divulgazione ed è per questo che sono numerosi gli eventi previsti proprio in questi giorni di maggio. Il sito MaddMaths! offre un elenco dettagliato degli eventi italiani: al momento della pubblicazione gli eventi di Napoli, Torino, Roma, Pisa, Padova, Concesio (Bs), Brescia, Camerino e Roma hanno già avuto luogo, ma mancano all’appello quelli del 15 (a Firenze e a Reggio Emilia), quello del 16 a Roma e i laboratori de L’Aquila, che termineranno il 17 maggio.

Per quanto riguarda il Carnevale, il tema offre l’opportunità di presentare una rassegna di matematiche di tutto rispetto.

Cominciamo con un articolo di Annalisa Santi per il blog Matetango: Chi ha paura di Cecilia Payne? Matematica e astronoma britannica, nata il 10 maggio 1900, è stata vittima di sessismo nella scienza. La sua passione per l’astronomia nasce dopo aver assistito a una conferenza di Arthur Eddington, ma per poterla coltivare deve lasciare l’Inghilterra, nel 1923, grazie a una borsa di studio femminile dell’Osservatorio di Harvard. Fu così che «nel 1925 divenne la prima persona a conseguire un dottorato di ricerca in astronomia presso il Radcliffe College dell’Università di Harvard». Annalisa ricorda che la Payne è stata davvero una scienziata eccezionale che «tutti dovrebbero conoscere al pari di scopritori come Newton o Einstein, a cui lei deve essere associata per la sua altrettanto grandissima scoperta.»
Il secondo contributo di Annalisa Santi è dedicato ad una matematica: Alicia Boole… dai politopi ai numeri politopici. Il numero politopico è un’estensione a più di tre dimensioni del concetto di numero poligonale in due dimensioni, come il 178 che è 31-gonale. Il termine n-politopo è stato coniato da Alicia Boole, figlia di George Boole, il fondatore della logica matematica. Orfana di padre a quattro anni, venne istruita in matematica dalla madre e dallo zio, Charles Howard Hinton, che probabilmente contribuì all’ideazione degli n-politopi. Nonostante la faticosa vita familiare, non abbandonò mai le sue ricerche sui politopi, tanto da riuscire a coinvolgere il matematico olandese Pieter Hendrik Schoute: insieme realizzarono delle tavole e generalizzarono il concetto di poliedri regolari. Per il suo lavoro, ad Alicia Boole venne assegnata una laurea honoris causa nel 1914.

Anche Mauro Merlotti dello Zibaldone Scientifico ha scelto di restare in tema, riproponendo alcuni post nei quali ha parlato di Emmy Noether, la grande matematica «che ha legato il suo nome all’omonimo teorema che mette in luce la profonda connessione tra simmetrie e leggi di conservazione: in un sistema fisico, una particolare simmetria che il sistema possiede è sempre associata alla presenza di una quantità conservata. Ad esempio, se un sistema fisico è invariante rispetto a traslazioni temporali, allora il teorema di Noether implica che l’energia del sistema sia conservata. Analogamente, se un sistema fisico è invariante rispetto a traslazioni spaziali, la quantità di moto si conserva.» Il secondo post ha per protagonista la carica elettrica, il terzo parla di rottura della simmetria (e introduce l’argomento con una citazione di Hermann Weyl e una vignetta di Mordillo impagabili), mentre il quarto approfondisce ulteriormente l’argomento suggerendo anche un paio di letture.

Mauro non manca di ricordare anche il necrologio scritto da Albert Einstein sul New York Times in occasione della morte di Emmy Noether: «Negli ultimi giorni un’illustre matematica, la professoressa Emmy Noether, precedentemente legata all’Università di Gottinga e negli ultimi due anni al Bryn Mawr College, è morta all'età di cinquantatré anni... Nel campo dell’algebra, nel quale da secoli si impegnano i matematici più dotati, ha scoperto metodi che si sono rivelati di enorme importanza per lo sviluppo delle giovani generazioni di matematici... In questo sforzo verso la bellezza logica si scoprono le formule necessarie per una più profonda penetrazione nelle leggi della natura.»

Leonardo Petrillo propone, dal suo blog Scienza e Musica, un post del 2016 dedicato a Sof’ja Kovalevskaya: la vita della grande matematica viene raccontata nei dettagli, a partire dalle pagine delle dispense di Mikhail Ostrogradsky relative al calcolo differenziale e integrale che tappezzavano la sua camera di undicenne, fino al matrimonio di convenienza per proseguire i suoi studi in Germania. Qui, «grazie al supporto di Weierstrass, Sof’ja ottenne il suo dottorato in matematica summa cum laude all’Università di Gottinga.» Le citazioni tratte da I grandi matematici di Eric T. Bell aiutano a seguire le vicende di questa grande matematica, mancata troppo presto per una polmonite. Leonardo conclude riconoscendo che «Kovalevskaya merita un posto di rilievo nella storia della matematica, dato che fu la prima grande matematica russa, la terza donna nella storia a diventare docente universitario in Europa (dopo Laura Bassi e Maria Agnesi), nonché la prima a essere titolare di una cattedra di matematica.»

Ed è proprio di Maria Gaetana Agnesi che tratta il secondo post. Soprannominata Oracolo settelingue, perché a 13 anni parlava 7 lingue, dedita allo studio della matematica e della religione, tanto da trascurare i rapporti sociali, la Agnesi scrisse le Istituzioni Analitiche, ma dopo la morte del padre si dedicò completamente ad opere di carità, trasferendosi al Pio Albergo Trivulzio. Con animazioni che aiutano a visualizzare una spiegazione estremamente chiara, Leonardo ricava l'equazione cartesiana della versiera e non manca di ricordare le applicazioni in fisica, ingegneria e statistica di questa straordinaria curva, simile alla cissoide di Diocle.

In tema con il Carnevale ci sono i due video che ho realizzato per #PeopleForMath, il contest lanciato dal canale IlariaF Math. Il primo, ma ultimo in ordine di tempo, riguarda Sophie Germain, una matematica eccezionale, «un talento straordinario e un genio superiore» come scrive di lei Gauss. È vissuta tra il 1776 e il 1831 ed è la prima donna ad essere stata premiata dall’Accademia delle Scienze di Parigi. La sua vicenda si presta ad essere raccontata come un romanzo ed è quanto ci offre Cecilia Rossi con il libro Sophie Germain. Libertà, uguaglianza e matematica. Così come Sof'ja Kovalevskaja ha dovuto accettare un matrimonio di convenienza, Sophie Germain ha assunto l’identità di Antoine-August Le Blanc per accedere ai corsi dell’École Polytchnique.

Il secondo video ha per protagonista Maryam Mirzakhani, l’eccezionale matematica vissuta tra il 1977 e il 2017. La sua storia mi aveva molto colpito, quando avevo avuto occasione di vedere il docufilm realizzato da George Csicsery “Secrets of the surface” (la maggior parte delle informazioni che ho trovato sono tratte dal film). Purtroppo, non esiste ancora una biografia completa e, a parte la citazione in alcuni libri, ci sono solo libri in inglese, illustrati per bambini, come Maryam’s Magic di Megan Reid e Aaliya Jaleel e Maryam Mirzakhani di M.M. Eboch e Elena Bia. Fortunatamente parecchie notizie le ho trovate nel bellissimo The Mirzakhani Issue, con il fumetto di Davide La Rosa e Silvia Ziche “Sotto il segno del toro” e con gli articoli di Chiara De Fabritiis, Barbara Nelli, Barbara Fantechi ed Elisabetta Strickland.

Un passaggio del film mi era piaciuto particolarmente: nel 2009, dopo aver avuto una prestigiosa Clay Fellowship e una cattedra a Princeton, Maryam approda a Stanford e comincia la sua collaborazione con Alex Eskin, dell’Università di Chicago. È proprio lui a raccontare l’esperienza di lavoro con la Mirzakhani, paragonando il loro percorso a una camminata in montagna. Si tratta di una montagna inesplorata, e, a un certo punto, Alex e Maryam hanno l’impressione di poter raggiungere agevolmente la cima quando un burrone sbarra loro la strada: si tratta di una difficoltà insormontabile. Con un sorriso dolce-amaro, Eskin racconta lo scoraggiamento che hanno provato: quel burrone è costato loro due anni di duro lavoro e fatica. In tutto questo, Maryam si è mostrata positiva, anche se in un anno mezzo non ci fu nessun tipo di progresso. Per affrontare una fatica del genere, è necessario avere una grande stabilità mentale e fiducia in sé stessi.

Dopo questa bellissima carrellata di donne matematiche, procedo con i contributi “fuori tema”, ma sempre in tema matematico!

Piotr R. Silverbrahms, a nome dei Rudi Matematici, è stato il primo a propormi tre contributi e lascio la parola direttamente a lui: 

Diamo i numeri…
Si tratta di un “Quick&Dirty”, ovvero un problemino della serie che raccoglie i quesiti che potrebbero sembrare semplici, ma potrebbero anche essere un po’ velenosi. Questo qui, ad esempio, ha un’esposizione composta da meno parole di quelle che stiamo usando adesso per presentarlo. 

Pesci (e polli) di aprile
Il “post istituzionale”, ovvero quello che riepiloga e fornisce le soluzioni dei lettori al problema proposto sulle pagine cartacee di “Le Scienze”. Stavolta i nostri eroi giocano un vecchio gioco telepatico, uno dei due pensa un numero e l’altro deve indovinarlo. Con qualche complicazione al contorno, naturalmente… 

Buon compleanno, matematici antichi!
Si tratta ovviamente di un “compleanno”, ovvero una sorta di celebrazione a un personaggio, ma in realtà è un po’ diverso dal solito. L’articolo è uscito in RM151, Agosto 2011, con il titolo “Tempio Greco” (pag.3). La situazione in cui è stato scritto è stata parecchio insolita, anzi proprio unica e irrepetibile: di solito i compleanni sono scritti da uno solo dei tre redattori, parlano quasi sempre di un solo scienziato, ed escono nel mese in cui lo scienziato in questione è nato. In questo caso, gli autori sono tre, i personaggi principali celebrati sono ben più di uno, e di nessuno di essi conosciamo la data di nascita. Abbiamo deciso di scrivere un pezzo di compleanno a testa: ognuno si è scelto un greco notevole (non chiedeteci chi ha scelto chi) e ha scritto un brano relativamente breve su di esso. Mentre scrivevamo, ci è venuto in mente che sarebbe stato carino sistemare l’articolo su tre colonne, anziché sulla solita pagina a larghezza normale. Dalle tre colonne siamo passati al tempio, e abbiamo deciso di fare un esercizio tipografico: un “compleanno” a forma di tempio greco (da cui il titolo). Se i lettori più curiosi seguono il link messo poco sopra, dovrebbero più o meno riconoscere la forma: inizia con il timpano triangolare (dove stavano le citazioni, tra cui quella di Virgilio), prosegue con un altro pezzo comune a larghezza normale (più o meno in corrispondenza del fregio e dell’architrave), poi si divide in colonne, appunto le tre colonne tipografiche ognuna delle quali parlava di un matematico. Il pezzo si chiude poi con un altro pezzo a larghezza normale, più o meno in corrispondenza architettonica con il basamento (stilobate?) dei classici templi dorici. A riportare la forma di tempio sul blog non ci abbiamo neppure provato, ci è parsa subito ragionevolmente impossibile. 

«L’uomo che riesce a fare più matematica di dieci divulgatori normali» (così è stato definito da uno dei matematti), al secolo Maurizio Codogno, nonostante i molteplici impegni non delude nemmeno in questa edizione del Carnevale e propone numerosi contributi: 

Ci sono i quizzini, che sono sempre un bel passatempo:
Caselle vicine, in un certo senso un problema di parità
Corda, uno di quei problemi che si possono risolvere col trucco
Tutte le cifre, una specie di gioco a incastro
Successione (non avevo molta fantasia col nome) è di tipo moltiplicativo. 

Le recensioni sono uno dei più grandi contributi di Maurizio Codogno (e potete seguire le sue tracce anche negli store online)

Recensioni della collana Matematica:
L’infinito, di Maurizio Codogno: da Zenone a Cantor e oltre.
I numeri reali, di Salvatore Fragapane. Uno sguardo più diretto su una pura creazione umana.
Le basi dell’analisi, di Davide Calza e Riccardo Moschetti: dalle successioni ai limiti.
Matematica e Musica, di Moreno Andreatta; molto di più di quanto si pensi di solito per le connessioni. 

Altre recensioni:
La teoria dell’informazione, di Giuseppe O. Longo, nella collana kiosk “Lezioni di fisica”: più filosofia dell’informazione che teoria vera e propria. 
Dal bit al qubit, di Carlo Biancardi. La parte quantistica è interessante, l’altra ben difficile da leggere. 

Nel mercoledì matematico:
Triangoli equivoci, dove viene mostrata una variante dell’illusione del quadratino mancante
Negli anni ‘90 i computer usavano un’implementazione della radice quadrata inversa che leggeva numeri reali come se fossero interi.
Quando scommettere sull’arrivo dell'idraulico? Un paradosso forse più psicologico che matematico.
Stavolta mostro come si possano risolvere certi problemi sulle frazioni senza fare conti 

Il contributo di Flavio Ubaldini, autore del blog Pitagora e dintorni, in arte Dioniso, è la seconda parte di Maieutica e duplicazione del quadrato (qui la prima parte). Si tratta di una breve narrazione ispirata al Menone di Platone e l’estratto che ci viene fornito aiuta a farsi un’idea del contenuto:

... «Ma quanto misura allora questo maledetto lato!», starnazzò Eudosso spazientito.
«Non lo so, per Zeus! Non lo so!», fece Menone sconfortato. «Fa freddo! Lasciatemi tornare al lavoro».
«Calma, non scoraggiarti», disse Teeteto mentre Platone rimproverava nuovamente Eudosso.

In altre parole, il processo di apprendimento non è lineare e, al tempo stesso, è ricco di frustrazione e spesso vittima dello scoraggiamento. Aspettiamo la terza puntata per gustarci il senso di vittoria di Menone alla fine del percorso. 

Anche Gianluigi Filippelli, dal blog DropSea, propone le sue recensioni dei volumi della serie Matematica in allegato con la Gazzetta dello Sport:

La statistica di Alessandro Viani
L’infinito di Maurizio Codogno
I numeri reali di Salvatore Fragapane
Le basi dell’analisi di Davide Calza e Riccardo Moschetti
Matematica e musica di Moreno Andreatta 

Gianluigi propone anche un post della serie dei Rompicapi di Alice, Una questione di segni, dedicato ai segni di somma, sottrazione e moltiplicazione, con particolare attenzione alla regola del – * – = +

Dal Caffè del Cappellaio Matto, invece, ecco Topolino #3524: Detective matematico, con all’interno il video di Disney Comics&Science dedicato a una vignetta particolare di una storia uscita su Topolino che ha permesso a Gianluigi di raccontare una piccola storia su Bertrand Russell e la fondazione della matematica. 

Il Carnevale si chiude alla grande con i numerosi contributi di MaddMaths! e lascio la parola direttamente a Marco Menale: 

Dal 2019, il 12 maggio si celebra la Giornata Internazionale delle Donne nella Matematica. Questa data non è stata scelta a caso, anzi. Il 31 luglio 2018, durante l’evento del World Meeting for Women in Mathematics, si è deciso di ricordare la nascita della prima donna a essere stata insignita della Medaglia Fields, ovvero la matematica iraniana Maryam Mirzakhani, che ha ricevuto il prestigioso riconoscimento nel 2014 ed è purtroppo mancata pochi anni dopo.
La giornata del 12 maggio vuole quindi essere un’occasione per “ispirare le donne di tutto il mondo a celebrare i loro risultati in matematica e incoraggiare un ambiente di lavoro aperto, accogliente e inclusivo per tutti” (trad. da qui). Tale scopo è promosso e incoraggiato anche attraverso iniziative di vario genere rivolte a pubblici eterogenei.
Quali sono gli eventi in programma in Italia? Li sta raccogliendo Alice Raffaele in Giornata Internazionale delle Donne nella Matematica 2024 – Tutti gli eventi italiani [AGGIORNATO]. Vi invitiamo a segnalarcene altri mancanti attraverso i commenti o scrivendo a Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo.. 

Nell’articolo I gioielli della Matematica presentiamo un progetto realizzato da Alessandro Zaccagnini con le docenti Maria Chiara Gullo e Lorenza Serventi in due classi dell’Istituto Comprensivo “Guatelli” di Collecchio (Parma) nel quale abbiamo preso alcuni elementi di un laboratorio svolto nell’ambito del Piano Nazionale Lauree Scientifiche nel Liceo Classico “G.B. Romagnosi” di Parma. L’obiettivo finale è dare una dimostrazione “combinatoria” del Piccolo Teorema di Fermat mediante la costruzione di piccoli gioielli. 

Continua la serie La Matematica è piena di Eulero! a cura della redazione di MaddMaths!. Dopo i primi due episodi, infinità dei numeri primi e le equazioni della fluidodinamica, sono fuori:
Episodio 3: La più bella formula della matematica di Chiara de Fabritiis;
Episodio 4: Il problema di Basilea di Sandra Lucente. 

Giovedì 26 marzo 2024 è venuto a mancare a Firenze, dove risiedeva, Enrico Giusti, matematico, storico della scienza, comunicatore. Su MaddMaths l’abbiamo ricordato in due articoli: Enrico Giusti, storico della matematica a cura di Paolo Freguglia e Enrico Giusti e la comunicazione della matematica a cura di Sabina Tessieri, direttrice del Museo “Il Giardino di Archimede” dal 2004 al 2023. 

Save the date: Women and Space ai Lincei – 28 maggio 2024 Si terrà presso l’Auditorio dell’Accademia Nazionale dei Lincei il prossimo 28 maggio il Convegno “Women and Space”, durante il quale si avvicenderanno in una serie di conferenze sei scienziate che hanno contribuito al progresso delle scienze spaziali in diversi settori: osservativo, matematico, tecnico, astronautico e divulgativo. Le oratrici di eccezione sono:

Marica Branchesi (GSSI)
Simonetta Cheli (ESA-ESRIN)
Francoise Combes (College de France/Obs. Paris)
Susanna Terracini (Università di Torino)
Giovanna Tinetti (University College London)
Ersilia Vaudo Scarpetta (ESA) 

Rivoluzioni matematiche: la congettura di Poincaré di Nicola Ciccoli Con il numero di Maggio de Le Scienze troverete in allegato il ventesimo dei trenta volumi della collana dedicata ad alcuni tra i maggiori teoremi matematici. La collana è stata elaborata in collaborazione con la redazione di MaddMaths!. Questo nuovo volume è dedicato alla congettura di Poincaré e alla sua dimostrazione ottenuta nel 2003 da Grigorij Perel’man, ed è scritto da Nicola Ciccoli. 

Per le News di Stefano Pisani:
Scoperto per la prima volta un frattale a livello molecolare I frattali sono ovunque in natura: si possono scorgere strutture frattali nei delta dei fiumi e tra i rami degli alberi. Si tratta di forme che hanno lo stesso sviluppo sia da lontano sia quando vengono viste, ingrandite, più da vicino. Alcuni frattali, detti frattali regolari, sono identici su scale diverse come, per esempio, i vortici dei broccoli romani, ma frattali regolari non sono mai stati individuati a livello molecolare. Fino ad oggi.
Nuovo modello matematico spiega come si muovono i batteri (e il traffico) La marcia di automobili su un’autostrada e il movimento dei batteri verso una fonte di cibo hanno una cosa in comune: in ogni momento possono dare origine a fastidiosi ingorghi che, soprattutto nel caso delle vetture, saremmo lieti si scoprire come sciogliere. La ricerca è stata pubblicata sul Journal of Statistical Mechanics: Theory and Experiment. 

Per La Lente Matematica di Marco Menale:
Armi nucleari, deterrenza e dilemmi Il dibattito sulle armi nucleari torna periodicamente in primo piano. Si parla di deterrenza, ma fino a che punto? A questo dilemma dedicò alcune riflessioni il matematico Anatol Rapoport.
Disuguaglianze e informazione: l’indice di Theil La misura delle diseguaglianze fornisce informazioni per la comprensione di un fenomeno; succede in economica con la distribuzione della ricchezza. Ci sono vari indici per quantificare la disuguaglianza a partire da un insieme di dati. È il caso dell'indice di Theil. 

Per Letture Matematiche:
Chi dice e chi tace, Chiara Valerio Tra ricostruzioni e coperture, una recensione di “Chi dice e chi tace”, l’ultimo libro di Chiara Valerio, che rivela alcune strutture matematiche tra le righe attraverso riferimenti a geometria integrale, ricerca operativa, enumerazione e teoria della complessità, con un pizzico di etimologia. A cura di Alice Raffaele.
In questo libro i conti non tornano È stato pubblicato di recente per le edizioni Einaudi il libro “La seconda prova”. Imparare la matematica vent’anni dopo, scritto da Pietro Minto, che parla del rapporto dell’autore, da adulto, con la matematica. Lo ha letto e commentato per noi Daniele Gouthier. 

Matematica al plurale – oltre il pregiudizio, voci dalla didattica – il trailer del nuovo podcast
Matematica. Se pensiamo a quanti modi ci sono di concepirla, impararla, percepirla nel mondo e nel tempo, che variano da soggetto a soggetto, verrebbe forse da pensarla al plurale: “Matematiche”. Anche perché riguarda tutte le persone: fin dal suo apprendimento, la matematica ha un impatto rilevante sulle nostre vite e spesso si lega a emozioni forti, tra cui la paura di fallire. I voti in matematica continuano a terrorizzare generazioni di studenti e studentesse. Perché succede? Come riconciliarsi con questa disciplina bellissima, ma spesso odiata? Fino a che punto il suo insegnamento può far fronte alle sfide dettate dall’evoluzione tecnologica?
Ne parliamo in Matematica al plurale – Oltre il pregiudizio, voci dalla didattica, un podcast a cura della CIIM (Commissione Italiana per l'Insegnamento della Matematica), in collaborazione con l’AIRDM (Associazione Italiana di Ricerca in Didattica della Matematica), pubblicato da MaddMaths! e disponibile dal 18 maggio sulle maggiori piattaforme di streaming audio. 

L’8 maggio si è svolto nell’aula Carlo Ciliberto dell’Università degli Studi di Napoli Federico II, vista anche la ricorrenza degli 800 anni dalla sua fondazione ad opera del sovrano svevo, l’evento UMI per la Festa delle Donne Matematiche (May12). L’evento, oltre che dall’UMI, è stato organizzato dal Dipartimento di Matematica e Applicazioni “R. Caccioppoli”, con la collaborazione di MaddMaths!, del CECAM e il patrocinio dell’INdAM. Ci racconta com’è andata Chiara de Fabritiis, coordinatrice del Comitato Pari Opportunità dell’UMI, nell’articolo L’evento May12 UMI a Napoli – reportage anche fotografico. 

Questo è quanto…

Direi che la rassegna offre, come sempre, matematica per tutti i gusti!

Verifica di fisica, classe terza liceo scientifico
Argomento: principi della termodinamica

Durata: 120 minuti

«Matematica in campo» è stato pubblicato nel 2023 dalla Casa Editrice Hoepli, nella collana Telescopi. L’autore è Paolo Alessandrini, che, sempre per Hoepli, ha scritto anche Matematica Rock e Bestiario matematico, finalista al Premio Asimov 2022. «Matematica in campo» è entrato nella classifica Book Award 2023 di TuttoSport, ottenendo il terzo posto, ed è stato dichiarato il miglior libro di calcio del 2023.

Paolo Alessandrini riesce a coniugare le sue due passioni, il calcio e la matematica: fin da piccolo, il calcio ha rappresentato per lui libertà e felicità e, avendo notato molti punti di contatto con la matematica, ha scelto di fare questa originale presentazione. Obiettivo del libro è quello di rispondere alla domanda se il calcio sia una scienza o un’arte o, meglio, come specifica nell’introduzione: «un freddo calcolo o una storia d’amore». Effettivamente, se parliamo di scienza, e di matematica in particolare, ci sembra di cogliere una certa freddezza in queste discipline, forse collegata agli algoritmi e alla loro prevedibilità, mentre all’arte associamo un’idea di imprevedibilità, che richiama il mondo delle emozioni. Fin dall’inizio, Paolo Alessandrini invita a riflettere sul fatto che «forse il segreto del successo [del calcio] sta proprio in questa sua duplice essenza».
Il testo è strutturato come una partita immaginaria e il pre-partita coincide con l’organizzazione del tornei, strutturati in gironi all’italiana, a eliminazione o misti: Alessandrini li presenta con diagrammi ed esempi, per mostrare la scelta migliore in funzione dell’obiettivo, usando il calcolo combinatorio e i diagrammi ad albero. Il primo tempo si suddivide in due capitoli, entrambi dedicati alla geometria: si comincia con un grande classico, il pallone, che non è propriamente una sfera, ma è stato a lungo un icosaedro troncato, ovvero un’approssimazione (ben riuscita!) di una sfera. Con sistematicità e ricchezza di particolari, Alessandrini traccia la storia del pallone e delle sue forme, dal teorema di Pogorelov ai solidi platonici ed archimedei, mostrando come tutto tenda a una soluzione ottimale, in equilibrio tra una traiettoria affidabile e un basso numero di cuciture. Il secondo capitolo è dedicato agli errori arbitrali, nei quali spicca come la geometria debba scendere a patti con la fallacia dell’occhio umano, spesso vittima di illusioni ottiche.

L’intervallo è dedicato al calcolo delle probabilità, strumento per indagare la prevedibilità del gioco. Anche in questo caso, lo spettacolo del calcio sfrutta l’equilibrio tra la bravura dei giocatori e il caso: «il calcio è fatto di tanti piccoli episodi, molto spesso imprevedibili e incomprensibili se considerati da vicino. Ma se li osserviamo con una lente grandangolare, li inseriamo in un contesto più ampio e li analizziamo con strumenti matematici evoluti, acquistano un significato e lasciano emergere una struttura logica.»
Nel secondo tempo, diventa fondamentale l’analisi dei dati (come le statistiche che compaiono sullo schermo durante le partite), che ha preso piede a partire dagli errori di Charles Reep, ed è diventata ciò che conosciamo oggi con Valerij Lobanovs’kyj e lo statistico Anatolij Zelentsov. Per quanto l’applicazione della matematica dia l’idea, nell’immaginario collettivo, di un calcio prevedibile e arido, Alessandrini fa notare che «le vere squadre non giocano a caso, ma adottano scelte tattiche più o meno complesse, e lo fanno soprattutto perché è più vantaggioso». Mentre la storia del calcio resta sullo sfondo e permette di capire più a fondo il regolamento del gioco, gli schemi del secondo capitolo fanno intravedere l’applicazione dei modelli matematici e l’impiego dei grafi per lo studio delle reti di passaggi, che aiutano a tracciare le caratteristiche della squadra: l’indice di centralità ci dice come il calcio sia realmente uno sport di squadra, e l’indice di coesione può misurare l’affiatamento tra i giocatori.
La fisica interviene nei tempi supplementari, con il classico moto parabolico e la fluidodinamica, ma è la matematica con la curva perfetta, l’iperbole, che aiuta a individuare la zona migliore per calciare un tiro in rete. Negli ultimi due capitoli, dedicati ai calci di rigore e al post-partita, la protagonista è la teoria dei giochi: attaccante e portiere sono impegnati in un gioco di strategia, nel tentativo di prevedere le mosse dell’avversario, mentre i punteggi assegnati all’esito della partita possono essere studiati nelle loro sfumature grazie alla matematica, che può anche aiutare a valutare il rischio di accordi pre-partita.
Nella sua conclusione, Paolo Alessandrini dà finalmente una risposta alla domanda che ha percorso le pagine del libro, chiedendo, a sé stesso e al lettore, «perché dovremmo avere paura di qualcosa che può aiutarci a comprendere meglio la realtà?». La matematica costituisce uno strumento in più: «la bellezza, se è vera bellezza, è eterna e indistruttibile: l’approccio razionale non ambisce a profanarla, ma soltanto a contemplarla in modi nuovi» e forse il calcio può aiutare a renderci più consapevoli della creatività insita nella matematica.

L’aspetto leggero del testo è enfatizzato dalle citazioni di Vujadin Boskov, l’allenatore più nominato, perché le sue perle di saggezza offrono sempre l’occasione per una risata: «Pallone entra quando Dio vuole»! Numerosi esempi, che ci fanno sentire l’emozione dello sport, costellano la narrazione, mentre la struttura articolata e curata mette in evidenza il rigore matematico, facendo cogliere al lettore lo studio approfondito che resta sullo sfondo, enfatizzato anche dalle immagini, in gran parte realizzate dall’autore, che offrono un supporto a quanto già spiegato nel dettaglio e con semplicità. Se è vero che il calciatore non si affida alla matematica e alla fisica, quanto all’esperienza, all’istinto e alle capacità tecniche, è fuor di dubbio che «la matematica e la fisica offrono strumenti formidabili per comprendere le situazioni che si verificano sul terreno di gioco, ma non dobbiamo dimenticare che esse costituiscono soltanto uno dei possibili punti di vista: in alcuni casi rappresentano una prospettiva privilegiata e preziosa, in altri sono destinate a fornire indicazioni troppo imprecise».

Verifica di fisica, classe seconda liceo scientifico
Argomento: principi della dinamica

Durata: 60 minuti

Aprile, dolce… matematica!
Il mese di aprile ha sempre un sapore particolare per chi vive il mondo della scuola. Per gli studenti, comincia ad avere il sapore della fine dell’anno scolastico, tanto che per qualcuno è il momento di cominciare ad attivarsi per il recupero dell’ultimo periodo. Per gli insegnanti, si comincia a tirare le somme e, almeno secondo il calendario scolastico della mia scuola, quest’anno aprile è volato, cominciando con la coda delle vacanze pasquali, proseguendo con le gite e concludendosi con la Settimana della Cultura classica. Aprile è stato anche un mese impegnativo, visto che si sono chiusi alcuni progetti, forse per questo motivo quando per il Carnevale della matematica 177 è stato scelto il tema Matematica inesauribile, ho voluto parlare dell’inesauribile caparbietà necessaria per avere successo nello studio di questa disciplina. Sono partita dai miei ricordi risalenti alla primaria, alle medie, al liceo, ma soprattutto all’università e ho ripercorso non solo alcune letture fatte nel corso degli anni, ma anche le esperienze di grandi matematici, come Andrew Wiles, che ha dato prova di grande caparbietà per concludere la dimostrazione dell’Ultimo Teorema di Fermat, o come Gigliola Staffilani, full professor al MIT, ripensando in particolare alla domanda rivoltale da Roberto Natalini in un’intervista del 2018 «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?». Forse la matematica inesauribile mi ha richiamato la caparbietà, perché nell’ultimo periodo ho letto molto riguardo a… 

Sophie Germain!
Ho deciso di raccogliere, anche quest’anno, la sfida di IlariaF Math, #PeopleForMath2024 e ho scelto come protagonista Sophie Germain. Per molte delle immagini ho scelto di scansire alcune pagine del libro illustrato scritto da Cheryl Bardoe e illustrato da Barbara McClintock Nothing stopped Sophie, che ha come sottotitolo “La storia dell’irremovibile Sophie Germain”. Il mio primo incontro con Sophie Germain è avvenuto attraverso il libro di Laura Toti Rigatelli, Sophie Germain. Una matematica dimenticata, che mi ha permesso di conoscere Sophie proprio a partire dalla sua corrispondenza e dalle sue riflessioni. Mi ha colpito, ad esempio, la lettera di Delambre, con la quale lui le chiede aiuto per comprare una pendola per Gauss, che ha appunto suggerito: «forse la Signorina Sophie Germain (alla quale vi prego di fare mille complimenti da parte mia) potrebbe avere la bontà di occuparsi della scelta». Il nucleo del filmato è stato sviluppato a partire dal libro di Cecilia Rossi, Sophie Germain. Libertà, uguaglianza e matematica, pubblicato a fine febbraio 2023 dalla Casa Editrice L’Asino d’Oro per la collana “Profilo di donna”. Ho avuto anche l’occasione di confrontarmi con l’autrice in merito ad alcuni commenti sul lavoro di Sophie Germain nei quali mi sono imbattuta durante le mie letture: Piergiorgio Odifreddi, che è noto per il suo umorismo sarcastico, nel libro Il genio delle donne, la definisce una giovane dal «carattere difficile e [dai] modi arroganti», e ne parla come di una presuntuosa, perché «rivolse presto la sua attenzione alle difficili Disquisizioni aritmetiche», mentre Franco Pastrone, del Dipartimento di matematica dell’Università di Torino, in una conferenza riportata come introduzione al libro di Maria Rosa Menzio Il Signor Le Blanc, esprime un giudizio davvero duro nei confronti della matematica. Confrontandomi con Cecilia Rossi, abbiamo riflettuto sul fatto che spesso la caparbietà ha un’accezione positiva nel momento in cui è declinata al maschile, ma diventa un difetto se è una caratteristica femminile. Cecilia mi ha poi citato la canzone di Taylor Swift, The man, che esprime, con leggerezza, proprio lo stesso concetto e mi è parsa così simpatica da meritare un posto all’interno di questa newsletter. 

Aprile, tempo di viaggi di istruzione
Per la prima volta dopo un po’ di tempo, aprile è stato anche il mese dei viaggi di istruzione e non può mancare, quindi, il resoconto di quanto ho fatto con le mie due classi, visto che il tema principale del nostro percorso è stata proprio la matematica. Per la seconda, ho scelto di effettuare una visita, in giornata, a Padova, vista la sua associazione al nome di Galileo Galilei, che vi ha trascorso quelli che ha definito i 18 migliori anni della sua vita. Abbiamo cominciato la visita con Palazzo Bo, dove abbiamo incontrato la figura di Elena Lucrezia Cornaro Piscopia, e poi ci siamo recati al Museo della Natura e dell’Uomo, dove abbiamo fatto il percorso evolution-revolution. Abbiamo pranzato a Prato della Valle e poi abbiamo iniziato il pomeriggio con una visita guidata alla Specola, proseguendo per Piazza dei Signori, dove, mangiando un gelato, abbiamo ammirato l’Orologio Astronomico. Nel rientrare al pullman, siamo passati davanti alla casa di Galileo Galilei e abbiamo concluso il percorso con la Basilica del Santo. Tutta la giornata è stata scandita da forme matematiche, che si sono ripetute più volte e abbiamo trovato anche in ambiti diversi, come l’ellisse del Teatro anatomico e quella di Prato della Valle, le circonferenze dei rosoni della Basilica e dei medaglioni della Sala delle Figure alla Specola, fino alle spirali che abbiamo trovato sia all’interno di Palazzo Bo che al Museo della Natura e dell’Uomo. Tutto questo mi ha permesso di fare una riflessione molto particolare sul ruolo della matematica, fino ad arrivare alla scoperta del libro edito da Il Bo Live, La scienza nascosta nei luoghi di Padova (avrei dovuto conoscerlo prima…).
Città scientifica per antonomasia è Trieste, la seconda città che mi è capitato di visitare, questa volta con la terza, in un percorso che sarebbe stato sicuramente più adatto per una quarta o una quinta, sia per il periodo storico, sia per l’importanza della città dal punto di vista letterario, basti pensare alle statue di James Joyce, Italo Svevo, Umberto Saba e Gabriele D’Annunzio nelle quali ci si può imbattere, autori argomento della letteratura italiana e inglese di quinta. Non solo: anche l’Area Science Park di Padriciano, che abbiamo avuto occasione di visitare, avendo a che fare con la fisica delle particelle si inserisce nel percorso di fisica moderna di quinta, e all’Immaginario Scientifico, oltre al tema dell’energia e della termodinamica, protagonista di molti degli exhibit è proprio l’elettromagnetismo, argomento della fisica di quarta e quinta. 

Didattica della matematica
Mentre la mia scrivania è finalmente un po’ più sgombra, dopo settimane durante le quali è stata invasa dalle guide turistiche di Padova e Trieste e dai libri su Sophie Germain (ormai resta la bibliografia sulla prospettiva di cui parlerò presto), posso distinguere le briciole di un anno scolastico ormai agli sgoccioli. La prossima newsletter potrebbe essere preparata all’indomani del secondo convegno nazionale CARME “Ricerca in pratica: la ricerca in didattica della matematica per la scuola”, che si svolgerà a Pistoia il 17 e 18 maggio, e non vedo l’ora di fare un po’ di riflessione sulla didattica. Nel frattempo, i divulgatori con i quali sono in contatto mi permettono di non mollare mai la presa su questo argomento. Penso, ad esempio, a IlariaF Math, che sta frequentando il corso abilitante per matematica e fisica, e che ha deciso di realizzare brevi filmati per condividere ciò che più la colpisce, come l’importanza del senso di ciò che si apprende, o una breve recensione del libro Didattica della matematica di Anna Baccaglini Frank, Pietro Di Martino, Roberto Natalini e Giuseppe Rosolini. Non posso poi dimenticare l’intervento di Federico Benuzzi nel corso della Settimana della Cultura Classica con lo spettacolo Il metodo infallibile, dedicato al calcolo della probabilità e al gioco d’azzardo. L’argomento, che si presta sia a una riflessione a metà tra la matematica e l’educazione civica, ha suscitato molte domande tra il pubblico, tanto che uno studente ha raggiunto il divulgatore quando tutti se ne erano ormai andati, proponendo la domanda sulla quale Federico ha aperto una riflessione sui social: «Lasciando stare la questione etica, dato che giocando d’azzardo mediamente si perde, perché non passare dall’altra parte?». In più di un'occasione, e se non ricordo male è successo anche questa volta, Federico Benuzzi è stato “accusato” dai follower di essere troppo idealista (basti pensare a quando aveva raccontato di aver stracciato un Gratta e Vinci che gli era stato regalato da un ragazzo tra il pubblico). Credo che per essere bravi educatori sia necessario essere idealisti, in modo da offrire ai nostri studenti la versione migliore del mondo, perché possano realizzare qualcosa di meglio rispetto a ciò che hanno fatto le generazioni precedenti. 

Buona matematica e buon cammino! Ci sentiamo tra TRE settimane!

Daniela

Traduzione della vignetta allegata: “Per dividere le frazioni, usa il reciproco e moltiplica. Perché?” “Perché usare il reciproco?” “No, perché sono nata?”

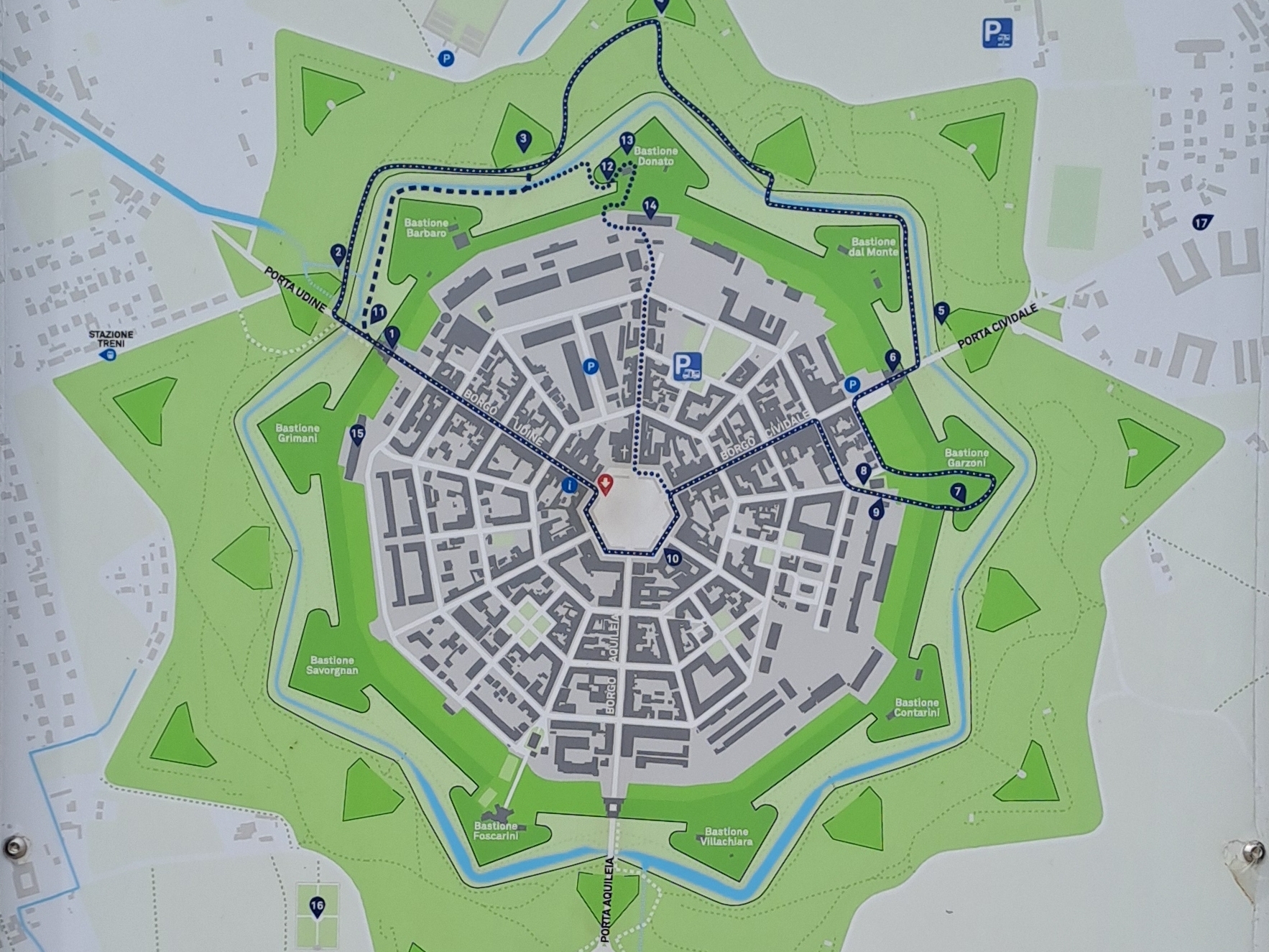
Mi piace organizzare viaggi per le mie classi, perché mi piace mostrare la matematica attorno a noi, nella realtà. Quando scelgo una meta, comincio, quindi, dalla matematica o dalla fisica, perché visitando una città si è immersi, consapevolmente, nell’arte e nella storia, ma si dimentica la componente scientifica, meno visibile, o forse visibile solo per gli occhi più allenati. L’ultima scelta è stata Trieste, ma, durante il viaggio di andata, abbiamo scelto di fermarci prima a Palmanova, la città-fortezza, con la sua stella a nove punte e il suo lato di 400 m che garantiva la possibilità per i cannoni della città di gestire la difesa, mentre il muro inclinato smorzava la potenza dei cannoni nemici, come è stato spiegato nel video di Geopop. Le strutture difensive della città ci hanno regalato degli scorci piacevoli, visto il cielo sereno, che mostrava un bel contrasto con il verde della vegetazione primaverile.

Al centro della città c’è una piazza esagonale, centro proprio della ragnatela, costituita dalle vie che partono a raggio e che si sviluppano in poligoni regolari concentrici. Nelle mura si aprono tre porte e le strade che passano attraverso esse si incontrano nel centro della piazza formando angoli di 120°, in una manifestazione di simmetria che diventa bellezza.

La seconda sosta è stata il Santuario Mariano del Monte Grisa, che domina la città di Trieste e permette, quindi, di vedere la città dall’alto, in un assaggio di ciò che ci aspetta. La struttura in cemento armato è tipica dell’architettura brutalista, che si è sviluppata in Inghilterra negli anni Cinquanta del secolo scorso. Il triangolo è la struttura modulare che si ripete sempre uguale, ma è un triangolo isoscele particolare, con la base uguale all’altezza, ovvero inscrivibile in un quadrato e con un lato obliquo che ha misura pari a metà del lato moltiplicato per radice di 5. Il triangolo ha una forte valenza simbolica per la fede cristiana, richiamando la trascendenza e la Trinità, ma in questo caso va oltre, ricordando la struttura di un alveare e proponendo una A, facilmente visibile, e una M (che ho faticato a far cogliere ai miei alunni), che sono le iniziali di Ave Maria, la celebre preghiera cattolica.

All’interno del Santuario ci sono due chiese, una sopra l’altra e passare da quella superiore a quella inferiore fa sentire schiacciati: come quella superiore fa sentire lo slancio verso l’alto, quella inferiore fa sentire il peso della gravità, e realizza l’intento dell’ingegnere Antonio Guacci, visto che sembra davvero di trovarsi nella stiva di una nave.

Giunti in città, nonostante il maltempo, abbiamo fatto un breve percorso per entrare in contatto con l’anima letteraria della città, quella più nota, quella presente negli antichi caffè letterari e nelle statue di Joyce, Saba, D’Annunzio e Svevo. Visto che il nostro albergo era nel quartiere teresiano, la nostra prima tappa è stato il Canal Grande, dove abbiamo incontrato James Joyce. Su questo canale si affacciano il Tempio Serbo-Ortodosso di San Spiridione e la Chiesa di Sant’Antonio Nuovo, come esempio dell’anima poliedrica della città, che non è solo il punto di incontro di tradizioni diverse - la Slovenia, l’Italia e l’Austria - ma è anche l’incrocio di religioni diverse. Il passo successivo è stato la statua di Umberto Saba, in via Dante Alighieri: il povero poeta è stato privato della pipa, spesso rubata, ma anche del bastone, ma è stato facile immaginarlo percorrere le strade cittadine mentre si dirigeva verso la sua libreria, esempio di ciò che hanno vissuto gli ebrei con le leggi razziali.

Inoltrarsi nella città ha significato anche raggiunge la sua anima più antica, con il Teatro romano, che con la sua apertura semicircolare e i suoi gradoni non può che richiamare la matematica! Piazza della Borsa, il “secondo salotto buono cittadino”, ci ha accolto con la sua eleganza (anche se a me il timpano con l’orologio del Palazzo della camera di commercio ha ricordato l’orologio di Hill Valley in Ritorno al Futuro) e Gabriele D’Annunzio non poteva che starsene elegantemente seduto su una panchina (questa statua è stata ribattezzata la “statua della discordia”). L’ultimo luogo della giornata è stato Piazza Unità d’Italia, con la sua Fontana dei quattro continenti sormontata dalla statua alata che rappresenta la città di Trieste. La Fontana è un simbolo della rinascita della città, visto che era stata spostata per consentire il discorso del Duce, che annunciava la promulgazione delle leggi razziali, ed è stata rimessa al suo posto solo in tempi recenti: è stato facile farsi portare indietro nel tempo, pur cercando di sostituire quel ricordo amaro con quello del presidente Luigi Einaudi, che il 4 novembre del 1954, insieme al sindaco della città, ha aperto i festeggiamenti per il ritorno di Trieste all’Italia.

Il suo ritorno alla normalità in tempi così recenti ha ricordato a tutti che Trieste è la città che è solo da poco tempo e che le ferite che ha subito durante la Seconda guerra mondiale forse non sono ancora del tutto rimarginate. La sosta al Santuario Mariano ci aveva permesso di cogliere questa sofferenza, perché non è possibile visitare il santuario senza ricordarne la nascita, con la risposta di Mons. Santin allo Stato maggiore tedesco: «Si stanno avvicinando da due parti gli eserciti. Resistere per farsi ammazzare e per distruggere Trieste? Questa città è la porta d’Europa centrale; perché distruggerla senza alcun scopo? Non è una città germanica; voi, tedeschi, pensate a difendere quelle. Questa è una città italiana, e gli italiani non avrebbero mai dimenticato.» (27 aprile 1945) Dopo aver individuato tutti i palazzi che si affacciano sulla Piazza, dopo aver raccontato della torre campanaria e dei due mori Micheze e Jacheze, e averli sentiti scandire il trascorrere del tempo, abbiamo volto lo sguardo al mare, il quarto lato della piazza, a significare l’apertura della città al mondo.

L’Immaginario Scientifico è stato il punto focale del secondo giorno di visita, visto che l’intero viaggio è stato costruito attorno alla disponibilità del museo: la visita è andata ben oltre le aspettative di noi insegnanti, visto che al termine della mattinata è stato difficile allontanare i ragazzi, che si sono mostrati coinvolti e incuriositi, entusiasti delle attività, delusi da quella che è sembrata una permanenza troppo breve. Durante la visita, abbiamo affrontato il percorso sull’energia con un laboratorio che ha permesso di focalizzare l’attenzione sulle energie rinnovabili, realizzando l’elettrolisi e studiando il funzionamento dei pannelli fotovoltaici, variandone l’inclinazione e la distanza rispetto alla fonte di luce e calore, e attraverso l’inserimento di filtri colorati.

La seconda parte del percorso ha visto come protagonisti i vari exhibit che hanno permesso ai ragazzi di toccare con mano la scienza, di sperimentarla in prima persona, esplorando e divertendosi. La prima parte del percorso ha permesso a tutti di cogliere la centralità della scienza nella città di Trieste, a partire dalla figura di Paolo Budinich, che insieme ad Abdus Salam, fondò a Trieste il Centro internazionale di fisica teorica. Con la prima mappa, topologica, i ragazzi hanno potuto vedere i collegamenti tra i vari scienziati, il loro ruolo nel Sistema Trieste, la presenza di un esiguo numero di donne, ma l’importanza della ricerca scientifica in questa città, visto che se la media in Italia è di 5 ricercatori ogni 1000 persone, a Trieste è di 37. Il piano superiore della struttura ha permesso di esplorare la matematica con il gioco: tassellazioni e puzzle, serie di Fibonacci, cubi di binomi e quadrati di trinomi, simmetrie con la simpatica scrittura allo specchio, la camera oscura, le illusioni ottiche… insomma, così tanta matematica da lasciare inebriati!

La meta successiva, nel pomeriggio, è stata la Grotta Gigante: la grotta non è solo magnificenza e bellezza indescrivibile, ma anche laboratorio scientifico, come ci ricordano i due pendoli centrali, usati per le rilevazioni sismiche.

La giornata si è conclusa con un ulteriore giro in città: ci siamo fatti lasciare alla Cattedrale di San Giusto, in cui il rosone centrale ha rimandato alla matematica (ovviamente!), ma ha anche evidenziato la mancanza di simmetria della struttura. Una mancanza presente anche all’interno, visto che le colonne che separano le navate sono spaziate in modo diverso ai due lati dell’altare. I ragazzi hanno notato questa rottura della simmetria, evidenziandola come mancanza di bellezza!

Dopo la salita al castello per vedere da vicino i due automi originali, Micheze e Jacheze,

siamo ridiscesi lungo la strada antistante la cattedrale, verificando la distanza in passi dall’Arco di Riccardo. Ci siamo soffermati sul nome dell’arco, ma la mancanza di simmetria (successiva alla sua costruzione) è stata poco notata: i ragazzi cominciavano a scalpitare, assaporando il momento di libertà che abbiamo concesso loro dopo aver raggiunto l’inetto triestino, Italo Svevo.

L’ultimo giorno di visita è stato un’oscillazione tra presente e passato, avendo scelto di lasciare ampio spazio ad entrambe le anime della città: abbiamo visitato l’Area Science Park di Padriciano, all’origine un campo profughi, dove i ricercatori Alessandro e Pietro, insieme allo studente della magistrale di fisica Nicolò, ci hanno guidato alla scoperta dei lavori che vengono svolti all’interno dei laboratori dell’INFN. Dopo averci parlato della fisica delle particelle e averci tratteggiato il quadro storico, estendendo il discorso fino al CERN, hanno permesso ai nostri studenti di capire cosa significhi studiare le particelle, anche attraverso il confronto tra le strumentazioni in uso nel passato e quelle più moderne. In una sala riunioni, gli studenti hanno poi potuto fare domande, in un piccolo percorso di orientamento.

La seconda parte della mattinata ha avuto per protagonista il Monumento Nazionale delle Foibe di Basovizza. Lo storico che ci ha accompagnato in questo percorso ha fatto in modo che potessimo cogliere nei particolari la storia più recente della città, a partire dalla fine della Prima guerra mondiale fino ai giorni nostri. Il passato delle foibe è un passato che è ancora presente, se pensiamo anche solo a quanto ci ha raccontato lo storico della sua esperienza: quando fa la guida a Basovizza viene etichettato come fascista e quando si ritrova a fare la guida alla Risiera di San Sabba viene etichettato come comunista. La riflessione che è stata sollecitata è andata ben oltre i luoghi visitati e il tempo studiato, mentre il monumento, con le sue linee scarne ed essenziali, ha richiamato le macchine della fisica che avevamo visto in piazza a Palmanova: in quel caso erano servite per costruire le fortificazioni della città, in questo sono state utilizzate per calarsi all’interno della foiba a carpirne i segreti. Questa comunicazione tra interno della foiba e mondo esterno è stata bloccata da un coperchio che, con la sua fissità e la ruggine, dà l’idea di un evento fermo nel tempo, lontano ma al tempo stesso vicino.

La visita alla città di Trieste ci ha permesso di notare come il linguaggio della matematica, astratto e simbolico, possa essere lo strumento ideale per comunicare attraverso i simboli, basti pensare al Santuario Mariano del monte Grisa. Il rigore della matematica, inoltre, può diventare espressione di regolarità e bellezza, presente in Piazza Unità d'Italia, è stata manifestazione di eleganza e maestosità, mentre la sua assenza, come nella Cattedrale di San Giusto, ha segnalato una mancanza di armonia. Mi ha colpito il fatto che Trieste sia nominata soprattutto come città letteraria, mentre la sua essenza è, ancora una volta, più articolata e poliedrica di quanto sia possibile cogliere con un primo sguardo: Trieste è una città scientifica, e spesso il turista medio coglie “solo” la bellezza artistica, senza rendersi conto che l’arte sceglie la matematica per enfatizzare certi aspetti. Federica Manzon, nella guida di Trieste del Touring Club, scrive: «A scuola ci insegnavano le poesie di Rilke che a Duino inseguiva l’Angelo del Tempo, poi Svevo ovviamente e ci portavano in visita alla libreria antiquaria del poeta [Saba]. Nei caffè non mancavano mai le presentazioni di qualche autore cittadino, meglio se poco noto nella nazione. Così una generazione dopo l’altra è cresciuta nel culto della città di carta e la letteratura è considerata patrimonio del Dna triestino: un mito tutto rivolto al passato, un culto dei morti poco celebrati in vita. Passa invece del tutto sotto silenzio la presenza in città di uno degli avamposti scientifici più importanti al mondo.» Così Trieste, connubio di tradizioni (Slovenia, Austria, Italia), incontro di religioni, diventa anche culla delle “due culture”, l’anima umanistica e quella scientifica, che ognuno di noi porta dentro di sé, ne sia consapevole oppure no.

Durante la costruzione del percorso di visita ho letto dell’impegno di Abdus Salam, quello che Pietro Greco definisce il pakistano visionario, che «propose di allestire un centro dove formare alla fisica teorica i giovani più valenti dei paesi in via di sviluppo. Non solo per il valore culturale intrinseco di una simile iniziativa, ma anche perché la scienza è il motore dello sviluppo economico. E la scienza di base è il primum movens della scienza. In altri termini – questo era il pensiero di Abdus Salam, in controtendenza rispetto a molto analisti – i paesi in via di sviluppo non possono fare a meno di eccellere anche nelle scienze più astratte se vogliono recuperare il gap economico che li separa dai paesi più avanzati.». Ci è stato fatto notare come l’eccellenza di Trieste sia diversa dall’eccellenza americana: per accedere alle grandi università statunitensi, devi dimostrare di essere all’altezza, mentre Trieste apre le proprie porte a chi questo sapere lo vuole costruire, per portarlo poi nel proprio paese di origine, per permettere anche ai paesi meno fortunati di costruirsi un futuro.

Fotografie realizzate durante il viaggio di istruzione a Trieste, il 17, 18 e 19 aprile 2024, con le classi 3AS e 3ES.

La scelta di visitare Padova, con una seconda liceo scientifico, non è certo stata casuale, considerati i 18 anni che Galileo Galilei ha passato in questa città (i migliori della sua vita*). Padova può, quindi, essere considerata la culla della scienza moderna e, visto che in seconda liceo scientifico in fisica si affronta lo studio della cinematica, che si completa poi, nella seconda parte dell’anno, con la dinamica, Padova diventa una tappa obbligata.

Il passaggio da Palazzo Bo è stato il primo passo alla scoperta di questa città, in un percorso che si è arricchito di matematica ad ogni passo.

A Palazzo Bo abbiamo avuto modo di visitare il teatro anatomico, con la sua struttura ellittica a cono rovesciato, come un anfiteatro romano, con sei ordini concentrici. Ripensando alle dimensioni della struttura, non si può non rimanere colpiti dall’illusione ottica che fa percepire il teatro come se fosse più piccolo. Le sei ellissi accoglievano gli studenti che dovevano assistere alle autopsie e potevano contenere fino a 250 spettatori.

Il teatro anatomico fotografato dal basso verso l’alto, e il modellino presente nell’anticamera, che permette di coglierne l’intera struttura.

L’ellisse ci ha accolto anche a Prato della Valle, dove ci siamo recati per un pranzo sul prato: con i suoi 90.000 m² è una delle piazze più grandi d’Europa e le 88 statue (in realtà, dopo il passaggio di Napoleone, 78) permettono di incontrare il matematico Giovanni Poleni e anche Galileo Galilei, al quale manca il dito medio della mano destra.

La statua n° 36, raffigurante Galileo Galilei, e uno scorcio del canale che delimita il parco

Purtroppo, la struttura di Prato della Valle si può cogliere bene solo osservandola dall’alto, e per quanto sia stato meraviglioso il panorama che abbiamo goduto dalla Specola, il nostro sguardo non ha potuto raggiungere Prato della Valle.

La Specola di Padova è stata sede dell'Osservatorio Astronomico ed è ora una delle più importanti strutture di ricerca dell'Istituto Nazionale di Astrofisica. Nella Sala della Meridiana, abbiamo potuto ammirare le ellissi delle orbite dei pianeti (tra i quali, vista l’antichità del dipinto, mancano Urano e Nettuno – insieme a Plutone, pianeta-nano) nell’affresco del sistema solare. Non può mancare, nella stessa sala, l’analemma (più propriamente lemniscata) che, con la sua forma a 8 deformato, descrive la posizione del Sole nei diversi giorni dell’anno.

L’affresco del Sistema Solare e la meridiana tra i piedi degli studenti

Dalle ellissi alle circonferenze il passo è breve, visto che la circonferenza è un’ellisse con i fuochi coincidenti. Nella Sala delle Figure, sulle pareti troviamo rappresentati, a figura intera, otto scienziati, Tolomeo, Copernico, Tycho Brahe, Galileo, Keplero, Newton, Montanari e Poleni. Secondo quanto riportato nella nota numero 9 di questo lavoro di Valeria Zanini, L'eredità scientifica e culturale di Giuseppe Toaldo, a 300 anni dalla nascita, «Giovanni Santini (1787-1877), terzo direttore dell’Osservatorio, decise che la volta fosse ridipinta con una serie di cerchi concentrici di stelle su sfondo azzurro. Tutto attorno furono dipinte, in medaglioni, le effigi di sedici celebri astronomi e matematici: Ipparco, Tolomeo, Copernico, Galileo, Keplero, Cassini, Newton, Maraldi, Bradley, Herschel, Lagrange, Laplace, Bessel, Gauss, Piazzi, Oriani.» Anche il quadrante presente nella Sala delle Meridiane riporta alla circonferenza, trattandosi di un quarto di cerchio, ma ce n’è uno anche nella Sala delle Figure.

Con le sue cupole e i suoi rosoni, anche la Basilica del Santo ci parla di circonferenze.

A Palazzo Bo abbiamo ritrovato anche una spirale, nella stele di Giò Pomodoro dedicata a Galileo Galilei, ma la spirale ha dominato anche tra fossili, ammoniti e chiocciole al Museo della Natura e dell’Uomo, lungo il percorso Evolution-Revolution.

All’inizio della nostra visita guidata al museo, ci siamo imbattuti in una lemniscata (o in un simbolo di infinito, se preferite) come a farci presente, fin da subito, che il percorso dell’evoluzione non avviene in linea retta. Al tempo stesso, le dimensioni ci hanno permesso di notare come l’uomo costituisca solo un piccolo tassello, visto che occupa un piccolo segmento nel Quaternario.

Della nostra visita a Palazzo Bo vanno sottolineate, in chiusura, due cose: la prima è la statua di Elena Lucrezia Cornaro Piscopia, prima donna al mondo a ottenere una laurea, il 25 giugno del 1678. Un ricordo di lei è presente anche nella Cattedrale, in quanto oblata benedettina. Citando la voce a lei dedicata su Wikipedia: «Figlia di un nobile della Repubblica di Venezia che ne favorì in tutti i modi l'educazione, a diciannove anni prese i voti come oblata benedettina, proseguendo gli studi di filosofia, teologia, greco, latino, ebraico e spagnolo. Ormai nota agli studiosi del tempo, a partire dal 1669 fu accolta in alcune delle principali accademie dell'epoca. Quando il padre chiese che la figlia potesse laurearsi in teologia all'Università di Padova, il cardinale Gregorio Barbarigo si oppose duramente, in quanto riteneva "uno sproposito" che una donna potesse diventare "dottoressa", perché avrebbe significato "renderci ridicoli a tutto il mondo".»

L’ultimo ricordo che portiamo con noi, al termine di questa visita, è la Scala del Sapere di Gio Ponti: rappresenta il cammino della conoscenza di ogni studente durante la sua carriera e il termine, «Ancora imparo», in cima alla scala – dove ritroviamo uno studente ormai anziano che non è più nemmeno in grado di reggere i libri – ricorda a tutti noi che la vita stessa è un percorso di apprendimento che non ha mai fine.

Questo è solo un assaggio di ciò che si può trovare a Padova: c'è anche molto altro, come ho scoperto nel libro La scienza nascosta nei luoghi di Padova, presentata come "geografia scientifica urbana" da Telmo Pievani.

* Galileo Galilei si è trovato così bene a Padova, che qualcuno ha deciso per lui che dal 2 agosto 1823 la sua quinta vertebra lombare, donata dal medico vicentino Domenico Thiene, venisse conservata proprio a Palazzo Bo.

Fotografie realizzate durante la visita di istruzione a Padova, il 3 aprile 2024, con la classe 2AS.

Verifica di matematica, classe seconda liceo scientifico
Argomento: problemi risolvibili algebricamente, equazioni di secondo grado parametriche

Durata: 120 minuti

Verifica di matematica, classe seconda liceo scientifico
Argomento: problemi risolvibili algebricamente, equazioni di secondo grado parametriche

Durata: 120 minuti

Ho pochi ricordi del mio rapporto con la matematica alla scuola primaria, forse perché mi veniva facile e naturale, ma mi è rimasto impresso il disegno alla lavagna di un trapezio e la sua trasformazione in un triangolo equivalente, a spiegare perché per calcolare l’area fosse necessario sommare le basi e moltiplicarle per metà altezza. Forse in quel momento mi sono innamorata della geometria.

I ricordi più vividi sono quelli della scuola media: ricordo quando il professore assegnava delle espressioni da svolgere e le proponeva come sfida alla classe, tanto che in quei momenti, quando capitava che due persone si alzassero nello stesso momento, si assisteva a vere e proprie gare di corsa per raggiungere prima la cattedra. Ricordo, in particolare, che a volte arrivavi alla cattedra, soddisfatto del tuo lavoro e trepidante, ma il professore scuoteva la testa guardando il risultato e allora tornavi al tuo banco per riprovare, intestardendoti alla ricerca della strada corretta.

Del percorso liceale ricordo che l’errore in matematica ha cominciato a presentarsi con una maggiore frequenza, se penso ai problemi di geometria euclidea e analitica o di trigonometria, magari con tanto di discussione e sistemi parametrici al seguito. Capitava di intestardirsi su un problema che non dava il risultato corretto: al mattino, condividevo la mia frustrazione con mia cugina, che era in una classe parallela alla mia, e mi confrontavo con lei, che magari stava litigando con lo stesso problema (avevamo lo stesso insegnante) e ne parlavamo, ripercorrendo insieme le fasi della soluzione, mentre camminavamo verso la scuola. A volte succedeva che trovassimo la soluzione prima di arrivare in aula, e trascrivere i passaggi sul quaderno era solo la conferma di quanto avevamo già capito lungo il cammino. Altre volte, ancora, mi capitava di continuare a pensare al problema durante tutto il pomeriggio, senza riuscire a trovare una soluzione, ma al mattino mi svegliavo con la consapevolezza di conoscere quella soluzione e, prendendo in mano carta e penna, verificavo i passaggi, prima ancora di essere completamente sveglia: è stato in quel momento che ho capito l’importanza del “dormirci su”. Ancora adesso, con maggiore consapevolezza, se ho un problema che non riesco a risolvere (che sia di matematica o di altro) ci penso un attimo prima di addormentarmi, perché la mia testa possa continuare a lavorarci mentre riposo. È la stessa strategia che suggerisco ai miei alunni (per quanto, durante una verifica sia un po’ più difficile riuscire a “dormirci su”…). Mi fa ripensare a Poincaré che, dopo essersi concentrato a lungo e inutilmente su un problema, decise di partire per un gita e, mettendo piede sull’omnibus di Coutances, riuscì a trovare la soluzione (secondo il racconto fatto nel libro Le ostinazioni di un matematico, che racconta l’originale storia di Armand Duplessis, che avrebbe sprecato la propria vita nel tentativo di dimostrare la congettura di Goldbach).

Credo si sia colto il comune denominatore di questi tentativi: la testardaggine… e se penso al percorso universitario, questa mia caratteristica ha avuto un ennesimo banco di prova. Mi sono ritrovata nelle parole di Roberta Fulci che, durante la diretta con Ilaria Fanelli, Una matematica a Radio3 Scienza, ha risposto alla domanda di uno spettatore che chiedeva di essere rassicurato in merito alle sue difficoltà universitarie: Roberta ha raccontato che, avendo scelto matematica dopo il liceo classico, si è trovata ad affrontare grandi difficoltà durante il primo anno di corso ed ha avuto la sensazione di passare “dall’essere brava all’essere un rapa”. Come al solito, Roberta ha espresso il concetto in modo colorito e simpatico, come è tipico suo, e io ho capito perfettamente cosa intendesse, perché l’ho provato sulla mia pelle, anche se avrei dovuto essere più facilitata di lei, visto che alle spalle avevo un liceo scientifico! In realtà, arrivare alla fine del mio percorso universitario, alla tanto desiderata laurea in matematica, ha richiesto un bel po’ di caparbietà, tanto che a chi mi chiedeva che cosa avessi imparato dal mio percorso universitario rispondevo: “Ho imparato ad abbattere i muri a testate”.
Ho concluso il percorso universitario, nonostante… nonostante tutto! Per questo, forse, ho sempre ritenuto la caparbietà una componente fondamentale della buona riuscita in matematica. Addentrandomi sempre più nella storia della matematica, ho scoperto che essa è costruita sulla determinazione, sulla tenacia, sulla caparbietà. Uno dei primi libri che ho letto è L’ultimo Teorema di Fermat di Simon Singh: i tentativi di dimostrare il teorema si dipanano lungo i secoli, dando luogo a una staffetta espressione di un lavoro corale, come se ognuno dei matematici che ha preso parte a questo percorso avesse contribuito alla soluzione del puzzle apportando la propria piccola tessera, fino ad arrivare al risultato finale di Andrew Wiles. Per questo, forse, si parla di comunità matematica, pensando a quelle occasioni in cui i singoli matematici concentrano tutti le proprie forze per raggiungere un obiettivo comune, attraverso un lavoro continuo.

La mia convinzione che determinazione e caparbietà possano essere un’arma vincente anche a scuola mi ha portato a proporre, all’inizio di ogni percorso scolastico, una citazione di John Wooden, uno dei più grandi allenatori nella storia del basket delle università americane:

«Quando si migliora un po’ ogni giorno, alla fine si raggiungono grandi risultati. Quando si aumenta l’allenamento giorno dopo giorno, si ottiene un netto miglioramento della forma fisica. Non sarà domani, né dopodomani, ma poi i progressi saranno notevoli. È inutile puntare a grandi risultati in tempi brevi, conviene invece cercare di migliorare un po’, un giorno dopo l’altro. È l’unico modo per ottenere risultati duraturi.»

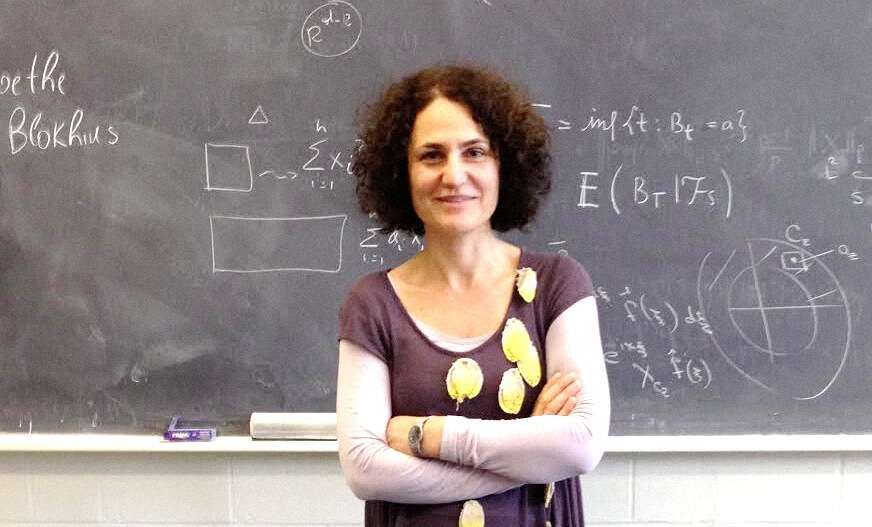
Gigliola Staffilani, prima donna italiana full professor al MIT, alla domanda rivoltale da Roberto Natalini in un’intervista del 2018 «Quanto del tuo lavoro è intuizione e quanto è solo duro lavoro?» ha dato una bella risposta: «Credo che l’intuizione arrivi quando ti sei chiarita abbastanza della tua mente da poterla ricevere. E per chiarirti devi lavorare duramente per cercare di eliminare tutti quei tentativi che non portano da nessuna parte.» Secondo la leggenda, pare che al re Tolomeo, che chiedeva un metodo rapido per studiare la geometria, Euclide abbia risposto che non esistono “vie regie”, ovvero percorsi privilegiati: in altre parole, ci sono stati matematici grandissimi nella storia, ma questo non significa che per loro le cose siano state più facili, perché avevano talento. Il duro lavoro resta una componente fondamentale per la buona riuscita in matematica!

Nei giorni scorsi, durante una lezione nella mia terza liceo scientifico, mentre le idee continuavano ad accumularsi intorno al tema della caparbietà, ho chiesto ai miei alunni quale potesse essere la caratteristica che una persona deve possedere per garantirsi un successo in matematica. Sono rimasta molto colpita dalle loro risposte: innanzi tutto perché molti di loro, invece di indicarmi una caratteristica, hanno risposto fornendo una strategia, che passava attraverso il ragionamento, la comprensione o la spesa di un po’ di tempo per creare collegamenti mentali, ma qualcuno ha risposto: «bisogna sapere le regole per poterle applicare meccanicamente» e, davanti alle mie proteste, si è difeso parlando di una strategia personale. Mi ha colpito, inoltre, che qualcuno ritenga importante il calcolo o “farsi piacere la matematica”, perché se è vero che, per certi aspetti, l’apprendimento è reso più facile dalla passione, non è certo possibile imporsi a comando di amare una disciplina. Dopo aver indicato la necessità di fare molti esercizi, qualcuno ha parlato di perseveranza e costanza, della capacità di non abbattersi per un risultato negativo, di forza di volontà e determinazione… e poi c’è il mio foglietto con scritto: caparbietà.

Ho voluto approfittare di queste risposte per riflettere con loro, a partire dalla storia di Sophie Germain (è mia intenzione partecipare a #peopleformath2024 lanciato dal canale IlariaF Math…). La sua vicenda biografica ha tutte le caratteristiche di un romanzo, con l’assunzione dell’identità di Antoine Le Blanc, per poter interloquire con i matematici più importanti dell’epoca come Lagrange e Gauss, e per approfondire la sua vita ho fatto riferimento al libro di Cecilia rossi Sophie Germain. Libertà, uguaglianza e matematica.

Al momento di costruire una bibliografia, mi sono imbattuta anche in Nothing stopped Sophie, di Cheryl Bardoe, con le illustrazioni di Barbara McClintock: si tratta di un libro per bambini, disponibile solo nella versione inglese, nel quale troviamo, ripetuto più volte, “Nothing stopped Sophie”, perché effettivamente niente riuscì a fermarla! Nel momento in cui i suoi genitori hanno cercato di ostacolarla nella sua passione per la matematica, lei ha trovato il modo di andare avanti, ad esempio.

Le donne che hanno scritto di lei considerano la caparbietà uno dei suoi lati più positivi, ma non è così se la sua vicenda viene interpretata da uomini: nel libro Il genio delle donne, Piergiorgio Odifreddi ha dedicato alla Germain il capitolo La prima vera matematica, ma non le risparmia il suo sarcasmo, visto che la definisce una giovane dal «carattere difficile e [dai] modi arroganti». Parlando poi del suo scontro con l’astronomo Joseph de Lalande, che l’aveva omaggiata del suo “Astronomia per le dame”, una delle pubblicazioni dell’epoca che trattava le donne con condiscendenza e proponendo una divulgazione in versione semplificata, dice che lei «disdegnava i testi divulgativi, e rivolse presto la sua attenzione alle difficili Disquisizioni aritmetiche», come se in realtà Sophie Germain peccasse di presunzione e non fosse realmente in grado di comprendere un testo del genere. Come insegnante ho imparato a considerare la presunzione e l’arroganza una necessità, per i giovani: senza presunzione, non potrebbero mettere in dubbio i tanti “ipse dixit” con i quali si trovano a confrontarsi quotidianamente, e senza un po’ di arroganza non avrebbero il coraggio di competere con gli adulti. Franco Pastrone, del Dipartimento di matematica dell’Università di Torino, nel suo intervento per l’Associazione Subalpina Mathesis, che è diventato l’introduzione nel libro di Maria Rosa Menzio Il Signor Le Blanc, ha un giudizio a tratti tranchant: riferendosi all’infanzia, parla di episodi «forse un po’ forzati al fine di esaltare la determinazione della ragazza», che descrive come una persona timida in pubblico, anche se, quando si trattava di ottenere dei risultati scientifici «la sua timidezza scompariva, anzi riusciva a mostrare una cocciuta aggressività».
Mi è parso quasi di cogliere che questa caparbietà, così positiva quando esercitata dagli uomini, diventasse un aspetto quasi negativo se declinato al femminile. Eppure, quando parliamo di Andrew Wiles, la sua determinazione viene celebrata, e la sua capacità di isolarsi dal resto del mondo per lavorare in autonomia alla dimostrazione non viene presa per presunzione, semmai gli viene riconosciuto il coraggio di aver rischiato tanto. Andrew Wiles ha avuto il coraggio di affrontare una sfida che aveva attraversato i secoli e, quando viene individuato un errore nella sua dimostrazione, prova a correggersi, impegnando altro tempo.

Non parla di presunzione, Gauss che, una volta conosciuta l’identità di Sophie Germain, le scrive:

«Il fascino di questa scienza sublime si rivela in tutta la sua bellezza solo a chi ha il coraggio di esplorarla. Una donna, a causa del suo sesso e dei nostri pregiudizi, incontra molti più ostacoli di un uomo nel familiarizzarsi con problemi complessi. Tuttavia, quando supera queste barriere e penetra nelle profondità più recondite, rivela di possedere il coraggio più nobile, un talento straordinario e un genio superiore.»

Per concludere, non può mancare un riferimento all’ultimo premio Abel, Michel Talagrand, che dichiara che «il segreto del successo in matematica è di lavorare ogni giorno fino a essere esausti ma non di più». Ne parlano, con dovizia di particolari, Beatrice Mautino ed Emanuele Menietti nel podcast del Post Ci vuole una scienza: Talagrand parla delle proprie difficoltà in matematica, legate a un “cervello lento” e a una “memoria terribile”, eppure dichiara di aver usato questo metodo proprio per superare le sue difficoltà. E direi che, visti i successi, non ci resta che fidarci!

Ricordo ora che anche Maryam Mirzakhani si è sempre definita una matematica lenta, ma è riuscita, nella sua breve vita, a raggiungere risultati eccezionali. Alex Eskin, dell’Università di Chicago, con il quale ha collaborato a lungo, racconta, nel film Secrets of the Surface, l’esperienza di lavoro con Maryam, paragonando il loro percorso a una camminata in montagna. Si trattava, come spesso succede, di una montagna inesplorata, e, a un certo punto, i due matematici hanno avuto l’impressione di poter raggiungere agevolmente la cima, quando un burrone ha sbarrato loro la strada. Con un sorriso dolce-amaro, Eskin racconta lo scoraggiamento che hanno provato, dato che quel burrone è costato loro due anni di duro lavoro e fatica. In tutto questo, Maryam si è mostrata positiva, anche se per un anno mezzo non ci fu nessun tipo di progresso. Per affrontare una fatica del genere e uscirne vittoriosi, è necessario avere una grande stabilità mentale e fiducia in sé stessi.

Aggiungendo queste caratteristiche alla caparbietà, credo proprio che il successo sia assicurato!